Классические примеры систем одновременных уравнений такие как кейнсианская модель формирования

Здесь мы рассмотрим классические примеры систем уравнений, которые подробно изучаются в стандартных экономических курсах.

1. Кейнсианская модель формирования доходов:

где К, С, / соответственно представляют собой совокупный выпуск, объем потреблений и инвестиций. Здесь / рассматривается как экзогенная переменная, а У — как эндогенная. Хорошо известно, что такая модель описывает закрытую экономику без государственного вмешательства.

Модель содержит одно поведенческое уравнение (9.28) и одно тождество (9.29).

Очевидно, модель (9.28)—(9.29) является идентифицируемой. Ее приведенная форма имеет вид:

2. Модель формирования спроса и предложения.

В простейшем виде эта модель рассматривалась в § 9.1. Здесь мы рассмотрим некоторые ее модификации.

Учет тренда. Если предположить, что привычки медленно меняются со временем, то в уравнение формирования спроса следует добавить временной тренд. Тогда модель будет иметь вид:

Приведенная форма записывается в виде:

откуда следует, что система не является идентифицируемой. В то же время параметр рз оказывается сверхидентифицируемым. В самом деле, записав уравнения регрессии в виде

легко заметить, что — и — дают оценку Р5.

Учет налога. Предположим теперь, что продавцы товара облагаются специальным налогом Т. Величина налога меняется со временем и в выборке представлена временным рядом, т. е. является экзогенной переменной. Тогда уравнение спроса не меняется (спрос определяется лишь одной эндогенной переменной — рыночной ценой товара), а в уравнение предложения добавляется соответствующий член. Тогда модель примет вид:

Очевидно, в этом случае модель будет идентифицируемой. Предположим теперь, что доход / считается постоянным на протяжении длительного времени. Тогда в уравнении спроса следует исключить переменную /, и получатся уравнения:

Система (9.33)—(9.34), очевидно, не является идентифицируемой. К ней может быть применен метод инструментальных переменных. При этом одна экзогенная переменная Г, рассматриваемая как инструментальная, позволяет, вообще говоря, идентифицировать только уравнение (9.33), в которое она не входит. Для идентификации (9.34) требуется «внешняя» инструментальная переменная.

Другим способом получить идентифицируемое уравнение формирования предложения оказывается ограничение на структурные коэффициенты: Ps= — р. Смысл этого ограничения очевиден: мы считаем, что продавцы исходят из суммы, которую они получают после уплаты налога, т.е. Р*=Р

Т. Тогда система может быть переписана в виде:

и экзогенная переменная Т может быть использована как инструментальная для идентификации обоих уравнений.

Видео:Макроэкономика. Основные модели макроэкономического равновесия.Скачать

Упражнения

9.1. Рассматривается система уравнений вида

Проверить, является ли данная система идентифицируемой. Изменится ли ответ, если в число регрессоров второго уравнения включить: а) константу; 6) переменную X ?

9.2. К системе двух уравнений вида

применен косвенный метод наименьших квадратов. Для коэффициентов приведенной формы

получены следующие оценки с= 2,2, С2=0,4, сз=0,08, С4=-0,5.

Найти оценки двухшагового метода наименьших квадратов, примененного к системе (9.35).

9.3. При оценивании системы (9.35) двухшаговым и трехшаговым методом наименьших квадратов получены одинаковые оценки. Будут ли оценки, полученные обычным методом наименьших квадратов, состоятельными?

Видео:Кейнсианская экономикаСкачать

Классические примеры систем одновременных уравнений такие как кейнсианская модель формирования

1. Кейнсианская модель формирования доходов.

Ct = α + βYt + εt
Yt = Ct + I t
где Y- совокупный выпуск
C — объем потреблений
I — объем инвестиций.
Здесь I рассматривается как экзогенная переменная, а Y – как эндогенная.
Такая модель описывает закрытую экономику без государственного вмешательства
Модель содержит одно поведенческое уравнение и одно тождество.

2. Модель формирования спроса и предложения.

Qd = β1 + β2P + β3I + ε1
Qs = β4 + β5P + ε2

Qd– спрос на товар
Qs– предложение товара
P – цена товара
I– цена товара
Если предположить, что рынок находится в состоянии равновесия, то в данных равенствах следует положить Qd = Qs = Q. В этом случае наблюдаемое значение P – это цена равновесия, которая формируется одновременно со спросом и предложением. Таким образом, мы должны считать P и Q объясняемыми переменными, а величину дохода I – объясняющей переменной.
Разделение ролей между переменными в системе одновременных уравнений может быть проинтерпретировано следующим образом:
переменные P и Q формируют свои значения, подчиняясь уравнениям, т.е. внутри модели. Такие переменные называют эндогенными.
переменная I считается в уравнениях заданной, ее значения формируются вне модели. Такие переменные называются экзогенными.
С математической точки зрения, главное отличие между экзогенными и эндогенными переменными заключается в том, что экзогенные переменные не коррелируют с ошибками регрессии, в то время как эндогенные могут коррелировать. Естественно предположить, что схожие случайные факторы действуют как на цену равновесия, так и на спрос на товар. Причинная зависимость между переменными и приводит, очевидно, к коррелированности их со случайными членами.
Набор экзогенных переменных может быть различным. Так, например, в модели спроса и предложения в качестве экзогенных переменных к доходу могут быть добавлены процентная ставка, временной тренд и т.д.
Рассмотрим модификации модели.
Учет тренда. Если предположить, что привычки медленно меняются со временем, то в уравнение формирования спроса следует добавить временной тренд. Тогда модель будет иметь вид:

Qd = β1 + β2P + β3I + ρt+ ε1
Qs = β4 + β5P + ε2

Учет налога. Предположим теперь, что продавцы товара облагаются специальным налогом Т. Величина налога меняется со временем и в выборке представлена временным рядом, т.е. является экзогенной переменной. Тогда уравнение спроса не меняется (спрос определяется лишь одной эндогенной переменной – рыночной ценой товара), а в уравнение предложения добавляется соответствующий член.
Тогда модель примет вид:
Qd = β1 + β2P + β3I + ε1
Qs = β4 + β5P + ρТ + ε2

Предположим теперь, что доход I считается постоянным на протяжении длительного времени. Тогда в уравнении спроса следует исключить переменную I , и получатся уравнения:
Qd = β1 + β2P + ε1
Qs = β4 + β5P + ρТ + ε2

Видео:Мультипликатор Кейнса - просто о сложномСкачать

Эконометрика, её задача и метод. Эконометрические модели и два принципа их спецификации (стр. 20 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

Теперь мы можем определить параметры последнего авторегрессионного уравнения и легко перейти к исходной модели. По найденному в результате регрессионного анализа коэффициенту отыскивается коэффициент , по коэффициенту при отыскивается коэффициент b, а по свободному члену отыскивается свободный член исходного уравнения a.

Различие между начальным и последним уравнениями состоит в том, что первая модель включает в себя ожидаемое значение фактора и к ней нельзя применять классические статистические методы. Последняя же модель включает в себя только фактические, то есть наблюдаемые значения переменных и ее параметры можно определить.

Однако, как и в случае с моделью Койка, применение классического МНК приведет к смещению оценок параметров ввиду наличия в правой части лагового значения результативного признака

38. Эконометрические модели из одновременных уравнений. Необходимое условие идентифицируемости уравнения модели (на примере простой кейнсианской модели формирования доходов).

Система взаимозависимых уравнений получила названиесистема совместных, одновременных уравнений. Тем самым под­черкивается, что в системе одни и те же переменныеуодновременно рассматриваются как зависимые в одних уравнениях и как независимые в других. В эконометрике эта система уравнений называется такжеструктурной формой модели.

Рассмотрев, как формируются основные компоненты совокупных расходов – потребительский спрос и инвестиционные расходы, – легко построить кейнсианскую функцию совокупного спроса. Она определяется как сумма планируемых домашними хозяйствами и фирмами расходов на товары, услуги и факторы производства для каждого из уровней совокупного дохода страны.

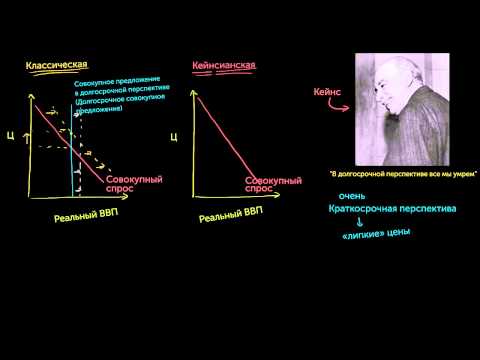
Данное определение существенно отличается от того, которое было дано при рассмотрении модели AD-AS. Там совокупный спрос был представлен в виде кривой, показывающей, какой объем национального производства домашние хозяйства и фирмы готовы купить при различных уровнях цен. Такая трактовка базируется на классическом понимании экономики, в которой господствует гибкое ценообразование и уровень цен может принимать любые значения.

Кейнсианская же модель описывает экономику в краткосрочном периоде, для которого характерны жесткие цены, и поэтому здесь совокупный спрос интерпретируется по-иному. Из сказанного следует, что при описании механизма взаимодействия спроса и предложения в кейнсианской модели традиционный график AD-AS, в котором по вертикальной оси откладывался уровень цен, а по горизонтальной – объем национального производства, использоваться не может.

Жесткость цен в экономике означает, что уравновешивание спроса и предложения происходит не за счет изменения уровня цен, а за счет того, что объемы продаж и изменение величины запасов дают фирмам информацию о том, что и сколько хотят иметь покупатели. Модель AD-AS, таким образом, может только обозначить равновесный объем производства, но не может показать, как это равновесие достигается.

Поэтому для описания равновесия в экономике с жесткими ценами придется построить график, отражающий зависимость величины спроса и предложения от объема национального дохода. Такой график носит название«кейнсианский крест» и представляет собой интерпретацию модели совокупного спроса−совокупного предложения в условиях жесткого ценообразования. На рис. 11.14 по горизонтальной оси отражается национальный доход Y, совпадающий по величине с объемом национального выпуска, а по вертикальной – объем совокупного спроса.

Рис. 11.14. Определение равновесного объема выпуска

Поскольку совокупный спрос равняется сумме спроса на потребительские и инвестиционные товары, то в графическом изображении он может быть представлен суммированием графиков потребления и инвестиций при каждом уровне дохода.

Совокупное предложение на графике отразить значительно проще: объем национального дохода равен величине национального продукта, который, в свою очередь, составляет весь объем предложения в экономике. Это значит, что кривая совокупного предложения начинается с нуля и направлена по прямой вверх под углом 45°, т. е. по биссектрисе. Следовательно, если национальный доход равен 1000 единиц, то и совокупное предложение должно быть равно 1000 единиц.

Если совместить обе кривые на одном графике, то можно найти точку, в которой объем совокупного спроса равен объему совокупного предложения. На рис. 11.14 равновесный выпуск представлен точкой Е, в которой уровень доходов равен совокупным расходам. В этой точке национальный выпуск составляет 1000 единиц, что соответствует такому же уровню доходов. В свою очередь, при уровне доходов 1000 единиц спрос на товары и услуги также составляет 1000 единиц, о чем свидетельствует линия AD, представляющая на графике пока лишь потребительские расходы С.

Таким образом, в точке Е количество предлагаемых товаров равно величине спроса на них при существующем уровне цен. Данная точка характеризует равновесие в кейнсианской модели, под которым понимается такое состояние в экономике, когда в ней отсутствуют тенденции к дальнейшим изменениям.

Это значит, что национальная экономика будет находиться в равновесии только в том случае, если совокупный спрос будет равен произведенному национальному доходу (совокупному предложению). При любом другом уровне выпуска, отличном от 1000, объем производства не совпадает с величиной совокупного спроса.

Например, если объем производства составит 500 единиц, то величина совокупного спроса будет превосходить этот объем, т. е. будет наблюдаться избыток совокупного спроса (AD > AS).

Подобная картина будет характерна для любого уровня выпуска ниже 1000 единиц. В данном случае будет наблюдаться явление, которому Дж. Кейнс дал название разрыв инфляции.

Слово «разрыв» в этом термине означает, что если фактический объем производства не совпадает с равновесным объемом, то в такой экономике образуется разрыв между спросом и предложением.

Иная картина будет наблюдаться, если фактический объем производства окажется выше равновесного. В этом случае в экономике будет иметь место избыток предложения товаров и услуг над совокупным спросом (AS>AD). В частности, при выпуске 1500 единиц совокупный спрос составит 1250 единиц. Данное явление Дж. Кейнс назвал разрывом безработицы.

Как экономика приходит к состоянию равновесия в случае его нарушения? В классической модели таким инструментом является механизм гибких цен. В кейнсианской модели объем производства управляетсяспросом.

В случае превышения совокупного спроса над совокупным предложением (AD>AS) фирмы увеличат занятость и уровень производства до существующего уровня спроса. В обратной ситуации (когда AS>AD) произойдет сокращение объемов выпуска продукции до уровня имеющегося совокупного спроса.

Таким образом, анализ «кейнсианского креста» показывает, что общее равновесие в экономике, устанавливаемое описанным способом, вовсе не обязательно соответствует такому уровню национального дохода, который позволяет обеспечить полную занятость. Равновесный объем национального дохода в кейнсианской модели определяется склонностью людей к потреблению, сбережению и инвестированию.

При низкой склонности к потреблению и инвестированию равновесный объем производства может оказаться ниже потенциального (достигаемого при полном использовании ресурсов). Беда такого состояния в том, что у экономики нет каких-либо движущих сил, способных вывести ее на уровень полной занятости. В частности, у фирм нет никаких стимулов загружать простаивающие производственные мощности и нанимать безработных, чтобы расширить производство, поскольку они будут не в состоянии продать произведенный объем продукции. При жестком уровне цен расширение выпуска будет упираться в дефицит совокупного спроса.

Что произойдет с равновесным объемом выпуска, если величина совокупного спроса возрастет? Предположим, что предприниматели оптимистично оценивают свое будущее и решают расширить производство за счет новых капиталовложений.

В этом случае совокупный спрос AD’ будет представлен уже не только потребительскими расходами С, но и инвестициями I, в результате чего получим модель, изображенную на рис. 11.15.

Рис. 11.15. Рост инвестиций приводит к увеличению объема выпуска

Мы видим, что увеличение инвестиций сдвигает кривую совокупного спроса вверх – с AD до AD’. Сдвиг кривой совокупного спроса приводит к увеличению объема выпуска, по мере того как экономика движется из точки Е в точку Е’. Это приводит, в свою очередь, к росту уровня доходов, при котором устанавливается новое равновесие.

Таким образом, суть кейнсианского анализа состоит в том, что экономика, предоставленная сама себе и функционирующая по принципу невидимой руки, весьма вероятно, может попасть в ситуацию либо инфляции, либо безработицы. Оказавшись в таком положении, она не в состоянии своими силами выбраться из него, поскольку в хозяйственной системе с жесткими ценами отсутствует внутренний механизм, обеспечивающий автоматическое уравновешивание совокупного спроса и совокупного предложения на уровне полной занятости.

Во времена классиков такой механизм существовал, это была система гибких цен, прежде всего гибкой заработной платы. Если в экономике возникала безработица, заработная плата понижалась и спрос на труд повышался до тех пор, пока все желающие работать не находили себе соответствующие рабочие места. Однако к 1930-м гг. на рынке труда существенно возросли роль и влияние профсоюзов, которые сумели значительно ограничить возможности предпринимателей в понижении цены труда. Поэтому экономика этого периода, придя в состояние равновесия при неполной занятости, может находиться в нем сколь угодно долго, не обнаруживая ни малейшей тенденции вовлечь в производство неиспользованные ресурсы, в первую очередь, свободную рабочую силу.

Видео:Модель AD-AS, совокупный спрос, совокупное предложение, шоки, равновесиеСкачать

Системы эконометрических уравнений

При изучении сложных социально-экономических систем измерение тесноты связей между переменными, построение изолированных уравнений регрессии недостаточны для описания таких систем и объяснения механизма их функционирования. При использовании отдельных уравнений регрессии, например, для экономических расчетов в большинстве случаев предполагается, что факторы можно изменять независимо друг от друга. Однако это предположение является очень грубым: практически изменение одной переменной, как правило, не может происходить при абсолютной неизменности других. Ее изменение повлечет за собой изменения во всей системе взаимосвязанных признаков. Следовательно, отдельно взятое уравнение множественной регрессии не может характеризовать истинные влияния отдельных признаков на вариацию результирующей переменной. Именно поэтому в экономических, биометрических и социологических исследованиях важное место заняла проблема описания структуры связей между переменными системой одновременных уравнений или структурных уравнений. Например, если изучается модель спроса как соотношение цен и количества потребляемых товаров, то одновременно для прогнозирования спроса необходима модель предложения товаров, в которой рассматривается также взаимосвязь между количеством и ценой предлагаемых благ. Это позволяет достичь равновесия между спросом и предложением. При оценке эффективности производства нельзя руководствоваться только моделью рентабельности. Она должна быть дополнена моделью производительности труда, а также моделью себестоимости единицы продукции.

В еще большей степени возрастает потребность в использовании системы взаимосвязанных уравнений, если мы переходим от исследований на микроуровне к макроэкономическим расчетам. Модель национальной экономики включает в себя следующую систему уравнений: функции потребления, инвестиций, заработной платы, тождество доходов и т.д. Это связано с тем, что макроэкономические показатели, являясь обобщающими показателями состояния экономики, чаще всего взаимозависимы. Так, расходы на конечное потребление в экономике зависят от валового национального дохода. Вместе с тем величина валового национального дохода рассматривается как функция инвестиций. Система уравнений в эконометрических исследованиях может быть построена по-разному. Возможна система независимых уравнений, когда каждая зависимая переменная у рассматривается как функция одного и того же набора факторов :

Набор факторов х, в каждом уравнении может варьировать. Модель вида

также является системой независимых уравнений, но набор факторов в ней видоизменяется в уравнениях, входящих в систему. Отсутствие того или иного фактора в уравнении системы, может быть следствием как экономической нецелесообразности его включения в модель, так и несущественности его воздействия на результативный признак (незначимо значение t-критерия или частного F-критерия для данного фактора).

Каждое уравнение системы независимых уравнений может рассматриваться самостоятельно. Для нахождения его параметров используется метод наименьших квадратов. По существу, каждое уравнение этой системы является уравнением регрессии. Поскольку никогда нет уверенности, что факторы полностью объясняют зависимые переменные, в уравнениях присутствует свободный член . Так как фактические значения зависимой переменной отличаются от теоретических на величину случайной ошибки, в каждом уравнении присутствует величина случайной ошибки ().

Если зависимая переменная одного уравнения выступает в виде фактора в другом уравнении, то модель может быть построена в виде системы рекурсивных уравнений. Примером такой системы может служить модель производительности труда и фондоотдачи:

где — производительность труда, — фондоотдача, — фондовооруженность труда, — энерговооруженность труда, — квалификация рабочих.

Каждое уравнение модели производительности труда и фондоотдачи может рассматриваться самостоятельно, и его параметры определяются методом наименьших квадратов.

Наибольшее распространение в эконометрических исследованиях получила система взаимозависимых уравнений. В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях — в правую часть системы:

Система взаимозависимых уравнений получила название система совместных, одновременных уравнений. Тем самым подчеркивается, что в системе одни и те же переменные одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других. В эконометрике эта система уравнений называется также структурной формой модели. В отличие от предыдущих систем каждое уравнение системы одновременных уравнений не может рассматриваться самостоятельно, и для нахождения его параметров традиционный МНК не применим. С этой целью используются специальные приемы оценивания.

Примером системы одновременных уравнений может служить модель динамики цены и заработной платы:

где — темп изменения месячной заработной платы; — темп изменения цен; — процент безработных; — темп изменения постоянного капитала; — темп изменения цен на импорт сырья.

Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции принятой модели. Экономические переменные могут выступать в одних моделях как эндогенные, а в других — как экзогенные переменные. Внеэкономические переменные (например, климатические условия) входят в систему как экзогенные переменные. В качестве экзогенных переменных могут рассматриваться значения эндогенных переменных за предшествующий период времени (лаговые переменные). Так, потребление текущего года может зависеть не только от ряда экономических факторов, но и от уровня потребления в предыдущем году .

Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Целесообразно в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регулирования. Меняя их и управляя ими, можно заранее иметь целевые значения эндогенных переменных. Структурная форма модели в правой части содержит коэффициенты при эндогенных переменных, — при экзогенных переменных, которые называются структурными коэффициентами модели. Все переменные в модели выражены в отклонениях от среднего уровня, т.е. под подразумевается (), а под — соответственно (). Поэтому свободный член в каждом уравнении системы отсутствует. Использование МНК для оценивания структурных коэффициентов модели дает, как принято считать в теории, смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма модели преобразуется в приведенную форму модели.

Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:

где — коэффициенты приведенной формы модели.

По виду приведенная форма модели ничем не отличается от системы независимых уравнений, параметры которой оцениваются традиционным методом наименьших квадратов. Применяя МНК, можно оценить , а затем оценить значения эндогенных переменных через экзогенные.

Эконометрические модели обычно включают в систему не только уравнения, отражающие взаимосвязи между отдельными переменными, но и выражения тенденции развития явления, а также разного рода тождества. Например, Т. Хаавелмо, исследуя линейную зависимость потребления () от дохода (), предложил одновременно учитывать тождество дохода. В этом случае модель имеет вид:

где и — параметры линейной зависимости от ; — инвестиции в основной капитал и в запасы экспорта и импорта.

Оценки параметров должны учитывать тождество дохода в отличие от параметров обычной линейной регрессии. В этой модели две эндогенные переменные — и , и одна экзогенная переменная . Система приведенных уравнений составит:

Она позволяет получить значения эндогенной переменной через переменную . Рассчитав коэффициенты приведенной формы модели (), можно перейти к коэффициентам структурной модели и , подставив в первое уравнение приведенной формы выражение переменной из второго уравнения приведенной формы модели. Приведенная форма модели хотя и позволяет получить значения эндогенной переменной через значения экзогенных переменных, аналитически уступает структурной форме модели, так как в ней отсутствуют оценки взаимосвязи между эндогенными переменными.

При переходе от приведенной формы модели к структурной исследователь сталкивается с проблемой идентификации. Идентификация — это единственность соответствия между приведенной и структурной формами модели.

С позиции идентифицируемости структурные модели можно подразделить на три вида: 1) идентифицируемые; 2) неидентифицируемые; 3) сверхидентифицируемые.

Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т.е. если число параметров структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты модели оцениваются через параметры приведенной формы модели и модель идентифицируема. Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели. Структурная модель в полном виде, содержащая эндогенных и предопределенных переменных в каждом уравнении системы, всегда неидентифицируема. Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. В этой модели число структурных коэффициентов меньше числа коэффициентов приведенной формы.

Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых необходимо проверять на идентификацию. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение. Выполнение условия идентифицируемости модели проверяется для каждого уравнения системы. Для того, чтобы уравнение было идентифицируемо, нужно, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного.

Если обозначить число эндогенных переменных в j -ом уравнении системы через , а число экзогенных (предопределенных) переменных, которые содержатся в системе, но не входят в данное уравнение, через , то условие идентифицируемости модели может быть записано в виде правила: — уравнение идентифицируемо, — уравнение неидентифицируемо, — уравнение сверхидентифицируемо.

В эконометрических моделях часто наряду с уравнениями, параметры которых должны быть статистически оценены, используются балансовые тождества переменных, коэффициенты при которых равны . В этом случае, хотя само тождество и не требует проверки на идентификацию, поскольку коэффициенты при переменных в тождестве известны, в проверке на идентификацию собственно структурных уравнений системы тождества участвуют.

Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение получили следующие методы оценивания коэффициентов структурной модели: 1) косвенный метод наименьших квадратов (КМНК); 2) двухшаговый метод наименьших квадратов (ДМНК); 3) трехшаговый метод наименьших квадратов (ТМНК); 4) метод максимального правдоподобия с полной информацией (ММПѓ); 5) метод максимального правдоподобия при ограниченной информации (ММПs).

Косвенный метод наименьших квадратов используется в случае точно идентифицируемой структурной модели. Процедура применения КМНК предполагает выполнение следующих этапов работы:

• * структурная модель преобразовывается в приведенную форму модели;
• * для каждого уравнения приведенной формы модели обычным МНК оцениваются приведенные коэффициенты ();
• * коэффициенты приведенной формы модели трансформируются в параметры структурной модели.

Если система сверхидентифицируема, то КМНК не используется, ибо он не дает однозначных оценок для параметров структурной модели. В этом случае могут применяться разные методы оценивания, среди которых наиболее распространенным и простым является двухшаговый метод наименьших квадратов. Основная идея ДМНК — на основе приведенной формы модели получить для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения. Далее, подставив их вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения. Метод получил название «двухшаговый метод наименьших квадратов», ибо МНК используется дважды: на первом шаге при определении приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенной переменной и на втором шаге применительно к структурному сверхидентифицируемому уравнению при определении структурных коэффициентов модели по данным теоретических (расчетных) значений эндогенных переменных. Сверхидентифицируемая структурная модель может быть двух типов: 1) все уравнения системы сверхидентифицируемы; 2) система содержит наряду со сверхидентифицируемыми точно идентифицируемые уравнения. Если все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений.

Метод максимального правдоподобия рассматривается как наиболее общий метод оценивания, результаты которого при нормальном распределении признаков совпадают с МНК. Однако при большом числе уравнений системы этот метод приводит к достаточно сложным вычислительным процедурам. Поэтому в качестве модификации используется метод максимального правдоподобия при ограниченной информации (метод наименьшего дисперсионного отношения), разработанный Т. Андерсоном и Н. Рубиным. В отличие от метода максимального правдоподобия в данном методе сняты ограничения на параметры, связанные с функционированием системы в целом. Это делает решение более простым, но трудоемкость вычислений остается достаточно высокой. Сейчас он практически вытеснен двухшаговым методом наименьших квадратов в связи с гораздо большей простотой последнего. Этому способствовала также разработка Г. Тейлом семейства оценок коэффициентов структурной модели. В последнем случае решение структурной модели соответствует оценкам по ДМНК.

Развитием двухшагового метода наименьших квадратов является трехшаговый МНК (ТМНК), предложенный А. Зельнером и Г. Тейлом. Этот метод оценивания пригоден для всех видов уравнений структурной модели. Однако при некоторых ограничениях на параметры более эффективным оказывается ДМНК.

Экономически значимыми примерами систем одновременных уравнений являются:

1. Кейнсианская модель формирования доходов:

где , — соответственно представляют собой совокупный выпуск, объем потребления и инвестиций. Здесь рассматривается как экзогенная переменная, а — как эндогенная. Такая модель описывает закрытую экономику без государственного вмешательства. Модель содержит одно поведенческое уравнение и одно тождество.

Очевидно, модель является идентифицируемой. Ее приведенная форма имеет вид:

Известна более поздняя модификация статистической модели Кейнса, включающая функцию сбережений:

Модель содержит три эндогенные переменные — и одну экзогенную переменную — . Система идентифицируема: в первом уравнении и , во втором и . — предопределенная переменная.

2. Динамическая конъюнктурная модель Клейна:

где — функция потребления в период ; — заработная плата в период ; — прибыль в период ; — прибыль в период ; — общий доход в период ; — общий доход в период ; — время; — чистые трансферты в пользу администрации в период ; — капиталовложения в период ; — спрос административного аппарата, правительственные расходы в период времени .

3. Модель формирования спроса и предложения, состоящая из трех уравнений (двух поведенческих и одного тождества):

где — предлагаемое количество благ (объем предложения),

— спрашиваемое количество благ (объем спроса),

В этой системе 3 эндогенные переменные — . При этом, если переменные представляют собой эндогенные переменные исходя из структуры самой системы (они расположены в левой части), то является эндогенной переменной по экономическому содержанию (цена зависит от предлагаемого и спрашиваемого количества благ), а также в результате наличия тождества .

Рассматриваемая модель спроса и предложения не содержит экзогенной переменной. Для того, чтобы модель имела статистическое решение и можно было убедиться в ее справедливости, в модель вводятся экзогенные переменные. Одним из вариантов модели спроса и предложения является модель вида:

где — доход на душу населения,

— климатические условия (или другие факторы внешней среды).

Переменные и — экзогенные, введя их в модель, получим идентифицируемую структурную модель, оценки параметров которой могут быть даны с помощью КМНК.

Как уже отмечалось, не все эконометрические модели имеют вид системы одновременных уравнений. Так, широкий класс функций спроса на ряд потребительских товаров часто представляет собой рекурсивную систему, в которой с уравнениями можно работать последовательно и проблемы одновременного оценивания не возникают. В этом плане система одновременных уравнений — лишь один из возможных вариантов построения экономических моделей.

🎬 Видео

Экономические учения: Кейнсианство и его основы. Почему это не идеальная модель экономики?! История!Скачать

Решение систем уравнений методом подстановкиСкачать

Макроэкономика-Кейнсианская модель макроэкономического равновесия на товарном рынке «доходы-расходы»Скачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Кейнсианский крестСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Модель IS-LM и революция КейнсаСкачать

Механизм формирования равновесия в экономике в модели AD/AS (теория)Скачать

Модели экономического роста (часть 1)Скачать

Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

Графический способ решения систем уравнений. Алгебра, 9 классСкачать

История экономической мысли (Марксизм, Кейнсианство)Скачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

Макроэкономический анализ и прогноз с использованием модели Кейнса (теория) (часть 2)Скачать

Пестунова Г. лекция № 3 "Макроэкономика"Скачать

9 класс, 10 урок, Основные понятия, связанные с системами уравнений и неравенств с двумя переменнымиСкачать