Физическая химия полимерных гелей Лекция 18 ВЛИЯНИЕ СВОЙСТВ КОНТАКТИРУЮЩИХ ФАЗ НА ОБЪЕМ ФАЗЫ ВР В ПГ. ЧАСТЬ 2
Физическая химия полимерных гелей Лекция 20 ГЕТЕРОФАЗНАЯ ФИЗИКО-МАТЕМАТИЧЕСКАЯ КИНЕТИЧЕСКАЯ МОДЕЛЬ НАБУХАНИЯ ПОЛИМЕРНЫХ ГЕЛЕЙ
Видео:Степень полимеризации. Решение задач. Ч.1.Скачать

Физическая химия полимерных гелей Лекция 19 РАЗВИТИЕ ПРЕДСТАВЛЕНИЙ О КИНЕТИКЕ НАБУХАНИЯ ПГ
Физическая химия полимерных гелей
Ферапонтов Н. Б., Гагарин А. Н., Струсовская Н. Л., Токмачёв М. Г., Тробов Х.Т., Рубин Ф.Ф.
Москва, МГУ имени М. В. Ломоносова 2015 г.
Растворению сухого полимера в воде и водных растворах предшествует его набухание – изменение массы и объема образца в результате поглощения компонентов из внешнего раствора [1]. В качестве количествен- ной характеристики этого явления используют степень набухания:
Таким образом a – это относительное приращение объема или массы образца. Различают два типа набухания: ограниченное и неограниченное. В первом случае между макромолекулами имеются сшивающие их поперечные связи. В этом случае набухание не завершается растворением, и степень набухания достигает со временем некоторого предельного значения.
Неограниченное набухание плавно переходит в растворение. В этом случае a сначала возрастает, а затем снижается до нуля. Часто допускают, что ограниченное набухание, контролируемое диффузией, описывается кинетическим уравнением реакции первого порядка. Согласно кинетическому уравнению реакции первого порядка, скорость набухания при любом данном времени t прямо пропорциональна текущей степени набухания [1,2].
где ? – набухание ко времени t; (?max–?) – нереализованное промежуточное набухание; k – коэффициент пропорциональности между скоростью набухания и нереализованной степенью набухания.
Отличие от реакций первого порядка состоит лишь в ином начальном условии: здесь полагают, что при t=0 ?=0, а при t>? ?>?max.Поэтому решение уравнения (3) в явной (экспоненциальной форме):
Константу скорости набухания наб k нетрудно найти, определив экспериментально предельное набухание, а также промежуточное набухание a на момент времени t.
Рис. 1. Графики зависимостей степени набухания от времени в линейной (логарифмической) и явной (экспоненциальной) формах.
Уравнение (4) описывает набухание различных полимеров в воде, их сжатие при высушивании, набухание растительного каучука разной степени вулканизации в различных жидкостях [2]. Однако наблюдаются отклонения от этого уравнения, особенно при больших временах и степенях набухания. В обычной практике уравнение первого порядка используют для исходного и иногда для промежуточного этапа процесса набухания. Наиболее высокие степени набухания, для которых отклонения от уравнения (4) слишком велики, чтобы их не учитывать, не включены в расчеты. Вывод уравнения (4) основан на законе Фика и относится к набуханию, контролируемому диффузией.
В работе [3] предложено описывать получаемые в эксперименте кинетические кривые, учитывая влияние на набухание исходного состояния полимера. Изучены два варианта набухания: при помещении сухого геля в воду и при переносе геля, набухшего в воде, в раствор соли. В первом случае кинетика набухания сначала изменяется пропорционально квадрату исходного размера геля, а при дальнейшем набухании изменяется линейно по сравнению с исходным размером геля. В работе указывается причина такого поведения геля: когда гель набухает из сухого состояния, он набухает через последовательное сосуществование различных фаз. Авторы работы [3] аппроксимировали кинетические кривые набухания геля функцией:
где r(t) – радиус набухшего в воде геля при равновесии; r0 – радиус исходной сухой частицы геля; r max – максимальный радиус геля; t – характеристическое время.
Показано, что набухание вначале может быть описано диффузионным подходом, но чем больше гель набухает, тем более важную роль играют электростатические взаимодействия, которые не подчиняются диффузионному механизму. Два механизма, очевидно, перекрываются в середине набухания.
Для диффузионного механизма характеристическое время ? пропорцио- нально квадрату исходного размера r0:
где D – коэффициент диффузии.
Более низкая степенная зависимость отражает существование двух описанных механизмов. Таким образом, показано, что кинетика набухания полиэлектролитного геля в воде включает два различных механизма. В то время как перенос из сухого состояния в набухшее можно рассматривать, основываясь на существующих диффузионных моделях, дополнительное набухание, которое наблюдается, – это новое явление, которое еще не объяснено.
В работах [4,5] отмечается, что скорость набухания гидрогеля контролируется как диффузией молекул растворителя, так и релаксацией полимерной структуры, т.е. скорость набухания пропорциональна квадрату остаточной способности набухания (SRe—SR)2:
где SR – текущая степень набухания геля, SRe – равновесная степень набухания геля.
Проинтегрировав уравнение (8), авторы получили уравнение второго порядка – уравнениеШотта [5], в координатах которого строили кинетические кривые, выделяли на них линейные участки и определяли их наклоны:
где k – константа скорости.
Таким образом, было показано, что кинетика набухания геля в растворах солей хорошо описывается кинетическим уравнением второго порядка (9).
Кроме того, наблюдали скачкообразное набухание гидрогеля при перемещении его из растворов солей в воду и объясняли его осмотическим давлением, создаваемым противоионами [5].
Рис. 2. Сорбция триптофана на катионите КУ-2-8, первоначально находившегося в H- форме, из растворов с pH 2 (a) и при pH 1 (б).
Однако известны случаи, когда при набухании полимерных гелей, вместо обычной монотонной зависимости, наблюдались колебания [6].
Кинетические аномалии такого рода были получены не только на ионитах, но и на полимерах с недиссоциирующими полярными группами [7,8].
Причина такого поведения полимеров кроется в циклическом характере проникновения воды в полимерную матрицу. Такой режим набухания может быть связан с кинетикой ионного обмена, в результате которого изменяется состав раствора и, соответственно, активность воды, с различной вязкостью внешнего раствора и раствора внутри геля, а также с другими похожими причинами. Математическое описание такого рода процессов впервые было предложено в работе [7]. Было показано, что возникновение колебаний можно объяснить теоретически, если предположить периодическое неоднородное строение поверхности полимера и учесть кинетику образования поверхностного слоя молекулярно сорбированной аминокислоты.
Проведенное моделирование показало, что в принципе кинетические кривые сорбции могут иметь немонотонный колебательный характер. Это объясняется взаимным влиянием ионного обмена, молекулярной сорбции и встречной диффузии, создающим положительную обратную связь при колебаниях концентрации. Слабой стороной данного объяснения являются дополнительные требования к строению полимера.
В работе [9] показано, что колебания, возникающие при сорбции аминокислот, могут быть просто объяснены, если учесть изменение объема геля при изменении в нем концентрации внутреннего раствора. Дано теоретическое объяснение явления и приведены результаты математического моделирования, позволяющие проанализировать правомерность объяснения.
Перечислены факторы, способные увеличивать величину объема внутреннего раствора с ростом концентрации: аминокислота во внутреннем растворе может ослаблять связь между нитями сорбента, позволяя им раздвинуться.
Еще одним фактором является изменение осмотического давления при изменении концентрации. Если рассматривать поверхностный слой сорбента как полупроницаемую мембрану, через которую легко проходят молекулы воды, но значительно хуже большие молекулы аминокислоты с водными оболочками. В момент опускания гранул в раствор в нем концентрация аминокислоты равна C0, а во внутреннем растворе гранулы равна нулю, что порождает осмотическое давление. Под его воздействием часть воды покидает гранулу. Это состояние является начальным для процесса диффузии аминокислоты внутрь гранулы и ее сорбции. Последующее увеличение концентрации во внутреннем растворе приводит к уменьшению осмотического давления, и сорбент «распрямляется».
Таким образом, в работе показано, что в случае сорбции аминокислот в ионите удается достаточно простой моделью описать процесс и объяснить возникновение колебаний, установив положительную обратную связь между величинами потоков раствора и концентрациями компонентов.
Следует отметить, что до 1970 гг. кинетика полимерных процессов была изучена весьма слабо. Позже ее изучению способствовало как развитие компьютерной техники, так и возросший практический интерес. В 1973 году Танака [10] предложил свою теорию, согласно которой набухание полимера происходит в результате одновременного протекания двух процессов – диффузии вещества внутри гранулы и релаксации полимерной сетки под воздействием трения между полимерной сеткой и гелевой жидкостью.
Характерное время набухания пропорционально отношению площади к объему геля, а также коэффициенту диффузии жидкости в полимерной сетке, который определяется как отношение модуля продольного растяжения сетки к коэффициенту трения между сеткой и гелевой жидкостью. Здесь заложена существенная разница между данной теорией и теорией, существовавшей до этого, базировавшейся на предположении, что время набухания определяется коэффициентом диффузии молекул жидкости.
Эксперименты на 5% полиакриламидном геле показали хорошее совпадение с теорией, значение коэффициента диффузии, полученное из экспериментов по макроскопическому набуханию, хорошо согласуется с аналогичным коэффициентом, полученным с помощью спектроскопии рассеянного лазерного излучения.
В более поздней работе (1990 г) [11] авторы предложили механизм изменения объема полимера с учетом двух процессов, так как они считали, что изменение объема не есть чисто диффузионный процесс. Существенную роль при набухании играет модуль упругости (англ. shear modulus). Таким образом, важную роль играет геометрия геля. Исходя из аналитического решения уравнения диффузии дляшарообразного зерна Ли и Танака предположили, что изменение объема геля описывается бесконечной суммой экспонент с отрицательным показателем.
При этом, множители при экспонентах зависят только от качества набухающего агента (англ. swelling agent), а показатели экспонент относятся как квадраты натуральных чисел (a/1=b/4=c/9=…). В работе формулируется теорема флуктуации-диссипации. Приводятся выражения для описания кинетических процессов на полимерах произвольной формы. В статье даются явные аналитические решения для гелей в форме бесконечного цилиндра и большого диска. Расчеты показывают, что эффективные коэффициенты диффузии для гелей в форме длинного цилиндра и для большого диска в 1.5 и в 3 раза меньше, чем для гелей сферической формы, соответственно. Если брать диаметр цилиндра, диаметр шара и толщину диска одинаковыми, то времена релаксации для гелей с малым коэффициентом упругости меньше в 2.0 и в 5.7 раза соответственно. Теория также показывает, что экспериментально измеряемые скорости протекания процесса в длинном цилиндре и в диске вдоль оси z и вдоль радиальной оси – одинаковые.
Результаты хорошо согласуются с экспериментальными данными.
В статье приведены графики логарифма изменения объема гранулы от времени и показано, что они лежат на одной прямой, за исключением начального короткого (по времени) участка. По ним авторы стремились вычислять усредненные коэффициенты диффузии (пытаясь описывать протекание процесса кинетическим уравнением первого порядка).
Экспериментальные результаты показывают хорошее совпадение кинетических кривых расчетам по уравнению первого порядка на промежутке времени с 30 по 800 минуты. На начальном участке наблюдается отклонение от линейной зависимости. Подобные экспериментальные результаты отмечены и у других авторов. Следует отметить, что для идеальных сферических гранул модель считает только внутреннюю диффузию.
Скотт в 1986–1990 гг. [12] показал, что кинетики первого порядка недостаточно, даже для описания случаев, когда изменение объема мало.
Согласно его данным, при набухании полимера проходят два процесса – диффузии растворенного вещества внутрь зерна (быстрый процесс) и релаксация объема к равновесному состоянию под воздействием возникающих напряжений в деформированной полимерной сетке. В работе также отмечалось, что к 90-м годам было мало исследований кинетики набухания полимеров. Теоретические исследования, построенные на базе представлений о набухании под воздействием диффузии, показывали, что кинетики первого порядка не достаточно. Приводятся обширные данные по исследованию скорости набухания и равновесий закрепленных и незакрепленных пленок желатина. Диффузия там всегда быстрая. Когда она заканчивается, скорость набухания контролируется выравниванием напряжения в деформированной полимерной сетке. Кинетические уравнения для этого процесса, которые также применимы к регенерированной целлюлозе, как показано, представляют собой уравнения второго порядка по отношению к оставшейся емкости сорбента. Эти уравнения вида:
В статье предполагается, что скорость набухания зависит от двух факторов – доли незаполненного пространства (диффузионный процесс заполнения пустого пространства) и сопротивления, связанного с упругостью полимерной сетки. Второй фактор пропорционален внутренней специфической площади в зоне, включающей в себя все области, которые еще не прореагировали с водой, но которые только собираются стать гидратированными и набухнуть в будущем процессе. Т. о. автор объясняет возникновения квадратичного члена в кинетическом дифференциальном уравнении, которое совпадает с эмпирическим уравнением Робинсона.
В работе [13] Пэппас и Браннон–Пэппас рассматривали кинетику набухания полиметакриловой кислоты и сополимера полиакриловой кислоты с полигидроксиэтилметакрилатом. Они наблюдали зависимость кинетики набухания от рН раствора и от ионной силы в этих гелях. Авторами была разработана модель для описания кинетики набухания ионных форм гидрогелей в ответ на изменения ионной силы раствора.
Когда гель набухает при изменении рН, существует соответствующее изменение объема или длины полимерной цепи. Основываясь на набухании, деформация в геле, ?, может быть вычислена в любой момент времени набухания как:
где l – длина в любое время и l0 – начальная длина.
По принципу суперпозиции Больцмана деформация в зависимости от изменения pH или ионной силы раствора может быть вычислена как:
где – изменение pH или ионной силы, а – ионная механическая поправка, которая является функцией полимера.
Предполагая, что набухание в геле изотропно, соотношение объёмов при набухании геля может быть записано в виде:
где Vs(t) – объём набухшего геля в любой момент времени, а Vd – начальный объём сухого полимера. Комбинируя 11 и 12, набухание геля в зависимости от изменения pH или ионной силы раствора может быть описано как:
Авторы данной работы показали, что можно предсказать набухание как нейтральных, так и ионных форм гелей при различных условиях.
В работе [14] исследована кинетика набухания и сжатия дисков поливинилацетата, набухающих в изопропиловом спирте при различных температурах. При этом определялся общий коэффициент диффузии и отношение модуля упругости к продольному осмотическому давлению на базе теории Ли и Танаки. Авторы наблюдали хорошее соответствие между теоретическими и экспериментальными результатами макроскопического изменения объема.
В 1997 г. исследователи из северного Техаса предложили другой механизм релаксации объема полимерной гранулы к ее равновесному значению. В статье [15] с помощью математического моделирования анализируется кинетика набухания геля с учетом движения как раствора НМС, так и полимерной сетки. Эта модель не использует подход двух процессов от Ли и Танака, в котором движение раствора учитывается неявно.
Аналитическое решение для описания движения раствора и сетки находится из системы уравнений общей диффузии для объектов – бесконечный цилиндр и большой плоский диск. Для цилиндрического объекта скорость движения раствора пропорциональна радиусу в радиальном направлении и координате z вдоль оси симметрии цилиндра. Авторы получили, что процесс набухания в цилиндре и на диске идет медленнее, чем ожидается, основываясь на теории чисто внутренней диффузии. В этой статье авторы модифицировали и расширили подход Ли и Танаки, путем добавления учета движения как раствора, так и полимерной сетки.
В 2000 г. финские химики изучали процессы набухания полиуретанов (ПУ) различных типов [16]. Они показали, что только малая часть таких реакций может быть описана с помощью кинетических уравнений первого порядка. Кроме того, ими отмечено, что параметры процесса существенно зависят от температуры. Процесс обработки трех типов алифатических полиуретанов наблюдался посредством измерения изменений в сорбционных свойствах их изоцианатных групп. Два экспоненциальные подхода использовались для описания уменьшения связки между изоцианатными группами во времени. Исследуемый процесс включал в себя химический и диффузионный периоды. В соответствии с анализом кинетики сшитых полимеров, один из ПУ описывается кинетическим уравнением первого порядка, а два других – кинетическим уравнением второго порядка. Поведение набухания алифатических ПУ описывалось посредством нахождения доли геля и степени сшивки после обработки образца. Предложены уравнения типа:
В 2005 г. американские ученые из Массачусетса предложили оригинальный механизм изменения объема полимерной гранулы при ее набухании [17]. Сшитые полимерные сетки, безотносительно от метода сшивки, содержат доли неприсоединенных мономерных молекул. В процессе набухания в растворе НМС, эти отдельные макромолекулы участвуют как альтернативный раствор. Также, они покидают пределы полимера и выходят во внешний раствор, пока не будет достигнуто динамическое равновесие.
Таким образом, набухший полимер следует трактовать как сложную систему из собственно полимерной матрицу, раствора ВМС и раствора НМС. На базе теории Флори-Рейнера, была разработана первая модель для предсказания поведения таких систем при набухании. Переходные состояния трактуются как квазиравновесные, при этом оценивается конечное условие равновесия.
Также изучается эффект выхода полимерных молекул во внешний раствор. В статье оценены результаты набухания частично-сшитого высокоплотного полиэтилена в параксилоле. Приведены кинетические кривые с экстремумом.
Быстрый процесс – проникновение раствора НМС в гранулу полимера и резкое набухание. Медленный процесс – выход отдельных несвязанных макромолекул во внешний раствор и релаксация объема полимера к равновесному значению.
В работах [18, 19] авторы изучали параметры, влияющие на кинетику набухания гидрофильных полимеров, и выяснили, что она зависит от нескольких физико-химических факторов, в частности, размер частиц, пористость и тип пористой структуры. Осмотические силы давления, электростатические силы и вязкоэластичные силы являются тремя основными параметрами, регулирующими набухание гидрогелей. Для описания влияния этих различных сил надлежащим образом, моделирование проводится на разных уровнях, основанных на глобальных от макроскопических до микроскопических теорий. Теоретическое описание набухания гидрогелей основывается на минимизации свободной энергии Гиббса геля. Кинетические модели были разработаны, чтобы предсказать скорость и механизм набухания гидрогеля, которые могут различаться выше и ниже температуры стеклования полимера. Авторы полагают, что наиболее подходящие математические модели для описания кинетики набухания гидрофильных полимеров – это модели диффузии Фика и общие диффузионные модели.
Набухание геля полимера – это кинетический процесс, сопровождаемый массопереносом и механической деформацией. В работе [20] рассмотрены две теории. Обе предложенные теории – линейная и нелинейная – используются для описания кинетики набухания. Здесь мы делаем сравнение между нелинейной теорией для полимерных гелей и классической теорией линейной пороэластичности. Мы показываем, что две теории согласуются друг с другом только при условии малых отклонений от изотропного состояния геля.
Отношения между материальными свойствами линейной теории и теми же свойствами в нелинейной теории устанавливаются процедурой линеаризации.
Оба решения применяются для оценки набухания трехмерного геля и гелевой пленки на подложке. Хотя линейная теория пороэластичности является достаточно хорошей, ее можно применять при малых отношениях набухания.
Для удаления линейных ограничений предложена новая процедура, которая увязывает экспериментальные данные с результатами расчета по нелинейной теории.
В конце обсуждается indentation experiment как эффективный метод, характеризующий механические свойства и свойства переноса в полимерных гелях. Последние исследования [21] показали, что обобщенный подход Танаки сравним с линейной теорией пороэластичности Биота и Шерера [22, 18, 19].
В статье [20] показано, что в общем случае линейная теория пороэластичности не работает. Однако, для идеальных сферических систем и изотропного набухания она дает вполне надежные результаты.
В работе [23] проанализированы возможные причины экстремальной формы кинетических кривых. Было предложено рассматривать кинетику набухания как совокупность двух процессов, начинающихся одновременно, но имеющих разные скорости и заканчивающихся через разные промежутки времени. Увеличение влияния одного из процессов на степень набухания геля при завершении действия другого и приводит к изменению формы кинетической кривой. В этом случае ее невозможно описать уравнением первого порядка. В связи с этим было предложено искать зависимость изменения объема гранулы от времени как решение дифференциального уравнения второго порядка:
где: m – масса полимера, k – константа жесткости Гука и ? – параметр, характеризующий межфазное взаимодействие в геле.
Такое рассмотрение позволило получить хорошее соответствие между теоретической и экспериментальной зависимостями. В работе предложен способ нахождения коэффициентов этого уравнения.
Таким образом, исходя из выполненного обзора видно, что большинство ученых согласно, что процесс набухания гранулы полимера есть комбинация как минимум двух процессов, один из которых есть наполнение гранулы посредством раствора НМС из внешнего раствора, который протекает быстро, а насчет другого процесса (или других) авторы расходятся во мнениях.
Медленный процесс обуславливается либо трением жидкости о полимерные связи, либо упругостью полимерной сетки, либо вытеканием полимерных молекул из полимера во внешний раствор.
Видео:Химия 9 класс (Урок№33 - Полимеры.)Скачать

Кинетика набухания сшитых полимеров на основе полистирола (стр. 4 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 |
Для диффузионного механизма характеристическое время τ пропорционально квадрату исходного размера r0:
, (9)
где D — коэффициент диффузии.
Более низкая степенная зависимость отражает существование двух описанных механизмов. Таким образом, показано, что кинетика набухания полиэлектролитного геля в воде включает два различных вклада. Переход из сухого состояния в набухшее можно рассматривать, основываясь на существующих диффузионных моделях.
В работах [34, 35] отмечается, что скорость набухания гидрогеля контролируется как диффузией молекул растворителя, так и релаксацией полимерной структуры, т. е. скорость набухания пропорциональна квадрату остаточной способности набухания (SRe-SR)2:

где SR – степень набухания геля, SRe – равновесная степень набухания геля.
Проинтегрировав уравнение (10), авторы получили уравнение второго порядка – уравнение Шотта [35], в координатах которого строили кинетические кривые, выделяли на них линейные участки и определяли их наклоны:
, (11)
где k – константа скорости.
Таким образом, кинетика набухания геля в растворах солей хорошо описывается кинетическим уравнением второго порядка (11). Кроме того, наблюдали скачкообразное набухание гидрогеля при помещении его из растворов солей в воду и объясняли его создаваемым противоионами осмотическим давлением [35].
Однако известны случаи, когда при набухании полимерных гелей, вместо обычной монотонной зависимости, наблюдались колебания [36]. Кинетические аномалии такого рода получены не только на ионитах, но и на полимерах с недиссоциирующими полярными группами [37, 38]. Причина такого поведения полимеров кроется в циклическом характере проникновения воды, которая является основным веществом, влияющим на объем геля, в полимерную матрицу. Такой режим набухания может быть связан с кинетикой ионного обмена, в результате которого изменяется состав раствора и, соответственно, активность воды, с различной вязкостью внешнего раствора и раствора внутри геля, а также с другими похожими причинами. Математическое описание такого рода процессов впервые было предложено в работе [37]. Было показано, что возникновение колебаний можно объяснить теоретически, если предположить периодическое неоднородное строение поверхности полимера и учесть кинетику образования поверхностного слоя молекулярно сорбированной аминокислоты. Проведенное моделирование показало [37], что в принципе кинетические кривые сорбции могут иметь немонотонный колебательный характер. Это объясняется взаимным влиянием ионного обмена, молекулярной сорбции и встречной диффузии, создающим положительную обратную связь при колебаниях концентрации. Слабой стороной данного объяснения являются дополнительные требования к строению полимера.
В 1973 году Танака [39] предложил теорию, согласно которой набухание полимера происходит в результате одновременного протекания двух процессов – диффузии вещества внутри гранулы и релаксации полимерной сетки под воздействием трения между полимерной сеткой и гелевой жидкостью. Характерное время набухания пропорционально отношению площади к объему геля, а также коэффициенту диффузии жидкости в полимерной сетке, который определяется как отношение модуля продольного растяжения сетки к коэффициенту трения между сеткой и гелевой жидкостью. Здесь заложена существенная разница между данной теорией и теорией, существовавшей до этого, базировавшейся на предположении, что время набухания определяется коэффициентом диффузии молекул жидкости.
Эксперименты на 5% полиакриламидном геле показали хорошее совпадение с теорией, значение коэффициента диффузии, полученное из экспериментов по макроскопическому набуханию, хорошо согласуется с аналогичным коэффициентом, полученным с помощью спектроскопии рассеянного лазерного излучения.
В более поздней работе (1990 г) [40] авторы предложили механизм изменения объема полимера с учетом двух процессов, так как они считали, что изменение объема не есть чисто диффузионный процесс. Существенную роль при набухании играет модуль упругости (англ. shear modulus). Таким образом, важную роль играет геометрия геля. Исходя из аналитического решения уравнения диффузии для шарообразного зерна Ли и Танака предположили, что изменение объема геля описывается бесконечной суммой экспонент с отрицательным показателем

При этом, множители при экспонентах зависят только от качества набухающего агента (англ. swelling agent), а показатели экспонент относятся как квадраты натуральных чисел (a/1=b/4=c/9=…).
В работе формулируется теорема флуктуации-диссипации. Приводятся выражения для описания кинетических процессов на полимерах произвольной формы. В статье даются явные аналитические решения для гелей в форме бесконечного цилиндра и большого диска. Расчеты показывают, что эффективные коэффициенты диффузии для гелей в форме длинного цилиндра и для большого диска в 1.5 и в 3 раза меньше, чем для гелей сферической формы, соответственно. Если брать диаметр цилиндра, диаметр шара и толщину диска одинаковыми, то времена релаксации для гелей с малым коэффициентом упругости меньше в 2.0 и в 5.7 раза соответственно. Теория также показывает, что экспериментально измеряемые скорости протекания процесса в длинном цилиндре и в диске вдоль оси z и вдоль радиальной оси – одинаковые. Результаты хорошо согласуются с экспериментальными данными.
В статье приведены графики логарифма изменения объема гранулы от времени и показано, что они лежат на одной прямой, за исключением начального короткого (по времени) участка. По ним авторы стремились вычислять усредненные коэффициенты диффузии (пытаясь описывать протекание процесса одной экспонентой). Экспериментальные результаты показывают хорошее совпадение одной экспоненты на времени с 30 по 800 минуты. На начальном участке наблюдается отклонение от линейной зависимости. Подобные экспериментальные результаты отмечены и у других авторов. Следует отметить, что для идеальных сферических гранул модель учитывает только внутреннюю диффузию.
В работе [41] Пэппас и Браннон-Пэппас рассматривали кинетику набухания полиметакриловой кислоты и сополимера полиакриловой кислоты с полигидроксиэтилметакрилатом. Они наблюдали зависимость кинетики набухания от рН раствора и от ионной силы в этих гелях. Авторами была разработана модель для описания кинетики набухания ионных форм гидрогелей в ответ на изменения ионной силы раствора.
Когда гель набухает при изменении рН, существует соответствующее изменение объема или длины полимерной цепи. Основываясь на набухании, деформация в геле, ε, может быть вычислена в любой момент времени набухания как:

где l — длина в любое время и l0 — начальная длина.
По принципу суперпозиции Больцмана и деформация в зависимости от изменения pH или ионной силы раствора может быть вычислена как:

где 

Предполагая, что набухание в геле изотропно, соотношение объёмов при набухании геля может быть записано в виде:

где Vs(t) – объём набухшего геля в любой момент времени, а Vd – начальный объём сухого полимера. Комбинируя 15 и 16, набухание геля в зависимости от изменения pH или ионной силы раствора может быть описано как:

Авторы данной работы показали, что можно предсказать набухание как нейтральных, так и ионных форм гелей при различных условиях.
В работе [42] исследована кинетика набухания и сжатия дисков поливинилацетата, набухающих в изопропиловом спирте при различных температурах. При этом определялся общий коэффициент диффузии и отношение модуля упругости к продольному осмотическому давлению на базе теории Ли и Танаки. Авторы наблюдали хорошее соответствие между теоретическими и экспериментальными результатами макроскопического изменения объема.
В 1997 г. исследователи из северного Техаса предложили свой механизм релаксации объема полимерной гранулы к ее равновесному значению. В статье [43] с помощью математического моделирования анализируется кинетика набухания геля с учетом движения как раствора НМС, так и полимерной сетки. Эта модель не использует подход двух процессов от Ли и Танака, в котором движение раствора учитывается неявно. Аналитическое решение для описания движения раствора и сетки находится из системы уравнений общей диффузии для объектов – бесконечный цилиндр и большой плоский диск. Для цилиндрического объекта скорость движения раствора пропорциональна радиусу в радиальном направлении и координате z вдоль оси симметрии цилиндра. Авторы установили, что процесс набухания в цилиндре и на диске идет медленнее, чем ожидается, основываясь на теории чисто внутренней диффузии. В этой статье авторы модифицировали и расширили подход Ли и Танаки, путем добавления учета движения как раствора, так и полимерной сетки.
В 2000 г. финские химики изучали процессы набухания полиуретанов (ПУ) различных типов [44]. Они показали, что только малая часть таких реакций может быть описана с помощью кинетических уравнений первого порядка. Кроме того, ими отмечено, что параметры процесса существенно зависят от температуры. В соответствии с анализом кинетики сшитых полимеров, некоторые из ПУ описываются кинетическим уравнением первого порядка, а другие – кинетическим уравнением второго порядка. Поведение набухания алифатических ПУ описывалось посредством нахождения доли геля и степени сшивки после обработки образца. Предложены уравнения типа:
Видео:ПолимерыСкачать

Набухание сетчатых полимеров
Цель работы. Определение плотности энергии когезии (ПЭК) неполярного и полярного каучуков по данным набухания. Установление влияния степени полярности каучука на величину энергии когезии.
Макромолекулы полимера представляют собой длинные цепочки из повторяющихся по химической природе звеньев. Звено макромолекулы содержит определенное число атомов разной химической природы, объединенные в некоторую химическую и пространственную структуру с помощью ковалентных (ионных, водородных) связей. Каждый атом звена имеет положительно заряженное ядро и отрицательно заряженную многоуровневую электронную оболочку. Движение электронов по орбиталям вокруг ядра приводит к возникновению диполей с очень коротким временем «жизни».
Взаимодействие этих диполей определяет появление так называемых дисперсионных связей внутри — и/или межмолекулярного характера. Каждый атом, входящий в состав звена макромолекулы имеет свою электронную плотность в соответствии со своей химической природой и природой звена в целом. По этой причине звено макромолекулы имеет постоянный электрический диполь, величина которого зависит от его химической природы и пространственного расположения атомов. Постоянные диполи «своих» и «чужих» звеньев макромолекул взаимодействуют между собой, образуя ориентационные связи.
Еще один тип физических ван-дер-ваальсовых связей возникает, когда «сильный» постоянный диполь одного звена макромолекулы наводит за счет поляризации диполь в другом звене.
Такой тип связи называется индукционным. Наиболее большой по энергии взаимодействия среди физических связей является водородная связь, которая образуется между сильно электроотрицательными атомами (F ,O, N, S, Cl ) и атомами водорода.
Для оценки величины суммарного межмолекулярного взаимодействия полимерных молекул пользуются величиной плотности энергии когезии. Применительно к низкомолекулярным жидкостям ПЭК определяется как молярная энергия испарения, деленная на молярный объем. Для каждой низкомолекулярной жидкости известен или может быть рассчитан параметр растворимости s , который равен квадратному корню из плотности энергии когезии:
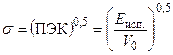
Для полимеров параметр растворимости определяют обычно из данных по равновесному набуханию. Параметры растворимости полимера и растворителя равны, если для данного растворителя наблюдается максимально возможная степень набухания полимера. Поэтому, определив степень набухания полимера в ряду растворителей с известными значениями sр , строят зависимость величины степени набухания полимера от параметра растворимости растворителя. При этом получают кривую, напоминающую по виду гауссову, центрированную относительно некоторого значения параметра растворимости s, при котором набухание максимально. Лучшим считается тот растворитель, в котором степень набухания максимальна при условии отсутствия теплового эффекта смешения или изменения объема системы. Суммарная энергия межмолекулярного взаимодействия складывается из энергий ориентационного, индукционного, дисперсионного и водородного взаимодействий. Вклад каждого вида взаимодействий может быть различным и зависит от природы полимера. В системе слабополярных макромолекул основными являются силы дисперсионного взаимодействия, но с увеличением полярности молекул все большее значение приобретают силы ориентационного взаимодействия.
Значение ПЭК зависит от химической структуры полимера. Полимеры, имеющие более сложную структуру звена, как правило, обладают большим значением ПЭК, и наоборот.
Интенсивность межмолекулярного взаимодействия является решающим фактором, лежащим в основе разделения полимеров на эластомеры, пластомеры и волокна. ВМС с наиболее интенсивными межмолекулярными взаимодействиями, склонные к образованию упорядоченных областей, являются типичными волокнообразующими материалами. Для них ПЭК может достигать весьма высоких значений. Влияние регулярности структуры и энтропийного фактора служит причиной возможного исключения из этих закономерностей.
Из значения плотности энергии когезии каучука можно найти параметр его растворимости σк:

Для определения численного значения ПЭК каучука по данным равновесного набухания строится графическая зависимость в координатах: степень набухания полимера Qр – параметр растворимости растворителя σр .
Построенная кривая имеет максимум, соответствующий по оси абсцисс параметру растворимости полимера σк:
|
|
Рис. 17. Типичный график зависимости количества поглощенного
растворителя от параметра растворимости растворителя
Посуда, реквизиты и образцы: аналитичекие весы, бюксы, эфир, толуол, гептан, гексан, дихлорэтан, изопропиловый спирт, ацетон, тетрахлорметан, другие растворители, вулканизаты каучуков СКИ-3 и СКН-40, секундомер, пинцет, фильтровальная бумага.
В эксперименте используются слабо структурированные ненаполненные вулканизаты, которые способны хорошо набухать в ряде растворителей, но не растворяться в них из-за наличия поперечных связей. Для определения ПЭК берут вулканизаты двух каучуков и растворители согласно рекомендациям таблицы 4. Образцы вулканизатов каучуков вырезают в виде квадратиков размером 3´3 мм.
Для каждого изучаемого вулканизата вырезаются 5 одинаковых образцов. Каждый образец взвешивают на аналитических весах и помещают в бюкс, куда вносится по 8 мл одного из растворителей, рекомендованных в таблице. Каждый из бюксов номеруется. В рабочей тетради, согласно номеру бюкса, фиксируется тип полимера и растворителя, а так же вес исходного вулканизата – m0.
Бюксы, с содержащимся в них полимером и растворителями, оставляют до следующего занятия, но не менее чем на две недели. Бюксы желательно убрать в шкаф, поставив их на бумагу с надписью, указывающей фамилии и № группы студентов, дату выполнения работы.
Через две недели каждый из образцов поочередно вынимают пинцетом из бюксов, обмакивают в эфир, промокают фильтровальной бумагой, замечают по секундомеру время, и по истечении 30 секунд образец взвешивают на весах, определяя массу набухшего образца mн.
Объемную степень набухания в условиях равновесия (Qp) рассчитывают по формуле:

значения rк и rр находим из таблицы 5.
По результатам эксперимента заполняется таблица 3.
Таблица 3
Зависимость объемной степени набухания каучука от растворителя
| Растворитель | rр , г/см 3 | sр , (МДж/м 3 ) 1/2 | m0 , г | mн , г | Qр |
Для нахождения параметра растворимости полимера строят графическую зависимость (Qр ; sр), и точка максимума на кривой соответствует параметру растворимости полимера sк, следовательно, согласно уравнению (14),

Таблица 4
Рекомендуемые типы растворителей для определения плотности энергии когезии разных каучуков
| Каучук | Раствори- тели | s (МДж/м 3 ) 0,5 | Каучук | Растворители | s (МДж/м 3 ) 0,5 |
| Натуральный | Пентан | 14,19 | Бутадиен–нитрильный СКН–40 | Бензол | 18,86 |
| Октан | 15,546 | Хлорбензол | 19,43 | ||
| Циклогексан | 16,875 | Этилацетат | 18,61 | ||
| Толуол | 18,35 | Ацетон | 19,92 | ||
| Бензол | 18,86 | Этиловый спирт | 26,33 | ||
| C CL4 | 17,65 | 1,2–дихлорэтан | 20,37 | ||
| Бутилкаучук | Пентан | 14,2 | Полисульфидный | Толуол | 18,35 |
| Гептан | 15,3 | Бензол | 18,86 | ||
| Октан | 15,55 | Хлорбензол | 19,43 | ||
| Циклогексан | 16,88 | Бутиловый спирт | 22,03 | ||
| П.–ксилол | 18, 47 | ||||
| Хлоропреновый | Циклогексан | 16,875 | Силоксановый | Пентан | 14,2 |
| П.–ксилол | 18,47 | Гексан | 14,99 | ||
| О.–ксилол | 18,47 | Гептан | 15,3 | ||
| Бензол | 18,86 | Октан | 15,55 | ||
| 1,2–дихлорэтан | 20,37 |
Таблица 5 Плотности растворителей и каучуков
| Растворитель | rр , г/см 3 | Растворитель | rр , г/см 3 |
| Ацетон | 0,79 | Толуол | 0,88 |
| Бензол | 0,88 | Трихлорметан | 1,50 |
| Бутиловый спирт | 0,81 | Тетрахлорметан | 1,60 |
| Гексан | 0,66 | Эфир диэтиловый | 0,79 |
| Гептан | 0,68 | Этиловый спирт | 0,79 |
| Дихлорэтан | 1,25 | Этилацетат | 0,90 |
| Ксилол (о.-, п.-) | 0,88 | Циклогексан | 0,78 |
| Каучук | rк , г/см 3 | Каучук | rк , г/см 3 |
| СКИ-3 | 0,92 | СКН–40 | 0,97 |
Обсуждение полученных результатов
Вначале данного раздела студенту следует дать краткое определение понятию плотности энергии когезии. Затем, по построенному графику зависимости Qp = f(σp) найти значение параметра растворимости каучуков σк, при котором объемная степень набухания максимальна. На занятии выдаются вулканизаты на основе малополярного каучука СКИ-3 и сильно полярного СКН-40.
Анализируя полученные данные, нужно сравнить значения ПЭК резин на основе каучуков СКИ-3 и СКН-40. Ключевым моментом данной работы является выведение качественной зависимости ПЭК от химической структуры полимера. Под химической структурой полимера подразумевается рассмотрение, главным образом, наличия в макромолекулах полярных атомов или групп, а также влияние степени разветвленности и длины макроцепи. На силу межмолекулярных взаимодействий также влияют типы связей, которые образует полимер с растворителем.
Поскольку энергия связи возрастает с повышением поляризуемости и дипольного момента, требуется привести значения показателей, характеризующих силу притяжения между группами в полимере. Одним из таких показателей является константа
притяжения Gi. Существенное влияние на данный показатель оказывают наличие двойных связей и степень разветвленности макроцепи. Необходимо выявить зависимость между показателем Gi и параметром растворимости полимера.
Пример. СКИ-3- каучук, дипольный момент которого близок к нулю. Объемная степень набухания Qp в полярном растворителе имеет практически минимальное значение.
Значение константы притяжения групп заместителей в полимере составляет Gi = (-CН3 -) =438 (мк ∙ Дж ∙ м 3 ) 0,5 , а Gi = (-CN-) =838 (мк ∙ Дж ∙ м 3 ) 0,5 , что обусловлено присутствием –СN- группы в бутадиен-нитрильном каучуке. Таким образом, для удаления взаимодействующих молекул на расстояние, при котором будет отсутствовать межмолекулярное взаимодействие необходимо меньшее количество работы в случае использования СКИ-3 по сравнению с СКН-40, соответственно значение ПЭК изопренового каучука будет меньшим.
Кратко и лаконично перечисляются основные итоги раздела «Обсуждение результатов». По экспериментальным данным определяется значения ПЭК для каучуков СКИ-3 и СКН-40. Вывод должен касаться зависимости величины ПЭК от химической структуры полимера.
1. Кирпичников, П.А. Химия и технология синтетического каучука /П.А. Кирпичников, Л.А. Аверко-Антонович, Ю.О. Аверко-Антонович. – Л.: Химия, 1970. – 528с.
2. Догадкин, Б. А. Химия эластомеров / Б.А.Догадкин, А.А. Донцов, В.А.Шершнев. – М.: Химия, 1981. – 376 с.
3. Практикум по высокомолекулярным соединениям. – М.: Химия, 1985. – 224 с.
Лабораторная работа № 5
ВЛИЯНИЕ ПРИРОДЫ РАСТВОРИТЕЛЯ
НА СКОРОСТЬ НАБУХАНИЯ СЕТЧАТОГО ПОЛИМЕРА
Цель работы.Измерение скорости и определение постоянной набухания сетчатого эластомера в различных растворителях.
Установление влияния природы растворителя на величину и скорость набухания сетчатого эластомера.
Установление склонности к набуханию имеет большое значение для оценки качества некоторых видов каучуков, применяемых для изготовления резиновых изделий, работающих в среде растворителей.
Первой стадией растворения любого полимера является его
Различают ограниченное и неограниченное набухание.
Полимеры пространственно-сетчатого строения не могут полностью растворяться из-за наличия поперечных химических связей. Они способны лишь ограниченно набухать, образуя гели. Увеличение количества поперечных связей приводит к уменьшению способности полимера поглощать низкомолекулярную жидкость; при наличии густой пространственной сетки полимер полностью теряет способность набухать. Это можно проиллюстрировать рядом примеров. Так, при увеличении содержания серы в полимере способность вулканизатов к набуханию непрерывно уменьшается. Эбонит (вулканизат, содержащий около 32 % серы) совершенно не набухает. В данной работе, как впрочем, и в большинстве работ этого пособия, студентам выдаются образцы резин на основе различных по химическому строению каучуков.
Ограниченным набуханием называется процесс взаимодействия полимеров с низкомолекулярными жидкостями, ограниченный только стадией их поглощения полимером; самопроизвольного растворения полимера не происходит. При этом образуются две сосуществующие фазы. Одна фаза представляет собой раствор низкомолекулярной жидкости в полимере, другая является чистой низкомолекулярной жидкостью (если полимер совсем не растворяется) или разбавленным раствором полимера в низкомолекулярной жидкости. Эти фазы разделены ясно видимой поверхностью раздела и находятся в равновесии.
Для линейных полимеров этот процесс аналогичен ограниченному смешению жидкостей: при определенных условиях (температуре, концентрации компонентов) набухание ограниченно, но при соответствующем изменении условий оно может перейти в неограниченное растворение. Одним из таких условий является повышение температуры, способствующее разрушению физических связей между звеньями цепей.
Главным условием образования гомогенной, термодинамически устойчивой системы является степень сродства между полимером и растворителем. А она, в свою очередь, зависит от природы, как самого полимера, так и растворителя.
Если звенья цепей и молекулы растворителя близки по полярности, то энергия взаимодействия между однородными и разнородными молекулами примерно одинакова – происходит набухание (неограниченное или ограниченное). Если звенья цепи полимера и молекулы растворителя сильно различаются по полярности, то набухание происходит небольшое и растворения не наблюдается.
Неполярные полимеры (полиизопрен, полибутадиен) неограниченно смешиваются с предельными углеводородами (гексан) и не взаимодействуют с сильнополярными жидкостями (водой, спиртом). Полярные полимеры (целлюлоза, поливиниловый спирт) совершенно не взаимодействуют с углеводородами и хорошо набухают в полярных жидкостях.
Склонность полимера к растворению увеличивается с ростом гибкости его цепи. Увеличение температуры способствует увеличению гибкости цепей, что в свою очередь, облегчает отделение макромолекул друг от друга и ускоряет скорость их диффузии в растворитель. Поэтому полимеры с гибкими цепями, как правило, неограниченно набухают, т.е. растворяются. Большой гибкостью обладают полимеры с низким значением потенциальногобарьера вращения, не имеющие громоздких боковых разветвлений, полярных заместителей.Все эти факторы ведут, в конечном итоге, к уменьшению сил внутри- и межмолекулярного взаимодействия и повышению скорости набухания. С увеличением молекулярной массы полимера возрастает энергия взаимодействия между цепями в полимергомологическом ряду, следовательно, способность к растворению в одном и том же растворителе будет понижаться.
При рассмотрении влияния исходного фазового состояния полимера необходимо отметить, чтокристаллические полимеры растворяются значительно хуже, чем аморфные. Это объясняется наличием большого межмолекулярного взаимодействия из-за дальнего порядка расположения молекул. В этом случае для отрыва цепей друг от друга необходимо одновременно нарушить большое число физических связей, что требует значительной затраты энергии. Поэтому при комнатных температурах кристаллические полимеры, как правило, не растворяются даже в жидкостях, сходных по полярности.
Процесс растворения полимера в растворителе состоит из ряда последовательных стадий. На первой, молекулы растворителя, из-за значительно меньших размеров по сравнению с макромолекулами, проникают вглубь образца полимера в первую очередь в наименее плотно упакованные области поверхностных слоев. При этом молекулы растворителя вступают в физическое взаимодействие со звеньями макромолекул (идет сольватация). Визуально это проявляется в виде набухания полимера, так как образование сольватной «шубы» на макромолекулах из молекул растворителя раздвигает их и увеличивает объем. Увеличение расстояния между звеньями макромолекул приводит в конечном итоге к полному разрушению межмолекулярных физических связей. По этой причине макромолекулы полимера, не связанные с другими макромолекулами физическими связями, получают возможность диффундировать вглубь объема растворителя. Когда число таких макромолекул становится большим, это проявляется в виде уменьшения ранее достигнутой максимальной степени набухания. С этого момента можно уже с уверенностью заявлять, что стадия набухания завершилась и началась стадия растворения. Понятно, что полимеры сетчатого строения могут только ограниченно набухать в растворителях.
С практической точки зрения очень важно знать способность сшитых полимеров к набуханию в различных жидких и парообразных средах. Эта способность оценивается по степени набухания, которая выражается количеством поглощенной полимером жидкости (или ее пара), отнесенным к единице массы или объема полимера.
Состояние набухания характеризуют степенью набухания, которую определяют как количество поглощенной полимером жидкости, отнесенной к единице массы или объема полимера:

где m0, V0 – масса и объем исходного полимера;
m1, V1 – масса и объем набухшего полимера.
На рис. 18 приведена типичная зависимость степени ограниченного набухания полимера от времени.
Рис. 18. Типичная зависимость степени набухания от времени
Максимальная или равновесная степень набухания (qmax)
определяется природой полимера и растворителя (сродством между ними), и густотой пространственной сетки полимера (при ее наличии).
Скорость набухания полимера лимитируется скоростью взаимной диффузии компонентов системы и для полимеров, находящихся в исходном высокоэластическом состоянии, обычно удовлетворительно описывается кинетическим уравнением первого порядка:

где k – постоянная набухания;
q¥ – максимальная (равновесная) степень набухания;
q – степень набухания в наблюдаемый момент времени.
После интегрирования уравнения (16) получим:

По тангенсу угла наклона прямолинейной зависимости 
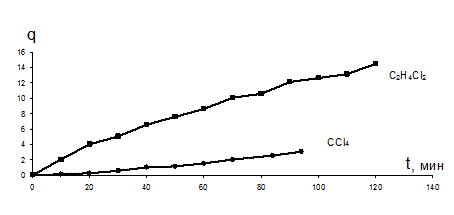
Реактивы, приборы и образцы: серный вулканизат каучука СКН–40, CCl4, C2H4Cl2, дилатометры, секундомер.
Скорость набухания определяют объемным методом, используя дилатометры.
Две небольшие пластинки резины (по 0,1–0,2 г) взвешивают на аналитических весах и помещают в дилатометры, один из которых заполняют CCl4, а другой – C2H4Cl2.
Набухание резины измеряют параллельно в двух растворителях, проводя замеры объема поглощенной низкомолекулярной жидкости через каждые 10 минут в течение 2 часов. Результаты эксперимента заносятся в таблицу 6.
Таблица 6
Экспериментально-расчетные данные процесса набухания
| t, с | DV |  | 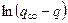 |
Строят графики зависимостей степени набухания (рис.19) и величины 
Обсуждение полученных результатов
В результате проведения эксперимента и расчетов студент получает численные значения qmax, k для серного вулканизата СКН-40, набухшего в CCl4 и C2H4Cl2. В данном разделе он должен объяснить различия в полученных значениях, рассматривая, в первую очередь, такое важное понятие как степень термодинамического сродства между полимером и растворителем.
С этой целью требуется вначале сделать качественный вывод о полярности каучука СКН-40 и растворителей. Для этого необходимо начертить структурную формулу звена СКН-40 и структурные формулы CCl4 и C2H4Cl2. Затем можно подтвердить сделанные качественные заключения о степени сродства каучука с растворителями сравнением их параметров растворимости s. Данные по величинам s растворителей можно взять в таблице 4 работы 4.
Рис.19. Зависимость степени набухания q от времени t
Следует учесть, что кинетика набухания определяется не только структурой исследуемого полимера и типом растворителя, но и геометрической формой образца. По этой причине для сравнения степени набухания различных полимеров необходимо использовать образцы одинаковые по размерам и форме. Желательно объяснить данный факт. Не следует забывать и о влиянии физического и фазового состояний полимера на склонность к набуханию.


В данной работе необходимо сделать вывод о влиянии термодинамического сродства полимера и растворителя на скорость и максимальную степень набухания.
1.Кирпичников, П.А. Химия и технология синтетического каучука / П.А. Кирпичников, Л.А. Аверко-Антонович, Ю.О. Аверко-Антонович. – Л.: Химия, 1970. – 528с.
2. Практикум по высокомолекулярным соединениям. – М.: Химия, 1985. – 224 с.
Лабораторная работа № 6
Оценка параметров пространственной сетки сшитого полимера по степени
равновесного набухания
Цель работы.Исследование структуры и степени сшивания вулканизатов на основе различных по химической природе каучуков.
При наличии в полимере межмолекулярных химических связей набухание не может быть неограниченным. При контакте с низкомолекулярным растворителем сетчатый полимер ограниченно набухает, и равновесная степень набухания определяется плотностью поперечных связей и качеством растворителя.
Флори и Ренер провели теоретическое рассмотрение процесса набухания полимера сетчатого строения. Оказалось, что набухание такого полимера происходит до тех пор, пока осмотическая сила растворителя, проникающего в фазу полимера, не уравновесится упругой силой полимерной сетки.
Условию равновесия (моменту равновесного набухания) соответствует состояние трехмерной сетки, описываемое уравнением Флори–Ренера:

где Vk – объемная доля полимера в набухшем образце;
V1 – мольный объем растворителя;
fy – функциональность узла сшивания; для тетрагональной сетки равна 4.
m – параметр взаимодействия каучука с растворителем.
Мc – молекулярная масса отрезка цепи между узлами сетки;
ρ – плотность эластомера.
Из уравнения (18) следует:

Пробы и реактивы:исследуют 2–3 вулканизата каучука, завулканизованных с применением различного количества серы и различных типов вулканизующих систем. Набухание образцов изучают в подходящем растворителе, для которого параметр взаимодействия m растворитель–полимер близок к 0,5 (см. табл. 8).
Для каждого типа вулканизата подготавливают по два образца, желательно, чтобы один образец имел форму квадрата с размером стороны 3 мм, а другой – прямоугольника размером 2´3 мм. Образцы взвешивают на торсионных весах, вес образца m0 определяют по разности весов чашки с образцом и пустой чашки.
Взвешенные образцы помещают в бюксы (по 2 параллельных образца в один бюкс), предварительно пронумеровав их. В каждый из бюксов добавляют по 8 мл растворителя. Бюксы закрывают крышками и вместе с образцами оставляют до следующего занятия.
Все бюксы устанавливают в шкафу на бумагу, где указаны фамилии студентов, № группы, дата проведения работы и тип растворителя. Шифр бюкса и вес образцов заносится в рабочую тетрадь. Через неделю, каждый из образцов поочередно, пинцетом вынимают из бюкса, обмакивают в эфир, промокают фильтровальной бумагой, замечают по секундомеру 30 секунд. По истечении этого времени образец взвешивают на торсионных весах и определяют вес набухшего образца mH.
Для расчета параметра MC пространственной сетки полимера по формуле (19) используют значение равновесного набухания.
Объемную долюисходного полимера в набухшем геле рассчитывают по формуле:

Значения rК и rР определяют из таблицы 9. Зная МС, рассчитывают степень сшивания j резин, то есть среднее число отрезков между узлами пространственной сетки, приходящейся на 1 макромолекулу эластомера:

где М0 – молекулярная масса эластомера до сшивания.
При этом предполагается, что вулканизация протекала без деструкции исходного полимера.
Полученные данные и результаты вычислений заносят в таблицу 7.
Таблица 7
Экспериментальные данные степени сшивания
| m0 | mH | 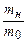 |  |  |  |  | 1–VK | ln(1–VК) | MС | j |
Сравнивая полученные значения MС и j, сделать выводы о степени структурирования изучаемых вулканизатов каучука.
Обсуждение результатов экспериментов
Данная работа проводится с образцами резин на основе полярного (СКН-40) и малополярного (СКИ-3) каучуков, подвергнутых равновесному набуханию каждый в двух растворителях, которые различаются по степени термодинамического сродства к набухаемому образцу.
Основная цель работы заключается в выяснении соотношения плотностей химической и физической сетки в резинах на основе полярного и неполярного каучуков.
Как правило, Vk равна 0,25 или немного меньше в случае равновесного набухания среднесшитого сетчатого полимера в растворителе с близким значением параметра растворимости.
В этом случае, рассчитанная по формуле (19) величина МС будет отражать плотность химической сетки. В другом растворителе, с более далеким значением параметра растворителя по сравнению с параметром растворимости каучука, Vк будет больше 0,25 и найденное значение МС будет отражать плотность сетки за счет химического сшивания и физического межмолекулярного взаимодействия. Рассчитав значения j по уравнению (21) для обоих случаев, можно в итоге определить доли химической и физической сетки в каждом из сетчатых эластомеров. Обсуждение результатов после получения этих данных должно касаться вопроса влияния химической природы каучука на уровень межмолекулярного физического взаимодействия в нем. Кроме того, нужно обратить внимание на наличие или отсутствие в испытываемом сетчатом эластомере активного наполнителя (технического углерода), способного образовывать с макромолекулами эластомера физические связи. При этом может образоваться такой вид НДС, как сажекаучуковая структура.
При обсуждении полученных результатов студент также должен обратить свое внимание на возможность сохранения в набухшем сетчатом эластомере кристаллических структур, если исходный эластомер способен кристаллизоваться.
Поскольку студентам при выполнении лабораторной работы выдаются сетчатые эластомеры разной степени сшивания, за счет неодинаковой дозировки сшивающего агента, то обязательно следует проанализировать влияние густоты химической сетки на уровень межмолекулярного физического взаимодействия.
Пример. В работе выдаются образцы на основе каучуков СКН-40 с 1 и 0,5 масс.ч и СКИ-3 с 1 и 0,5 масс.ч серы на 100 масс.ч каучука. Образцы вулканизатов СКИ-3 и СКН-40 подвергаются в течении не менее двух недель равновесному набуханию в растворителях, подобранных согласно значению m. После расчета Мс и φ по данным равновесного набухания необходимо рассчитать доли химических и физических сшивок в вулканизатах СКН-40 и СКИ-3 и сделать соответствующие выводы.
Кратко и лаконично перечисляются основные итоги раздела «Обсуждение результатов». По найденным значениям Мс и φ и степени набухания в вулканизатах на основе каучуков СКИ-3 и СКН-40 делаются выводы о влиянии полярности каучуков на значения этих показателей.
Вопросы для самоподготовки и самоконтроля
1. Перечислите признаки истинных растворов полимеров.
2. Каковы особенности термодинамики растворения полимеров?
3. Дайте определение ограниченному и неограниченному набуханию полимеров.
4. Охарактеризуйте основные особенности процесса набухания полимеров.
5. Каково практическое значение растворов полимеров, какую роль они играют в технологических процессах синтеза и переработки полимеров?
1.Кирпичников, П.А. Химия и технология синтетического каучука / П.А. Кирпичников, Л.А. Аверко-Антонович, Ю.О. Аверко-Антонович. – Л.: Химия, 1970. – 528с.
2. Практикум по высокомолекулярным соединениям. – М.: Химия, 1985. – 224 с.
Таблица 8
Значения параметров взаимодействия полимер-растворитель при комнатной температуре
| Тип каучука | Растворитель | m | Плотность вулканизата (rк), г/см 3 | |
| Натуральный Изопреновый СКИ-3 | Бензол | 0,421 | 0,91 0,92 | |
| Гексан | 0,480 | |||
| 1,1–дихлорэтан | 0,482 | |||
| Дихлорэтан | 0,494 | |||
| Гептан | 0,436 | |||
| CCl4 | 0,450 | |||
| Бутилкаучук | Циклогексан | 0,433 | 0,92 | |
| Гептан | 0,468 | |||
| Бензол | 0,50 | |||
| Декан | 0,519 | |||
| Этиленпропиленовый | Пентан | 0,440 | 0,86-0,87 | |
| Толуол | 0,490 | |||
| Этилбензол | 0,490 | |||
| Бензол | 0,580 | |||
| Силоксановый (диметилсилоксановый) | Пентан | 0,430 | 2,13 | |
| Толуол | 0,465 | |||
| Трихлорметан | 0,470 | |||
| Бензол | 0,520 | |||
| Бутадиен–нитрильный | СКН–18 | Этилбромид | 0,416 | 0,943 |
| Диоксан | 0,454 | |||
| Тетрахлорметан | 0,478 | |||
| СКН–26 | Этилбромид | 0,426 | 0,962 | |
| Диоксан | 0,455 | |||
| Тетрахлорметан | 0,686 | |||
| СКН–40 | Этилбромид | 0,489 | 0,986 | |
| Диоксан | 0,498 | |||
| Бутадиен-стирольный | СКС–30 | Дихлорметан | 0,474 | 0,944 |
| Циклогексан | 0,482 | |||
| Дибромметан | 0,497 | |||
| Диоксан | 0,538 | |||
| Хлоропреновый | Дихлорэтан | 0,533 | 1,21-1,25 |
Таблица 9
Параметр растворимости и плотность различных растворителей при комнатной температуре
1 (Дж/моль) – 0,2390 кал/моль
| Растворитель | Параметр растворимости sр | |
| (кал/см 3 ) 0,5 | (Дж/см 3 ) 0,5 | |
| Ацетон | 9,74 | 40,75 |
| Бензол | 9,22 | 38,58 |
| Бутанол | 10,77 | 45,06 |
| Гексан | 7,33 | 30,67 |
| Гептан | 7,48 | 31,34 |
| 1,2–дихлорэтан | 9,96 | 41,73 |
| Диэтиловый эфир | 7,74 | 32,43 |
| Октан | 7,60 | 31,84 |
| о.–ксилол | 9,03 | 37,84 |
| п.–ксилол | 9,03 | 37,84 |
| Пентан | 6,94 | 29,03 |
| Тетрахлорметан | 8,63 | 36,1 |
 Толуол Толуол | 8,97 | 37,53 |
| Этанол | 12,87 | 53,84 |
| Этилацетат | 9,10 | 38,07 |
| Циклогексан | 8,25 | 34,52 |
Лабораторная работа № 7
ОПРЕДЕЛЕНИЕ МОЛЕКУЛЯРНОЙ МАССЫ
КАУЧУКА
Цель работы. Определение молекулярной массы полиизопрена вискозиметрическим методом на вискозиметре Убеллоде.
Молекулярная масса – это одна из важнейших характеристик, определяющая физические, физико-химические и физико-механические свойства полимера, такие как прочность, твердость, температуростойкость. Существуют несколько методов определения молекулярной массы каучука, но наиболее оптимальным в лабораторных условиях является вискозиметрический метод.
🔥 Видео
#4 Кодирующие и некодирующие области | Новый тип задач | Задачи 27 на синтез белка | ЕГЭ БиологияСкачать

Аржаков М. С. - Высокомолекулярные соединения - Синтез полимеровСкачать

5.1. Адсорбция. Классификация адсорбцииСкачать

Аржаков М. С. - Высокомолекулярные соединения - Синтез полимеровСкачать

Лекция 3-1. Растворы полимеров.Скачать

Аржаков М. С. - Высокомолекулярные соединения - Химия растворов полимеровСкачать

Полимеры. Ч.2-5. Номенклатура полимеров.Скачать

Аржаков М. С. - Высокомолекулярные соединения - Конформация макромолекулярной цепиСкачать

Черникова Е.В. "От синтеза макромолекул к получению полимерных материалов"Скачать

Полимеры 15.03Скачать

Матвеенко В. Н. - Коллоидная химия - РеологияСкачать

Полимеры. Ч.3-1. Реакции полимеризации и поликонденсации (классификация).Скачать

Лекция С.Д. Зайцева: «Новые методы получения полимеров»Скачать

Аржаков М. С. - Высокомолекулярные соединения - Механика полимеровСкачать

Лекция 4 Чалых А Е Физическая химия полимеровСкачать

Полимеризация и поликонденсация | Химия ЕГЭ с Юлией ВишневскойСкачать

Реология материалов. ВведениеСкачать