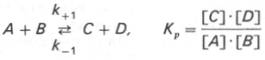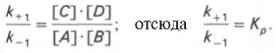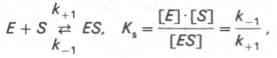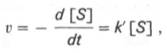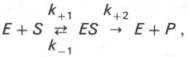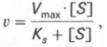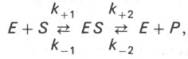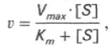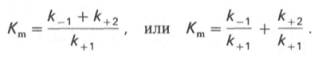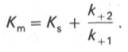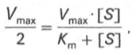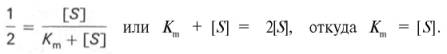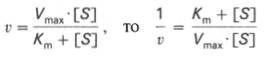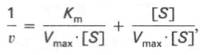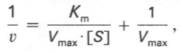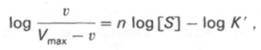Кинетика ферментативных реакций биохимия уравнение (6 видео)

Зависимость фермента от количества субстрата описывает ферментативная кинетика

Содержание

Уравнения Михаэлиса-Ментен и Лайнуивера-Берка
БИОХИМИЯ УЧЕБНИК ДЛЯ ВУЗОВ — Е. С. Северина — 2004
РАЗДЕЛ 2. ЭНЗИМОЛОГИЯ
V. Основы кинетики ферментативных реакций
Кинетика ферментативных реакций
💥 Видео

Уравнения Михаэлиса-Ментен и Лайнуивера-Берка

Общую теорию ферментативной кинетики и зависимость активности фермента от субстрата.описали Л.Михаэлис и М.Л.Ментен, выразив его в своем уравнении. Бриггс и Холдейн усовершенствовали их уравнение, введя введя в него константу Михаэлиса (Km), определяемую экспериментально.

Уравнение Михаэлиса-Ментен показывает взаимосвязь максимально возможной скорости, реальной скорости реакции, константы Михаэлиса и концентрации субстрата. Так как пользоваться графиком, построенным в прямых координатах V и [S] для точных расчетов неудобно, то Г.Лайнуивер и Д.Бэрк преобразовали уравнение Бриггса–Холдейна в обратные координаты.

Уравнение Михаэлиса-Ментен

Уравнение Лайнуивера-Бэрка

На самом деле уравнение Михаэлиса-Ментен в данном виде предложили Бриггс и Холдейн, но в честь основоположников оно носит название Михаэлиса-Ментен.

Выделяют три основных решения уравнения Михаэлиса-Ментен:

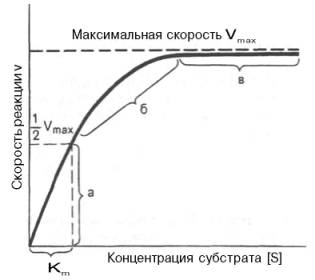
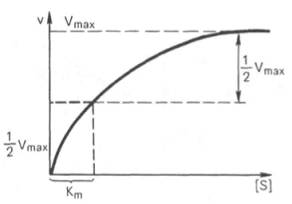
1. Концентрация субстрата равна величине константы Михаэлиса ([S] = Km).
В этом случае, решая уравнение Михаэлиса-Ментен, получаем, что скорость реакции V будет равна половине максимальной Vmax.(V = ½ Vmax).

В математическом смысле Km соответствует концентрации субстрата при которой скорость реакции равна половине максимальной. Ее биологический смысл заключается в характеристике сродства фермента к субстрату, а именно: увеличение величины Кm означает снижение сродства фермента к субстрату.

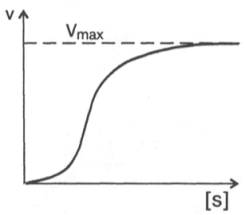
2. Концентрация субстрата значительно больше Km ([S] >> Km). В этом случае величиной Km можно пренебречь, при решении получим, что скорость реакции максимальна (плато на графике).

3. Концентрация субстрата значительно меньше Km ([S]

Видео:USMLE Step 1 - Фармакология: кинетика ферментов | уравнение Михаелиса - Ментена и не толькоСкачать

БИОХИМИЯ УЧЕБНИК ДЛЯ ВУЗОВ — Е. С. Северина — 2004

Видео:Биохимия | Кинетика ферментативных реакций: константа Михаэлиса и график Лайнуивера-БеркаСкачать

РАЗДЕЛ 2. ЭНЗИМОЛОГИЯ

V. Основы кинетики ферментативных реакций

Кинетика ферментативных реакций — раздел энзимологии, изучающий зависимость скорости химических реакций, катализируемых ферментами, от химической природы реагирующих веществ, а также от факторов окружающей среды.

Для измерения каталитической активности ферментов используют такие показатели, как скорость реакции или активность фермента. Скорость ферментативной реакции определяется изменением количества молекул субстрата или продукта за единицу времени. Скорость ферментативной реакции — мера каталитической активности фермента, её обозначают как активность фермента.

Математически скорость ферментативной реакции выражается в изменении концентрации субстрата (уменьшение) или продукта (увеличение) за единицу времени:

На начальном этапе [0 — t₀] скорость реакции прямо пропорциональна времени и имеет линейную зависимость. Графически изменение скорости ферментативной реакции определяется тангенсом угла наклона касательной к кривой профиля реакции. Чем больше угол наклона, тем больше изменение скорости реакции (рис. 2-15).

Рис. 2-15. Зависимость накопления продукта (А) и убыли субстрата (Б) от времени (продолжительности) протекания реакции. Скорость ферментативной реакции определяется изменением концентрации продукта или субстрата за единицу времени. В реакциях, катализируемых ферментами 1 и 2, начальная скорость реакции, катализируемой ферментом 1, ниже, чем скорость реакции, катализируемой ферментом 2, так как тангенс угла наклона касательной к кривой профиля реакции, проведённой из «0» точки у второго фермента выше, как в случае накопления продукта (А), так и убыли субстрата (Б). Скорость в любой момент времени t определяется тангенсом угла наклона касательной к профилю реакции в момент времени t. Период времени ферментативной реакции [t₀ — t₁] характеризуется линейным накоплением продукта (или убылью субстрата) в зависимости от длительности реакции. Период ферментативной реакции [t₁ — t_x] характеризуется нелинейным накоплением продукта (или убылью субстрата) в зависимости от времени реакции.

С течением времени изменение скорости ферментативной реакции в экспериментальных условиях уменьшается, об этом свидетельствует уменьшение угла наклона касательной в момент времени 1. Снижение скорости ферментативной реакции может происходить за счёт ряда факторов: уменьшения концентрации субстрата, увеличения концентрации продукта, который может оказывать ингибирующее действие, могут происходить изменения pH раствора, инактивация фермента и т. д.

На этапе [t₁— t_x] скорость реакции изменяется нелинейно в зависимости от времени. Поэтому для определения скорости ферментативной реакции чаще всего исследуют изменение скорости на начальном этапе [t₀ — t₁], где наблюдают линейное изменение концентрации продукта (или субстрата).

Скорость ферментативной реакции зависит от ряда факторов, таких как количество и активность ферментов, концентрация субстрата, температура среды, pH раствора, присутствие регуляторных молекул (активаторов и ингибиторов). Рассмотрим влияние этих факторов на скорость ферментативной реакции.

А. Зависимость скорости ферментативной реакции от количества ферментов

При проведении ферментативной реакции в условиях избытка субстрата скорость реакции будет зависеть от концентрации фермента. Графическая зависимость такой реакции имеет вид прямой линии (рис. 2-16). Однако количество фермента часто невозможно определить в абсолютных величинах, поэтому на практике пользуются условными величинами, характеризующими активность фермента: одна международная единица активности (МЕ) соответствует такому количеству фермента, которое катализирует превращение 1 мкмоль субстрата за 1 мин при оптимальных условиях проведения ферментативной реакции. Оптимальные условия индивидуальны для каждого фермента и зависят от температуры среды, pH раствора, при отсутствии активаторов и ингибиторов.

Рис. 2-16. Зависимость скорости ферментативной реакции (V) от концентрации фермента.

Количество единиц активности nМЕ определяют по формуле:

В 1973 г. была принята новая единица активности ферментов: 1 катал (кат), соответствующий такому количеству катализатора, которое превращает 1 моль субстрата за 1 с. Количество каталов определяют по формуле:

Международная единица ферментативной активности МЕ связана с каталом следующими равенствами:

1 кат = 1 моль S/с = 60 моль S/мин = 60 х 10 6 мкмоль/мин = 6 х 10 7 МЕ,

1 МЕ = 1 мкмоль/мин = 1/60 мкмоль/с = 1/60 мккат = 16,67 нкат.

В медицинской и фармацевтической практике для оценки активности ферментов часто используют международные единицы активности — МЕ. Для оценки количества молекул фермента среди других белков данной ткани определяют удельную активность (уд. ак.) фермента, численно равную количеству единиц активности фермента (nМЕ) в образце ткани, делённому на массу (мг) белка в этой ткани:

По удельной активности судят об очистке фермента: чем меньше посторонних белков, тем выше удельная активность.

Б. Зависимость скорости ферментативной реакции от температуры среды

Повышение температуры до определённых пределов оказывает влияние на скорость ферментативной реакции, подобно влиянию температуры на любую химическую реакцию. С повышением температуры ускоряется движение молекул, что приводит к повышению вероятности взаимодействия реагирующих веществ. Кроме того, температура может повышать энергию реагирующих молекул, что также приводит к ускорению реакции. Однако скорость химической реакции, катализируемая ферментами, имеет свой температурный оптимум, превышение которого сопровождается понижением ферментативной активности, возникающим из-за термической денатурации белковой молекулы (рис. 2-17).

Рис. 2-17. Зависимость скорости ферментативной реакции (V) от температуры.

Для большинства ферментов человека оптимальна температура 37— 38 °С. Однако в природе существуют и термостабильные ферменты. Например, Taq — полимераза, выделенная из микроорганизмов, живущих в горячих источниках, не инактивируется при повышении температуры до 95 °С. Этот фермент используют в научно- практической медицине для молекулярной диагностики заболеваний с использованием метода полимеразной цепной реакции (ПЦР).

В. Зависимость скорости ферментативной реакции от рН среды

Активность ферментов зависит от pH раствора, в котором протекает ферментативная реакция. Для каждого фермента существует значение pH, при котором наблюдается его максимальная активность. Отклонение от оптимального значения pH приводит к понижению ферментативной активности.

Влияние pH на активность ферментов связано с ионизацией функциональных групп аминокислотных остатков данного белка, обеспечивающих оптимальную конформацию активного центра фермента. При изменении pH от оптимальных значений происходит изменение ионизации функциональных групп молекулы белка. Например, при закислении среды происходит протонирование свободных аминогрупп (NH₃ + ), а при защелачивании происходит отщепление протона от карбоксильных групп (СОО — ). Это приводит к изменению конформации молекулы фермента и конформации активного центра; следовательно, нарушается присоединение субстрата, кофакторов и коферментов к активному центру. Кроме того, pH среды может влиять на степень ионизации или пространственную организацию субстрата, что также влияет на сродство субстрата к активному центру. При значительном отклонении от оптимального значения pH может происходить денатурация белковой молекулы с полной потерей ферментативной активности.

Оптимум значения pH у разных ферментов различный (рис. 2-18). Ферменты, работающие в кислых условиях среды (например, пепсин в желудке или лизосомальные ферменты), эволюционно приобретают конформацию, обеспечивающую работу фермента при кислых значениях pH. Однако большая часть ферментов организма человека имеет оптимум pH, близкий к нейтральному, совпадающий с физиологическим значением pH (табл. 2-1).

Таблица 2-1. Оптимальные значения pH для некоторых ферментов

Видео:Кинетика. О чем говорят графики. БиохимияСкачать

Кинетика ферментативных реакций

Одним из характерных проявлений жизни является удивительная способность живых организмов кинетически регулировать химические реакции, подавляя стремление к достижению термодинамического равновесия. Ферментативная кинетика занимается исследованием закономерностей влияния химической природы реагирующих веществ (ферментов, субстратов) и условий их взаимодействия (концентрация, рН среды, температуры, присутствие активаторов или ингибиторов) на скорость ферментативной реакции. Главной целью изучения кинетики ферментативных реакций является получение информации, которая может способствовать выяснению молекулярного механизма действия фермента.

Общие принципы кинетики химических реакций применимы и к ферментативным реакциям. Известно, что любая химическая реакция характеризуется константой термодинамического равновесия. Она выражает состояние химического равновесия, достигаемого системой, и обозначается К_р. Так, для реакции:

Рис. 4.12. Теоретический график зависимости скорости ферментативной реакции от концентрации субстрата при постоянной концентрации фермента.

а — реакция первого порядка (при [ S ]

Таким образом, константа равновесия равна отношению констант скоростей прямой и обратной реакций. Величину, обратную константе равновесия, принято называть субстратной константой, или, в случае ферментативной реакции, константой диссоциации фермент–субстратного комплекса, и обозначать символом K_S. Так, в реакции

т.е. K_Sравна отношению произведения концентрации фермента и субстрата к концентрации фермент-субстратного комплекса или отношению констант скоростей обратной и прямой реакций. Следует отметить, что константа K_Sзависит от химической природы субстрата и фермента и определяет степень их сродства. Чем ниже значение K_S, тем выше сродство фермента к субстрату.

При изучении кинетики ферментативных реакций следует учитывать одну важную особенность этих реакций (не свойственную обычным химическим реакциям), связанную с явлением насыщения фермента субстратом. При низкой концентрации субстрата зависимость скорости реакции от концентрации субстрата (рис. 4.12) является почти линейной и подчиняется кинетике первого порядка. Это означает, что скорость реакции S —> Р прямо пропорциональна концентрации субстрата S и в любой момент времени t определяется следующим кинетическим уравнением:

где [S] – молярная концентрация субстрата S; –d[S]/dt – скорость убыли субстрата; k’ – константа скорости реакции, которая в данном случае имеет размерность, обратную единице времени (мин –1 или с –1 ).

При высокой концентрации субстрата скорость реакции максимальна, становится постоянной и не зависящей от концентрации субстрата [ S ] . В этом случае реакция подчиняется кинетике нулевого порядка v = k» (при полном насыщении фермента субстратом) и целиком определяется концентрацией фермента. Различают, кроме того, реакции второго порядка, скорость которых пропорциональна произведению концентраций двух реагирующих веществ. В определенных условиях при нарушении пропорциональности говорят иногда о реакциях смешанного порядка (см. рис. 4.12).

Изучая явление насыщения, Л. Михаэлис и М. Ментен разработали общую теорию ферментативной кинетики. Они исходили из предположения, что ферментативный процесс протекает в виде следующей химической реакции:

т.е. фермент Е вступает во взаимодействие с субстратом S с образованием промежуточного комплекса ES, который далее распадается на свободный фермент и продукт реакции Р. Математическая обработка на основе закона действующих масс дала возможность вывести уравнение, названное в честь авторов уравнением Михаэлиса–Ментен, выражающее количественное соотношение между концентрацией субстрата и скоростью ферментативной реакции:

Из уравнения Михаэлиса–Ментен следует, что при высокой концентрации субстрата и низком значении K_Sскорость реакции является максимальной, т.е. v = V_max(реакция нулевого порядка, см. рис. 4.12). При низкой концентрации субстрата, напротив, скорость реакции оказывается пропорциональной концентрации субстрата в каждый данный момент (реакция первого порядка).

Следует указать, что уравнение Михаэлиса–Ментен в его классическом виде не учитывает влияние на скорость ферментативного процесса продуктов реакции, например в реакции

и носит несколько ограниченный характер. Поэтому были предприняты попытки усовершенствовать его. Так, было предложено уравнение Бриггса-Холдейна:

где К_m представляет собой константу Михаэлиса, являющуюся экспериментально определяемой величиной. Она может быть представлена следующим уравнением:

Рис. 4.13. Кривая уравнения Михаэли-са-Ментен: гиперболическая зависимость начальных скоростей катализируемой ферментом реакции от концентрации субстрата.

В числителе представлены константы скоростей распада комплекса ES в двух направлениях (в сторону исходных Е и S и в сторону конечных продуктов реакции Е и Р). Отношение k_–1/ k₊₁представляет собой константу диссоциации ферментсубстратного комплекса K_S, тогда:

Отсюда вытекает важное следствие: константа Михаэлиса всегда больше константы диссоциации фермент-субстратного комплекса K_Sна величину

Для определения численного значения К_m обычно находят ту концентрацию субстрата, при которой скорость ферментативной реакции v составляет половину от максимальной V_max, т.е. если v = 1 /₂ V_maх. Подставляя значение v в уравнение Бриггса–Холдейна, получаем:

разделив обе части уравнения на V_mах, получим

Таким образом, константа Михаэлиса численно равна концентрации субстрата (моль/л), при которой скорость данной ферментативной реакции составляет половину от максимальной.

Определение величины К_m имеет важное значение при выяснении механизма действия эффекторов на активность ферментов и т.д. Константу Михаэлиса можно вычислить по графику (рис. 4.13). Отрезок на абсциссе, соответствующий скорости, равной половине максимальной, будет представлять собой К_m.

Пользоваться графиком, построенным в прямых координатах зависимости начальной скорости реакции v₀ от начальной концентрации субстрата [S₀], неудобно, поскольку максимальная скорость V_maxявляется в данном случае асимптотической величиной и определяется недостаточно точно.

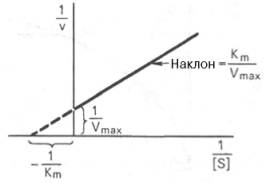
Рис. 4.14. График Лайнуивера-Бэрка.

Для более удобного графического представления экспериментальных данных Г. Лайнуивер и Д. Бэрк преобразовали уравнение Бриггса–Хол-дейна по методу двойных обратных величин исходя из того принципа, что если существует равенство между двумя какими-либо величинами, то и обратные величины также будут равны. В частности, если

то после преобразования получаем уравнение:

которое получило название уравнения Лайнуивера–Бэрка. Это уравнение прямой линии: у = ах + b. Если теперь в соответствии с этим уравнением построить график в координатах 1/v (y) от l/[S] (x), то получим прямую линию (рис. 4.14), тангенс угла наклона который будет равен величине K_m/V_max; отрезок, отсекаемый прямой от оси ординат, представляет собой l/V_max(обратная величина максимальной скорости). Если продолжить прямую линию за ось ординат, тогда на абсциссе отсекается отрезок, соответствующий обратной величине константы Михаэлиса – 1/К_m (см. рис. 4.14). Таким образом, величину К_m можно вычислить из данных наклона прямой и длины отрезка, отсекаемого от оси ординат, или из длины отрезка, отсекаемого от оси абсцисс в области отрицательных значений.

Следует подчеркнуть, что значения V_max, как и величину К_m, более точно, чем по графику, построенному в прямых координатах, можно определить по графику, построенному по методу двойных обратных величин. Поэтому данный метод нашел широкое применение в современной энзимологии. Предложены также аналогичные графические способы определения К_m и V_maxв координатах зависимости v от v/[S] и [S]/v от [S].

Следует отметить некоторые ограничения применения уравнения Ми-хаэлиса–Ментен, обусловленные множественными формами ферментов и аллостерической природой фермента. В этом случае график зависимости начальной скорости реакции от концентрации субстрата (кинетическая

Рис. 4.15. Сигмоидная кинетическая кривая насыщения субстратом.

кривая) имеет не гиперболическую форму, а сигмоидный характер (рис. 4.15) наподобие кривой насыщения гемоглобина кислородом. Это означает, что связывание одной молекулы субстрата в одном каталитическом центре повышает связывание субстрата с другим центром, т.е. имеет место кооперативное взаимодействие, как и в случае присоединения кислорода к 4 субъединицам гемоглобина. Для оценки концентрации субстрата, при которой скорость реакции составляет половину максимальной, в условиях сигмоидного характера кинетической кривой обычно применяют преобразованное уравнение Хилла: