В книжной версии
Том 1. Москва, 2005, стр. 246-248
Скопировать библиографическую ссылку:
АДСО́РБЦИЯ (от лат. ad – на и sorbeo – поглощать), поглощение вещества из газовой фазы или жидкого раствора поверхностным слоем твёрдого тела или жидкости. Явление А. вызывается наличием адсорбц. cилового поля, создаваемого за счёт нескомпенсированности межмолекулярных cил в поверхностном слое. Вещество, создающее такое поле, называется адсорбентом, вещество, молекулы которого могут адсорбироваться, – адсорбтивом, уже адсорбиров. вещество – адсорбатом. Процесс, обратный А., – десорбция. А. – частный случай сорбции . Применение адсорбц. процессов датируется кон. 18 в., когда независимо и практически одновременно появились три публикации: итал. натуралист Ф. Фонтана и К. Шееле в 1777 описали поглощение газов древесным углем, в 1785 Т. Е. Ловиц обнаружил способность таких углей обесцвечивать растворы винных кислот, поглощая органич. примеси.
Видео:Адсорбция (Киевнаучфильм)Скачать
Экология СПРАВОЧНИК
Видео:Адсорбция на твёрдой поверхностиСкачать

Информация
Добавить в ЗАКЛАДКИ
| Поделиться: | Видео:5.1. Адсорбция. Классификация адсорбцииСкачать  Кинетика адсорбцииКинетика адсорбции, или скорость установления адсорбционного равновесия, определяется диффузией вещества в окружающей сорбент среде (внешняя диффузия), диффузией адсорбируемого вещества внутрь зерна (кнудсеновского типа — внутрь пор и фольмеровского — по стенкам пор) и, наконец, кинетикой самого акта адсорбции.[ . ] Кинетику процесса адсорбции определяет наиболее медленно протекающая стадия. При отсутствии перемешивания это может быть первая стадия; при обеспечении достаточной турбулентности кинетика адсорбции может определяться внутридиффузионным переносом сорбата. Собственная адсорбция, по-видимому, не лимитирует скорость процесса. На скорость адсорбции влияют также размер зерен угля, скорость потока воды через угольную загрузку, концентрация загрязнений, температура, реакция среды.[ . ] Влияние кинетики адсорбции ВМС частицами на степень флокуляции проявляется в зависимости от эффективности проведения процесса смешения полимера с дисперсией, от продолжительности и интенсивности перемешивания системы и т. п. Улучшение условий для диффузии макромолекул к поверхности частиц (увеличение продолжительности контакта ВМС с частицами, перемешивание, разбавление дисперсии и др.) приводит, как правило, к росту степени флокуляции. Формирование на частицах достаточно толстого адсорбционного слоя увеличивает «диаметр столкновения », что также может быть причиной увеличения скорости флокуляции по сравнению с коагуляцией электролитом [134], как это было обнаружено при флокуляции положительного золя Agi полиакриловыми кислотами [142].[ . ] Для расчета кинетики адсорбции предложен ряд формул [429, 430], применимость которых оценивается обычно методом подбора на ЭВМ.[ . ] Тимофеев Д. П. Кинетика адсорбции. М., Изд-во АН СССР, 1962.[ . ] Расчет динамики адсорбции растворенных веществ в неподвижном плотном слое активного угля. Теоретическая модель неравновесной динамики адсорбции в неподвижном плотном слое включает уравнения баланса массы, кинетики адсорбции, изотермы адсорбции и соответствующие краевые условия.[ . ] Чтобы определить кинетику адсорбции, берут три образца АУ по 660 мг и помещают в колбы с притертыми пробками со 150 см3 изучаемой воды, которые встряхивают непрерывно с малой интенсивностью в течение 305 с, 40 и 355 мин, соответственно. При этом образец АУ, помещенный в колбу последним, извлекают первым через 305 с. Воду и АУ анализируют.[ . ] При рассмотрении кинетики флокуляции следует различать два аспекта: собственно кинетику агрегации частиц полимером и кинетику адсорбции ВМС (т. е. учет скорости диффузии макромолекул к поверхности и достижения адсорбционного равновесия), являющейся первой стадией процесса флокуляции.[ . ] Физической моделью кинетики адсорбции в неподвижном слое поглотителя, — называемой также динамикой адсорбции, является модель фронтальной отработки слоя адсорбента. В соответствии с этой моделью концентрация целевого компонента, непрерывно поступающего в слой с газовым потоком, прогрессивно увеличивается во времени в первых (лобовых) участках слоя адсорбента, достигая состояния насыщения. Это приводит к уменьшению движущей силы процесса на данных участках и поступлению газа с высокой концентрацией целевого компонента в следующие за лобовыми участками слоя. С другой стороны, при достаточной длине слоя в нем в течение определенного времени будут существовать концевые участки, в которые поступает очищенный газовый поток. Таким образом, в слое адсорбента на некоторой стадии процесса формируется и затем перемещается по слою участок конечной длины I, являющийся работающим слоем (зоной массопередачи), на котором происходит резкое изменение концентрации целевого компонента в проходящем газовом потоке, характеризующееся определенной формой концентрационной кривой (фронта сорбции, сорбционной волны). Ввиду конечной скорости адсорбции форма этой кривой в лобовом участке слоя постоянно изменяется до момента насыщения данного участка. После этого момента при условии сохранения сформировавшихся условий образования концентрационной кривой последняя перемещается вдоль слоя с постоянной скоростью, обеспечивая режим так называемого параллельного переноса адсорбционного фронта.[ . ] Поскольку внутридиффузионная кинетика адсорбции зависит от квадрата радиуса частиц, переход к порошкообразным, углям позволяет значительно сократить необходимое время контакта воды с адсорбентом и соответственно уменьшить объем адсорбционных сооружений.[ . ] Длина зоны массопередачи определяется кинетикой адсорбции, скоростью фильтрования и условиями перемешивания. Поэтому в аппаратах с идеальным вытеснением жидкой фазы (фильтрах с плотным слоем) при прочих равных условиях ¿мп минимальна, в аппаратах с интенсивной продольной диффузией (кипящий слой) ¿мп максимальна.[ . ] Существуют различные способы описания кинетики массообмена при адсорбции, положенные в основу расчетов процессов адсорбционной газоочистки. Один из наиболее простых, доступных и наглядных способов — физическое моделирование кинетики адсорбции, базирующееся на модели фронтальной отработки адсорбента.[ . ] Рассмотрим методы расчета внутридиффузионной кинетики адсорбции органических загрязнений из биологически очищенных сточных вод. По нашим» оценкам, величина эффективного уменьшения дифференциальной мольной свободной энергии адсорбции органических загрязнений из ряда бытовых и промышленных сточных вод равна 16,5 кДж/моль. Для веществ, которые адсорбируются активным углем с близкими к этой величине значениями —Д.Р, показано, что внутридиффузионная кинетика адсорбции в основном определяется миграцией адсорбированных молекул в микропорах активного угля [19]. При этом внутридиффузионную кинетику адсорбции такой сложной смеси можно рассчитывать по модели (У-15) для такого растворенного вещества, ХПК которого равно ХПК смеси органических загрязнений. Величина коэффициента Оа в этом случае имеет порядок Ю-® см2/с [37].[ . ]
Исследование динамики сорбции из растворов на угле [36] показало удовлетворительное соответствие с теорией динамики сорбции газов, основанной на статике и кинетике сорбции и гидродинамике потока сквозь слой зерненного материала (теория ЖЗТ) [35]. Как было установлено при изучении роли внутреннего (внутри зерна), внешнего (от раствора к зерну) и продольного (между зернами) переноса в случае динамической адсорбции уксусной и масляной кислот из водных растворов [37], значение продольного переноса очень мало. При удельных скоростях потока от 0,036 до 0,29 см/сек в кинетике адсорбции доминирующую роль играет внешний перенос. В случае адсорбции уксусной кислоты из растворов малой концентрации (7 ммоль/л) при скорости 3 см/сек на зернах диаметром 0,375 см и при скорости 8 см/сек на зернах диаметром 0,25 см, а также при дальнейшем увеличении скорости тока или диаметра зерен угля основная роль переходила к внутреннему переносу. При больших концентрациях кислоты (30 ммоль/л) скорость адсорбции всегда зависела от внутреннего переноса.[ . ] При изучении виутридиффузионного процесса необходимо учитывать особенности пористой структуры сорбентов. В некоторых активных углях (КАД, АГ-3, СКТ) поры с различной энергией адсорбции образуют в грануле угля сплошные структуры, причем поры каждого вида выходят на поверхность зерна. Для углей с такой структурой развиты представления о параллельном массопереносе адсорбированных и неадсорбирован-ных молекул внутри гранулы [19, 20]. Хорошее согласование экспериментальных кинетических кривых с данными расчетов по такой модели свидетельствует о корректности ее применения к изучению кинетики адсорбции растворенных веществ на активных углях [19, 21—24].[ . ] Следует отметить, что коэффициент Зг , входящий в уравнение (У-32), практически не зависит от концентрационных факторов. В то же время использование уравнения (У-31) для количественного описания внутридиффузионной кинетики адсорбции связано с необходимостью учета зависимости коэффициеп та от заполнения, что существенно осложняет теоретическую сторону исследования.[ . ] Для выявления характера распределения концентраций поглощаемого-вещества в газовой фазе и в слое адсорбента в данный момент времени необходимо в общем случае составить и решить при соответствующих начальных и граничных условиях систему уравнений материального баланса, изотермы и кинетики адсорбции, гидродинамики процесса. Решение такой системы уравнений возможно лишь путем их упрощения за счет введения ряда допущений и приближений, рассмотрения частных, наиболее простых случаев динамики адсорбции.[ . ] Величина 50 определяется по методике, описанной в [14]. Соотношение ( М2) можно использовать для расчета коэффициентов массоотдачи при адсорбции смеси двух веществ из разбавленных растворов. Теоретическая модель внешнедиффузионной кинетики адсорбции смеси двух органических веществ из водных растворов рассмотрена в [15].[ . ] Формула Н. А. Шилова отражает влияние статического к и кинетического ¿о факторов на динамику поглощения слоем. При решении ряда технологических задач необходимо знать степень отработки адсорбционной емкости в данном сечении слоя в заданный момент времени, распределение концентрации вещества в подвижной фазе по высоте слоя, и т. д. Эти характеристики могут быть получены на основе теоретической модели неравновесной динамики адсорбции, позволяющей выявить влияние кинетики адсорбции на работу адсорбционной колонны.[ . ] Величины £)а можно также рассчитать сопоставлением экспериментальной кинетической кривой с теоретически рассчитанной, являющейся решением исходной системы уравнений (У-15). Данные такого сопоставления, проведенного нами, свидетельствуют о том, что Б а в пределах одного кинетического опыта удовлетворительно описывается моделью с постоянной величиной йа [уравнения (У-15)] вплоть до относительно высокой степени приближения к равновесию. Измерение кинетики адсорбции одного и того же вещества на данном адсорбенте при различных начальных и конечных состояниях системы, показало, что величина Х) а несколько изменяется от опыта к опыту.[ . ] Видео:Химия. 9 класс (Урок№17 - Углерод. Аллотропные модификации углерода.Химические свойства. Адсорбция.)Скачать  Кинетика процесса адсорбцииПереход вещества из объемной фазы в адсорбированное состояние и удаление его из адсорбированного состояния являются диффузионными процессами. Механизм переноса зависит от характера пористости сорбента и условий протекания процесса. В реальных пористых сорбентах, имеющих сложную структуру, процесс переноса происходит различными путями, что осложняет теоретический анализ кинетики процесса в целом. Перенос вещества в порах адсорбента посредством диффузии изучает кинетика адсорбции и десорбции. Особое значение имеет кинетика химического поглощения газов твердыми сорбентами с образованием поверхностных и объемных соединений. В этом случае эффективность процесса обусловлена обеспечением высоких кинетических параметров, максимальной удельной скоростью взаимодействия, интенсивной диффузией внутри зерен, высокой степенью использования материала в реакции. Диффузионные процессы в гомогенной среде описываются законами Фика. Первый закон Фика характеризует стандартную одномерную диффузию, то есть диффузию, протекающую в одном направлении с постоянным во времени градиентом концентрации. Уравнение I закона Фика имеет вид: где G – количество диффундирующего вещества; D – коэффициент диффузии; F – поверхность, перпендикулярная направлению диффузии; c – концентрация адсорбтива в газовой фазе; x – координата направления, в котором происходит диффузия; Второй закон Фика характеризует нестационарную одномерную диффузию и описывается уравнением: где a – концентрация адсорбата, величина адсорбции; Dс – эффективный коэффициент диффузии. С помощью первого закона Фика описывают, например, механизм переноса адсорбата в транспортных порах, где можно экспериментально обеспечить стационарность процесса. При диффузии, сопровождающейся адсорбцией, концентрация сорбата в твердой фазе изменяется, градиент концентрации изменяется и процесс упрощенно можно описать вторым законом Фика. На кинетику процесса адсорбции оказывает влияние пористая структура адсорбента. В том случае, когда основной вклад в сопротивление диффузии вносят микропоры, большое влияние на кинетику адсорбции оказывает диаметр кристаллита. Разнообразие структуры определяет особенности переноса вещества в грануле. Вид переноса может быть охарактеризован на основании зависимости коэффициента диффузии от давления, температуры, молекулярного веса сорбата, газа–носителя. В крупных порах, когда диаметр пор больше средней длины свободного пробега молекул адсорбтива, преимущественным видом переноса является нормальная или объемная диффузия. Скорость нормальной диффузии определяется числом столкновений молекул газа друг с другом. Коэффициент диффузии в этом случае зависит от средней тепловой скорости молекул (U) и средней длины свободного пробега молекул (λ): Величины U, λ возрастают при повышении температуры. Коэффициент диффузии соответственно связан с температурой: При малом размере пор, когда длина свободного пробега молекул много больше размера пор, скорость диффузии определяется числом соударений со стенками пор. Такая диффузия называется молекулярной или кнудсеновской. При столкновении адсорбирующихся молекул с поверхностью они некоторое время оказываются зафиксированными активными центрами адсорбента, после чего могут вновь вернуться в газовую фазу под влиянием теплового движения. Коэффициент молекулярной диффузии зависит от средней скорости движения молекул (U) и диаметра пор (dn): с температурой он связан зависимостью: Если пора по размерам соизмерима с поглощаемыми молекулами, адсорбционный процесс приобретает активированный характер, то есть проникают в поры и адсорбируются там лишь те молекулы, которые обладают некоторой величиной избыточной энергии – энергией активации. Коэффициент диффузии связан с энергией активации (Eа) зависимостью: Величины D0 экспериментально устанавливаются и табулируются для различных адсорбентов и адсорбтивов. Энергия активации при адсорбции резко возрастает по мере снижения определяющего размера пор до критического диаметра молекул, то есть энергия активации может использоваться как молекулярно-ситовая характеристика адсорбентов. У сорбентов с ионообменной способностью энергия активации зависит также от радиуса и размера иона, входящего в состав сорбента. Например, энергия активации у ионообменных форм морденита (цеолит) возрастает при переходе от Li- к Na- форме, а затем при переходе к K- и NH4— форме уменьшается. Интенсивность переноса вещества в гранулах промышленных адсорбентов усиливается благодаря миграции молекул по поверхности пор – поверхностной диффузии. По поверхности молекулы движутся скачкообразно. Коэффициент поверхностной диффузии зависит от времени пребывания молекулы в адсорбированном состоянии (τ) и длины скачка молекулы (∆): Величина где τ0 – период колебания атомов в структуре адсорбентов (≈ 10 -13 с) Коэффициент поверхностной диффузии зависит от температуры: При повышении температуры роль поверхностной диффузии в общей скорости переноса вещества падает. 🎥 ВидеоПостроение изотермы адсорбцииСкачать  АдсорбцияСкачать  Поверхностные явления. Адсорбция.Скачать  Адсорбция на поверхностях растворовСкачать  АдсорбцияСкачать  Поиск формулы вещества по продуктам его сгоранияСкачать  Уравнение ЛенгмюраСкачать  Экзо- и эндотермические реакции. Тепловой эффект химических реакций. 8 класс.Скачать  Как выучить Химию с нуля за 10 минут? Принцип Ле-ШательеСкачать  Поверхностные явленияСкачать  Коробов М. В. - Физическая химия. Часть 1 - Адсорбция на границе газ-твердое. Модель ЛенгмюраСкачать  Динамические уравнения ЭйлераСкачать  Ректификационная колонна принцип работыСкачать  СорбцияСкачать  Поверхностные явленияСкачать  Поверхностные явления. Адсорбция на подвижных границах раздела фаз.Скачать  |






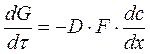 ,
,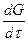 – скорость диффузии;
– скорость диффузии;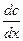 – градиент концентрации в направлении протекающей диффузии.
– градиент концентрации в направлении протекающей диффузии.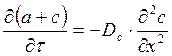 ,
,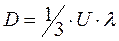 .
.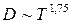 .
.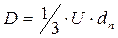 ;
;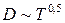 .
.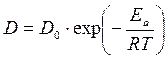 .
.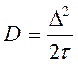 .
.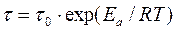 ,
,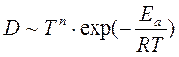 , n = 0,5÷1,5
, n = 0,5÷1,5