Кинетическое уравнение для реакции третьего порядка (3 видео)

Содержание

Реакции третьего порядка
Кинетическое уравнение для реакции третьего порядка
Константа скорости химической реакции. Энергия активации
И.М. Эммануэль, Д.Г. Кнорре.
Кинетическое уравнение для реакции третьего порядка
🔍 Видео

Видео:Влияние концентрации на скорость химических реакций. 10 класс.Скачать

Реакции третьего порядка

При равных начальных концентрациях реагентов в общем виде кинетическое уравнение реакции третьего порядка

или –dc/с 3 = k·dτ.

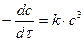
После интегрирования получаем:

где В – постоянная интегрирования.

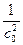
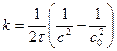
При τ = 0 В = . Тогда

. (94)

Константу скорости реакции третьего порядка измеряют в дм 6 /(моль 2 ·время).

. (95)

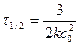
Для реакции третьего порядка период полупревращения обратно пропорционален квадрату начальной концентрации реагентов.

Порядок реакции определяют несколькими способами, используя опытные данные об изменении концентрации реагирующих веществ со временем.

1. Метод подстановки. Экспериментально находят концентрацию одного из веществ через определённые промежутки времени от начала реакции. Подставляют найденные значения концентрации в уравнения (88), (90), (92), (94) и рассчитывают значения константы скорости. Уравнение, дающее одинаковые значения константы скорости в различные моменты времени, указывает на порядок реакции.

2. Графический метод. Из приведённых уравнений следует, что зависимость концентрации от времени для различных порядков может быть выражена прямой линией в соответствующей системе координат: с – τ (для n=0), lnс – τ (для n=1), 1/с – τ (для n=2), 1/с 2 – τ (для n=3). Отложив на оси абсцисс время τ, а на оси ординат – с, lnс, 1/с, 1/с 2 , для изучаемой реакции получают четыре линии. Система координат, в которой экспериментальные данные лягут на прямую линию, укажет на порядок реакции, а тангенс угла наклона прямой к оси абсцисс равен константе скорости k (дляn=0,1,2) или 2 k (для n=3).

3. По периоду полупревращения. Период полупревращения для реакций различного порядка по-разному зависит от начальной концентрации реагентов (уравнения (89). (91), (93), (95)). Для реакции нулевого порядка τ_1/2 прямо пропорционален начальной концентрации с₀, для реакции первого порядка – не зависит от начальной концентрации с₀, для реакции второго порядка – обратно пропорционален с₀, для реакции третьего порядка – обратно пропорционален с 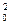. Проводят опыты с различными начальными концентрациями реагентов, находят τ_1/2 и делают вывод о порядке реакции.

Дата добавления: 2014-12-07 ; просмотров: 3626 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Физическая химия #3. Первый, второй и третий порядки химической реакции. Времена полупревращенияСкачать

Кинетическое уравнение для реакции третьего порядка

Константа скорости химической реакции. Энергия активации

И.М. Эммануэль, Д.Г. Кнорре.

Источник:И.М. Эммануэль, Д.Г. Кнорре. Курс химической кинетики, изд. «Высшая школа», 1979, с.73-76.

При заданных внешних условиях (температура, давление, среда, в которой происходит процесс) скорость химического превращения является функцией только концентраций компонентов реакционной смеси. Уравнение, описывающее зависимость скорости химического процесса от концентрации компонентов реакционной смеси, называется кинетическим уравнением химического процесса.

Очень часто в химической кинетике приходится иметь дело с процессами, скорость которых оказывается пропорциональной произведению концентраций реагирующих веществ в соответствующих степенях.

Если зависимость скорости реакции от концентрации реагирующих веществ записывается в виде

(1)

то величины n_i (i = I, 2, . I) принято называть порядком реакции по веществу А_i.

Сумму порядков реакции по всем реагирующим веществам называют порядком реакции. Множитель и в кинетическом уравнении (1), показывающий, с какой скоростью идет химический процесс при концентрациях реагирующих веществ, равных единице, называется константой скорости химического процесса. Наряду со скоростью константа скорости химического процесса является основной величиной в химической кинетике.

Степенная зависимость скорости реакции от концентраций реагирующих веществ (1) практически всегда выполняется для скорости отдельных стадий химического процесса. При этом как порядок по отдельному компоненту, так и суммарный порядок реакции являются целыми положительными числами. Для отдельной стадии порядок реакции никогда не превышает трех. Поэтому особо важное значение в химической кинетике имеют реакции первого, второго и третьего порядка.

Константы скорости реакций различного порядка имеют разную размерность. Поскольку размерность скорости реакции независимо от кинетического уравнении этой реакции есть [С] [t] -1 , то из (1) следует, что размерность константы скорости для реакции первого порядка [t] -1 , второго порядка [С] -1 [t] -1 , третьего порядка [С] -2 [t] -2 .

В соответствии с этим единицами измерения констант скорости являются:

для реакции первого порядка: с -1
для реакции второго порядка: м 3 /молекула &#183 с (м 3 &#183 с -1 ) или М -1 &#183 с -1 [л/(моль &#183 с)]
для реакции третьего порядка: м 6 /молекула 2 &#183 с (м 6 &#183 с -1 ) или М -2 &#183 с -1 [л 2 /(моль &#183 с)]

При использовании молярных единиц для выражения концентрации при расчетах в системе единиц СИ следует помнить, что это эквивалентно использованию единиц кмоль/м 3 , и поэтому все остальные величины, относимые к определенному количеству вещества (универсальная газовая постоянная, число Авогадро), должны также браться в расчете на 1 киломоль.

Следует подчеркнуть, что константы скорости реакций разных порядков являются разными физическими величинами и сопоставление их абсолютных значений лишено какого бы то ни было смысла. При переходе от одной единицы измерения концентрации к другой константа скорости реакции первого порядка не изменяется, константа скорости реакции второго порядка изменяется в 6,02 &#183 1026 раз, а константа скорости реакции третьего порядка — в 3,6 &#183 1053 раз.

Константа скорости химической реакции, как правило, резко растет с повышением температуры. Зависимость константы скорости реакции от температуры в большом числе случаев может быть описана уравнением Аррениуса

(2)

где Т — абсолютная температура; k₀ и Е — постоянные параметры.

Поскольку концентрация реагирующих веществ практически не зависит от температуры, то такое же соотношение получается и для скорости процесса

(3)

где

Относительное увеличение скорости реакции с температурой характеризуется логарифмической производной &#965 по Т:

(4)

Таким образом, чем больше Е, тем быстрее растет скорость реакции с температурой. Для простых реакций параметр Е показывает, какой минимальной энергией (в расчете на один моль) должны обладать реагирующие частицы, чтобы они могли вступить в химическую реакцию. Частицы, энергия которых больше или равна Е, называются активными, а параметр Е в связи с этим называют энергией активации.

Для сложных реакций, состоящих из нескольких стадий, параметр Е в уравнении (2), как правило, не имеет такого простого физического смысла и является некоторой функцией энергии активации отдельных стадий. Тем не менее и в этом случае параметр. Е принято называть энергией активации, хотя правильнее было бы называть его эффективной или эмпирической энергией активации.

Параметр k₀ называется предэкспоненциальным множителем.

Параметры Е и k₀ могут быть определены из зависимости константы скорости реакции от температуры с помощью уравнения (2), записанного в виде

(5)

Видео:Порядок реакцииСкачать

Кинетическое уравнение для реакции третьего порядка

Из уравнений (4) и (5) видно, что критериями первого порядка реакции по реагенту А является линейная зависимость ln [ A ] – t или ln – t

В тоже время по тангенсам углов наклона линейных зависимостей можно определить константы скорости.

Другой тест правильности выбранного первого порядка является постоянство константы скорости реакции, вытекающее из уравнения (5)

Размерность константы скорости первого порядка dim = [1/ c ], [1/мин] или соответственно с -1 , мин -1

Третий тест основан на концентрационной зависимости времени полупревращения. Условие полупревращения [ A ] = 0,5[ A ]₀ , тогда в соответствии с уравнением (5)

Можно видеть, что критерием первого порядка реакции является независимость времени полупревращения t _½ от начальной концентрации реагента [ A ]₀.

Примерами подобных реакций первого порядка являются реакции изомеризации, а также реакции разложения некоторых сложных молекул в газовой фазе.

и в жидкой фазе, например, гидролиз трет-бутилбромида.

Для реакции A + B → C + D можно записать уравнение скорости

Обозначим [ A ]₀ и [ B ]₀ – начальными концентрациями реагентов А и В, а Х – количество прореагировавших А и В, тогда уравнение (1) приобретет вид

Разделяя переменные, имеем

Проинтегрируем левую часть этого уравнения методом неопределенных коэффициентов, для чего представим дробь

в виде суммы дробей

Решая совместно эти уравнения, имеем

Подставляя значения α и β в уравнение (3) и (4) и интегрируя полученные уравнения в соответствующих пределах

Из уравнения (5) видно, что критерием правильности выбранного второго порядка реакции является линейность зависимости

от времени.

По тангенсу угла наклона этой зависимости можно определить константу скорости реакции. Другим критерием правильности выбранного второго порядка является постоянство значений k , вычисленных в соответствии с уравнением (5):

во всем диапазоне пар значений τ – х.

Размерность константы скорости второго порядка

или, соответственно, л·моль -1 ·с -1 , л·моль -1 ·мин -1 .

Если вещества А и В взяты в равных количествах или реакция идет с участием одного вещества, например

то при постоянстве объема удобно использовать в качестве переменной концентрацию одного из исходных веществ

тогда кинетическое уравнение будет иметь вид

Интегрируя это уравнение в соответствующих пределах

приходим к выражению

Из уравнений (7) и (8) следует, что критериями правильности выбранного второго порядка являются линейный характер зависимости 1/[ A ] от t и постоянство значения k , вычисленных для различных пар значений [ A ] – t по формуле

Третий критерий правильности второго порядка основан на определении времени полупревращения t _½ _. Так как [ A ] = 0.5[ A ]₀, то в соответствии с уравнением (7)

, откуда

Можно видеть, что критерием второго порядка является обратно пропорциональная зависимость между t _½ и начальной концентрацией реагента. В соответствии с выражениями (7) и (8) константы скорости второго порядка можно определить по тангенсу угла наклона зависимостей или от времени.

Имеется множество реакций протекающих по кинетике второго порядка:

и простой случай, соответствующий равенству исходных и текущих концентраций реагентов

Разделяя переменные и интегрируя

Из уравнения (3) видно, что критериями правильности выбранного третьего порядка является линейность зависимостей или от t , постоянства значения k , вычисленное по формуле

для всех пар значений t и [ A ] и обратно пропорциональная зависимость между временем полупревращения и квадратом начальной концентрации реагента

В соответствии с уравнением (3) константа скорости третьего порядка может быть определена по тангенсу угла наклона зависимости или от времени.

Интегрирование уравнения (1)

приводит к выражениям

Из уравнений (2) и (3) следует, что критериями нулевого порядка по реагенту А являются линейный характер зависимости [ A ] от t , постоянство k , вычисленного по формуле

во всем диапазоне пар значений t – A и прямолинейная зависимость между временем полу превращения и начальной концентрацией реагента

Из уравнений (2) и (3) следует, что константа скорости нулевого порядка может быть определена по тангенсу угла наклона зависимостей [ A ]₀ – [ A ] или [ A ] от времени

Сложные реакции представляют собой совокупность простых реакций. К сложным реакциям относятся обратимые реакции.

При кинетическом анализе сложных реакций руководствуются принципом независимости простых реакций, согласно которому каждая простая реакция, входящая в сложную ведет себя кинетически так, как если бы она была единственная.

в начальный момент времени концентрация реагента A составляет [ A ]₀, а [ B ] = 0, то уравнение этой реакции запишется как

Выражая r через концентрацию [A] имеем

= k₁<[A]₀ – X> – k_-1X

где X – количество молей вещества A в единице объеме, которое прореагировало к моменту τ и соответственно количество молей вещества B в единице объеме, которое образовалось к этому моменту. Преобразуя правую часть уравнения (2)

= k₁[A]₀ – (k-₁ + k₁)X

В условиях равновесия

При τ ® ¥ X стремится к своему равновесному значению X ® X _¥ . Тогда

где

Тогда кинетическое уравнение (3) примет вид

Интегрируя это уравнение в соответствующих пределах

В соответствии с выражениями (6) и (7) кинетические зависимости для A и B будут иметь следующий вид

Пользуясь интегральной формой кинетического уравнения (5) и соотношением можно на основе кинетических данных определить значения констант скоростей k ₁ и k _-1

Так, в соответствии с (5)

так как , то

Подставляя последнее выражение в уравнение (8), имеем

Подставляя выражение (10) в уравнение (8), имеем

Рассмотрим систему параллельных реакций первого порядка

В соответствии с ранее принятыми обозначениями суммарная скорость расходования реагента A выразится уравнением

По форме уравнение (1) подобно кинетическому уравнению необратимой реакции первого порядка, поэтому его интегральная форма имеет вид.

Разрешая уравнение (2) относительно [ A ] имеем

Для определения констант k ₁ и k ₂ рассмотрим уравнения конкурирующих параллельных реакций.

Поделив почленно, левые и правые части уравнений (5) и (6), имеем уравнение , интегрирование которого приводит к равенству

Разделяя, левые и правые части уравнений (5) и (1), (6) и (7), приходим к очевидным равенствам

интегрирование которых дает уравнения:

Подставляя в последние уравнения выражение (4) приходим к равенствам

Уравнения (2) и (8) являются основой для определения абсолютных значений констант скорости конкурирующих реакций k ₁ и k ₂ . На первом этапе можно определить сумму констант скоростей k ₁ + k ₂ , пользуясь уравнением (2). Затем на основе линейных зависимостей между X_B и X , а также X_C и X определяют брутто константы и , из которых рассчитывают k ₁ и k ₂ по ранее определенному значению суммарной константы скорости k ₁ + k ₂ .

Нетрудно показать, что для трех параллельных реакций первого порядка

Этот случай более сложен по сравнению с предыдущим. Рассмотрим систему параллельных реакций

Уравнение скорости расхода A в этой системе реакций с учетом его количества, прореагировавшего к моменту времени t (Х) имеет вид:

или с учетом преобразований

обозначая , имеем

Разделяя переменные, приходим к выражению

Интегрируем левую часть уравнения (3) методом неопределенных коэффициентов, для чего представим левую её часть в виде суммы дробей.

или

так как , то и

Тогда и

Откуда и ,

С учетом (4) возвращаемся к уравнению (3)

Интегрирование уравнения (5) приводит к выражению

Откуда

или

Возвращаясь к соотношению преобразуем (6) в равенство

Рассмотрим систему двух последовательных реакций первого порядка

В силу принципа независимости скорости расходования реагента A выражается уравнением скорости необратимой реакции первого порядка

Решение которого дается в виде

, и

Уравнение скорости изменения концентрации промежуточных продуктов

Разделим почленно левые и правые части уравнений (3) и (1)

Уравнение (4) имеет признаки однородного уравнения первого порядка. Для его решения вводим обозначение

Подставляя последнее выражение в уравнение (4), имеем:

Разделяем переменные и интегрируем

тогда

или

Так как , то уравнение (5) можно выразить в форме

В тоже время в соответствии с уравнением (2)

Тогда уравнение (5) можно преобразовать в форму

Выведенные зависимости показывают, что в случае необратимых последовательных реакций уравнение для первого промежуточного продукта связано с характеристиками лишь первых двух стадий, оставаясь одинаковым при любом числе и характеристиках последующих стадий. При этом независимо от начальной концентрации реагента A , значение второй характеристики материального баланса укладывается на одну кривую, если её изображать как функцию Х_А или t .

Используя уравнение (5) можно найти по экспериментальным данным путем подбора и зная, на основе кинетически исчерпывания A величину k ₁ – определить k ₂ .

Из анализа уравнения (6) следует, что при X_A = 0 и X_A = 1 , что говорит о наличии максимума . Его положение можно найти, приравнивая к нулю соответствующую производную

откуда

и значение максимума

Из выражений (8) и (9) видно, что положение и величина максимума промежуточного продукта в необратимых реакциях первого порядка зависит только от соотношения констант скоростей первых двух стадий. При этом, чем больше величина , тем ниже максимум и тем больше его положение смещается в сторону более низких степеней превращения (и наоборот). Очевидно, что по экспериментальному положению максимума можно определить по специальным номограммам или по уравнению (8) значение и использовать его в дальнейшем для описания значений концентраций B во времени согласно уравнению (7)

Уравнение образования продукта C :

Максимальная скорость соответствует точке перегиба на зависимости [ C ] от t и определяется из условия

Легко видеть, что это условие соответствует одновременно условию максимума концентрации B , определяемого уравнениями(8) и (9). Качественно проанализированные зависимости могут быть представлены графически.

Неэлементарные реакции состоят из ряда элементарных стадий, составляющих их механизм. Кинетика таких реакций определяется последовательностью элементарных стадий, их характером (обратимые, необратимые), природой реагентов, интермедиатов и продуктов реакции. При кинетическом анализе неэлементарных реакций возникает задача определения концентраций интермедиатов, играющих ключевую роль в образовании продуктов или расходовании реагентов. В качестве инструмента такого определения используется принцип квазистационарных концентраций Боденштейна – Семенова. Согласно этому принципу скорость изменения концентраций нестабильных интермедиатов пренебрежимо мала по сравнению со скоростью изменения концентраций реагентов и продуктов реакции и её можно считать равной нулю. Применение принципа стационарных концентраций к неэлементарным реакциям, протекающим по сложному механизму, позволяет исключить из кинетического описания процессов неизвестные концентрации интермедиатов и получить одно или некоторый минимум дифференциальных уравнений скорости, выраженных через подлежащие измерению концентрации реагентов и продуктов реакции.

Рассмотрим пример неэлементарной реакции, описываемой стехиометрией

и протекающей через образование интермедиата Q

Скорость реакции можно приравнять к скорости образования продукта B

В соответствии с принципом квазистационарных концентраций

откуда

Подставляя последнее выражение в уравнение (1) приходим к уравнению скорости реакции

Если экспериментально возможно непосредственно измерить скорость реакции, то обработку кинетических данных можно провести, преобразуя уравнение (3) как:

Последнее уравнение приводится к виду

Обрабатывая зависимость (4) в координатах по ординате находят k ₁ , а по тангенсу угла наклона . Полученных констант достаточно для кинетического описания реакции, так как, разделив числитель и знаменатель уравнения (3) на k ₂ , приходят к уравнению