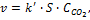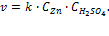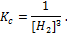Кинетические уравнения скоростей гетерогенной реакции (4 видео)

Содержание

Особенности кинетики гетерогенных реакций
Особенности кинетики гетерогенных реакций
Кинетические уравнения скоростей гетерогенной реакции
📽️ Видео

Видео:Химическая кинетика. Скорость химической реакции | ХимияСкачать

Особенности кинетики гетерогенных реакций

Гетерогенные реакции идут на поверхности раздела фаз, поэтому особенностью кинетики этих реакций является влияние площади реакционной поверхности (S) на скорость реакции.

Если в реакции участвуют твердые или жидкие вещества (не растворы), то их концентрация в кинетическом уравнении, как и в законе действующих масс для равновесия, не учитывается, а константа скорости равна

Например, для реакции

кинетическое уравнение имеет вид:

Гетерогенные реакции являются многостадийными:

1. подвод реагентов к границе раздела;

2. адсорбция на поверхности;

3. химическое взаимодействие (может протекать в несколько элементарных стадий);

4. десорбция продуктов реакции;

5. отвод продуктов реакции от поверхностираздела фаз (диффузия) в объем системы.

Скорость процесса определяется самой медленной стадией. Сказать, какая из стадий будет самой медленной заранее невозможно, так как законы происходящих процессов сильно отличаются друг от друга и их нельзя свести к одному уравнению (виду).

В качестве типичного примера гетерогенной реакции рассмотрим лабораторный метод получения водорода из металлического цинка и разбавленной серной кислоты:

Рис. 3.6Реакции взаимодействия одной крупной или нескольких мелких гранул цинка с серной кислотой.

Цинк в виде гранул (кусочки металла неправильной формы и разной величины) помещают в разбавленный раствор серной кислоты и собирают выделяющийся газообразный водород. В пробирке с одной крупной гранулой реакция идет заметно медленнее (рис. 3.6). При одинаковой массе цинка в пробирках количество выделившегося водорода в обоих опытах будет одинаковым, но в пробирке с мелкими гранулами реакция закончится быстрее. Причина в том, что реакция между цинком и раствором серной кислоты идет только на поверхности контакта гранул с раствором (граница раздела фаз), а общая поверхность у нескольких мелких гранулбольше, чем у одной крупной гранулы той же массы. Цинк в виде порошка для этой реакции использовать просто опасно – реакция начинает идти настолько быстро, что смесь выплескивается из пробирки.Для такой гетерогенной реакции уже нельзя записать кинетическое уравнение вида:

Один из членов этого уравнения – «молярная концентрация цинка» — не имеет смысла, поскольку цинк находится в твердой фазе. Из опыта мы видим, что на скорость гетерогенной реакции влияет степень раздробленности твердого вещества. В принципе, этот фактор может учитываться (чисто экспериментально) константой скорости реакции – тогда для реакций с одной крупной или несколькими мелкими гранулами численные значения k будут разными, а кинетическое уравнение реакции в общем случае примет вид:

Но и такое уравнение не сможет достаточно хорошо описывать скорость данной реакции. Во-первых, в ходе реакции гранулы постепенно уменьшаются в размерах, площадь их поверхности меняется и константа скорости реакции k уже не может учитывать это изменение. Если использовать гранулы из очень чистого цинка, то к ним «прилипает» образующийся водород и площадь контакта реагентов меняется непредсказуемо. Во-вторых, на поверхности раздела фаз концентрация серной кислоты совсем не такая, как в верхних слоях раствора. В зоне реакции активно образуется раствор соли ZnSO₄, который вытесняет раствор серной кислоты с поверхности гранул.

Итак, в общем случае скорость гетерогенной реакции зависит от:

а) скорости подвода реагентов к границе раздела фаз;

б) скорости реакции на поверхности раздела фаз, которая зависит от площади этой поверхности;

в) скорости отвода продуктов реакции от границы раздела фаз.

Химическое равновесие

Многие химические реакции не протекают до конца, то есть исходные реагенты не полностью превращаются в продукты. Такие реакции начинают протекать в одном направлении, затем за счет взаимодействия продуктов реакции идут в обратном направлении, то есть являются двусторонними. Их называют химически обратимыми.

Химические реакции могут быть практически необратимыми и совершенно необратимыми. Например, реакция

практически необратима; лишь при температурах в несколько тысяч градусов вода распадается на Н₂ и О_2. Примером совершенно необратимых реакций является разложение взрывчатых веществ, для которых DS> 0 при DH

Химически обратимые реакции протекают одновременно как в прямом, так и в обратном направлении. В начальный момент времени,при смешении реагентов в смеси концентрация исходных веществ максимальна, а продуктов реакции нет, поэтому скорость прямой реакции имеет наиболее высокое значение, а скорость обратной реакции равна нулю. По мере протекания реакции, концентрация исходных веществ уменьшается, и скорость прямой реакции снижается, а продукты реакции накапливаются, и скорость обратной реакции постепенно возрастает. Обратимый процесс длится до тех пор, пока скорости прямой и обратной реакции не станут равны. Состояние, при котором скорости и прямой, и обратной реакции равны, называется химическим равновесием.

Кинетические уравнения скоростей гетерогенной реакции

Рис. 3.7 Изменение скорости прямой и обратной реакций

с течением времени.

Любая реакция может протекать самопроизвольно только в направлении, которое приближает систему к состоянию равновесия, в котором силы, вызывающие процесс, уравновешиваются.

Химическим равновесиемназывают не изменяющееся во времени при постоянном давлении, объеме и температуре состояние системы, содержащей вещества, способные к взаимодействию.

При некоторой температуре энтальпийный и энтропийный факторы уравниваются, то есть DН = Т . DS. В этом случае DG = 0,что являетсятермодинамическим условием химического равновесия. Существуют различные виды равновесных состояний.

Истинное(устойчивое, термодинамическое) равновесиесистемы характеризуется неизменностью во времени. При этом система изменяет состояние соответственно внешним воздействиям и его характеристики (например, концентрации) не зависят от того, с какой стороны система подходит к равновесию. Устойчивое равновесие является динамическим. Равновесное состояние сохраняется во времени не вследствие отсутствия или прекращения процесса, а вследствие протекания его одновременно в двух противоположных направлениях с одинаковой скоростью.

Кажущееся(метастабильное, заторможенное)равновесиеотличается тем, что для него выполняется только один признак – неизменность во времени. Например, смесь Н₂ и О₂ может практически бесконечно находиться в неизменном, метастабильном состоянии. Однако это не истинное равновесие, так как, раз начавшись (от искры или действия платинового катализатора, который при этом химически не изменяется), процесс взаимодействия идет быстро и практически до конца с выделением тепла:

Количественной характеристикой равновесного состояния является величина, называемая константой равновесия (К). В состоянии равновесия состав системы не меняется, то есть концентрации реагентов и продуктов реакции остаются постоянными (они называются равновесными и обозначаются квадратными скобками).

В 1864 году норвежские ученые К. Гульдберг и П. Вааге сформулировали закон действующих масс:отношение произведения равновесных концентраций продуктов реакции к произведению равновесных концентраций исходных веществ (реагентов) с учетом стехиометрических коэффициентов реакции, при Т = const, является величиной постоянной.Например, для обратимой реакции

закон действующих масс имеет вид:

или, если вещества – газы:

где [A], [В], [C] и [D] – равновесные концентрации веществ (моль/л); p_A, p_B, p_C, p_D – парциальные давления газов.

Например, для реакции

закон действующих масс имеет вид

Если все реагенты газообразны и их поведение подчиняется законам идеальных газов, то связь между К_Р и К_С можно выразить уравнением:

где Δn- изменение числа молей газов в результате реакции; так что для рассматриваемой реакции

и .

Константа равновесия обладает тем свойством, что она не зависит от концентрации реагентов и продуктов. Это значит, что увеличение концентрации одного из веществ приводит к такому изменению концентрации других веществ, что константа равновесия остается неизменной. Если увеличить [A], то [B] уменьшится, а [C] и [D] увеличатся. В то же время константа равновесия зависит от температуры: с увеличением температуры она увеличивается для эндотермических и уменьшается для экзотермических реакций.

В выражение закона действующих масс включаются только концентрации растворов, концентрации или давления газов; конденсированные вещества в собственной фазе (Н₂О_(ж), КСl_(т) и т.п.) в формулу не включаются. Например, для реакции

Так как Fe₂O₃, Fe и H₂O- конденсированные вещества, то равновесие реакции зависит только от концентрации Н_2.

Константа равновесия — важнейшая термодинамическая характеристика реакции. По величине константы равновесия (К) можно судить о степени протекания реакции. При очень большом значении К равновесие реакции сильно сдвинуто вправо (в сторону продуктов), а при очень низком значении К реакция протекает в очень незначительной степени и равновесная смесь содержит преимущественно реагенты. Кроме того, по величине К можно вычислять концентрации реагентов и продуктов при достижении равновесия и, как будет показано ниже, DG реакции.

Видео:Влияние концентрации на скорость химических реакций. 10 класс.Скачать

Особенности кинетики гетерогенных реакций

Особенности кинетики гетерогенных реакций.

Химические реакции, протекающие на границе раздела фаз, называют гетерогенными. Гетерогенные процессы широко распространены в природе и часто используются на практике. Примерами могут служить процессы растворения, кристаллизации, испарения, горение твердого топлива, окисления металлов, реакции, идущие на поверхности твердых катализаторов.

Примерами некоторых типов гетерогенных реакций служат:

1) реакции окисления металлов (Т₁ + Г = Т₂)

2) реакция разложения карбоната кальция (T₁= T₂ + Г)

3) реакции с участием трех твердых фаз ( Т₁ + Т₂ = Т₃)

В гетерогенных реакциях можно выделить по меньшей мере три стадии: 1 – перенос реагирующих веществ к поверхности раздела фаз, т.е. в реакционную зону;

2 – собственно химическое взаимодействие;

3 – перенос продуктов реакции из реакционной зоны.

М.б. и другие стадии, например, адсорбция и десорбция; комплексооборазование и т.д.

Скорость процесса определяется лимитирующей (наиболее медленной) стадией. Если скорость собственно химического взаимодействия значительно больше скорости подвода реагентов к реакционной зоне и отвода продуктов от нее, то общая скорость процесса будет соответствовать скорости переноса реагентов и продуктов, она будет определяться процессами диффузии веществ.

Диффузия – это направленное перемещение вещества из области с большей концентрацией в область с меньшей концентрацией.

Предположим, что при низкой температуре лимитирующей стадией гетерогенного процесса является химическая реакция (кинетическая область). При повышении температуры константа скорости химической реакции быстро увеличивается, и начиная с некоторой температуры, когда скорость реакции станет больше скорости диффузии, лимитирующей стадией становится процесс диффузии (диффузионная область). Происходит переход из кинетической области гетерогенного процесса в диффузионную.

Зависимость логарифма скорости от температуры:

В промежуточной области ВС гетерогенная реакция контролируется как диффузией, так и химической реакцией на границе раздела фаз.

Скорость гетерогенной химической реакции измеряется изменением поверхностной концентрации одного из веществ (газа или жидкости), участвующих в реакции, за единицу времени

Концентрации веществ в твердом состоянии постоянны, поэтому в кинетическое уравнение реакций они не входят. Например, в реакции

CaCO3(т) = CaO(т) + CO2(г)

соударения меду молекулами СО2 могут происходить только на поверхности раздела фаз. В этом случае в выражение скорости реакции, согласно основному закону химической кинетики, в выражение скорости реакции будет входить только поверхностная концентрация СО2:

По этой ссылке вы найдёте полный курс лекций по математике:

ВОПРОС 7. Гетерогенные равновесия. Правило фаз.

При изучении различных систем важную роль играет понятие фазы. Как мы уже с вами говорили, фаза – это совокупность всех однородных частей системы, обладающих одинаковыми химическими свойствами и отделенная от остальных частей системы поверхностью.

На границе между двумя фазами всегда существует некоторая поверхность раздела, при переходе через которую многие свойства системы испытывают резкие скачкообразные изменения

Гетерогенные равновесия в процессах перехода вещества из одной фазы в другую, не сопровождающиеся изменением химического состава этого вещества, называются фазовыми равновесиями.

К таким равновесиям можно отнести состояния системы:

испарение конденсация; плавление кристаллизация;

сублимация кристаллизация и др.

Общим законом гетерогенных равновесий является правило фаз: в равновесной системе число фаз Ф, число степеней свободы С и число концентраций независимых компонентов К связаны простым соотношением С + Ф = К + n или С = К + n – Ф,

где n – число условий (температура среды, внешнее давление, магнитное поле, гравитационное поле и т.д.), которые могут влиять на равновесие в гетерогенной системе.

При исследовании гетерогенных равновесий в основном используют влияние на системы температуры среды и внешнего давления, тогда соотношение преобразуется в уравнение:

Для конденсированных систем, в которых практически отсутствует газовая фаза (например, в системе металл расплав, давление паров металла очень мало, им можно пренебречь и внешнее давление будет величиной постоянной), соотношение примет вид:

Компонентом называется химически однородная составная часть, которая после выделения из системы, может существовать в изолированном состоянии продолжительное время.

В трехфазной системе лед пар всего один компонент – Н2О.

В насыщенном водном растворе хлорида натрия (трехфазная система – кристаллический NaCl, насыщенный раствор NaCl, водяной пар) – два компонента: Н2О и NaCl. Ионы Na+ и Cl- компонентами не являются, т.к. не могут существовать в изолированном состоянии после их выделения из системы.

Возможно вам будут полезны данные страницы:

Компоненты подразделяются на независимые и зависимые. Концентрацию независимых компонентов можно задавать произвольно, концентрации зависимых компонентов определяются уравнениями реакций, протекающих в системе.

В системах, составные части которых реагируют друг с другом (химические системы), число независимых компонентов равно числу составных частей минус число обратимых реакций, протекающих в данной системе.

Система CaCO3 CaO + CO2 состоит из трех фаз (две твердые и одна газообразная), содержит три составные части и одну обратимую реакцию, число независимых компонентов будет:

3 (составные части) – 1 (обратимая реакция) = 2.

Следовательно, числа молей двух веществ можно изменять произвольно, концентрация третьего вещества — величина зависимая и определяется из уравнения реакции.

В физических системах, составные части которых не реагируют друг с другом, число независимых компонентов К равно числу составных частей системы. Например, в воздухе (смеси N2, O2, H2 и других газов) число независимых компонентов равно числу составляющих его газов.

Системы с одним независимым компонентом (К=1) называются однокомпонентными, с двумя независимыми компонентами (К=2) – двухкомпонентными и т.д.

Количество концентраций независимых

компонентов и условий, влияющих на равновесие в системе, которые можно произвольно увеличивать или уменьшать без изменения числа и вида фаз (без нарушения гетерогенного равновесия), составляет число степеней свободы С данной системы и рассчитывается по уравнению фаз.

Число степеней свободы определяет вариантность системы.

Системы без степеней свободы (С=0) называются безвариантными (инвариантными), системы с одной степенью свободы (С=1) – одновариантными (моновариантными), системы с двумя степенями свободы (с=2) – двухвариантными или бивариантными и т.д.

Например, охарактеризовать систему: FeO(k) + C(кокс) = Fe(k)+CO(г)

и определить ее вариантность.

1. Система химическая, равновесная.

2. Система гетерогенная

3. Число составных частей (компонентов) равно 4: FeO, C, Fe, CO. Каждое вещество можно выделить из системы и в изолированном виде оно может существовать сколько угодно долго.

4. Систему составляют 4 фазы: три твердых и одна газовая (Ф=4).

5. Число независимых компонентов равно 3 (4 составные части – 1 химическая реакция).

6. По уравнению определяем число степеней свободы:

С = К + 2 – ф = 3 + 2 – 4 = 1, т.е. система одновариантна. Следовательно, из всех условий, которые влияют на равновесие в системе, произвольно изменять можно только одно (температуру или давление).

Схематическая Р-t диаграмма воды, показывающая условия существования различных фаз.

При изучении фазовых равновесий широко применяется графический метод, при этом на основании опытных данных строят диаграммы состояния. Диаграмма состояния м.б. построена для любого вещества. Она позволяет определить условия, при которых будут устойчивы данная фаза или равновесие фаз. Рассмотрим диаграмму состояния воды, отвечающую трехфазной системе лед пар, в которой один компонент – вода (к=1). ханизм действия.

Электрохимическая защита эффективна в коррозионных средах с хорошей электрической проводимостью и основана на снижении скорости коррозии торможением анодных или катодных реакций путем поляризации (изменения потенциала) защищаемой конструкции (катода или анода) постоянным током.

В зависимости от вида поляризации различают катодную и анодную защиты.

Катодную поляризацию, а следовательно, и катодную защиту осуществляют двумя способами:

1) подключением защищаемой конструкции к отрицательному полюсу внешнего источника постоянного тока. Соответствующую разновидность катодной защиты называют защитой внешним (наложенным) потенциалом (рис.1).

2) Присоединением к защищаемой конструкции электрода («жертвенного» анода, или протектора), изготовленного из металла, имеющего меньший электродный потенциал, чем потенциал защищаемой конструкции. Разновидность катодной защиты в этом случае называют протекторной (гальванической) защитой, или защитой «жертвенным» анодом (рис.2).

Анодную защиту осуществляют присоединением защищаемой конструкции к положительному полюсу внешнего источника постоянного тока, а вспомогательного электрода — к отрицательному, при этом конструкция — анод, а электрод — катод. Анодная защита в отличие от катодной применима только к легкопассивируемым металлам.

Каждой фазе (трехфазной системы) отвечает определенное поле диаграммы, отделенное от полей других фаз линией.

На поле каждой фазы выберем по точке (1,2,3), которые характеризуют состояние фаз в данных условиях, и рассчитаем для этих состояний числа степеней свободы: С = К + 2 – Ф = 1 + 2 – 1 = 2. Это значит, что в каждом из этих состояний системы дивариантны. Он имеют две степени свободы: можно произвольно и независимо друг от друга изменять до определенного предела без нарушения фазового равновесия (без изменения числа и вида фаз) два условия. Например, для воды в состоянии 2 можно произвольно увеличивать или уменьшать Р и t до граничных линий, по достижении которых состояние фаз (фазового равновесия) нарушается (появляются новые фазы – лед и пар).

Граничные линии между полями на диаграмме характеризуют равновесие между двумя соседними фазами. Кривая ОА отвечает равновесию в системе вода пар, кривая ОВ – равновесию в системе лед вода, то есть каждая кривая соответствует двухфазной системе. Для каждого равновесия выберем по состоянию на диаграмме, обозначим эти состояния точками (I, II, III) и рассчитаем для каждого из них число степеней свободы: С = 1 + 2 – 2 = 1. Это значит, что все три системы в выбранных состояниях моновариантны (имеют по одной степени свободы), для них можно произвольно изменять только одно условие: температуру или давление. Например, для состояния II будем повышать температуру, оставив неизменным давление, то сразу же исчезнет жидкая фаза (фазовое равновесие нарушится). Чтобы это равновесие не нарушалось, вместе с ростом температуры должно повышаться давление и положение равновесия на диаграмме (точка II) сместится вверх по кривой ОС. В этом случае температура будет степенью свободы, а давление окажется зависимым от нее условием, т.е. не будет степенью свободы. Если произвольно менять давление, то температура станет зависимым условием.

В точке О пересекаются все три кривые. Эта точка отвечает равновесию между тремя фазами системы лед пар и называется тройной

точкой. Число степеней свободы системы в этом состоянии будет

С = 1 + 2 –3 = 0, т.е. система безвариантна, ни одно из ее условий менять нельзя. Стоит произвольно изменить хотя бы одно из условий — сразу же нарушится вазовое равновесие (исчезнут сразу две фазы). При одновременном изменении температуры и давления исчезнет одна фаза. Равновесие в этой системе возможно при определенных условиях:

Р= 610,5 Па, t = 0, 0099 0С.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Скорость химических реакций. 9 класс.Скачать

Кинетические уравнения скоростей гетерогенной реакции

§9.5 Реакции гомогенные и гетерогенные. Факторы, влияющие на скорость химической реакции.

Кинетические уравнения, рассмотренные в предыдущем параграфе, справедливы только для гомогенных реакций, т.е. для таких реакций, которые идут в какой-нибудь одной фазе – газовой или жидкой. Например, это могут быть реакции между двумя газами, либо реакции, протекающие при сливании растворов:

NaOH(р-р) + HCl(р-р) = NaCl(р-р) + H₂O.

Но существует и множество других реакций, происходящих на границах раздела фаз – между газообразным веществом и раствором, между раствором и твердым веществом, между твердым и газообразным веществами. Такие реакции называются гетерогенными. В качестве типичного примера гетерогенной реакции рассмотрим лабораторный метод получения водорода из металлического цинка и разбавленной серной кислоты:

Рис. 9-11. Разная скорость реакции в опытах с одной крупной или несколькими мелкими гранулами цинка в серной кислоте.

Цинк в виде гранул (кусочки металла неправильной формы и разной величины) помещают в разбавленный раствор серной кислоты и собирают выделяющийся газообразный водород. В пробирке с одной крупной гранулой реакция идет заметно медленнее (рис. 9-11). При одинаковой массе цинка в пробирках количество выделившегося водорода в обоих опытах будет одинаковым, но в пробирке с мелкими гранулами реакция закончится быстрее. Причина в том, что реакция между цинком и раствором серной кислоты идет только на поверхности контакта гранул с раствором (граница раздела фаз), а общая поверхность у нескольких мелких гранул больше, чем у одной крупной гранулы той же массы. Цинк в виде порошка для этой реакции использовать просто опасно – реакция начинает идти настолько быстро, что смесь выплескивается из пробирки.

Для такой гетерогенной реакции уже нельзя записать кинетическое уравнение вида:

** Но и такое уравнение не сможет достаточно хорошо описывать скорость нашей реакции. Во-первых, в ходе реакции гранулы постепенно уменьшаются в размерах, площадь их поверхности меняется и константа скорости реакции k уже не может учитывать это изменение. Если использовать гранулы из очень чистого цинка, то к ним «прилипает» образующийся водород (как это ни удивительно) и площадь контакта реагентов меняется непредсказуемо. Во-вторых, на поверхности раздела фаз концентрация серной кислоты совсем не такая, как в верхних слоях раствора. В зоне реакции активно образуется раствор соли ZnSO₄, который вытесняет раствор серной кислоты с поверхности гранул.

Итак, мы видим, что в общем случае скорость гетерогенной реакции зависит от:
а) скорости подвода реагентов к границе раздела фаз;
б) скорости реакции на поверхности раздела фаз, которая зависит от площади этой поверхности;
в) скорости отвода продуктов реакции от границы раздела фаз.

Стадии (а) и (в) называются диффузионными, (см. словарь терминов) а стадия (б) – кинетической. Та стадия, которая протекает наиболее медленно, называется лимитирующей – именно она определяет скорость реакции в целом.

Универсального выражения для скорости гетерогенных реакций не существует, поскольку каждая из стадий (а-в) при определенных условиях может быть лимитирующей. Но в некоторых случаях, когда диффузионные стадии заведомо не являются лимитирующими из-за активного перемешивания реагентов, а площадь поверхности раздела фаз меняется медленно, можно экспериментально получить кинетические уравнения типа (2), удовлетворительно описывающие протекание гетерогенных реакций. Это имеет важное значение для химического производства, где большинство используемых реакций – гетерогенные.

Когда на экзамене абитуриента просят перечислить факторы, влияющие на скорость химической реакции, то обычно ожидают такого ответа:
— природа реагирующих веществ,
— концентрация реагентов,
— температура,
— наличие катализатора.

** На самом деле этот перечень шире: мы уже знаем, что на скорость гетерогенных реакций сильное влияние оказывает площадь поверхности раздела фаз и диффузия. Однако полезно обобщить перечисленные выше четыре фактора, понимая при этом, что они имеют отношение главным образом к гомогенным реакциям.

Под влиянием природы реагирующих веществ обычно подразумевают то простое обстоятельство, что разные вещества реагируют по-разному. Это тривиальное наблюдение можно сделать более ценным, если анализировать примеры разной реакционной способности сходных по строению веществ в однотипных реакциях. Например, реакция газообразного иодистого водорода с кислородом при комнатной температуре идет с заметной скоростью:

Аналогичная реакция газообразных HCl и O₂ с образованием хлора и воды при комнатной температуре идет очень медленно. Обе реакции – окислительно-восстановительные и для их протекания атом галогена в молекулах HCl или HI должен передать электрон кислороду (убедитесь в этом, расставив степени окисления над атомами в уравнении реакции). Иод в молекуле HI – более подходящий донор электрона, т.к. его валентная оболочка находится существенно дальше от ядра, чем у атома хлора в молекуле HCl. Таким образом, знание электронного строения атомов и молекул реагирующих веществ часто позволяет качественно оценить относительные скорости некоторых реакций. Также под природой реагирующих веществ иногда могут подразумевать степень их раздробленности в гетерогенных реакциях.

Влияние концентрации реагентов на скорость реакций мы уже достаточно подробно обсудили – кинетические уравнения количественно учитывают этот фактор.

Что касается влияния температуры, то этот фактор действует одинаково как на скорость реакции v, так и на константу скорости k – обе эти величины быстро возрастают с повышением температуры. Полезно рассмотреть влияние температуры именно на константу скорости – в этом случае нашу задачу не осложняют постоянно меняющиеся в ходе реакции концентрации реагирующих веществ.

Еще в XIX веке голландский физикохимик Вант-Гофф опытным путем обнаружил, что при повышении температуры на 10 о С скорости многих реакций возрастают в 2-4 раза. На языке химической кинетики правило Вант-Гоффа можно выразить следующим соотношением:

Здесь γ (греческая буква «гамма») — так называемый температурный коэффициент или коэффициент Вант-Гоффа, k_t и k_t+10 – константы скорости реакции при температурах t и (t + 10) о С. Для каждой конкретной реакции температурный коэффициент определяется опытным путем. Он показывает, во сколько именно раз возрастает скорость данной химической реакции (и ее константа скорости) при повышении температуры на каждые 10 градусов.

Температурные коэффициенты используют главным образом в учебной литературе – для нужд химической кинетики они мало пригодны, поскольку не сохраняют строго постоянных значений в разных интервалах температур. Но нам с вами температурные коэффициенты позволят наглядно разобраться в характере зависимости скорости реакции от температуры. Эта зависимость нелинейная, т.е. скорость реакции возрастает гораздо быстрее, чем температура.

Покажем это на примере реакции, с температурным коэффициентом γ = 2,9. Допустим, мы хотим выяснить, во сколько раз возрастет скорость реакции (и константа скорости k) при повышении температуры от 50 о С до 100 о С. Примем за единицу константу скорости при 50 о С (k₅₀ = 1). Через 10 о (т.е. при 60 о С) константа k вырастет в 2,9 раза: k₆₀ = 2,9. Еще через 10 о (при 70 о С) значение константы составит: k₇₀ = k₆₀ . 2,9 = 2,9 2 . Так, продолжая добавлять 10-градусные интервалы, мы придем к значению k₁₀₀ = 2,9 5 . В общем случае:

Где n – число 10-градусных интервалов в заданном интервале повышения температуры. В нашем примере при повышении температуры от 50 о до 100 о таких интервалов 5. При этом мгновенная скорость реакции и константа скорости реакции возрастут примерно в 595 раз:

** Правило Вант-Гоффа используется для приближенной оценки изменения константы скорости реакции при повышении или понижении температуры. Более точное соотношение между константой скорости и температурой установил шведский химик Сванте Аррениус:

Здесь k – константа скорости, e – важное в математике число (равное приблизительно 2,71 и возникающее во многих математических преобразованиях), R – газовая постоянная, T – абсолютная температура в Кельвинах (об R и T см. в §5.6 книги 1), E_a – энергия активации. Еще одна постоянная А – «константа Аррениуса» или «предэкспонента» определяется для каждой конкретной реакции и имеет ту же размерность, что и константа скорости k.

Многие наши читатели пока не знакомы с логарифмами, поэтому здесь мы не будем приводить способ решения такого уравнения. Для нас сейчас важен общий нелинейный характер зависимости константы скорости k от температуры, а также характер связи между скоростью реакции и энергией активации. Если левую и правую части уравнения Аррениуса разделить на постоянную А и записать число e его приближенным численным значением, то уравнение примет вид:

Напомним, что E_a – величина примерно постоянная для каждой реакции, не зависящая от температуры. В полученном выражении она входит в показатель степени при 2,71. Чем больше E_a конкретной реакции, тем больше будет знаменатель дроби и тем меньше (при данной температуре) будет константа скорости k (и скорость) этой реакции. Если же рассматривать какую-нибудь одну реакцию (с фиксированной E_a) при разных температурах, то повышение Т быстро уменьшает нижнюю часть дроби и, следовательно, измеряемая k будет быстро расти.

Повышение температуры приводит к быстрому увеличению числа «энергичных» молекул, способных преодолевать активационный барьер E_a. При прочих равных условиях чем выше барьер E_a, тем меньше скорость реакций. Многие (даже энергетически выгодные, экзотермические реакции) могут идти с заметной скоростью лишь в очень жестких условиях именно из-за высокой энергии активации. К таким реакциям, например, относится получение аммиака NH₃ из азота и водорода. Аммиак является важнейшим сырьем для производства многих химических продуктов. Задачу его синтеза (как и синтеза множества других полезных соединений) позволяет решить применение катализаторов — веществ, способных понижать энергию активации реакции E_a. Катализаторы не расходуются в ходе реакции, поэтому достаточно сравнительно небольшого их количества для переработки большой массы реагентов. Значительное повышение скорости реакций под влиянием таких веществ называется катализом. Этому химическому феномену посвящен следующий параграф нашего учебника.

9.18 . Во сколько раз увеличится константа скорости химической реакции при повышении температуры на 30 о С, если γ = 4?

9.19 . На сколько градусов следует повысить температуру, чтобы константа скорости реакции выросла в 32 раза (γ = 2)?

9.20 . При повышении температуры с 20 о С до 60 о С скорость реакции возрастает в 150 раз. Вычислите температурный коэффициент реакции.

9.21 (ФМШ). Температурный коэффициент газовой реакции 2А + В = С равен 3. Как изменится константа скорости реакции при повышении температуры от 20 о С до 80 о С и одновременном увеличении давления в 2 раза?