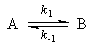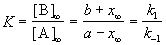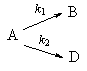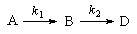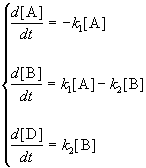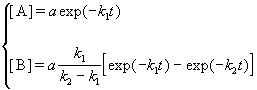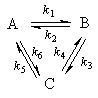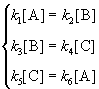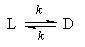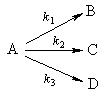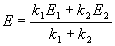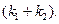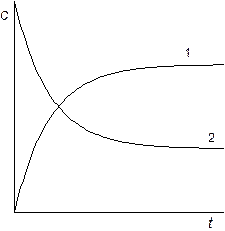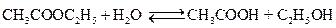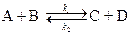Кинетические уравнения для обратимых реакций

Видео:Составляем кинетические уравненияСкачать

Кинетические уравнения для обратимых реакций

При изучении кинетики сложных реакций, включающих несколько элементарных стадий, используют принцип независимости химических реакций:

Если в системе протекает несколько простых реакций, то каждая из них подчиняется основному постулату химической кинетики независимо от других реакций.

Основные типы сложных реакций мы рассмотрим на примере реакций первого порядка.

1. Обратимые реакции первого порядка:

Закон действующих масс записывается следующим образом:

.

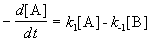
Если начальные концентрации веществ A и B обозначить, соответственно, a и b и ввести степень превращения x ([A] = a — x, [B] = b + x), то кинетическое уравнение приобретает вид:

.

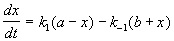
Решение этого уравнения можно выразить через степень превращения, соответствующую достижению равновесия:

или , (5.1)

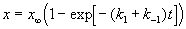
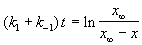
где x определяется условием равенства скоростей прямой и обратной реакций:

, откуда следует: . (5.2)

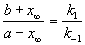
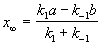
При t наступает равновесие, которое характеризуется константой:

2. Параллельные реакции первого порядка:

Кинетическое уравнение записывается с учетом принципа независимости:

.

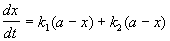
Решение этого уравнения записывается так же, как и для одной реакции первого порядка:

, . (5.3)

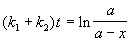
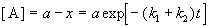
Для параллельных реакций в любой момент времени отношение концентраций продуктов постоянно и определяется константами скорости элементарных стадий:

.

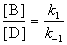
3. Последовательные реакции первого порядка:

Пусть в начальный момент времени есть только вещество A. Применим к этой системе закон действующих масс и принцип независимости химических реакций:

Решение этой системы дает концентрации веществ:

Концентрация промежуточного вещества достигает максимума при

.

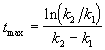
Величина этого максимума определяется отношением констант k₂ / k₁. Если оно велико, т.е. k₂ >> k₁, то промежуточный продукт не успевает накапливаться и его концентрация в любой момент времени мала. В этом случае для анализа кинетических уравнений можно использовать приближенный метод квазистационарных концентраций ( 6).

Пример 5-1. Для обратимой реакции первого порядка

K_равн = 8, а k₁ = 0.4 с -1 . Вычислите время, при котором концентрации веществ A и B станут равными, если начальная концентрация вещества B равна 0.

Решение. Из константы равновесия находим константу скорости обратной реакции:

с -1 .

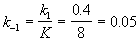
По условию, мы должны найти время, за которое прореагирует ровно половина вещества A. Для этого надо подставить значение x(t) = a/2 в решение кинетического уравнения для обратимых реакций (5.1) и (5.2):

c.

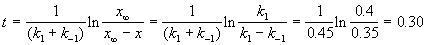
Пример 5-2. В параллельных реакциях первого порядка

выход вещества B равен 63%, а время превращения A на 1/3 равно 7 минутам. Найдите k₁ и k₂.

Решение. Кинетическое уравнение (5.3) для разложения вещества в параллельных реакциях имеет вид уравнения первого порядка, в которое вместо одной константы скорости входит сумма констант скорости отдельных стадий. Следовательно, по аналогии с реакциями первого порядка, по времени превращения A на 1/3 (x(t) = a/3) можно определить сумму констант k₁ + k₂:

мин -1 .

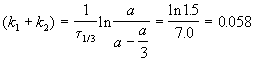
Выход вещества В равен 63%, а вещества D — 37%. Отношение этих выходов равно отношению конечных концентраций веществ B и D, следовательно оно равно отношению соответствующих констант скорости:

.

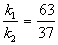
Решая это уравнение совместно с предыдущим, находим: k₁ = 0.037 мин -1 , k₂ = 0.021 мин -1 .

Пример 5-3. Имеется следующее равновесие:

Как связаны между собой константы k₁ — k₆?

Решение основано на принципе детального равновесия:

Если сложная система находится в равновесии, то в каждой из элементарных стадий также соблюдается равновесие.

Это означает, что во всех трех процессах: A B, B C и C A скорости прямой и обратной реакций равны:

Перемножив почленно эти три равенства и поделив левую и правую части на произведение равновесных концентраций [A] . [B]. [C], находим искомое соотношение между константами скорости:

.

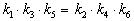
5-1. Нарисуйте графики зависимости концентраций веществ A и B от времени в обратимой реакции A B для двух случаев: 1) k₁ > k_-1; 2) k₁ -1 . Вычислите время, при котором концентрации веществ A и B станут равными, если начальная концентрация вещества B равна 0.(ответ)

5-5. Превращение роданида аммония NH₄SCN в тиомочевину (NH₄)₂CS — обратимая реакция первого порядка. Рассчитайте константы скорости прямой и обратной реакций, используя следующие экспериментальные данные:

t, мин

Доля прореагировавшего NH₄SCN, %

5-6. Один из методов оценки возраста биологических объектов основан на измерении содержания в них оптических изомеров аминокислот. В живых организмах отношение концентраций D- и L-изомеров постоянно ([D]₀ / [L]₀ = a). В мертвых организмах происходит рацемизация:

Чему равен возраст биологического объекта, в котором [D] / [L] = b? Решите задачу в общем виде и для образца, содержащего аспарагиновую кислоту (k = 1.48 . 10 -5 лет -1 , a = 0.07, b = 0.27).(ответ)

5-7. В параллельных реакциях первого порядка

выход вещества B равен 53%, а время превращения A на 1/3 равно 40 c. Найдите k₁ и k₂.(ответ)

5-8. Реакция разложения вещества А может протекать параллельно по трем направлениям:

Концентрации продуктов в смеси через 5 мин после начала реакции были равны: [B] = 3.2 моль/л, [C] = 1.8 моль/л, [D] = 4.0 моль/л. Определите константы скорости k₁ — k₃, если период полураспада вещества А равен 10 мин.(ответ)

5-9. Реакция разложения вещества А может протекать параллельно по трем направлениям:

Концентрации продуктов в смеси через 10 мин после начала реакции были равны: [B] = 1.6 моль/л, [C] = 3.6 моль/л, [D] = 7.8 моль/л. Определите константы скорости k₁ — k₃, если период полураспада вещества А равен 8 мин.(ответ)

5-10. Покажите, что при двух параллельных реакциях

энергия активации суммарной реакции разложения A связана с энергиями активации отдельных стадий следующим образом:

*5-11. В системе идут две параллельные газофазные реакции: А + B C (k₁), A D (k₂). Исходная смесь эквимолекулярна, начальное давление составляет 200 мм рт. ст. При практически полном превращении А при 227 о С Р_С = 10 мм рт.ст., а при 327 о С Р_С = 39 мм рт.ст. Найдите разность энергий активации этих реакций.(ответ)

5-12. На одном графике нарисуйте зависимости концентрации вещества B от времени в системе последовательных реакций A B D для двух случаев: 1) k₁ >> k₂; 2) k₁ > 1; 2) k₂ / k₁

Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору

Видео:Влияние концентрации на скорость химических реакций. 10 класс.Скачать

Кинетика двусторонних (обратимых) химических реакций

1. Рассмотрим двустороннюю (обратимую) реакцию

,

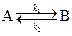
протекающую в закрытой системе при постоянном объеме, когда обе стадии, прямая и обратная, являются реакциями первого порядка. Если скорости прямой и обратной реакций в изучаемом диапазоне условий соизмеримы, то, согласно закону действующих масс, выражение для суммарной скорости записывается в виде разности скоростей прямой и обратной реакций.

(4.69)

. (4.70)

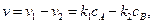
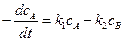
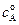
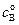
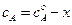
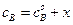
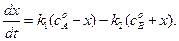
Пусть начальные концентрации веществ А и В равны соответственно и , а количество прореагировавшего вещества А в единице объема, то есть уменьшение концентрации вещества А к моменту времени t равно х. Из условия материального баланса можно записать и . После введения этих обозначений, уравнение (4.70) можно записать в следующем виде:

(4.71)

Преобразуя уравнение (4.71), получим:

. (4.72)

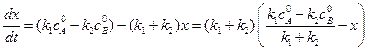
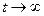
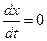
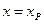
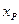
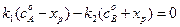
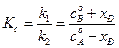
В момент равновесия ( ) скорость двусторонней реакции будет равна нулю, то есть и , где — количество вещества А в единице объема, прореагировавшего к моменту установления равновесия. Тогда , откуда

, (4.73)

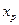
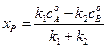
где K_с –константа равновесия реакции. Решив уравнение (4.73) относительно получим соотношение:

. (4.74)

Подставив (4.74) в (4.72) получим:

(4.75)

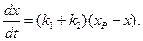
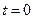
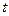
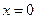
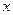
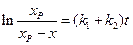
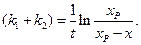
Разделяя переменные и интегрируя от до и от до получим:

и (4.76)

(4.77)

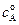
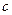
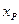
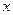
Уравнение (4.77) аналогично уравнению (4.24) для односторонней реакции первого порядка, с той лишь разницей, что вместо и , в нем фигурируют соответственно и , а в качестве кинетического параметра – сумма констант скоростей

Количество вещества, вступившего в реакцию к моменту времени t можно рассчитать, по соотношению:

. (4.78)

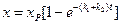
Изменение концентрации реагентов и продуктов реакции во времени можно изобразить на графике (рис 6).

Рис. 6 Зависимость концентрации реагентов от времени

Для обратимой реакции первого порядка.1 – продукт реакции, 2 –исходное вещество.

Выражение (4.78)можно также представить в виде уравнения прямой линии:

(4.78)

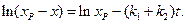
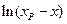
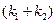
Таким образом, для обратимой реакции первого порядка должна соблюдаться линейная зависимость функции от времени. Из значения тангенса угла наклона прямой можно вычислить сумму констант скоростей прямой и обратной реакций – .

Для расчета значений каждой из констант, необходимо рассчитать константу равновесия реакции 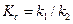из термодинамических (можно справочных) данных или по формуле (4.73):

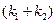
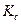
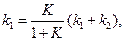
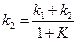
Зная значения и , нетрудно рассчитать каждую из констант отдельно:

. (4.79)

2. Типичным примером обратимой химической реакции, в которой обе реакции протекают как реакции второго порядка, является реакция омыления сложного эфира

Схема такой реакции

Решение задачи рассмотрим для случая, когда продукты реакции до начала реакции в реакционной смеси отсутствуют: С_А 0 = С_В 0 =а.

Уравнение скорости химической реакции можно записать в виде:

. (4.80)

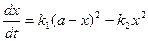
При достижении состояния равновесия выполняется условие:

. (4.81)

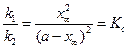
С учетом уравнения (4.81) уравнение (4.80) для скорости химической реакции запишется как:

. (4.82)

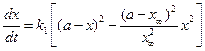
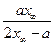
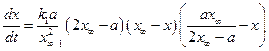
Полином допускает наличие двух корней квадратного уравнения х₁= х_∞ и х₂= , его записывают через произведение вида: m(х—х₁) (х—х₂). Уравнение скорости химической реакции запишется как:

. (4.83)

Интегральная форма этого уравнения имеет вид

. (4.84)

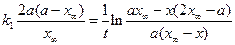
Константы скоростей k₁ и k₂можно определить из опытного значения кажущейся константы скорости:

и . (4.85)

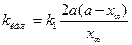
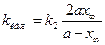
Дата добавления: 2016-01-09 ; просмотров: 2172 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Химическая кинетика. Формальная кинетика простых гомогенных реакций в закрытых системахСкачать

Кинетика двусторонних (обратимых) реакций

Химические реакции часто являются двусторонними (обратимыми), т.е. могут протекать при данных условиях в двух противоположных направлениях (понятие обратимая реакция следует отличать от термодинамического понятия обратимый процесс; двусторонняя реакция обратима в термодинамическом смысле лишь в состоянии химического равновесия). Рассмотрим элементарную двустороннюю реакцию

Скорость уменьшения концентрации вещества А при протекании прямой реакции определяется уравнением (II.40):

, (II.40)

а скорость возрастания концентрации вещества А в результате протекания обратной реакции – уравнением (II.41):

(II.41)

Общая скорость двусторонней реакции в любой момент времени равна разности скоростей прямой и обратной реакции:

(II.42)

По мере протекания двусторонней реакции скорость прямой реакции уменьшается, скорость обратной реакции – увеличивается; в некоторый момент времени скорости прямой и обратной реакции становятся равными и концентрации реагентов перестают изменяться. Таким образом, в результате протекания в закрытой системе двусторонней реакции система достигает состояния химического равновесия; при этом константа равновесия будет равна отношению констант скоростей прямой и обратной реакции:

(II.43)

Кинетика гетерогенных химических реакций

Когда реакция совершается между веществами, находящимися в разных фазах гетерогенной системы, основной постулат химической кинетики становится неприменимым. В гетерогенных реакциях роль промежуточных продуктов обычно играют молекулы, связанные химическими силами с поверхностью раздела фаз (химически адсорбированные на поверхности). Во всяком гетерогенном химическом процессе можно выделить следующие стадии:

1. Диффузия реагентов к реакционной зоне, находящейся на поверхности раздела фаз.

2. Активированная адсорбция частиц реагентов на поверхности.

3. Химическое превращение адсорбированных частиц.

4. Десорбция образовавшихся продуктов реакции.

5. Диффузия продуктов реакции из реакционной зоны.

Стадии 1 и 5 называются диффузионными, стадии 2, 3 и 4 – кинетическими. Универсального выражения для скорости гетерогенных химических реакций не существует, поскольку каждая из выделенных стадий может являться лимитирующей. Как правило, при низких температурах скорость гетерогенной реакции определяют кинетические стадии (т.н. кинетическая область гетерогенного процесса; скорость реакции в этом случае сильно зависит от температуры и величины площади поверхности раздела фаз; порядок реакции при этом может быть любым). При высоких температурах скорость процесса будет определяться скоростью диффузии (диффузионная область гетерогенной реакции, характеризующаяся, как правило, первым порядком реакции и слабой зависимостью скорости процесса от температуры и площади поверхности раздела фаз).

ФОТОХИМИЧЕСКИЕ РЕАКЦИИ

Передача энергии для активации вступающих во взаимодействие молекул может осуществляться либо в форме теплоты (т. н. темновые реакции), либо в виде квантов электромагнитного излучения. Реакции, в которых активация частиц является результатом их взаимодействия с квантами электромагнитного излучения видимой области спектра, называют фотохимическими реакциями. При всех фотохимических процессах выполняется закон Гротгуса:

Химическое превращение вещества может вызвать только то излучение, которое поглощается этим веществом.

Взаимодействие света с веществом может идти по трем возможным направлениям:

1. Возбуждение частиц (переход электронов на вышележащие орбитали):

2. Ионизация частиц за счет отрыва электронов:

3. Диссоциация молекул с образованием свободных радикалов (гомолитическая) либо ионов (гетеролитическая):

Между количеством лучистой энергии, поглощенной молекулами вещества, и количеством фотохимически прореагировавших молекул существует соотношение, выражаемое законом фотохимической эквивалентности Штарка-Эйнштейна:

Число молекул, подвергшихся первичному фотохимическому превращению, равно числу поглощенных веществом квантов электромагнитного излучения.

Поскольку фотохимическая реакция, как правило, включает в себя и т.н. вторичные процессы (например, в случае цепного механизма), для описания реакции вводится понятие квантовый выход фотохимической реакции:

Квантовый выход фотохимической реакции γ есть отношение числа частиц, претерпевших превращение, к числу поглощенных веществом квантов света.

Квантовый выход реакции может варьироваться в очень широких пределах: от 10 -3 (фотохимическое разложение метилбромида) до 10 6 (цепная реакция водорода с хлором); в общем случае, чем более долгоживущей является активная частица, тем с большим квантовым выходом протекает фотохимическая реакция.

Важнейшими фотохимическими реакциями являются реакции фотосинтеза, протекающие в растениях с участием хлорофилла. Процесс фотосинтеза составляют две стадии: световая, связанная с поглощением фотонов, и значительно более медленная темновая, представляющая собой ряд химических превращений, осуществляемых в отсутствие света. Суммарный процесс фотосинтеза заключается в окислении воды до кислорода и восстановлении диоксида углерода до углеводов:

Протекание данного окислительно-восстановительного процесса (связанного с переносом электронов) возможно благодаря наличию в реакционном центре хлорофилла Сhl донора D и акцептора A электронов; перенос электронов происходит в результате фотовозбуждения молекулы хлорофилла:

DChlA + hν ––> DChl*A ––> DChl + A – ––> D + ChlA –

Возникающие в данном процессе заряженные частицы D + и A – принимают участие в дальнейших окислительно-восстановительных реакциях темновой стадии фотосинтеза.

КАТАЛИТИЧЕСКИЕ ПРОЦЕССЫ

Скорость химической реакции при данной температуре определяется скоростью образования активированного комплекса, которая, в свою очередь, зависит от величины энергии активации. Во многих химических реакциях в структуру активированного комплекса могут входить вещества, стехиометрически не являющиеся реагентами; очевидно, что в этом случае изменяется и величина энергии активации процесса. В случае наличия нескольких переходных состояний реакция будет идти в основном по пути с наименьшим активационным барьером.

Катализ – явление изменения скорости химической реакции в присутствии веществ, состояние и количество которых после реакции остаются неизменными.

Различают положительный и отрицательный катализ (соответственно увеличение и уменьшение скорости реакции), хотя часто под термином «катализ» подразумевают только положительный катализ; отрицательный катализ называют ингибированием.

Вещество, входящее в структуру активированного комплекса, но стехиометрически не являющееся реагентом, называется катализатором. Для всех катализаторов характерны такие общие свойства, как специфичность и селективность действия.

Специфичность катализатора заключается в его способности ускорять только одну реакцию или группу однотипных реакций и не влиять на скорость других реакций. Так, например, многие переходные металлы (платина, медь, никель, железо и т.д.) являются катализаторами для процессов гидрирования; оксид алюминия катализирует реакции гидратации и т.д.

Селективность катализатора – способность ускорять одну из возможных при данных условиях параллельных реакций. Благодаря этому можно, применяя различные катализаторы, из одних и тех же исходных веществ получать различные продукты:

Причиной увеличения скорости реакции при положительном катализе является уменьшение энергии активации при протекании реакции через активированный комплекс с участием катализатора (рис. 2.8).

Поскольку, согласно уравнению Аррениуса, константа скорости химической реакции находится в экспоненциальной зависимости от величины энергии активации, уменьшение последней вызывает значительное увеличение константы скорости. Действительно, если предположить, что предэкспоненциальные множители в уравнении Аррениуса (II.32) для каталитической и некаталитической реакций близки, то для отношения констант скорости можно записать:

(II.44)

Если ΔE_A = –50 кДж/моль, то отношение констант скоростей составит 27·10 5 раз (действительно, на практике такое уменьшение E_A увеличивает скорость реакции приблизительно в 10 5 раз).

Необходимо отметить, что наличие катализатора не влияет на величину изменения термодинамического потенциала в результате процесса и, следовательно, никакой катализатор не может сделать возможным самопроизвольное протекание термодинамически невозможного процесса (процесса, ΔG (ΔF) которого больше нуля). Катализатор не изменяет величину константы равновесия для обратимых реакций; влияние катализатора в этом случае заключается только в ускорении достижения равновесного состояния.

В зависимости от фазового состояния реагентов и катализатора различают гомогенный и гетерогенный катализ.

Рис. 2.8. Энергетическая диаграмма химической реакции без катализатора (1) и в присутствии катализатора (2).

Гомогенный катализ.

Гомогенный катализ – каталитические реакции, в которых реагенты и катализатор находятся в одной фазе. В случае гомогенно-каталитических процессов катализатор образует с реагентами промежуточные реакционноспособные продукты. Рассмотрим некоторую реакцию

В присутствии катализатора осуществляются две быстро протекающие стадии, в результате которых образуются частицы промежуточного соединения АК и затем (через активированный комплекс АВК # ) конечный продукт реакции с регенерацией катализатора:

Примером такого процесса может служить реакция разложения ацетальдегида, энергия активации которой E_A = 190 кДж/моль:

В присутствии паров йода этот процесс протекает в две стадии:

Уменьшение энергии активации этой реакции в присутствии катализатора составляет 54 кДж/моль; константа скорости реакции при этом увеличивается приблизительно в 10 5 раз. Наиболее распространенным типом гомогенного катализа является кислотный катализ, при котором в роли катализатора выступают ионы водорода Н + .

Автокатализ.

Автокатализ – процесс каталитического ускорения химической реакции одним из её продуктов. В качестве примера можно привести катализируемую ионами водорода реакцию гидролиза сложных эфиров. Образующаяся при гидролизе кислота диссоциирует с образованием протонов, которые ускоряют реакцию гидролиза. Особенность автокаталитической реакции состоит в том, что данная реакция протекает с постоянным возрастанием концентрации катализатора. Поэтому в начальный период реакции скорость её возрастает, а на последующих стадиях в результате убыли концентрации реагентов скорость начинает уменьшаться; кинетическая кривая продукта автокаталитической реакции имеет характерный S-образный вид (рис. 2.9).

Рис. 2.9. Кинетическая кривая продукта автокаталитической реакции

Гетерогенный катализ.

Гетерогенный катализ – каталитические реакции, идущие на поверхности раздела фаз, образуемых катализатором и реагирующими веществами. Механизм гетерогенно-каталитических процессов значительно более сложен, чем в случае гомогенного катализа. В каждой гетерогенно-каталитической реакции можно выделить как минимум шесть стадий:

1. Диффузия исходных веществ к поверхности катализатора.

2. Адсорбция исходных веществ на поверхности с образованием некоторого промежуточного соединения:

3. Активация адсорбированного состояния (необходимая для этого энергия есть истинная энергия активации процесса):

4. Распад активированного комплекса с образованием адсорбированных продуктов реакции:

5. Десорбция продуктов реакции с поверхности катализатора.

6. Диффузия продуктов реакции от поверхности катализатора.

Специфической особенностью гетерокаталитических процессов является способность катализатора к промотированию и отравлению.

Промотирование – увеличение активности катализатора в присутствии веществ, которые сами не являются катализаторами данного процесса (промоторов). Например, для катализируемой металлическим никелем реакции

введение в никелевый катализатор небольшой примеси церия приводит к резкому возрастанию активности катализатора.

Отравление – резкое снижение активности катализатора в присутствии некоторых веществ (т. н. каталитических ядов). Например, для реакции синтеза аммиака (катализатор – губчатое железо), присутствие в реакционной смеси соединений кислорода или серы вызывает резкое снижение активности железного катализатора; в то же время способность катализатора адсорбировать исходные вещества снижается очень незначительно.

Для объяснения этих особенностей гетерогенно-каталитических процессов Г.Тэйлором было высказано следующее предположение: каталитически активной является не вся поверхность катализатора, а лишь некоторые её участки – т.н. активные центры, которыми могут являться различные дефекты кристаллической структуры катализатора (например, выступы либо впадины на поверхности катализатора). В настоящее время нет единой теории гетерогенного катализа. Для металлических катализаторов была разработана теория мультиплетов. Основные положения мультиплетной теории состоят в следующем:

1. Активный центр катализатора представляет собой совокупность определенного числа адсорбционных центров, расположенных на поверхности катализатора в геометрическом соответствии со строением молекулы, претерпевающей превращение.

2. При адсорбции реагирующих молекул на активном центре образуется мультиплетный комплекс, в результате чего происходит перераспределение связей, приводящее к образованию продуктов реакции.

Теорию мультиплетов называют иногда теорией геометрического подобия активного центра и реагирующих молекул. Для различных реакций число адсорбционных центров (каждый из которых отождествляется с атомом металла) в активном центре различно – 2, 3, 4 и т.д. Подобные активные центры называются соответственно дублет, триплет, квадруплет и т.д. (в общем случае мультиплет, чему и обязана теория своим названием).

Например, согласно теории мультиплетов, дегидрирование предельных одноатомных спиртов происходит на дублете, а дегидрирование циклогексана – на секстете (рис. 2.10 – 2.11); теория мультиплетов позволила связать каталитическую активность металлов с величиной их атомного радиуса.

Рис. 2.10. Дегидрирование спиртов на дублете.

Рис. 2.11. Дегидрирование циклогексана на секстете.

Ферментативный катализ.

Ферментативный катализ – каталитические реакции, протекающие с участием ферментов – биологических катализаторов белковой природы. Ферментативный катализ имеет две характерные особенности:

1. Высокая активность, на несколько порядков превышающая активность неорганических катализаторов, что объясняется очень значительным снижением энергии активации процесса ферментами. Так, константа скорости реакции разложения перекиси водорода, катализируемой ионами Fе 2+ , составляет 56 с -1 ; константа скорости этой же реакции, катализируемой ферментом каталазой, равна 3.5·10 7 , т.е. реакция в присутствии фермента протекает в миллион раз быстрее (энергии активации процессов составляют соответственно 42 и 7.1 кДж/моль). Константы скорости гидролиза мочевины в присутствии кислоты и уреазы различаются на тринадцать порядков, составляя 7.4·10 -7 и 5·10 6 с -1 (величина энергии активации составляет соответственно 103 и 28 кДж/моль).

2. Высокая специфичность. Например, амилаза катализирует процесс расщепления крахмала, представляющего собой цепь одинаковых глюкозных звеньев, но не катализирует гидролиз сахарозы, молекула которой составлена из глюкозного и фруктозного фрагментов.

Согласно общепринятым представлениям о механизме ферментативного катализа, субстрат S и фермент F находятся в равновесии с очень быстро образующимся фермент-субстратным комплексом FS, который сравнительно медленно распадается на продукт реакции P с выделением свободного фермента; т.о., стадия распада фермент-субстратного комплекса на продукты реакции является скоростьопределяющей (лимитирующей).

F + S FS ––> F + P

Исследование зависимости скорости ферментативной реакции от концентрации субстрата при неизменной концентрации фермента показали, что с увеличением концентрации субстрата скорость реакции сначала увеличивается, а затем перестает изменяться (рис. 2.12) и зависимость скорости реакции от концентрации субстрата описывается следующим уравнением:

(II.45)

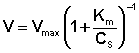
Здесь К_m – константа Михаэлиса, численно равная концентрации субстрата при V = ½V_max. Константа Михаэлиса служит мерой сродства между субстратом и ферментом: чем меньше К_m, тем больше их способность к образованию фермент-субстратного комплекса.

Характерной особенностью действия ферментов является также высокая чувствительность активности ферментов к внешним условиям – рН среды и температуре. Ферменты активны лишь в достаточно узком интервале рН и температуры, причем для ферментов характерно наличие в этом интервале максимума активности при некотором оптимальном значении рН или температуры; по обе стороны от этого значения активность ферментов быстро снижается.

Рис. 2.12. Зависимость скорости ферментативной реакции от концентрации субстрата.

ТЕРМОДИНАМИКА РАСТВОРОВ

Существование абсолютно чистых веществ невозможно – всякое вещество обязательно содержит примеси, или, иными словами, всякая гомогенная система многокомпонентна. Если имеющиеся в веществе примеси в пределах точности описания системы не оказывают влияния на изучаемые свойства, можно считать систему однокомпонентной; в противном случае гомогенную систему считают раствором.

Раствор – гомогенная система, состоящая из двух или более компонентов, состав которой может непрерывно изменяться в некоторых пределах без скачкообразного изменения её свойств.

Раствор может иметь любое агрегатное состояние; соответственно их разделяют на твердые, жидкие и газообразные (последние обычно называют газовыми смесями). Обычно компоненты раствора разделяют на растворитель и растворенное вещество. Как правило, растворителем считают компонент, присутствующий в растворе в преобладающем количестве либо компонент, кристаллизующийся первым при охлаждении раствора; если одним из компонентов раствора является жидкое в чистом виде вещество, а остальными – твердые вещества либо газы, то растворителем считают жидкость. С термодинамической точки зрения это деление компонентов раствора не имеет смысла и носит поэтому условный характер.

Одной из важнейших характеристик раствора является его состав, описываемый с помощью понятия концентрация раствора. Ниже дается определение наиболее распространенных способов выражения концентрации и формулы для пересчета одних концентраций в другие, где индексы А и В относятся соответственно к растворителю и растворенному веществу.

Молярная концентрация С – число молей ν_В растворенного вещества в одном литре раствора.

Нормальная концентрация N – число молей эквивалентов растворенного вещества (равное числу молей ν_В, умноженному на фактор эквивалентности f) в одном литре раствора.

Моляльная концентрация m – число молей растворенного вещества в одном килограмме растворителя.

Процентная концентрация ω – число граммов растворенного вещества в 100 граммах раствора.

(III.1)

(III.2)

(III.3)

Еще одним способом выражения концентрации является мольная доля X — отношение числа молей данного компонента к общему числу молей всех компонентов в системе.

(III.4)

🎦 Видео

Как выучить Химию с нуля за 10 минут? Принцип Ле-ШательеСкачать

Химическое равновесие. Константа равновесия. 10 класс.Скачать

Кинетический анализ сложных реакцийСкачать

Химическая кинетика. Скорость химической реакции | ХимияСкачать

Обратимость и необратимость химических реакций. Химическое равновесие. 1 часть. 9 класс.Скачать

Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать

Химическая кинетика / Скорость химической реакцииСкачать

Скорость химических реакций. 9 класс.Скачать

Порядок реакцииСкачать

Физическая химия #3. Первый, второй и третий порядки химической реакции. Времена полупревращенияСкачать

Обратимая реакция второго порядка || Вывод уравнения || Разбор задачи || КинетикаСкачать

Урок №2. Закон действующих масс. Кинетическое уравнение скорости химической реакции Beyond ChemistryСкачать

USMLE Step 1 - Фармакология: кинетика ферментов | уравнение Михаелиса - Ментена и не толькоСкачать

ЛЕКЦИЯ №5 || Химическая кинетика || Обратимые реакции, параллельные реакции (начало)Скачать

Химическое равновесие. Закон действующих масс.Скачать