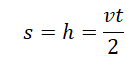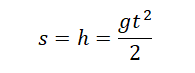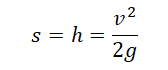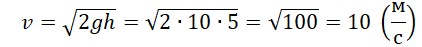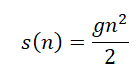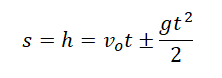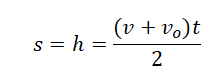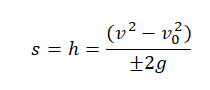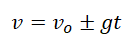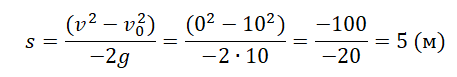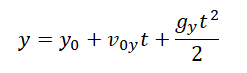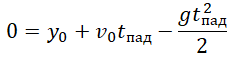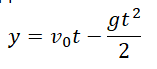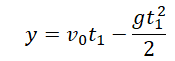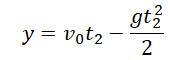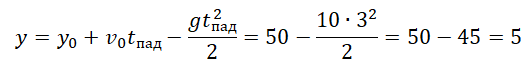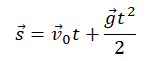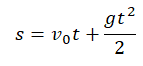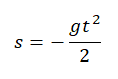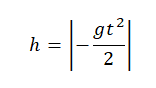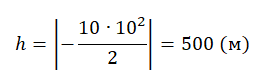Кинематического уравнения тела брошенного вверх (8 видео)

Содержание

Движение тела с ускорением свободного падения
теория по физике 🧲 кинематика
Ускорение свободного падения
Свободное падение
Движение тела, брошенного вертикально вверх
Уравнение координаты и скорости при свободном падении
Построение чертежа
Свободное падение на землю с некоторой высоты
Тело подбросили от земли и поймали на некоторой высоте
Тело подбросили от земли, на одной и той же высоте оно побывало дважды
Движение тела, брошенного вертикально вверх (вниз)
Движение тела, брошенного вертикально вверх
🔍 Видео

Видео:Теория движение тела брошенного вертикально вверхСкачать

Движение тела с ускорением свободного падения

теория по физике 🧲 кинематика

Свободное падение — это движение тела только под действием силы тяжести.

В действительности при падении на тело действует не только сила тяжести, но и сила сопротивления воздуха. Но в ряде задач сопротивлением воздуха можно пренебречь. Воздух не оказывает значимого сопротивления падающему мячу или тяжелому грузу. Но падение пера или листа бумаги можно рассматривать только с учетом двух сил: небольшая масса тела в сочетании с большой площадью его поверхности препятствует свободному падению вниз.

В вакууме все тела падают с одинаковым ускорением, так как в нем отсутствует среда, которая могла бы дать сопротивление. Так, брошенные в условиях вакуума с одинаковой высоты перо и молоток приземлятся в одно и то же время!

Видео:Физика 9 класс (Урок№1 - Движение тела, брошенного вертикально вверх)Скачать

Ускорение свободного падения

Ускорение свободного падения — векторная физическая величина. Вектор ускорения свободного падения всегда направлен вниз к центру Земли. Обозначается как g .

Единица измерения ускорения свободного падения — 1 м/с 2 .

Модуль ускорения свободного падения — скалярная величина. Обозначается как g. Численно равна 9,8 м/с 2 . При решении задач это значение округляется до целых: g = 10 м/с 2 .

Видео:Движение тела, брошенного вертикально вверх. Невесомость | Физика 9 класс #14 | ИнфоурокСкачать

Свободное падение

Свободное падение — частный случай равноускоренного прямолинейного движения. Если тело отпустить с некоторой высоты, оно будет падать с ускорением свободного падения без начальной скорости. Тогда его кинематические величины можно определить по следующим формулам:

v — скорость, g — ускорение свободного падения, t — время, в течение которого падало тело

Пример №1. Тело упало без начальной скорости с некоторой высоты. Найти его скорость в конечный момент времени t, равный 3 с.

Подставляем данные в формулу и вычисляем:

v = gt = 10∙3 = 30 (м/с).

Перемещение при свободном падении тела равно высоте, с которой оно начало падать. Высота обозначается буквой h.

Внимание! Перемещение равно высоте, с которой падало тело, только в том случае, если t — полное время падения.

Если известна скорость падения тела в момент времени t, перемещение (высота) определяется по следующей формуле.

Если скорость тела в момент времени t неизвестна, но для нахождения перемещения (высоты) используется формула:

Если неизвестно время, в течение которого падало тело, но известна его конечная скорость, перемещение (высота) вычисляется по формуле:

Пример №2. Тело упало с высоты 5 м. Найти его скорость в конечный момент времени.

Так как нам известна только высота, и найти нужно скорость, используем для вычислений последнюю формулу. Выразим из нее скорость:

Формула определения перемещения тела в n-ную секунду свободного падения:

s(n) — перемещение за секунду n.

Пример №3. Определить перемещение свободно падающего тела за 3-ую секунду движения.

Видео:Урок 37. Движение тела, брошенного под углом к горизонту (начало)Скачать

Движение тела, брошенного вертикально вверх

Движение тела, брошенного вертикально вверх, описывается в два этапа

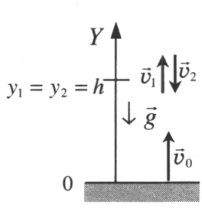
Два этапа движения тела, брошенного вертикально вверх Этап №1 — равнозамедленное движение. Тело поднимается вверх на некоторую высоту h за время t с начальной скоростью v₀ и на мгновение останавливается в верхней точке, достигнув скорости v = 0 м/с. На этом участке пути векторы скорости и ускорения свободного падения направлены во взаимно противоположных направлениях ( v ↑↓ g ). Этап №2 — равноускоренное движение. Когда тело достигает верхней точки, и его скорость равна 0, начинается свободное падение с начальной скоростью до тех пор, пока тело не упадет или не будет поймано на некоторой высоте. На этом участке пути векторы скорости и ускорения свободного падения направлены в одну сторону ( v ↑↑ g ). Формулы для расчета параметров движения тела, брошенного вертикально вверх Перемещение тела, брошенного вертикально вверх, определяется по формуле:

Если известна скорость в момент времени t, для определения перемещения используется следующая формула:

Если время движения неизвестно, для определения перемещения используется следующая формула:

Формула определения скорости:

Какой знак выбрать — «+» или «–» — вам помогут правила:

Если движение равнозамедленное (тело поднимается вверх), перед ускорением свободного падения в формуле нужно ставить знак «–», так как векторы скорости и ускорения противоположно направлены.
Если движение равноускоренное (тело падает вниз), перед ускорением свободного падения в формуле нужно ставить знак «+», так как векторы скорости и ускорения сонаправлены.

Обычно тело бросают вертикально вверх с некоторой высоты. Поэтому если тело упадет на землю, высота падения будет больше высоты подъема (h₂ > h₁). По этой же причине время второго этапов движения тоже будет больше (t₂ > t₁). Если бы тело приземлилось на той же высоте, то начальная скорость движения на 1 этапе была бы равно конечной скорости движения на втором этапе. Но так как точка приземления лежит ниже высоты броска, модуль конечной скорости 2 этапа будет выше модуля начальной скорости, с которой тело было брошено вверх (v₂ > v₀₁).

Пример №4. Тело подкинули вверх на некотором расстоянии 2 м от земли, придав начальную скорость 10 м/с. Найти высоту тела относительно земли в момент, когда оно достигнет верхней точки движения.

Конечная скорость в верхней точке равна 0 м/с. Но неизвестно время. Поэтому для вычисления перемещения тела с точки броска до верхней точки найдем по этой формуле:

Согласно условию задачи, тело бросили на высоте 2 м от земли. Чтобы найти высоту, на которую поднялось тело относительно земли, нужно сложить эту высоту и найденное перемещение: 5 + 2 = 7 (м).

Видео:Движение тела, брошенного вертикально вверхСкачать

Уравнение координаты и скорости при свободном падении

Уравнение координаты при свободном падении позволяет вычислять кинематические параметры движения даже в случае, если оно меняет свое направление. Так как при вертикальном движении тело меняет свое положение лишь относительно оси ОУ, уравнение координаты при свободном падении принимает

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Уравнение скорости при свободном падении:

Полезные факты

В момент падения тела на землю y = 0.
В момент броска тела от земли y₀ = 0.
Когда тело падает без начальной скорости (свободно) v₀ = 0.
Когда тело достигает наибольшей высоты v = 0.

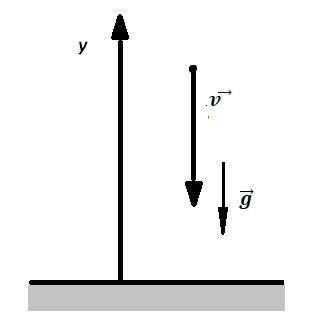
Построение чертежа

Решать задачи на нахождение кинематических параметров движения тела, брошенного вертикально вверх, проще, если выполнить чертеж. Строится он в 3 шага.

План построения чертежа

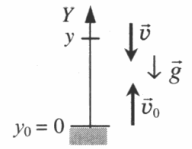
Чертится ось ОУ. Начало координат должно совпадать с уровнем земли или с самой нижней точки траектории.
Отмечаются начальная и конечная координаты тела (y и y₀).
Указываются направления векторов. Нужно указать направление ускорения свободного падения, начальной и конечной скоростей.

Свободное падение на землю с некоторой высоты

Тело подбросили от земли и поймали на некоторой высоте

Уравнение скорости:

Тело подбросили от земли, на одной и той же высоте оно побывало дважды

Интервал времени между моментами прохождения высоты h:

Уравнение координаты для первого прохождения h:

Уравнение координаты для второго прохождения h:

Важно! Для определения знаков проекций скорости и ускорения нужно сравнивать направления их векторов с направлением оси ОУ.

Пример №5. Тело падает из состояния покоя с высоты 50 м. На какой высоте окажется тело через 3 с падения?

Из условия задачи начальная скорость равна 0, а начальная координата — 50.

Через 3 с после падения тело окажется на высоте 5 м.

Алгоритм решения

Записать исходные данные.
Сделать чертеж, иллюстрирующий ситуацию.
Записать формулу для определения искомой величины в векторном виде.
Записать формулу для определения искомой величины в векторном виде.
Подставить известные данные и вычислить скорость.

Решение

Записываем исходные данные:

Перемещение (высота) свободно падающего тела, определяется по формуле:

В скалярном виде эта формула примет вид:

Учтем, что начальная скорость равна нулю, а ускорение свободного падения противоположно направлено оси ОУ:

Относительно оси ОУ груз совершил отрицательное перемещение. Но высота — величина положительная. Поэтому она будет равна модулю перемещения:

Вычисляем высоту, подставив известные данные:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Записать исходные данные.
Сделать чертеж, иллюстрирующий ситуацию.
Записать формулу для определения скорости тела в векторном виде.
Записать формулу для определения скорости тела в скалярном виде.
Подставить известные данные и вычислить скорость.

Решение

Записываем исходные данные:

Записываем формулу для определения скорости тела в векторном виде:

Теперь запишем эту формулу в скалярном виде. Учтем, что согласно чертежу, вектор скорости сонаправлен с осью ОУ, а вектор ускорения свободного падения направлен в противоположную сторону:

Подставим известные данные и вычислим скорость:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Видео:9 класс, 10 урок, Движение тела, брошенного вертикально вверхСкачать

Движение тела, брошенного вертикально вверх (вниз)

Начнем с утверждения, что

все тела на Земле, брошенные вертикально вверх, брошенные вертикально вниз и свободно падающие, — все они падают вниз или летят вверх с одним и тем же ускорением — ускорением свободного падения .

Надо сказать, что во всех трех случаях:

бросание тела вверх
бросание тела вниз
свободное падение тела

— во всех этих трех случаях ускорение свободного падения направлено исключительно вниз. Вертикально вниз.

В случае подбрасывания вверх движение тела — равнозамедленное (начальная скорость направлена вверх, ускорение — вниз — оно тормозит тело);
В случае бросания вниз движение тела — равноускоренное;
Также движение тела равноускоренное и в случае свободного падения с нулевой начальной скоростью.

Это утверждение бывает трудно воспринять. Жизнь нам показывает другое: камень и перышко падают по-разному. Камень падает быстро, а перышко спускается медленно. Никак нельзя сказать, что движение у них происходит с одним и тем же ускорением. Да, это так, но падение в этом случае — не свободное . Им мешает воздух. Есть такой классный опыт — трубка Галилея. В нем перышко и камень падают внутри трубки, из которой откачан воздух.

Движение там происходит действительно почти одинаково. Можете сами посмотреть видео .

Обратите внимание на то, что тела, подброшенные вертикально вверх, летят вверх с тем же ускорением свободного падения. Пока тело летит вверх, это ускорение направлено в сторону, противоположную движению. Оно замедляет движение вверх. Подброшенное вверх тело достигает верхней точки траектории и начинает падать вниз с тем же ускорением. Движение тела, брошенного вертикально вверх, — равноускоренное движение. При этом ускорение тела одинаково и направлено в сторону земли и тогда, когда тело летит вверх, и тогда, когда оно падает вниз.

Разбираться в этой теме лучше всего на конкретных задачах.

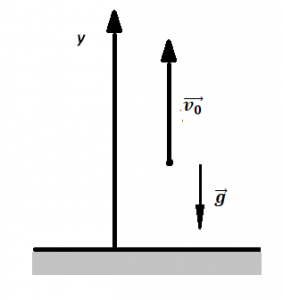
Шаг 1. Сделаем рисунок.

На рисунке обязательно надо указывать:

вектор ускорения свободного падения
ось для проектирования
вектор начальной скорости.

Шаг 2. Мы знаем, что движение происходит под действием ускорения свободного падения. То есть движение равноускоренное. Для равноускоренного движения мы знаем следующие формулы, которые описывают зависимость координаты от времени и проекции скорости от времени:

«Адаптируем» эти уравнения к нашему случаю. Что это значит? Запишем правильные значения начальной координаты x 0 x_0 x 0 , начальной скорости V 0 x V_ V 0 x и ускорения a x a_x a x .

Тогда наши формулы перепишутся в виде:

Или, если подставить числа и упростить:

Мы записали уравнения изменения координаты и проекции скорости.

Шаг 3. Теперь построим графики зависимости координаты и проекции скорости от времени.

Чтобы найти точки пересечения параболы с осью абсцисс, решим уравнение 2 t − 5 t 2 = 0 2t-5t^2=0 2 t − 5 t 2 = 0 :

Все нужное мы записали и построили.

Шаг 4. Предлагаем немного проанализировать полученные решения. Посмотрим на графики. Видно, что с увеличением времени координата сначала увеличивается — это наше тело подлетает наверх. Затем в момент времени 0 , 2 0,2 0 , 2 с тело достигает своей вершины — вершины параболы. Затем тело падает вниз и с увеличением времени координата все уменьшается и уменьшается.

Скорость. В начальный момент времени тело имело некоторую скорость. С увеличением времени (мы видим по графику) скорость все уменьшается, уменьшается и уменьшается, но ее проекция остается положительной. Это наше тело движется вверх. В верхней точке траектории тело «замирает» — скорость становится равной нулю. Затем тело начинает двигаться вниз. Скорость теперь уже направлена вниз — противоположно направлению оси O X OX O X . Поэтому проекция скорости становится отрицательной.

Последнее, что нам необходимо узнать в этой теме, — это значения координаты и скорости в некоторых особых точках. Это:

максимальная высота подъема
время подъема
время полета (до падения)
скорость в нижней точке траектории.

Удобнее всего рассмотреть конкретный пример.

б) максимальную высоту (относительно земли) h в е р ш и н ы h_ h в е р ш и н ы , на которую поднимается мячик;

в) скорость в момент пролета мячиком балкона при падении V б а л к о н V_ V б а л к о н ;

г) скорость в момент времени, когда мячик достигнет земли V з е м л я V_ V з е м л я .

Шаг 1. Прежде всего — сделаем рисунок, введем вертикальную ось.

Шаг 2. Запишем уравнения движения для нашего случая.

«Адаптируем» эти уравнения в общем виде к нашему конкретному случаю:

Подставим и числа тоже:

А теперь — самое главное (!).

Чтобы найти что-то в определенных точках траектории, нужно понять — чем эти точки отличаются от всех остальных точек траектории.

Найдем высоту подъема. Для этого подставим t в е р ш и н ы t_ t в е р ш и н ы в уравнение для координаты:

Мы справились с пунктами а) и б).

Точка пролета балкона и точка падения уникальны тем, что в них известны координаты. В точке пролета балкона y б а л к о н а = h = 1 y_=h=1 y б а л к о н а = h = 1 , а в нижней точке координата равна нулю: y з е м л я = 0 y_=0 y з е м л я = 0 .

Проекция скорости получилась отрицательной, поскольку мячик летел уже вниз. Обратите внимание: скорость точно такая же, как была при броске. Просто направлена уже в другую сторону. Так проявляет себя закон сохранения механической энергии, к которому мы обратимся немного позже.

Осталось найти скорость в момент времени, когда мячик достигнет земли. В нижней точке y з е м л я = 0 y_=0 y з е м л я = 0 . Используем этот факт и найдем время, за которое мячик достигнет земли:

У этого квадратного уравнения два корня: t 1 = − 0 , 2 t_1=-0,2 t 1 = − 0 , 2 и t 2 = 1 t_2=1 t 2 = 1 .

Первый момент времени нас не устраивает, поскольку он отрицательный. А второй — устраивает. Именно этот момент времени соответствует падению мячика на землю.

Найдем скорость в этот момент времени. Для этого подставим время t = 1 t=1 t = 1 в уравнение скорости V y = 4 − 1 0 t V_y=4-10t V y = 4 − 1 0 t :

Скорость получилась отрицательная, поскольку мячик летит вниз, а ось направлена вверх.

Еще раз резюме : чтобы найти какие-то величины в особых точках, нужно использовать их «особенности»; на вершине траектории скорость равна нулю, а в определенных точках траектории обычно известна координата тела.

Задачи для самостоятельного решения: #движение по вертикали

Видео:Физика. Движение тела, брошенного вертикально вверхСкачать

Движение тела, брошенного вертикально вверх

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Данный видеоурок предназначается для самостоятельного изучения темы «Движение тела, брошенного вертикально вверх». В ходе этого занятия учащиеся получат представление о движении тела, находящегося в свободном падении. Учитель расскажет о движении тела, брошенного вертикально вверх.