Кинематическое уравнение движения груза на нити (6 видео)

Кинематическое уравнение движения груза на нити

В эксперименте исследуется вращательное движение закрепленной на оси системы тел, у которой может меняться момент инерции. Различные моменты внешних сил создается грузами, подвешенными на нити, намотанной на шкив.

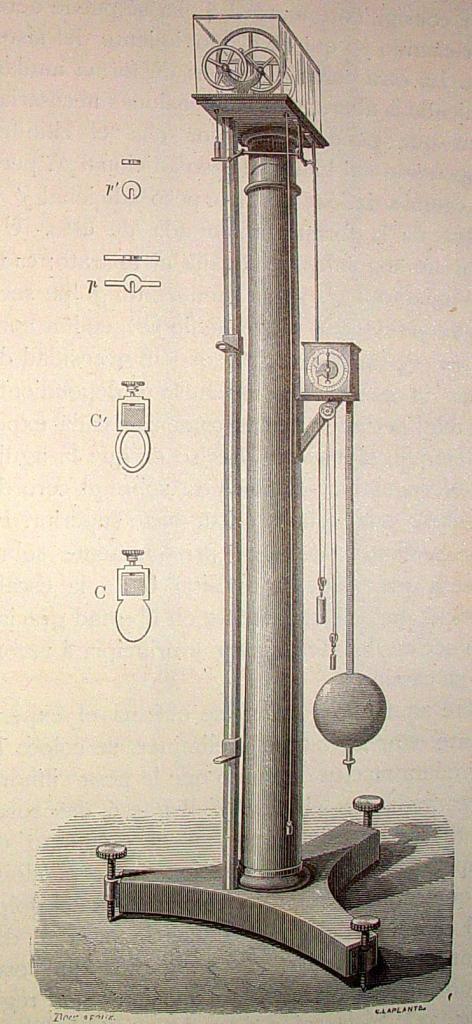
Основное уравнение вращательного движения твердого тела с моментом инерции J вокруг неподвижной оси z имеет вид (1.1)где — угловое ускорение, M — момент внешних сил.
Для экспериментального доказательства этого соотношения в работе используется маятник Обербека (рис.3). Он состоит из четырех стержней A и двух шкивов различного радиуса R₁ и R₂, укрепленных на одной горизонтальной оси. По стержням могут перемещаться и закрепляться в нужном положении четыре (по одному на каждом стержне) груза одинаковой массы m ‘ . При помощи груза массы m, прикрепленного к концу намотанной на тот или иной шкив нити, маятник может приводиться во вращение.
Пренебрегая силами трения и считая нить невесомой и нерастяжимой, можем написать: уравнение вращательного движения маятника (1.2)уравнение поступательного движения груза на нити (1.3)уравнение кинематической связи (1.4)Здесь R — радиус шкива, T — натяжение нити, a — линейное ускорение груза массы m, g — ускорение свободного падения.
Из системы уравнений (1.2-1.4) следует, что груз m должен двигаться с постоянным ускорением (1.5)Основное уравнение вращательного движения (1.1) было записано без учета момента сил трения в оси маятника и момента сил вязкого трения о воздух. Для доказательства правомерности такого подхода в процессе выполнения работы необходимо убедиться , что суммарный момент сил трения M_тр много меньше момента силы натяжения нити M , который равен: С учетом неравенства mR 2 J можно записать, что M 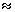mgR.
Оценить величину момента сил трения можно, если предположить, что он остается неизменным во время движения. При опускании груза m c отметки x₀ на полную длину нити до отметки x₃ и затем при последующем подъеме до отметки x₄ изменение его потенциальной энергии будет равно работе силы трения, то есть где Ф — полный угол поворота маятника Обербека. Причем поэтому Таким образом, условие малости момента сил трения окончательно имеет вид (1.6)

Установка для изучения вращательного движения (рис.4) или AVI (15.3M) состоит из основания (1), вертикальной колонны (2) с закрепленными на ней двумя подвижными кронштейнами (3,4), на которых крепятся оптические датчики положения. На колонне закреплены два неподвижных кронштейна (5,6).
На нижнем кронштейне (5) закреплен двухступенчатый вал (7). На верхнем кронштейне (6) закреплен подшипниковый узел (8) и блок (9). Через блок перекинута нить (10), один конец которой намотан на двухступенчатый вал (7), а на втором конце закреплен груз (11). На двухступенчатом валу крепятся тело маятника (12).
Кронштейны с фотодатчиками могут крепиться на разной высоте. Расстояние между этими кронштейнами измеряется по шкале, нанесенной на колонне. Время движения грузов определяют с помощью электронного таймера. Запуск таймера осуществляется нажатием кнопки «Пуск», остановка — кнопкой «Стоп». При подготовке к дальнейшим измерениям результаты предыдущих измерений убираются с табло таймера нажатием кнопки «Сброс».

Упражнение 1. Проверка закона движения.

Из (1.2-1.4) следует, что вращение маятника Обербека происходит с постоянным угловым ускорением 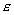, при этом груз m опускается с постоянным линейным ускорением a. Координата x груза, отпушенного без начальной скорости с отметки x₀ меняется по закону (ось х системы координат направлена вниз (см. рис. 3)) (1.7)Используя (1.7), определим время t пролета груза между двумя отметками x₁ и x₂: (1.8)Из (1.8) следует, что в случае равнопеременного движения (a=const) и фиксированных положений x₀ и, x₂ зависимость времени t от является линиейной и изображается на графике прямой линией.

Установить максимальное расстояние между кронштейнами с фотодатчиками
Установить грузы m ‘ в среднее положение, разместив их на равном расстоянии от оси таким образом, чтобы маятник находился в положении безразличного равновесия. Начало движения груза m всегда осуществляют от одного и того же положения x₀, которое необходимо записать в рабочий журнал. Нить наматывают на вал большего диаметра виток к витку.
Опустить груз m и произвести измерение времени t пролета груза m между фотодатчиками. Данные записать в таблицу 1.1 Провести измерения времени t для нескольких положений x₁ верхнего датчика (рекомендуется менять x₁ с шагом 5 см). Для каждого положения датчика измерения времени проводят не менее 3-х раз.
Для 5-7 первых опытов измерить значения x₄ — отметки, до которой поднимается груз при вращении маятника в одну сторону. Результаты занести в табл. 1.1.
Определить значение x₃ — максимальной отметки, до которой опускается груз m при своем движении.

Содержание

ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Изучение законов поступательного движения на машине Атвуда: формулы и пояснения
Что такое машина Атвуда?
Уравнения динамики
Расчет уравнений динамики для равноускоренного движения
Проверка решения уравнений динамики
Расчет силы тяжести
Определение силы натяжения нити
🔥 Видео

Таблица 1.1

N	x_1i	x₄	t_ij	S
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

Обработка результатов

По экспериментальным данным для каждого положения фотодатчика x₁ рассчитать среднее значение величины t_i по формуле

Кинематическое уравнение движения груза на нити

где N — число измерений при каждом фиксированном положении датчика.

Вычислить ошибку измерения (выборочное стандартное отклонение)

Результаты вычислений внести в табл. 1.1.

Построить зависимость t от , которая должна быть линиейной. Получившаяся линейная зависимость указывает на то, что движение тела является равнопеременным.
Найти среднее значение и оценить величину по формуле (1.6). Убедиться в малости момента сил трения по сравнению с начальным моментом силы натяжения нити.

Упражнение 2. Проверка независимости инерционных свойств маятника (момента инерции) от момента внешних сил.

В данном упражнении экспериментально показывается, что инерционные свойства маятника, а именно — момент инерции — не зависят от момента внешних сил.
Из уравнения (1.2) имеем (1.9)Из уравнений (1.5), (1.8) следует, что (1.10)В уравнение (1.10) входят величины, определяемые экспериментально.

Измерить штангенциркулем радиусы R₁ и R₂ шкивов, результаты, занести в рабочую тетрадь.
Устаноновить максимальное расстояние между кронштейнами с фотодатчиками. Занести в рабочий журнал координаты фотодатчиков x₁, x₂ и значение x₀.
Установить грузы m ‘ в среднее положение, разместив их на равном расстоянии от оси таким образом, чтобы маятник находился в положении безразличного равновесия.
На конец нити, намотанной на шкив радиуса R₁, прикрепить груз массы m₁ и измерить время прохождения груза между двумя фотодатчиками t. Одновременно измерить x₄— отметку, до которой поднимается груз. Измерение провести 3 раза. и результаты внести в табл.1.2.
Перебросить нить на другой шкив (радиуса R₂). и измерить время t и значение x₄ (3 раза). Результаты внести в табл. 1.2.
Провести аналогичные измерения (п.4-п.5), прикрепив к концу нити груз массы m₂. Результаты измерений занести в табл.1.2.

Таблица 1.2

Комбинации значений радиусов шкивов и масс при измерениях	N	t_ij	x₄	, S	J_i , S_{J_i}
R₁ , m₁	1
	2
	3
R₂ , m₁	4
	5
	6
R₁ , m₂	7
	8
	9
R₂ , m₂	10
	11
	12

Обработка результатов

По экспериментальным данным вычислить средние значения величин t и ошибки их измерений для четырех различных опытов. Результаты вычислений внесети в табл.1.2.
Вычислить значения моментов инерции J₁:J₄ по формуле (1.10).
Определить значение для каждого опыта.
Найти отношение аналогично тому, как это было сделано в упр.1. Результаты внести в табл. 1.2.
Произвести оценку погрешностей полученных результатов. В связи с тем, что экспериментальные значения J_i являются результатом косвенных измерений, то стандартное отклонение функции нескольких независимых переменных находится через ошибки прямых измерений по формуле для ошибки косвенных измерений.
Проанализировать полученный результат. Для этого отметить значения моментов инерции J₁:J₄ с учетом погрешностей на числовых осях (рис.5), выбирая J_i=S_{J_i}. Пересечение этих областей будет указывать на выполнение соотношения (1.9) , что свидетельствеут о независимости инерционных свойств маятника от момента внешних сил.

Упражнение 3. Проверка основного уравнения вращательного движения и теоремы Гюйгенса-Штейнера.

Пусть J₀ ‘ — суммарный момент инерции четырех грузов с массами M ‘ относительно осей, проходящих через их центры масс. При удалении центров грузов на расстояние l=l₁, от оси вращения (см. рис. 3), согласно теореме Гюйгенса — Штейнера , момент инерции будет равен J₁ ‘ (1.11)Если J₀ — момент инерции маятника без грузов, то полный момент инерции маятника будет равен (1.12)При удалении центров масс грузов на расстояние l₂ соответственно имеем (1.13)С учетом уравнений (1.2)-(1.4) и (1.10) зависимость квадрата времени пролета груза между двумя отметками x₁ и x₂ от расстояния центра грузов m ‘ от оси вращения l имеет вид (1.14)Если l₁>l₂ , то (1.15)Уравнения (1.14)-и (1.15) дают (1.16)где t₁ , t₂ — времена пролета груза между датчиками для случаев l=l₁ и l=l₂ соответственно.
В это уравнение входят величины, определяемые экспериментально.

На конец нити, намотанной на шкив радиуса R₂ (большего по размеру), прикрепить груз наибольшей массы. Фотодатчики оставить в том же положении, что и в упражнении 2.
Установить минимальное значение момента инерции маятника. Для этого грузы m ‘ установить в положение, наиболее близкое к оси. Измерить расстояние от грузов до оси. Занести это значение в табл 1.3.
Определить величину t. — время прохождения груза m между двумя фотодатчиками и x₄ — отметку, до которой он поднимается в процессе движения.Измерения проводят 3 раза. Результаты заносят в табл.1.3.
Изменяя положение грузов m ‘ на стержнях с шагом 3 см, каждый раз измеряют время t. Результаты измерения и соответствующие им расстояния l от оси маятника до центров грузов записать в табл.1.3 . Одновременно для каждого опыта измеряют и заносят в табл. 1.3 значения величины x₄ .

Таблица 1.3

N	( #t_ij )	x₄	, S	( t_i ) 2 , S_{( t_i ) 2}	l	l 2
1
2
3
.

Обработка результатов

По экспериментальным данным для каждого положения грузов m ‘ найти средние значения величин t_i.
Вычислить погрешности измерения t_i и ( t_i) 2 .
Построить график зависимости квадрата времени опускания груза ( t_i) 2 . от l 2 , — это должна быть прямая линия.
Проверить соотношение (1.16) для нескольких пар значений t 2 и l 2 .
Для каждого момента инерции определить и отношение . Убедиться в выполнении приближения .

Основные итоги работы
В результате выполнения работы должна быть осуществлена экспериментальная проверка выполнения основного уравнения вращательного движения — уравнения моментов. Должны быть проверены соотношения (1.9) и (1.16) и установлена линейная ( t) 2 зависимость от l 2 .
Контрольные вопросы

Что такое абсолютно твердое тело? Сколько степеней свободы имеет твердое тело? Сколько независимых скалярных уравнений требуется для описания движения твердого тела?

Почему угловая скорость является вектором? Куда направлен этот вектор?

Что такое момент силы относительно некоторой точки? Куда он направлен? Что такое момент силы относительно закрепленной оси?

Что такое момент импульса системы тел?

Что такое момент инерции тела относительно закрепленной оси?

Сформулируйте теорему Гюйгенса-Штейнера.

Как получить уравнение моментов и основное уравнение вращательного движения относительно закрепленной оси?

Литература

Матвеев А.Н. Механика и теория относительности. 2-е изд. М.: Высшая школа, 1986, § 31,32,34.

Сивухин Д.В. Общий курс физики. Том 1. Механика,3-е изд. M.: Наука.1989, § 30,35.

Видео:Два груза на нити, перекинутой через блок (Московкина 16.22)Скачать

ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА

Цель работы – экспериментальная проверка основного уравнения динамики вращательного движения твердого тела вокруг закрепленной оси.

Идея эксперимента

В эксперименте исследуется вращательное движение закрепленной на оси системы тел, у которой может меняться момент инерции (маятник Обербека). Различные моменты внешних сил создаются грузами, подвешенными на нити, намотанной на шкив.

Теоретическая часть

Основное уравнение динамики вращательного движения твердого тела с моментом инерции J вокруг неподвижной оси z имеет вид

, (9.1)

где – угловое ускорение, М – полный момент внешних сил. Поскольку величина e является функцией двух переменных, то изучение закона динамики вращательного движения твердого тела выполняется путем раздельного исследования двух зависимостей:

Рис. 23. Маятник Обербека

1) зависимости углового ускорения от момента силы при постоянном значении момента инерции (J = const);

2) зависимости углового ускорения от момента инерции при постоянном значении момента силы (M = const).

Полный момент внешних сил равен

, (9.2)

где М_н – вращающий момент (в данной работе — момент силы натяжения нити), М_тр – момент силы трения. С учетом этого основное уравнение динамики вращательного движения принимает вид линейной зависимости момента силы натяжения М_н от e:

. (9.3)

Для экспериментального доказательства справедливости этого соотношения в работе используется маятник Обербека (рис. 23). Он состоит из четырех стержней А и двух шкивов с различными радиусами R₁ и R₂, укрепленных на одной горизонтальной оси. По стержням могут перемещаться и закрепляться в нужном положении четыре цилиндрических груза (по одному на каждом стержне) одинаковой массы m₁. При помощи груза массы m, прикрепленного к концу нити, намотанной на тот или иной шкив, маятник может приводиться во вращение. Определяя продолжительность t движения и перемещение h груза, можно определить ускорение его поступательного движения

. (9.4)

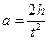
Это ускорение равно линейному ускорению точек шкива и связано с угловым ускорением крестовины соотношением

. (9.5)

Момент силы натяжения Т нити равен

. (9.6)

Силу Т можноопределить из второго закона Ньютона для поступательного движения, который в проекциях на ось 0Y дает

, (9.7)

Рис. 24. Зависимость момента силы натяжения нити от углового ускорения.

где m – масса груза.

Таким образом, момент сил натяжения нити равен

. (9.8)

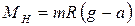
Согласно (9.3) М_н линейная функция e. На рис. 24 эти зависимости для различных значений моментов инерции системы изображены в виде графиков, угловые коэффициенты которых равны J. Эти графики отсекают от оси М_н отрезки, равные моменту силы трения М_тр. Так как М_тр одинаков во всех опытах, то все графики должны пересекаться в одной точке. Функция (9.3) верна для любых двух моментов сил, поэтому

(9.9)

. (9.10)

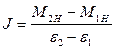
Таким образом, величина J может быть, с одной стороны, измерена, а с другой стороны, рассчитана, исходя из масс и геометрических размеров деталей установки Обербека. Момент инерции J маятника вычисляется из условия аддитивности момента инерции и равен сумме моментов инерции шкивов, крестовины и цилиндрических грузов, вращающихся вокруг оси, не проходящей через их середины. Графики позволяют также определить момент силы трения М_тр., действующей в системе.

Экспериментальная установка

Ось маятника Обербека закреплена в подшипниках, так что вся система может вращаться вокруг горизонтальной оси. Передвигая грузы по спицам, можно легко изменять момент инерции системы. На шкив виток к витку наматывается нить, к которой привязана платформа известной массы. На платформу накладываются грузы из набора. Высота падения грузов измеряется с помощью линейки, укрепленной параллельно нити. Маятник Обербека может быть снабжен электромагнитной муфтой – пускателем и электронным секундомером. Перед каждым опытом маятник следует тщательно отрегулировать. Особое внимание необходимо обратить на симметричность расположения грузов на крестовине. При этом маятник оказывается в состоянии безразличного равновесия.

Порядок выполнения работы

Задание 1. Оценка момента силы трения, действующей в системе.

1. Устанавливают грузы m₁ на крестовине в среднее положение, размещая их на равном расстоянии от оси таким образом, чтобы маятник находился в положении безразличного равновесия.

2. Накладывая небольшие грузы на платформу, определяют приближенно минимальную массу m₀, при которой маятник начнет вращаться. Оценивают момент силы трения из соотношения

, (9.11)

где R – радиус шкива, на который намотана нить.

3. Дальнейшие измерения желательно проводить с грузами массой .

Задание 2. Проверка основного уравнения динамики вращательного движения.

1. Укрепляют грузы m₁ на минимальном расстоянии от оси вращения. Балансируют маятник. Измеряют расстояние r от оси маятника до центров грузов.

2. Наматывают нить на один из шкивов. По масштабной линейке выбирают начальное положение платформы, производя отсчет, например, по ее нижнему краю. Тогда конечное положение груза будет находиться на уровне поднятой приемной платформы. Высота падения груза h равна разности этих отсчетов и может быть оставлена во всех опытах одинаковой.

3. Кладут на платформу первый груз. Расположив груз на уровне верхнего отсчета, фиксируют это положение, зажимая нить электромагнитной муфтой. Подготавливают к измерению электронный секундомер.

4. Отпускают нить, предоставив грузу возможность падать. Это достигается отключением муфты. При этом автоматически включается секундомер. Удар о приемную платформу останавливает падение груза и останавливает секундомер.

5. Измерение времени падения при одном и том же грузе выполняется не менее трех раз.

6. Проводят измерения времени падения груза m при других значениях момента М_н. Для этого либо добавляют на платформу дополнительные перегрузки, либо перебрасывают нить на другой шкив. При одном и том же значении момента инерции маятника необходимо провести измерения не менее чем с пятью значениями момента М_н.

7. Увеличивают момент инерции маятника. Для этого достаточно симметрично переместить грузы m₁ на несколько сантиметров. Шаг такого перемещения должен быть выбран таким образом, чтобы получить 5-6 значений момента инерции маятника. Проводят измерения времени падения груза m (п.2 – п.7). Все данные заносят в таблицу 1 отчета.

Обработка результатов. Исследование зависимости углового ускорения от момента силы при постоянном значении момента инерции.

1. Пользуясь формулами (9.4), (9.5), (9.8), определяют для каждого опыта по средним значениям времени значения линейного ускорения а, углового ускорения e и момента силы натяжения нити М_н.

2. Строят графики зависимостей момента силы М_н, как функции, от углового ускорения e, как аргумента, для различных моментов инерции маятника J. Т.к. М_н = f(e) – линейная функция, то ее графики будут прямыми линиями. Если экспериментальные точки не ложатся на прямую, графики надо проводить так, чтобы «разброс» точек был приблизительно одинаков по обе стороны прямой. При этом они не обязательно пройдут через одну точку на вертикальной оси. Малый «разброс» точек свидетельствует о хорошей линейности функции М_н = f(e) и том, что угловое ускорение действительно прямо пропорционально полному моменту сил, приложенных к вращающемуся телу.

Обработка результатов. Исследование зависимости углового ускорения от момента инерции при постоянном значении момента силы.

1. Для исследования используют ранее построенный график. Рассчитывают моменты инерции маятника по формуле (9.10). Для этого нужно выбирать точки прямо с графиков, например, А(М_1н,e₁)и В(М_2н,,e₂).

2. На графике проводят горизонтальную прямую через произвольную точку на оси М_н, пересекающую графики М_н = f(e). Точки пересечения позволяют определить те значения угловых ускорений маятника, которые соответствуют разным значениям моментов инерции, но при постоянном значении момента силы M = M_н – M_тр. Записывают полученные значения e и соответствующие им значения J в таблицу 2 отчета.

3. Угловое ускорение обратно пропорционально моменту инерции, т.е. график зависимости e = f(J) представляет собой гиперболу и не идентифицируется. Но график зависимости e = f(J -1 ) должен представлять собой прямую линию, проходящую через начало координат. Поэтому следует вычислить величины J -1 и построить соответствующий график. Угловой коэффициент наклона этого графика равен полному моменту приложенных сил.

Обработка результатов. Определение момента силы трения, действующей в системе.

1. В идеальном случае все графики M = f(e) должны пересекаться в одной точке, лежащей на оси М. Координата этой точки дает значение момента силы трения. Для реальных же графиков, скорее всего, будет иметь место некоторый разброс в положении этой точки.

2. Определить по графику все значения момента силы трения и найти его среднее значение. Сравнить полученный результат с ранее измеренным в задании 1.

Задание 3. Сравнение измеренных и вычисленных значений моментов инерции маятника.

1. Выписывают в таблицу 4 отчета измеренные значения моментов инерции маятника.

2. Используя формулы для расчета моментов инерции геометрически правильных тел и теорему Гюйгенса – Штейнера, вычисляют моменты инерции шкивов, крестовины и грузов, вращающихся вокруг оси, не проходящей через их середину. Данные для расчета берут из «паспорта» прибора. Общий момент инерции маятника находится суммированием моментов инерции деталей маятника.

3. Сравнивают вычисленные и измеренные значения моментов инерции. Находят относительные отклонения вычисленных и измеренных моментов инерции: .

Контрольные вопросы

1. Что называют моментом инерции материальной точки, твердого тела? Что называют моментом силы?

2. Запишите основное уравнение динамики вращательного движения.

3. Запишите кинематическое уравнение движения груза на нити.

4. Как связаны угловые и линейные кинематические величины?

5. Какая сила приводит во вращение маятник Обербека?

6. Запишите динамическое уравнение движения груза на нити.

7. Как рассчитать момент инерции маятника Обербека, используя данные эксперимента.

8. Сформулируйте теорему Гюйгенса-Штейнера.

9. Как рассчитать момент инерции маятника Обербека исходя из его геометрических размеров и формы?

Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

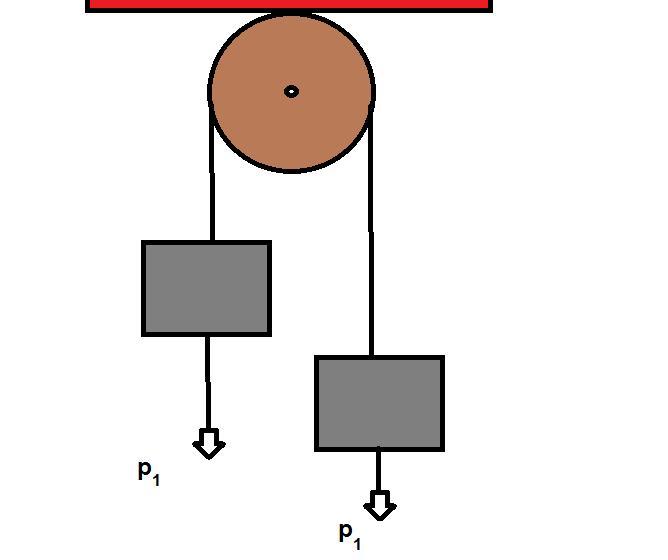
Изучение законов поступательного движения на машине Атвуда: формулы и пояснения

Использование простых механизмов в физике позволяет изучать различные природные процессы и законы. Одним из этих механизмов является машина Атвуда. Рассмотрим в статье, что она собой представляет, для чего используется, и какие формулы описывают принцип ее работы.

Видео:Никанорова Е. А. - Механика. Семинары - Кинематические связиСкачать

Что такое машина Атвуда?

Названная машина представляет собой простой механизм, состоящий из двух грузов, которые соединены переброшенной через неподвижный блок нитью (веревкой). В данном определении следует пояснить несколько нюансов. Во-первых, массы грузов в общем случае являются разными, что обеспечивает наличие у них ускорения под действием силы тяжести. Во-вторых, нить, связывающая грузы, считается невесомой и нерастяжимой. Эти предположения значительно облегчают последующие расчеты уравнений движения. Наконец, в-третьих, неподвижный блок, через который переброшена нить, также считается невесомым. Кроме того, во время его вращения пренебрегают силой трения. Ниже на схематическом рисунке показана эта машина.

Вам будет интересно: Пространственная экономика: описание специальностей и структура

Вам будет интересно: Что такое подполье? Подпольная организация «Молодая гвардия». Антифашистское движение

Машина Атвуда была изобретена английским физиком Джорджем Атвудом в конце XVIII века. Служит она для изучения законов поступательного движения, точного определения ускорения свободного падения и экспериментальной проверки второго закона Ньютона.

Видео:Физика На шнуре, перекинутом через неподвижный блок, подвешены грузы массами 0,3 и 0,2 кг. С какимСкачать

Уравнения динамики

Каждый школьник знает, что ускорение у тел появляется только в том случае, если на них оказывают действие внешние силы. Данный факт был установлен Исааком Ньютоном в XVII веке. Ученый изложил его в следующем математическом виде:

Где m – инерционная масса тела, a – ускорение.

Изучение законов поступательного движения на машине Атвуда предполагает знание соответствующих уравнений динамики для нее. Предположим, что массы двух грузов равны m1 и m2, причем m1>m2. В таком случае первый груз будет перемещаться вниз под действием силы тяжести, а второй груз будет двигаться вверх под действием силы натяжения нити.

Рассмотрим, какие силы действуют на первый груз. Их две: сила тяжести F1 и сила натяжения нити T. Силы направлены в разных направлениях. Учитывая знак ускорения a, с которым перемещается груз, получаем следующее уравнение движения для него:

Что касается второго груза, то на него действуют силы той же природы, что и на первый. Поскольку второй груз движется с ускорением a, направленным вверх, то уравнение динамики для него принимает вид:

Таким образом, мы записали два уравнения, в которых содержатся две неизвестных величины (a и T). Это означает, что система имеет однозначное решение, которое будет получено далее в статье.

Видео:Физика.Решение задач.Выполнялка 1Скачать

Расчет уравнений динамики для равноускоренного движения

Как мы видели из записанных выше уравнений, результирующая сила, действующая на каждый груз, остается неизменной в процессе всего движения. Масса каждого груза также не меняется. Это означает, что ускорение a будет постоянным. Такое движение называют равноускоренным.

Изучение равноускоренного движения на машине Атвуда заключается в определении этого ускорения. Запишем еще раз систему динамических уравнений:

Чтобы выразить значение ускорения a, сложим оба равенства, получаем:

F1 – F2 = a*(m1 + m2) =>

a = (F1 – F2)/(m1 + m2).

Подставляя явное значение сил тяжести для каждого груза, получаем конечную формулу для определения ускорения:

a = g*(m1 – m2)/(m1 + m2).

Отношение разницы масс к их сумме называют числом Атвуда. Обозначим его na, тогда получим:

Видео:Траектория и уравнения движения точки. Задача 1Скачать

Проверка решения уравнений динамики

Выше мы определили формулу для ускорения машины Атвуда. Она является справедливой только в том случае, если справедлив сам закон Ньютона. Проверить этот факт можно на практике, если провести лабораторную работу по измерению некоторых величин.

Лабораторная работа с машиной Атвуда является достаточно простой. Суть ее заключается в следующем: как только грузы, находящиеся на одном уровне от поверхности, отпустили, необходимо засечь время движения грузов секундомером, а затем, измерить расстояние, на которое переместился любой из грузов. Предположим, что соответствующие время и расстояние равны t и h. Тогда можно записать кинематическое уравнение равноускоренного движения:

Откуда ускорение определяется однозначно:

Отметим, что для увеличения точности определения величины a, следует проводить несколько экспериментов по измерению hi и ti, где i – номер измерения. После вычисления значений ai, следует рассчитать среднюю величину acp из выражения:

Где m – количество измерений.

Приравнивая это равенство и полученное ранее, приходим к следующему выражению:

Если данное выражение оказывается справедливым, то таковым также будет и второй закон Ньютона.

Видео:Вращательное движение. 10 класс.Скачать

Расчет силы тяжести

Выше мы предположили, что значение ускорения свободного падения g нам известно. Однако при помощи машины Атвуда определение силы тяжести также оказывается возможным. Для этого вместо ускорения a из уравнений динамики следует выразить величину g, имеем:

Чтобы найти g, следует знать, чему равно ускорение поступательного перемещения. В пункте выше мы уже показали, как его находить экспериментальным путем из уравнения кинематики. Подставляя формулу для a в равенство для g, имеем:

Вычислив значение g, несложно определить силу тяжести. Например, для первого груза ее величина будет равна:

Видео:Два тела связанные нитью и неподвижный блокСкачать

Определение силы натяжения нити

Сила T натяжения нити является одним из неизвестных параметров системы динамических уравнений. Выпишем еще раз эти уравнения:

Если в каждом равенстве выразить a, и приравнять оба выражения, тогда получим:

(F1 – T)/m1 = (T – F2)/m2 =>

T = (m2*F1 + m1*F2)/(m1 + m2).

Подставляя явные значения сил тяжести грузов, приходим к конечной формуле для силы натяжения нити T:

T = 2*m1*m2*g/(m1 + m2).

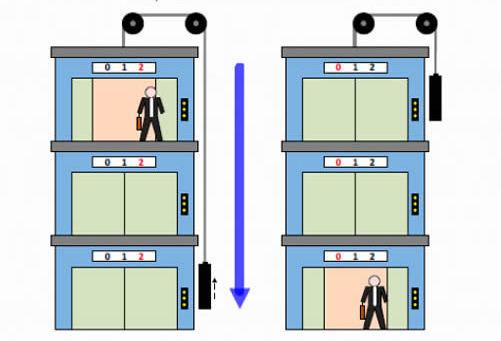
Машина Атвуда имеет не только теоретическую пользу. Так, подъемник (лифт) использует при своей работе контргруз с целью подъема на высоту полезного груза. Такая конструкция значительно облегчает работу двигателя.