Теоретическая механика:
Вращательное движение твердого тела

Смотрите также решения задач по теме «Вращательное движение» в онлайн решебниках Яблонского, Мещерского, Чертова (с примерами и методичкой для заочников), Иродова и Савельева.

При поступательном движении тела (§ 60 в учебнике Е. М. Никитина) все его точки движутся по одинаковым траекториям и в каждый данный момент они имеют равные скорости и равные ускорения.

Поэтому поступательное движение тела задают движением какой-либо одной точки, обычно движением центра тяжести.

Рассматривая в какой-либо задаче движение автомобиля (задача 147) или тепловоза (задача 141), фактически рассматриваем движение их центров тяжести.

Вращательное движение тела (Е. М. Никитин, § 61) нельзя отождествить с движением какой-либо одной его точки. Ось любого вращающегося тела (маховика дизеля, ротора электродвигателя, шпинделя станка, лопастей вентилятора и т. п.) в процессе движения занимает в пространстве относительно окружающих неподвижных тел одно и то же место.

Движение материальной точки или поступательное движение тела характеризуют в зависимости от времени линейные величины s (путь, расстояние), v (скорость) и а (ускорение) с его составляющими a_t и a_n.

Вращательное движение тела в зависимости от времени t характеризуют угловые величины : φ (угол поворота в радианах), ω (угловая скорость в рад/сек) и ε (угловое ускорение в рад/сек 2 ).

Закон вращательного движения тела выражается уравнением
φ = f (t).

Угловая скорость – величина, характеризующая быстроту вращения тела, определяется в общем случае как производная угла поворота по времени
ω = dφ/dt = f’ (t).

Угловое ускорение – величина, характеризующая быстроту изменения угловой скорости, определяется как производная угловой скорости
ε = dω/dt = f» (t).

Приступая к решению задач на вращательное движение тела, необходимо иметь в виду, что в технических расчетах и задачах, как правило, угловое перемещение выражается не в радианах φ, а в оборотах φ_об.

Поэтому необходимо уметь переходить от числа оборотов к радианному измерению углового перемещения и наоборот.

Так как один полный оборот соответствует 2π рад, то
φ = 2πφ_об и φ_об = φ/(2π).

Угловая скорость в технических расчетах очень часто измеряется в оборотах, произведенных в одну минуту (об/мин), поэтому необходимо отчетливо уяснить, что ω рад/сек и n об/мин выражают одно и то же понятие – скорость вращения тела (угловую скорость), но в различных единицах – в рад/сек или в об/мин.

Переход от одних единиц угловой скорости к другим производится по формулам
ω = πn/30 и n = 30ω/π.

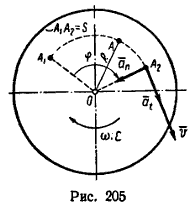
При вращательном движении тела все его точки движутся по окружностям, центры которых расположены на одной неподвижной прямой (ось вращающегося тела). Очень важно при решении задач, приведенных в этой главе, ясно представлять зависимость между угловыми величинами φ, ω и ε, характеризующими вращательное движение тела, и линейными величинами s, v, a_t и a_n, характеризующими движение различных точек этого тела (рис 205).

Если R – расстояние от геометрической оси вращающегося тела до какой-либо точки А (на рис. 205 R=OA), то зависимость между φ – углом поворота тела и s – расстоянием, пройденным точкой тела за то же время, выражается так:
s = φR.

Зависимость между угловой скоростью тела и скоростью точки в каждый данный момент выражается равенством
v = ωR.

Касательное ускорение точки зависит от углового ускорения и определяется формулой
a_t = εR.

Нормальное ускорение точки зависит от угловой скорости тела и определяется зависимостью
a_n = ω 2 R.

При решении задачи, приведенной в этой главе, необходимо ясно понимать, что вращением называется движение твердого тела, а не точки. Отдельно взятая материальная точка не вращается, а движется по окружности – совершает криволинейное движение.

Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

§ 33. Равномерное вращательное движение

Если угловая скорость ω=const, то вращательное движение называется равномерным.

Уравнение равномерного вращения имеет вид
φ = φ₀ + ωt.

В частном случае, когда начальный угол поворота φ₀=0,
φ = ωt.

Угловую скорость равномерно вращающегося тела
ω = φ/t
можно выразить и так:
ω = 2π/T,
где T – период вращения тела; φ=2π – угол поворота за один период.

Видео:Вращательное движение. 10 класс.Скачать

§ 34. Равнопеременное вращательное движение

Вращательное движение с переменной угловой скоростью называется неравномерным (см. ниже § 35). Если же угловое ускорение ε=const, то вращательное движение называется равнопеременным . Таким образом, равнопеременное вращение тела – частный случай неравномерного вращательного движения.

Уравнение равнопеременного вращения
(1) φ = φ₀ + ω₀t + εt 2 /2
и уравнение, выражающее угловую скорость тела в любой момент времени,
(2) ω = ω₀ + εt
представляют совокупность основных формул вращательного равнопеременного движения тела.

В эти формулы входят всего шесть величин: три постоянных для данной задачи φ₀, ω₀ и ε и три переменных φ, ω и t. Следовательно, в условии каждой задачи на равнопеременное вращение должно содержаться не менее четырех заданных величин.

Для удобства решения некоторых задач из уравнений (1) и (2) можно получить еще две вспомогательные формулы.

Исключим из (1) и (2) угловое ускорение ε:
(3) φ = φ₀ + (ω + ω₀)t/2.

Исключим из (1) и (2) время t:
(4) φ = φ₀ + (ω 2 — ω₀ 2 )/(2ε).

В частном случае равноускоренного вращения, начавшегося из состояния покоя, φ₀=0 и ω₀=0. Поэтому приведенные выше основные и вспомогательные формулы принимают такой вид:
(5) φ = εt 2 /2;
(6) ω = εt;
(7) φ = ωt/2;
(8) φ = ω 2 /(2ε).

Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

§ 35. Неравномерное вращательное движение

Рассмотрим пример решения задачи, в которой задано неравномерное вращательное движение тела.

Видео:Кинематика вращательного движения. ТермехСкачать

Вращательное движение тела. Закон вращательного движения

В этой статье описывается важный раздел физики — «Кинематика и динамика вращательного движения».

Видео:Основные понятия и уравнения кинематики равноускоренного движения тела.Скачать

Основные понятия кинематики вращательного движения

Вращательным движением материальной точки вокруг неподвижной оси называют такое движение, траекторией которого является окружность, находящаяся в плоскости перпендикулярной к оси, а центр ее лежит на оси вращения.

Вращательное движение твердого тела — это движение, при котором по концентрическим (центры которых лежат на одной оси) окружностям движутся все точки тела в соответствии с правилом для вращательного движения материальной точки.

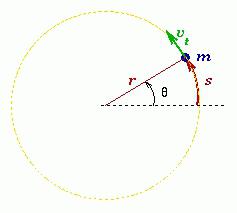
Пусть произвольное твердое тело T совершает вращения вокруг оси O, которая перпендикулярна плоскости рисунка. Выберем на данном теле точку M. При вращении эта точка будет описывать вокруг оси O круг радиусом r.

Через некоторое время радиус повернется относительно исходного положения на угол Δφ.

За положительное направление поворота принято направление правого винта (по часовой стрелке). Изменение угла поворота со временем называется уравнением вращательного движения твердого тела:

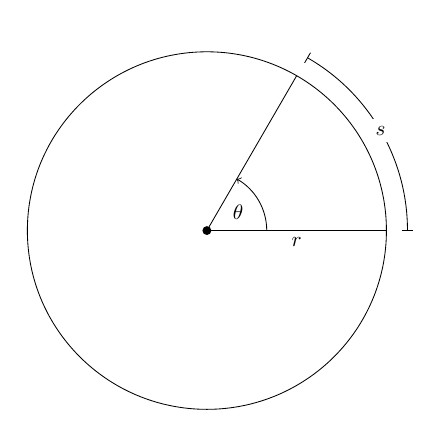
Если φ измерять в радианах (1 рад — это угол, соответствующий дуге, длиной равной ее радиусу), то длина дуги окружности ΔS, которую пройдет материальная точка M за время Δt, равна:

Видео:Кинематика. Закон движения. Урок 3Скачать

Основные элементы кинематики равномерного вращательного движения

Мерой перемещения материальной точки за небольшой промежуток времени dt служит вектор элементарного поворота dφ.

Угловая скорость материальной точки или тела — это физическая величина, которая определяется отношением вектора элементарного поворота к продолжительности этого поворота. Направление вектора можно определить правилом правого винта вдоль оси О. В скалярном виде:

Если ω = dφ/dt = const, то такое движение называется равномерное вращательное движение. При нем угловую скорость определяют по формуле

Согласно предварительной формуле размерность угловой скорости

Равномерное вращательное движение тела можно описать периодом вращения. Период вращения T — физическая величина, определяющая время, за которое тело вокруг оси вращения выполняет один полный оборот ([T] = 1 с). Если в формуле для угловой скорости принять t = T, φ = 2 π (полный один оборот радиуса r), то

поэтому период вращения определим следующим образом:

Число оборотов, которое за единицу времени совершает тело, называется частотой вращения ν, которая равна:

Единицы измерения частоты: [ν]= 1/c = 1 c -1 = 1 Гц.

Сравнивая формулы для угловой скорости и частоты вращения, получим выражение, связывающее эти величины:

Видео:Вращательное движение твёрдого тела. Задачи 1, 2, 3Скачать

Основные элементы кинематики неравномерного вращательного движения

Неравномерное вращательное движение твердого тела или материальной точки вокруг неподвижной оси характеризует его угловая скорость, которая изменяется со временем.

Вектор ε, характеризующий скорость изменения угловой скорости, называется вектором углового ускорения:

Если тело вращается, ускоряясь, то есть dω/dt > 0, вектор имеет направление вдоль оси в ту же сторону, что и ω.

Если вращательное движение замедлено — dω/dt 2 /r = ω 2 r 2 /r.

Итак, в скалярном виде

Тангенциальное ускоренной материальной точки, которая выполняет вращательное движение

Видео:Физика. 10 класс. Задачи на вращательное движениеСкачать

Момент импульса материальной точки

Векторное произведение радиуса-вектора траектории материальной точки массой m_i на ее импульс называется моментом импульса этой точки касательно оси вращения. Направление вектора можно определить, воспользовавшись правилом правого винта.

Момент импульса материальной точки (L_i) направлен перпендикулярно плоскости, проведенной через r_i и υ_i, и образует с ними правую тройку векторов (то есть при движении с конца вектора r_i к υ_i правый винт покажет направление вектора L_i).

В скалярной форме

Учитывая, что при движении по кругу радиус-вектор и вектор линейной скорости для i-й материальной точки взаимно перпендикулярные,

Так что момент импульса материальной точки для вращательного движения примет вид

Видео:Урок 89 (осн). Задачи на вращательное движение - 1Скачать

Момент силы, которая действует на i-ю материальную точку

Векторное произведение радиуса-вектора, который проведен в точку приложения силы, на эту силу называется моментом силы, действующей на i-ю материальную точку относительно оси вращения.

В скалярной форме

Величина l_i, равная длине перпендикуляра, опущенного из точки вращения на направление действия силы, называется плечом силы F_i.

Видео:Поступательное и вращательное движенияСкачать

Динамика вращательного движения

Уравнение динамики вращательного движения записывается так:

Формулировка закона следующая: скорость изменения момента импульса тела, которое совершает вращение вокруг неподвижной оси, равна результирующему моменту относительно этой оси всех внешних сил, приложенных к телу.

Видео:Вращательное движение. Практическая часть. 10 класс.Скачать

Момент импульса и момент инерции

Известно, что для i-й материальной точки момент импульса в скалярной форме задается формулой

Если вместо линейной скорости подставить ее выражение через угловую:

то выражение для момента импульса примет вид

Величина I_i = m_ir_i 2 называется моментом инерции относительно оси i-й материальной точки абсолютно твердого тела, проходящей через его центр масс. Тогда момент импульса материальной точки запишем:

Момент импульса абсолютно твердого тела запишем как сумму моментов импульса материальных точек, составляющих данное тело:

Видео:Урок 7. Механическое движение. Основные определения кинематики.Скачать

Момент силы и момент инерции

Закон вращательного движения гласит:

Известно, что представить момент импульса тела можно через момент инерции:

Учитывая, что угловое ускорение определяется выражением

получим формулу для момента силы, представленного через момент инерции:

Замечание. Момент силы считается положительным, если угловое ускорение, которым он вызван, больше нуля, и наоборот.

Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Теорема Штейнера. Закон сложения моментов инерции

Если ось вращения тела через центр масс его не проходит, то относительно этой оси можно найти его момент инерции по теореме Штейнера:
I = I₀ + ma 2 ,

где I₀ — начальный момент инерции тела; m — масса тела; a — расстояние между осями.

Если система, которая совершает обороты округ неподвижной оси, состоит из n тел, то суммарный момент инерции такого типа системы будет равен сумме моментов, ее составляющих (закон сложения моментов инерции).

Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Кинематика вращения

1.Уравнение вращения твердого тела: j= 4t 3 + 3t (рад). Угловая скорость через 2 с после начала вращения равна…

Варианты ответа: 12 рад/с 19 рад/с 51 рад/с 48 рад/с

2.Кинематический закон вращательного движения тела задан уравнением j=сt 2 , где c=1 рад/с2. Угловая скорость тела в конце третьей секунды равна…

Варианты ответа: 3 рад/с 4 рад/с 9 рад/с 6 рад/с

3.Тело вращается по закону j=17t 3 . Его угловое ускорение через 1 с от начала движения равно…

Варианты ответа: 17 рад/ с 2 51 рад/ с 2 102 рад/ с 2 68 рад/с 2

1. Диск вращается вокруг неподвижной оси, при этом угол поворота j меняется по закону: j=(2t 2 -t) , где j — в радианах, t – в секундах. Диск остановится в момент времени…

Варианты ответаа. 0 с; б. 0,25 с; в. 0,5 с; г. 4 с.

1. Частица движется вдоль окружности радиусом 1 м в соответствии с уравнением , где – в радианах, t – в секундах. Частица остановится в момент времени (в с), равный…

Варианты ответа: 4 1 3 2

1. Частица движется из состояния покоя по дуге радиусом 2 м с угловой скоростью изменяющейся по закону . Отношение нормального ускорения с касательному через 2с равно…

Варианты ответа 8 3 2 1

1. Диск вращается вокруг неподвижной оси, при этом угол поворота j меняется по закону: j=(2t 2 -t) (j — в радианах, t – в секундах). Угловая скорость и угловое ускорение диска в момент времени t=2c равны…

Варианты ответа:а. 7 (рад/с), 3 (рад/с 2 ); б. 8 (рад/с), 3 (рад/с 2 );

в. 7 (рад/с), 4 (рад/с 2 ); г. 4 (рад/с), 4 (рад/с 2 ).

1. Тело вращается вокруг неподвижной оси по закону j =-3t 2 +30t + 15. Найти величину углового ускорения для момента времени 4 с

Варианты ответа: а. 24 рад/с 2 б. – 6 рад/с 2 в. 6 рад/с 2 г. -24 рад/с 2

1. Угол поворота вала изменяется по закону j = t 2 + 5t + 8. При этом угловое ускорение вала составляет…

Варианты ответа: а. 2 1/с 2 б. 5 1/с 2 в. 8 1/с 2 г. 0

10. Диск радиуса R вращается вокруг вертикальной оси равноускоренно по часовой стрелке. Укажите направление вектора углового ускорения.

Варианты ответа: 2 4 1 3

11.Диск радиуса R вращается вокруг вертикальной оси равноускоренно с заданным направлением вектора углового ускорения. Укажите направление вектора линейной скорости точки А, лежащей на ободе диска.

Варианты ответа: 2 4 1 3

1. Диск радиуса Rвращается вокруг вертикальной оси равноускоренно против часовой стрелки. Укажите направление вектора угловой скорости.
   Варианты ответа:

а. 1; б. 2; в. 3; г. 4.

13.Диск вращается равноускоренно вокруг горизонтальной оси. Укажите направление вектора углового ускорения точки А на ободе диска.

Варианты ответа: 2 4 1 3

14.Диск вращается равноускоренно вокруг горизонтальной оси. Укажите направление вектора тангенциального ускорения точки А на ободе диска

Варианты ответа: а. 1 б. 2 в. 3 г. 4

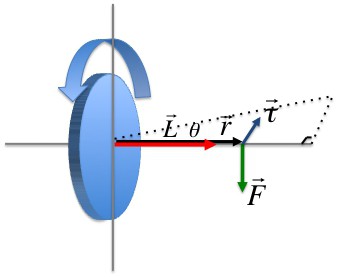
15. Колесо вращается так, как показано на рис. белой стрелкой. К ободу колеса приложена сила, направленная по касательной. Правильно изображает угловое перемещение вектор…

Варианты ответа: а. 1 б. 2 в. 3 г. 4 д. 5

16.Диск вращается вокруг своей оси, изменяя проекцию своей угловой скорости так, как показано на рисунке. Вектор угловой скорости и вектор углового ускорения направлены в одну сторону в интервалы времени …

Варианты ответа:

всегда направлены в одну сторону

1. Диск вращается вокруг своей оси, изменяя проекцию своей угловой скорости w_z(t) так, как показано на рисунке. Вектор углового ускорения направлен в ту же сторону, что и ось Z в интервалы времени

18. Диск вращается вокруг своей оси, изменяя проекцию своей угловой скорости так, как показано на рисунке. Величина углового перемещения максимальна в промежутки времени: …

б. от 0 до t ₁ и от t ₁ до t ₂

в. перемещение одинаково за все промежутки времени

г. от 0 до t ₁ и от t ₂ до t ₃

19. Диск вращается вокруг своей оси, изменяя проекцию своей угловой скорости w_z(t) так, как показано на рисунке. Если в момент времени t₁=1с величина угловой скорости 10 рад/с, а в момент времени t₃=3с — -10 рад/с, то вектор углового ускорения в этот промежуток времени имеет модуль и направление:…

а. 10 рад/с 2 , вдоль оси z б. 5 рад/с 2 , вдоль оси z

в. 10 рад/с 2 , противоположно оси z г. 5 рад/с 2 , противоположно оси z

1. Точка движется по окружности с угловой скоростью, изменяющейся в соответствии с графиком. Укажите верное утверждение для нормального а_n и тангенциального a_t ускорений этой точки.
   Варианты ответа:

а. а_n — увеличивается, a_t — уменьшается;

б. а_n — постоянно, a_t — постоянно;

в. а_n — постоянно, a_t — увеличивается;

г. а_n — увеличивается, a_t — увеличивается;

д. а_n — увеличивается, a_t — постоянно.

21. На рисунке представлен график зависимости угловой скорости w(t) вращающегося тела от времени. Угловое ускорение за вторую секунду равно…

10 с -2 15 с -2 20 с -2 30 с -2 25 с -2

1. Угловая скорость изменяется так, как показано на рисунке. Определить величину угла поворота через 6 с.

а. 30 рад б. 24 рад в. 60 рад г. 12 рад д. 36 рад

23. Тело вращается вокруг неподвижной оси. Зависимость угловой скорости от времени приведена на рисунке. Тангенциальное ускорение точки, находящейся на расстоянии 1 м от оси вращения, равно.

0,5 м/с 2 -5 м/с 2 -0,5 м/с 2 5 м/с 2

1. Твердое тело из состояния покоя начинает вращаться вокруг оси Z с угловым ускорением, проекция которого изменяется во времени, как показано на графике. Угловая скорость вращения тела достигнет максимальной по модулю величины в момент времени, равный …

а. 2 с; б. 3 с; в. 5 с; г. 10 с.

1. Твердое тело из состояния покоя начинает вращаться вокруг оси Z с угловым ускорением, проекция которого изменяется во времени, как показано на графике. Угловая скорость вращения тела в момент времени 3 с, будет равна (в рад/с)…

а. 0; б. 2; в. 3; г. 6.

1. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на рисунке. Через 11 с тело окажется повернутым относительно начального положения на угол:

Варианты ответа: а. 8 рад б. 0 рад в. 12 рад г. 24 рад

1. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на рисунке. За все время движения тело может повернуться относительно начального положения на максимальный угол:

Варианты ответа: а. 8 рад б. 0 рад в. 12 рад г. 24 рад

1. Диск радиуса R начинает вращаться из состояния покоя в горизонтальной плоскости вокруг оси Z, проходящей перпендикулярно его плоскости через его центр. Зависимость проекции углового ускорения от времени показана на графике. Тангенциальные ускорения точки на краю диска в моменты времени t₁=2c и t₂=7c…..

а. отличаются в 4 раза б. равны нулю в. отличаются в 2 раза г. равны друг другу, но не равны нулю

1. Угловое ускорение характеризует.

а. Быстроту изменения положения точки.

б. Быстроту изменения величины скорости.

в. Быстроту изменения вектора скорости.

г. Быстроту изменения угловой скорости.

д. Быстроту изменения скорости по направлению.

30. Колесо вращается так, как показано на рисунке белой стрелкой. К ободу колеса приложена сила, направленная по касательной. Правильно изображает угловую скорость вектор

Варианты ответа: а. 1 б. 2 в. 3 г. 4 д. 5

31. Колесо вращается так, как показано на рисунке белой стрелкой. К ободу колеса приложена сила, направленная по касательной. Правильно изображает тангенциальное ускорение колеса вектор…

Варианты ответа: а. 1 б. 2 в. 3 г. 4 д. 5

32. Колесо вращается так, как показано на рисунке белой стрелкой. К ободу колеса приложена сила, направленная по касательной. Правильно изображает угловое перемещение скорость вектор

Варианты ответа: а. 1 б. 2 в. 3 г. 4 д. 5

Варианты ответа: а. 1 б. 2 в. 3 г. 4 д. 5

33. Материальная точка вращается по окружности. Зависимость величины углового перемещения от времени изображена на рисунке. Угловая скорость точки ω равна нулю в момент времени…

34.Если радиус Земли равен 6400 км, то линейная скорость точек, расположенных на экваторе Земли примерно равна…

Варианты ответа: а. 800 км/час б. 1000 км/час в. 1600 км/час г. 2000 км/час

1. Твердое тело начинает вращаться вокруг оси Z. Зависимость проекции углового ускорения на ось Z меняется от времени t согласно графику. Такому движению соответствует график зависимости проекции угловой скорости ω_z от времени…

Варианты ответа:а. 1 б.2 в.3 г.4

1. Цилиндр радиуса R катится без скольжения по горизонтальной плоскости со скоростью . График зависимости величины мгновенной скорости точки М, расположенной на вертикально прямой линии 1-О-3 ниже центра цилиндра, от расстояния r до точки О имеет вид…

Варианты ответа: а. 1 б.2 в.3 г.4

Дата добавления: 2015-07-19 ; просмотров: 871 | Нарушение авторских прав

📽️ Видео

Плоско-параллельное движение. Определение скоростей. ТермехСкачать

1 3 Кинематика вращательного движенияСкачать

Кинематика: Поступательное и вращательное движение твёрдого тела. Центр онлайн-обучения «Фоксфорд»Скачать

Физика 10 класс (Урок№5 - Поступательное движение. Вращательное движение твердого тела.)Скачать

Кинематика. Решение задач на равноускоренное движениеСкачать

Уравнение движенияСкачать