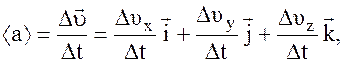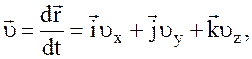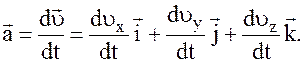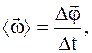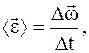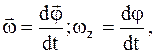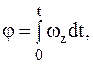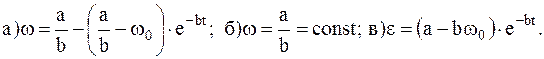Кинематические уравнения движения материальных точек имеют вид х1 а1 b1t c1t2

Кинематические уравнения движения 2-ух вещественных точек имеют вид x 1 = A1 + B1t + C1t2 и x2=A2 + B2 t + C 2 t2 , где В1=В2, C1 =-2 м/с2, C2=1 м/ с2. Обусловьте : 1) момент медли , длякоторого скорости этих точек будут равны ; 2) ускорения a1 и a2 для этого момента .

Видео:Уравнение движенияСкачать

Две материальные точки движутся согласно уравнениям: x1=A1t+B1t²+C1t³, x2=A1t+B1t²+C1t³, где A1=4 м/c, B1=8 м/с2, C1= — 16 м/с³, A2=2 м/с, B2=

Видео:Кинематика материальной точки за 20 минут (кратко и доступно) Кинематика точкиСкачать

Ваш ответ

Видео:Физика - уравнения равноускоренного движенияСкачать

решение вопроса

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Похожие вопросы

• Все категории
• экономические 43,399
• гуманитарные 33,632
• юридические 17,905
• школьный раздел 607,960
• разное 16,854

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

ОСНОВНЫЕ ФОРМУЛЫ ДЛЯ РЕШЕНИЯ ЗАДАЧ

1. Положение материальной точки в пространстве задается радиус-вектором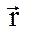

,

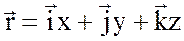
где 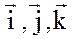– единичные векторы декартовой системы координат (орты); x, y, z – координаты точки.

Средние скорость и ускорение

Средний вектор скорости

где 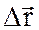– перемещение материальной точки за интервал времени Dt; – средние значения проекций скорости на координатные оси; Dx=x(t)–х₀; Dy=y(t)–y₀; Dz=z(t)–z₀ – проекции перемещения материальной точки за интервал времени Dt; x₀, y₀, z₀ – начальное положение точки в пространстве.

Среднее значение скорости:

,

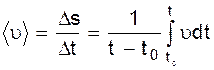
где Ds – пройденный путь за интервал времени Dt=t–t₀.

Средний вектор ускорения

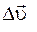
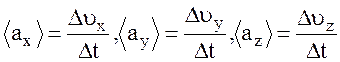
где – приращение вектора скорости материальной точки за интервал времени Dt.

– средние значения проекций ускорения на координатные оси.

Среднее ускорение ,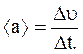

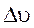
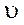
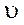
где = (t)- (t₀) .

Мгновенные скорость и ускорение

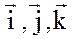
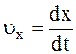
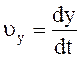
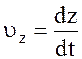
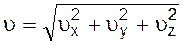
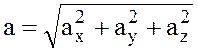
где – единичные векторы (орты осей декартовой системы координат); ; ; – проекции скорости на координатные оси.

.

.

Кинематические уравнения движения

Кинематическое уравнение движения материальной точки в векторной форме

,

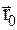
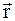
где – радиус-вектор материальной точки в начальный момент времени t₀; – радиус-вектор в произвольный момент времени t, закон изменения скорости точки со временем.

Векторное уравнение движения эквивалентно трем скалярным:

, ,

.

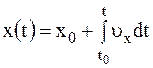
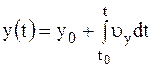
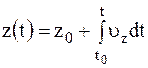
Кинематическое уравнение равномерного прямолинейного движения материальной точки вдоль оси x

Кинематическое уравнение равнопеременного прямолинейного движения (a=const) вдоль оси x

Скорость точки при равнопеременном движении вдоль оси x

Связь скорости и ускорения

Средние угловая скорость и ускорение

Средний вектор угловой скорости

где 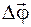– приращение угла поворота за интервал времени Dt .

Средний вектор углового ускорения

где 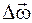– приращение угловой скорости за интервал времени Dt.

Средняя угловая скорость

, где = φ(t)- φ(t₀).

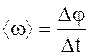
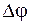
Среднее угловое ускорение

, где =ω(t)-ω(t₀).

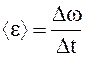
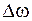
Мгновенные угловая скорость и ускорение

Мгновенная угловая скорость

где w_z – проекция угловой скорости на ось вращения.

Угловое ускорение ,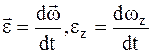

где e_z – проекция углового ускорения на ось вращения.

Угловая скорость и угловое ускорение являются аксиальными векторами, их направления совпадают с неподвижной в пространстве осью вращения.

Связь между линейными и угловыми величинами:

S=Rj; u=wR; a_t=e_zR; a_n= 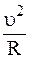=w 2 R,

где R – радиус окружности, по которой движется точка; S – длина дуги окружности; j – угол поворота, u – линейная скорость; e_z – проекция углового ускорения на ось вращения; w – угловая скорость; a_t – тангенциальное ускорение; a_n – нормальное ускорение.

При постоянной угловой скорости w=2p/T, w=2pn, где Т – период (время одного полного оборота); n – частота вращения (число оборотов, совершаемых движущейся точкой в единицу времени).

Кинематическое уравнение вращательного движения материальной точки относительно неподвижной оси

где j – угол поворота; w_z – проекция угловой скорости на ось вращения. Если w_z=const, то j=w_zt. Если угловое ускорение e=const, то 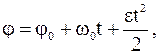где w₀ – начальная угловая скорость. Угловая скорость при таком вращении

Ускорение в плоском криволинейном движении

или
,

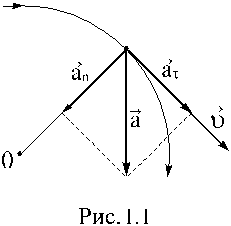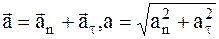
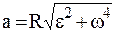
где характеризует быстроту изменения модуля скорости (см. рис. 1.1);

a_n = — характеризует быстроту изменения вектора скорости по направлению ( см. рис. 1.1).

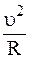
Соответствие линейных и угловых величин показано в табл.1.

Линейные величины	Угловые величины
S,х	φ
υ	ω
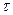а	e
an=	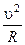an=ω 2 R
ux=u0x+axt	wz=w0z+ezt
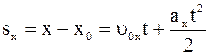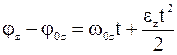2axsx=ux 2 –u0x 2	2ezjz=wz 2 –w0z 2

СПРАВОЧНЫЙ МАТЕРИАЛ

Заряд электрона e=1,6×10 -19 Кл.

Масса электрона m=9,1×10 -31 кг.

Ускорение свободного падения g=9,8 м/с 2 .

ВОПРОСЫ И УПРАЖНЕНИЯ

1. Что изучает механика как один из разделов физики?

2. Почему при изучении реальных физических явлений и объектов приходится использовать модельные представления и абстрагированные понятия? Дайте определение: а) материальной точке (частице); б) системе материальных точек; в) абсолютно твердому телу.

3. Каково содержание понятий пространства и времени в классической механике? Что означают понятия «однородность и изотропность пространства», «однородность времени»?

4. Какие существуют способы описания движения материальной точки? Что представляет собой система отсчета, система координат? Что называется радиусом-вектором ?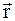

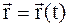
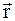
5. Покажите, что задание кинематического закона движения в координатной форме х=х (t), у=у (t), z=z (t) эквивалентно заданию его в векторной форме , где х, у, z – декартовы координаты положения материальной точки, – ее радиус-вектор. Каковы преимущества векторного описания движения?

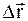
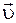
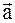
6. Дайте определение кинематических величин: а) перемещения ; б) скорости ; в) ускорения . В каких единицах измеряются эти величины? Как ориентированы векторы скорости и ускорения относительно траектории и друг друга?

7. Частица движется по закону где u₀ и g – известные постоянные; – орт координатной оси z. Найдите скорость частицы и ее ускорение , а также их проекции и как функции времени.

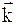
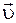
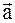
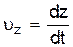
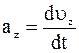
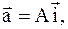
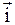
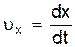
8. Ускорение движущейся частицы где A – известная постоянная; – орт координатной оси х. В момент времени t=0 х=x₀ и u_x=u₀, где х₀ и u₀ – известные постоянные (начальные условия). Найдите проекцию скорости и координату x как функции времени.

9. Какое движение абсолютно твердого тела называется: а) поступательным; б) вращательным? Приведите примеры таких движений.

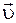
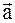
10. Что называется тангенциальным а_t и нормальным а_n ускорениями? Чему они равны? От чего зависит угол между векторами скорости и полного ускорения движущейся материальной точки?

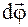
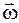
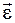
11. Какие векторы называют аксиальными? Дайте определение: а) угла поворота твердого тела; б) угловой скорости ; в) углового ускорения относительно неподвижной в пространстве оси вращения. В каких единицах измеряются эти величины?

12. Колесо вращается вокруг неподвижной оси, проходящей через его центр масс. Обладает ли любая точка на ободе тангенциальным и нормальным ускорениями, если вращение происходит: а) с постоянной угловой скоростью; б) с постоянным угловым ускорением? Изменяются ли при этом модули этих величин?

ЗАДАЧИ ГРУППЫ А

1.(1.25) Зависимость пройденного телом пути s от времени t дается уравнением s=A+Bt+Ct 2 +Dt 3 , где С=0,14 м/с 2 и D=0,01 м/с 3 . Через какое время t после начала движения тело будет иметь ускорение a=1 м/с 2 ? Найти среднее ускорение тела за этот промежуток времени.

Ответ: t=12 c, =0,64 м/с 2 .

2.(1.27) Камень, брошенный горизонтально, упал на землю через время t=0,5 с на расстоянии l=5 м по горизонтали от места бросания. С какой высоты h брошен камень? С какой скоростью u_x он брошен? С какой скоростью u он упадет на землю? Какой угол j составит вектор скорости камня с горизонтом в точке его падения на землю.

Ответ: h=1,22 м; u_x=10 м/с; u=11,1 м/с; j=26 0 12 ’ .

3.(1.30) Камень брошен горизонтально со скоростью u₀=15 м/с. Найти нормальное а_n и тангенциальное а_t ускорения камня через время t=1 с после начала движения.

Ответ: а_t=5,4 м/с 2 ; а_n=8,2 м/с 2 .

4.(1.31) Камень брошен горизонтально со скоростью u₀=10 м/с. Найти радиус кривизны R траектории камня через время t=3 с после начала движения.

Ответ: R=305 м.

5.(1.39) С башни высотой h₀=25 м брошен камень со скоростью u₀=15 м/с вверх под углом a=30 0 к горизонту. Какое время t камень будет в движении? На каком расстоянии l от основания башни он упадет на землю? С какой скоростью u он упадет на землю? Какой угол j составит траектория движения камня с горизонтом в точке его падения на землю?

Ответ: t=3,16 c; l=41,1 м; u=26,7 м/с; j=61 0 .

6.(1.49) Вентилятор вращается с частотой n=900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N=75 об. Какое время t прошло с момента выключения вентилятора до полной его остановки?

Ответ: t=10 c.

7.(1.52) Точка движется по окружности радиусом R=20 см с постоянным тангенциальным ускорением а_t. Найти тангенциальное уско-рение а_t точки, если известно, что к концу пятого оборота после начала движения линейная скорость точки u=79,2 см/с.

Ответ: а_t=0,05 м/с 2 .

8.(1.55) Колесо радиусом R=10 см вращается с угловым ускорением e 3,14 рад/с 2 . Найти для точек на ободе колеса к концу первой секунды после начала движения: а) угловую скорость w; б) линейную скорость u; в) тангенциальное ускорение а_t; г) нормальное ускорение а_n; д) полное ускорение а; е) угол a, составляемый вектором полного ускорения с радиусом колеса.

Ответ: а) w=3,14 рад/с; б) u=0,314 м/c; в) a_t=0,314 м/c 2 ;

г) a_n=0,986 м/c 2 ; д) a=1,03 м/c 2 ; е) a=17 0 46 ’ .

9.(1.57) Точка движется по окружности так, что зависимость пути от времени дается уравнением s=A–Bt+Ct 2 , где В=2 м/c и С=1 м/c 2 . Найти линейную скорость u точки, ее тангенциальное а_t, нормальное а_n и полное а ускорения через время t=3 с после начала движения, если известно, что при t¢=2 с нормальное ускорение точки а¢_n=0,5 м/c 2 .

Ответ: u=4 м/c; a_t=2 м/c 2 ; a_n=2 м/c 2 ; a=2,83 м/c 2 .

10.(1.64) Во сколько раз нормальное ускорение а_n точки,лежащей на ободе вращающегося колеса, больше ее тангенциального ускорения а_t для того момента, когда вектор полного ускорения точки составляет угол a=30 0 с вектором ее линейной скорости?

ЗАДАЧИ ГРУППЫ Б

1.(1.4) По прямой линии движутся две материальные точки согласно уравнениям: x₁=А₁+В₁t+C₁t 2 и x₂=А₂+В₂t+С₂t 2 , где А₁=5 м, В₁=1 м/с, С₁=2 м/с 2 , А₂=–6 м, В₂=4 м/с, С₂=0,8 м/с 2 . В какой момент времени t скорости этих точек будут одинаковы? Найти скорости u₁, u₂ и ускорения a₁, a₂ этих точек в момент времени t₁=1c.

Ответ: t=1,25 c; u₁=5 м/с; u₂=5,6 м/с; а₁=4 м/с 2 ; а₂=1,6 м/с 2 .

2.(1.23) Кинематические уравнения движения двух материальных точек имеют вид x₁=A₁t+B₁t 2 +C₁t 3 и x₂= A₂t+B₂t 2 +C₂t 3 ,где B₁=4 м/с 2 , С₁= -3 м/с 3 , B₂= -2 м/с 2 , С₂= 1 м/с 3 . Определить момент времени, для которого ускорение этих точек будут равны.

Ответ: t=0,5 с.

3.(1.5) Движение материальной точки задано уравнением x=Аt+Bt 2 , где А=4 м/с, В=–0,05 м/с 2 . Определить момент времени t, в который скорость точки u=0. Найти координату x и ускорение точки a в этот момент.

Ответ: t=40 c; x=80 м; а=–0,1 м/с 2 .

4.(1.6) Точка движется по окружности радиусом R=2 м. Уравнение движения точки j=Аt+Bt 3 , где А=1 с -1 , В=0,4 с -3 . Определить тангенциальноеa_t, нормальное a_n и полное a ускорения точки в момент времени t=2с.

Ответ: а_t=9,6 м/с 2 ; а_n=67,3 м/с 2 ; а=68,0 м/с 2 .

5.(1.9) Колесо радиусом R=0,2 м вращается так, что зависимость от времени линейной скорости точек, лежащих на ободе колеса, дается уравнением u=At+Bt 2 , где А=0,06 м/с 2 , В=0,02 м/с 3 . Найти угол a, который составляет вектор полного ускорения с радиусом колеса в моменты времени t₁=1 с, t₂=2с после начала движения.

Ответ: a₁=72,2 0 ; a₂=35 0 .

6. (1.34) Колесо вращается с постоянным угловым ускорением e= 3 рад/с 2 . Определить радиус колеса, если через t=1с после начала движения полное ускорение колеса a=7,5 м/с 2 .

Ответ: R=79 см.

7. На вал радиусом R=10 см намотана нить, к концу которой привязана гиря. Двигаясь равноускоренно, гиря за t=20 с от начала движения опустилась на h=2 м. Найти угловую скорость и угловое ускорение вала для этого момента времени.

Ответ: w=2h/(Rt)=2 рад/с; e=2h/(Rt 2 )=0,1 рад/с 2 .

8.(1.66) При выстреле пуля вылетела со скоростью u₀=200 м/с под углом a=60 0 к горизонту. Определить наибольшую высоту подъема h, дальность полета S и радиус кривизны R траектории пули в ее наивысшей точке. Сопротивлением воздуха пренебречь.

Ответ: h=1531 м; S=3535 м; R=1020 м.

9.(1.69) Тело брошено со скоростью u₀=20 м/с под углом a=30 0 к горизонту. Пренебрегая сопротивлением воздуха, найти скорость u тела, а также его нормальное a_n и тангенциальное a_t ускорения через t=1,5 с после начала движения. На какое расстояние x переместится за это время тело по горизонтали и на какой высоте yоно окажется?

Ответ: u=17,9 м/с; a_n=9,72 м/с 2 ; a_t=2,67 м/с 2 ; x=26 м; y=4 м.

10.(1.73) Электроны, обладающие кинетической энергией Е_к=1,6 кэВ, влетают посередине между пластинами плоского конденсатора параллельно им. Какое минимальное напряжение U_m необходимо подвести к пластинам, чтобы электроны не вышли за пределы пластин? Длина пластин l=2 см, расстояние между ними d=1 см
(1 кэВ=1,610 -16 Дж).

Ответ: U_m=800 В.

ЗАДАЧИ ГРУППЫ С

1. Скорость течения реки по ее ширине меняется по закону u=Ax 2 +Bх+C, где 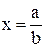(а – расстояние от берега, b – ширина реки), A=–4 м/с, B=–A, C=0,5 м/с. На какое расстояние снесет лодку течением при переправе, если скорость ее относительно стоячей воды равна u₁=2 м/с и направлена прямо к противоположному берегу? Ширина реки b=420 м.

Ответ: S=245 м.

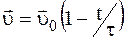
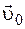
2. В момент t=0 частица вылетает из начала координат в положительном направлении оси х. Ее скорость изменяется со временем по закону , – начальная скорость, модуль которой u₀=10 см/с, t=5 с. Найти зависимость координаты частицы от времени. Рассчитать: а) координату х частицы в моменты времени 6, 10, 20 с; б) моменты времени, когда частица будет находиться на расстоянии 10 см от начала координат.

Ответ: а) x=u₀t(1–t/2t); 0,24; 0 и –4 м; б) 1,1; 9 и 11 с.

3. Радиус-вектор движущейся точки А изменяется со временем t по закону где a и b – постоянные, и – орты осей x и y. Найти: а) уравнение траектории точки; б) зависимости от времени скорости , ускорения и модули этих величин; в) зависимость от времени угла j между векторами и .

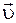
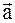
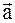
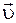
Ответ: a)

б) , a=2b;

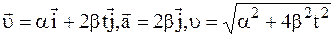
в)

4. Нормальное ускорение точки, движущейся по окружности радиусом R=4 м, изменяется по закону а_n=a+bt+ct 2 , где a, b, c – постоянные величины. Найти тангенциальное ускорение точки, путь, пройденный точкой за время t₁=6 c после начала движения, и полное
ускорение в момент времени t₂=2/3 с, если а=1 м/с 2 , b=3 м/с 3 ,
с=2,25 м/с 4 .

Ответ: а_t=3 м/с 2 , s=66 м; а=5 м/с 2 .

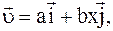
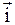
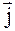
5. Частица движется в плоскости xy со скоростью где , – орты осей x и y соответственно, а и b – постоянные. В начальный момент частица находилась в точке x=y=0. Найти: a) уравнение траектории частицы y(x); б) радиус кривизны траектории в зависимости от координаты х.

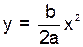
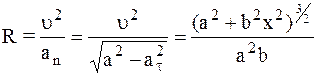
Ответ: a) ; б) .

6. Два тела бросили одновременно: одно – вертикально вверх со скоростью u₁=25 м/с, другое – под углом a=30 0 к горизонту со скоростью u₂=30 м/с. Пренебрегая сопротивлением воздуха, найти их относительную скорость во время движения.

Ответ: 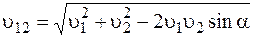=28 м/с.

7. Из пушки выпустили последовательно два снаряда со скоростью u₀=250 м/с: первый – под J₁=60 0 к горизонту, второй – под углом J₂=45 0 (азимут один и тот же). Найти интервал времени между выстрелами, при котором снаряды столкнутся друг с другом.

Ответ: 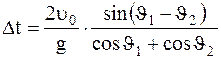=11 с.

8. Твердое тело начинает вращаться вокруг оси, неподвижной в пространстве, по закону j=аt–bt 3 , где а=6 рад/с, b=2 рад/с 3 . Найти:
а) средние значения угловой скорости и углового ускорения за промежуток времени от t=0 до остановки; б) угловое ускорение в момент остановки тела.

Ответ: a) =2а/3=4 рад/с; б) = 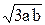=6 рад/с 2 .

9. При вращении махового колеса его угловое ускорение изменяется по закону e= — abw, а и b – постоянные. Найти: а) чему равна угловая скорость маховика через t_c после начала притормаживания, если в момент t=0 она была равна w₀? б) какой вид движения у маховика при t® ¥? в) как зависит от времени его угловое ускорение?

Ответ:

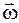
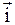
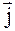
10. Твердое тело вращается с угловой скоростью =At +Bt 2 , где А=0,5 рад/с 2 , В=0,06 рад/с 3 . Найти для момента t=10 с: а) модули угловой скорости и углового ускорения; б) угол между этими векторами.

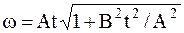
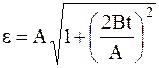
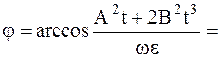
Ответ: а) =8 рад/с; =1,3 рад/с; б) 17 0 .

📸 Видео

Поступательное и вращательное движенияСкачать

К1 Определение скорости и ускорения точки по заданным уравнениям ее движенияСкачать

Кинематика точки Задание К1Скачать

Урок 15. Решение задач на графики движенияСкачать

Кинематика: Поступательное и вращательное движение твёрдого тела. Центр онлайн-обучения «Фоксфорд»Скачать

ФИЗИКА 10 класс : Механическое движение | Материальная точка, траектория, перемещение.Скачать

Поступательное и вращательное движения.Скачать

Кинематика точки. Три способа задания движения. Скорость, ускорениеСкачать

Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Уравнение равномерного движения. Решение задач по теме.Скачать

Поступательное движение. Материальная точкаСкачать

кинематика точкиСкачать

Кинематика вращательного движения. ТермехСкачать

ФИЗИКА ЕГЭ 2021. Кинематика. Графики движения. Часть 1.Скачать

Криволинейное, равномерное движение материальной точки по окружности. Практическая часть. 9 класс.Скачать