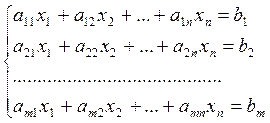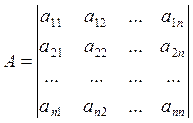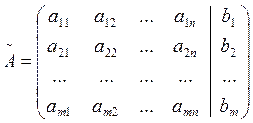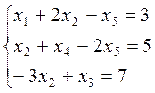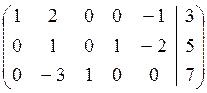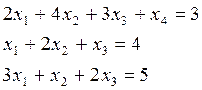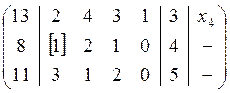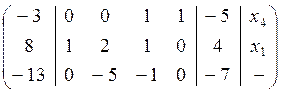Каждое уравнение переменные входят как сумма произведений переменных в разных сочетаниях (3 видео)

Системы линейных уравнений. Основные понятия. Переменные, входящие в уравнения системы

Содержание

Страницы работы
Содержание работы
Как решать многочлены от нескольких переменных — пояснения
Понятие многочлена от нескольких переменных
Виды многочленов
Многочлены от двух переменных
Многочлены от нескольких переменных
Сумма многочленов
Разность многочленов
Произведение многочлена и одночлена
Произведение двух многочленов
Каноническая форма многочлена
Примеры решения задач для самостоятельного разбора новой темы
Каждое уравнение переменные входят как сумма произведений переменных в разных сочетаниях
💥 Видео

Страницы работы

Содержание работы

Глава 7 Системы линейных уравнений.

Определение 1:Системой линейных уравнений называется система вида:

Определение 2: Решением системы линейных уравнений называется упорядоченный набор чисел 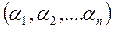при подстановке которых в исходную систему каждое из уравнений обращается в тождество.

Определение 3: Основной матрицей системы линейных уравнений называется матрица А размерности 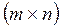, образованная из коэффициентов при неизвестных:

Определение 4: Основная матрица А системы дополненная столбцом свободных членов, называется расширенной матрицей системы и обозначается .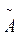

Определение 5: Система уравнений называется совместной, если она имеет хотя бы одно решение и несовместной если у неё нет.

Определение 6: Система уравнений называется однородной, если все свободные члены равны нулю.

Определение 7: Неизвестная х_i в системе линейных уравнений называется базисной, если она встречается в единственном уравнении системы и имеет коэффициент равный единице.

Определение 8: Система уравнений имеет базисный вид, то есть приведена к единичному базису, если в каждом уравнении выделена одна базисная переменная.

Приведём системы базисного вида:

Расширенная матрица этой системы:

Нетрудно увидеть, что базисными переменными в приведённом примере являются переменные х₁, х₃, х₄.

Определение 9: Переменные входящие в уравнения системы и не являющиеся базисными называются свободными переменными.

Определение 10: Две системы линейных уравнений называются равносильными, если множества их решений совпадают. Все несовместные системы равносильны.

Перечислим элементарные преобразования систем, приводящие к равносильным системам:

2. Умножение на число 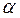правой и левой части любого уравнения.

3. Прибавление к левой и правой части i-ого уравнения соответствующих частей j – ого уравнения, умноженных на число .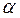

4. Перестановка местами i-ого и j-ого уравнений.

7.2 Решение системы линейных уравнений методом Жордана-Гаусса.

Этот метод позволяет привести к базисному виду совместную систему уравнений.

Элементарные преобразования будем осуществлять по следующей схеме.

1. Выбираем разрешающий элемент в каком либо уравнении и если этот элемент расширенной матрицы не является единицей, то элементы разрешающей строки делим на этот элемент.

2. Разрешающий столбец с помощью элементарных преобразований заполняем нулями.

3. Получаем новую расширенную матрицу, в которой снова выбираем другую разрешающую строку и повторяем все действия.

4. В случае возникновения нулевой строки ее вычеркиваем.

5. В случае возникновения строки вида: 0х₁+0х₂+0х_n=b_i система не имеет решений, то есть является несовместной.

Рассмотрим пример решения системы с использованием столбца контрольных сумм КΣ, которые представляют собой суммы всех коэффициентов, соответствующих уравнений. Эти числа преобразуются по тем же правилам, что и остальные элементы матрицы. Контроль состоит в том, что на каждом этапе проверяется совпадение контрольной суммы с суммой всех коэффициентов данного уравнения. Решим систему уравнений.

Составим расширенную матрицу системы, причем в первом столбце будут контрольные суммы, а в последнем будем указывать базисные переменные. Легко видеть что в первом уравнении такой переменной будет переменная х₄.

выберем разрешающий элемент во второй строке, пусть это будет 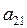. Используя элементарные преобразования, получим матрицу у которой все остальные элементы разрешающего столбца были нулевые, для этого выполняются следующие элементарные преобразования:

1. Разрешающая строка умножается на (-2) и складывается с первой строкой, результат записываем на место первой строки.

2. Разрешающая строка умножается на (-3) и складывается с третьей строкой, результат записывается на место третьей строки.

В результате получаем матрицу:

Используя столбец контрольных сумм, сделаем проверку:

Следующим шагом необходимо выбрать разрешающий элемент в третьей строке. В качестве такого элемента можно взять элемент 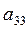, но для того чтобы этот элемент стал равным единице, умножим элементы третьей строки на (-1). Получим матрицу вида:

используя элементарные преобразования, преобразуем разрешающий столбец матрицы так, чтобы все элементы кроме разрешающего (базисного) стали равны нулю, для этого выполняем следующие элементарные преобразования.

1. Разрешающая строка умножается на (-1) и складывается со второй строкой, результат записывается на место второй строки.

2. Разрешающая строка умножается на (-1) и суммируется с первой строкой, результат записывается на место первой строки.

Видео:Уравнение с двумя переменными и его график. Алгебра, 9 классСкачать

Как решать многочлены от нескольких переменных — пояснения

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Понятие многочлена от нескольких переменных

Одночлен — тип числа, переменные, их произведения и степени.

Многочлен — сумма различных одночленов. Примером многочлена может считаться уравнение 31 x y 5 + y 6 + 3 x z 5 .

Члены многочлена — абсолютно все одночлены, которые входят в состав многочлена.

Многочлен стандартного вида — тип многочлена, который состоит из одночленов стандартного вида, не имеющих соответствующих членов.

Степень многочлена стандартного вида — самая большая степень из перечня степеней одночленов, которые входят в его состав.

Для термина «многочлен нескольких переменных» возможно выделить несколько частных вариантов: трехчлен и двучлен.

Двучлен — такой многочлен, который состоит из двух членов. Примером двучлена служит следующее уравнение: 6 b 6 + 13 a c 5 .

Трехчлен — такой многочлен, который состоит из трех членов. Примером трехчлена служит следующее уравнение: x y 5 + y 6 + x z 5 .

При помощи многочлена вводят такие термины как «алгебраическое уравнение», «алгебраическое число», а также алгебраическая функция».

Виды многочленов

Существуют следующие виды многочленов:

унитарным, приведенным, нормированным называют многочлен с одной переменной, если старший коэффициент равняется единице;
однородным называют многочлен, при котором все одночлены обладают одной и той же полной степенью. Пример: x 2 + x y + y 2 является однородным многочленом с двумя переменными, а x 2 + y + 1 не будет считаться однородным;
приводимым называется многочлен, который возможно разложить в виде произведения многочленов низших степеней с коэффициентами из определенного поля, а ином случае такой многочлен является неприводимым.

Многочлены от двух переменных

Для обозначения переменных возьмем две латинские буквы — y и x, которые обычно используются в алгебре. Представим произведение a × x k × y l , где a будет являться числом, которое можно назвать одночленом. Степень данного числа будет равна k+l. Сумма одночленов считается многочленом.

В отличие от многочленов с одной переменной, для многочленов, у которых большое количество переменных, не существует общепринятой шаблонной записи.

Как и многочлены с одной переменной, многочлены с несколькими переменными имеют способность к разложению на множители. Самым главным разложением является разложение разности n-ых степеней, которое более известно всем в использовании для n=2 и n=3.

x 2 — y 2 = ( x — y ) ( x + y )

x 3 — y 3 = ( x — y ) ( x 2 + x × y + y 2 )

Данные формулы можно обобщить для произвольного n:

x n — y n = ( x — y ) ( x n — 1 + x n — 2 × y + . . . + x × y n — 2 + y n — 1 )

Сумму n — ы х степеней возможно с легкостью разложить в тех случаях, когда n является нечетным. Слагаемое y n возможно представить в форме — ( — y ) n , а также применить формулу разложения разности n — ы х степеней.

x 5 + y 5 = x 5 — ( — y ) 5 = ( x — ( — y ) ) × ( x 4 + x 3 × ( — y ) + x 2 × ( — y ) 2 + x × ( — y ) 3 + ( — y ) 4 ) = ( x + y ) × ( x 4 — x 3 × y + x 2 × y 3 + y 4 ) .

Данное тождество может быть проверено прямым перемножением скобок правой части.

Многочлены от нескольких переменных

Как и в случае с двумя переменными возможно построить многочлены от любого количества переменных. Возьмем m количество букв x 1 , x 2 , … Совершим построение одночленов x k 1 , x l 2 , . . . , x z n . Многочленом называется сумма данных одночленов, которые снабжены числовыми коэффициентами.

Покажем ряд тождеств, в которых могут использоваться многочлены с несколькими переменными.

1 ) x 3 + y 3 + z 3 — 3 × x y z = ( x + y + z ) × ( x 2 + y 2 + z 2 — x y — y z — x z ,

2 ) ( a 2 + b 2 + c 2 ) × ( x 2 + y 2 + z 2 ) = ( z x + b y + c z ) 2 + ( a y — b x ) 2 + ( a z — c x ) 2 + ( b z — c y ) 2 ,

3 ) ( x — x 1 ) × ( x — x 2 ) × ( x — x 3 ) = x 3 — ( x 1 + x 2 + x 3 ) × x 2 + ( x 1 x 2 + x 2 x 3 + x 3 x 1 ) × x — x 1 x 2 x 3 .

Степень одночлена — такая сумма степеней, с которыми в данный одночлен входят все буквы. Степень многочлена — самая большая степень одночлена, входящего в многочлен (с условием ненулевого коэффициента). Рассмотрим примеры, которые приведены выше.

В первом примере в левой части находится многочлен третьей степени с разными переменными (обозначается буквами x, z, y).

Во втором примере многочлен находится в четвертой степени с переменными, которые обозначаются буквами a, b, c, x, y, z.

В третьем случае многочлен находится в третьей степени с четырьмя буквами x, x1, x2, x3.

Многочлен считается однородным в том случае, если все его одночлены обладают одним и тем же коэффициентом степени. В примерах выше все многочлены считаются однородными. Среди многочленов с несколькими буквами выделяют симметричные многочлены. В примерах выше первые два примера считаются симметричными. Можно особо отметить базовые симметричные многочлены, как и в варианте с двумя переменными.

F 0 = 1 , F 1 = x 1 + . . . + x m , F 2 = x 1 x 2 + . . . + x m — 1 x m , F m = x 1 x 2 × . . . × x m .

В данных формулах F n является суммой всех возможных произведений, которые взяты по k букв из информации m букв. Как и в случае с двумя буквами, каждый симметричный многочлен будет представлен в качестве многочлена от базовых симметричных многочленов.

Бином Ньютона является одним из самых известных многочленов от двух переменных. Бином представляет собой разложение степени двучлена ( a x + b y ) n в сумму одночленов.

Рассмотрим, какие действия можно совершать с многочленами.

Сумма многочленов

У многочленов существует способность складываться друг с другом. Приведем пару простых примеров.

Совершим сложение следующих уравнений:

3 x y 5 + 6 y 6 + 13 x 5 , а также 6 y 6 — x y 5 + 3 x 5 .

Первый этап сложения — записать данные многочлены в виде суммы:

( 3 x y 5 + 6 y 6 + 13 x 5 ) + ( 6 y 6 — x y 5 + 3 x 5 ) .

Далее нужно раскрыть скобки в данном уравнении:

3 x y 5 + 6 y 6 + 13 x 5 + 6 y 6 — x y 5 + 3 x 5 .

Далее нужно привести подобные слагаемые. В итоге получим следующее уравнение:

2 x y 5 + 12 y 6 + 16 x 5 .

Получается, что результат суммы данных двух многочленов дает такой же многочлен.

Разность многочленов

Также над данными типами чисел можно совершать действие вычитания. Рассмотрим небольшой пример данного действия.

Совершаем вычитание следующих уравнений:

3 x y 5 + 6 y 6 + 13 x 5 и 6 y 6 — x y 5 + 3 x 5 .

Первый шаг в решении такого типа заданий — записать данное уравнение в качестве разности:

( 3 x y 5 + 6 y 6 + 13 x 5 ) — ( 6 y 6 — x y 5 + 3 x 5 ) .

Далее раскрываем скобки: 3 x y 5 + 6 y 6 + 13 x 5 — 6 y 6 + x y 5 — 3 x 5 .

Стоит помнить, что если перед скобками находится знак минус, то в случае раскрытия скобок знаки поменяются на противоположные. Приводим подобные слагаемые, в итоге получаются:

4 x y 5 + 10 x 5 .

Получается, что в результате разности получается такой же многочлен.

Произведение многочлена и одночлена

В итоге умножения всегда получается только многочлен. Рассмотрим этапы умножения:

составляют определенное произведение;
раскрывают скобки;
для раскрытия скобок в процессе умножения нужно сделать умножение каждого одночлена на каждый элемент многочлена, а также нужно сложить данные уравнения между собой;
происходит группировка одних чисел с другими, одинаковых переменных друг с другом;
происходит умножение чисел, а также складываются степени соответствующих одинаковых переменных.

Совершим умножение одночлена ( — m 2 n ) на многочлен ( m 2 n 2 — m 2 — n 2 ) .

Решение. Составляется произведение:

( — m 2 n ) × ( m 2 n 2 — m 2 — n 2 ) .

( — m 2 n ) × m 2 n 2 + ( — m 2 n ) × ( — m 2 ) + ( — m 2 n ) × ( — n 2 ) .

После умножения получится следующее выражение: — m 4 n 3 + m 4 n + m 2 n 3 .

Произведение двух многочленов

Представим правило умножения: нужно каждый элемент первого многочлена перемножить на каждый элемент второго многочлена, далее нужно произвести сложение полученных результатов, итоговый многочлен нужно привести к стандартному виду.

Произведением умножение многочлена на многочлен ( 1 — 4 x 2 ) и ( 5 y 2 — 3 x — 2 ) .

Нужно составить соответствующее произведение: ( 1 — 4 x 2 ) × ( 5 y 2 — 3 x — 2 ) .

Раскрываются скобки согласно правилу: 5 y 2 — 3 x — 2 — 20 x 2 y 2 + 12 x 3 + 8 x 2 .

Данный многочлен обладает стандартным видом, а, значит, ответом будет:

5 y 2 — 3 x — 2 — 20 x 2 y 2 + 12 x 3 + 8 x 2 .

Также возможно совершить деление, при котором можно перейти полностью к сокращению дроби (то есть перейти на уровень, когда дробь под чертой можно сократить).

Видео:Как решать неравенства? Часть 1| МатематикаСкачать

Каноническая форма многочлена

Стандартный многочлен степени m (полином) от одинарной переменной x — уравнение формы типа

a ( x ) = a 0 + a 1 x + a 2 x 2 + . . . + a m x m = ∑ i = 0 m a i x i ,

при котором a i ∈ K , a m ≠ 0 .

Часть a i является коэффициентами многочлена. Они могут являться нулевыми (как элементы, так и все полностью).

Можно определить каноническую форму многочлена таким образом: находится самое большое i.

Оно должно быть таким, чтобы a i ≠ 0 , допустим, i = n .

Получается следующее выражение: a ( x ) = a 0 + a 1 x 1 + a 2 x 2 + . . . a n x n , a n ≠ 0 .

Если абсолютно все a i стремятся к нулю, то каноническая форма будет нулем.

Число 0 ∈ K будет читаться многочленом с нулевыми коэффициентами, носит название нулевых многочленов. Однако степень нулевого многочлена является неопределенной.

Видео:Решение уравнения методом замены переменнойСкачать

Примеры решения задач для самостоятельного разбора новой темы

Представим задачу на многочлены от нескольких переменных

Умножить многочлены ( a 2 + b + 1 ) и ( a 2 — 24 b + 6 ) . Привести результат к стандартному виду.

Решение. Нужно составить выражение ( a 2 + b + 1 ) × ( a 2 — 24 b + 6 ) .

Раскрываем скобки согласно правилу: a 4 — 24 a 2 b + 6 a 2 + a 2 b — 24 b 2 + 6 b + a 2 — 24 b + 6 .

Приводим его к стандартному виду: a 4 — 23 a 2 b + 7 a 2 — 24 b 2 — 18 b + 6 .

Ответ: a 4 — 23 a 2 b + 7 a 2 — 24 b 2 — 18 b + 6 .

Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Каждое уравнение переменные входят как сумма произведений переменных в разных сочетаниях

Два уравнения называют равносильными, если они имеют одно и тоже множество корней.

Свойства уравнений

Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, равносильное данному.
Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, равносильное данному.
Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, равносильное данному

Линейное уравнение

Уравнение вида , где — переменная, и некоторые числа, называют линейным уравнением с одной переменной.

Значения и
Корни уравнения		-любое число	корней нет

Одночлены и многочлены

Одночлены

Выражения, являющиеся произведениями чисел, переменных и их степеней, называют одночленами.
Одночлен, содержащий только один отличный от нуля числовой множитель, стоящий на первом месте, а все остальные множители которого — степени с разными основаниями, называют одночленом стандартного вида. К одночленам стандартного вида также относят числа, отличные от нуля, переменные и их степени.
Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена.
Одночлены, имеющие одинаковые буквенные части, называют подобными. Степенью одночлена называют сумму показателей степеней всех переменных, входящих в него. Степень одночлена, являющегося числом, отличным от нуля, считают равной нулю.
Нуль-одночлен степени не имеет.

Многочлены

Выражение, являющееся суммой нескольких одночленов, называют многочленом.
Одночлены, из которых состоит многочлен, называют членами многочлена.
Одночлен является частным случаем многочлена. Считают, что такой многочлен состоит из одного члена.

Умножение одночлена на многочлен

Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый член многочлена и полученные произведения сложить.

Умножение многочлена на многочлен

Чтобы умножить многочлен на многочлен, можно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.

Формулы сокращенного умножения

Разность квадратов двух выражений

Разность квадратов двух выражений равна произведению разности этих выражений и их суммы:

Произведение разности и суммы двух выражений

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений:

Квадрат суммы и квадрат разности двух выражений

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения:

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений пл юс квадрат второго выражении:

Преобразование многочлена в квадрат суммы или разности двух выражений

позволяют «свернуть» трёхчлен в квадрат двучлена.

Трёхчлен, который можно представить в виде квадрата двучлена, н а зывают полным квадратом.

Сумма и разность кубов двух выражений

Многочлен называют неполным квадратом разности.

Сумма кубов двух выражений равна произведению суммы этих выр а жений и неполного квадрата их разности:

Многочлен называют неполным квадратом суммы.

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы:

Степень. Свойства степени с целым показателем

Свойства степени с целым показателем

Для любого и любых целых выполняются равенства:

Для любых , и любого целого выполняются равенства:

Функция. Область определения и область значений функции

Функция

Правило, с помощью которого по каждому значению независимой переменной можно найти единственное значение зависимой переменной, называют функцией, а соответствующую зависимость одной п e ременной от другой — функциональной.
Обычно независимую переменную обозначают , зависимую обозначают , функцию(правило) — .
Независимую переменную называют аргументом функции. Значение зависимой переменной называют значением функции.
Тогда функциональную зависимость обозначают .
Значения, которые принимает аргумент, образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.

Способы задания функции

Описательный, табличный, с помощью формулы, графический.

График функции

Графиком функции называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.

Линейная функция, её график и свойства

Функцию, которую можно задать формулой вида , где и — некоторые числа, — независимая переменная, называют линейной.
Графиком линейной функции является прямая.
Линейную функцию, заданную формулой , где , называют прямой пропорциональностью.

Системы линейных уравнений с двумя переменными

Уравнение с двумя переменными

Пару значений переменных, обращающую уравнение с двумя переменными в верное равенство, называют решением уравнения с двумя переменными.

Решить уравнение с двумя переменными — значит найти все его решения или показать, что оно не имеет решений.

Графиком уравнения с двумя переменными называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, координаты которых (пары чисел) являются решениями данного уравнения.

Если некоторая фигура является графиком уравнения, то выполняются два условия:

все решения уравнения являются координатами точек, принадлежащих графику;
координаты любой точки, принадлежащей графику, — это пара чисел, являющаяся решением данного уравнения.

Графический метод решения системы двух линейных уравнений с двумя переменными

Графический метод решения системы уравнений заключается в следующем:

построить в одной координатной плоскости графики уравнений, входящих в систему;
найти координаты всех точек пересечения построенных графиков;
полученные пары чисел и будут искомыми решениями.

Если графиками уравнений, входящих в систему линейных уравнении, являются прямые, то количество решений этой системы зависит от взаимного расположения двух прямых на плоскости:

если прямые пересекаются, то система имеет единственное решение.
если прямые совпадают, то система имеет бесконечно много решении.
если прямые параллельны, то система решений не имеет.

Решение системы двух линейных уравнений с двумя переменными методом подстановки

Чтобы решить систему линейных уравнений методом подстановки, следует:

выразить из любого уравнения системы одну переменную через другую;
подставить в уравнение системы вместо этой переменной выражение, полученное на первом шаге;
решить уравнение с одной переменной, полученное на втором шаге;
подставить найденное значение переменной в выражение, полученное на первом шаге;
вычислить значение второй переменной;
записать ответ.

Решение систем линейных уравнений методом сложения

Чтобы решить систему линейных уравнений методом сложения, следует:

подобрать такие множители для уравнений, чтобы после преобразований коэффициенты при одной из переменной стали противоположными числами
сложить почленно левые и правые части уравнений, полученных на первом шаге
решить уравнение с одной переменной, полученной на втором шаге
подставить найденное на третьем шаге значение переменной в любое из уравнений исходной системы;
вычислить значение второй переменной;
записать ответ.