- Карточки для коррекции знаний
- Скачать:
- Предварительный просмотр:
- Предварительный просмотр:
- Предварительный просмотр:
- Предварительный просмотр:
- Карточки к уроку «Решение квадратных уравнений»
- Решение квадратных уравнений по формуле
- Просмотр содержимого документа «Решение квадратных уравнений по формуле»
- 📺 Видео
Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать
Карточки для коррекции знаний
Коррекция знаний бывает крайне необходима. И правильно составленные задания по темам помогут наладить эту работу.
Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать
Скачать:
| Вложение | Размер |
|---|---|
| kvadrat_summy.doc | 32 КБ |
| raznost_kvadratov.doc | 32 КБ |
| nepolnye_kvadratnye_uravneniya.doc | 43 КБ |
| kvadratnye_uravneniya.doc | 35.5 КБ |
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать
Предварительный просмотр:
А – 7 Карточка № 4. Формула квадрата суммы.
(I + II) 2 = I 2 + 2 ∙ I ∙ II + II 2 .
2 ∙ I ∙ II = 2 ∙ 3х ∙ 4,
(3х+ 4) 2 =(3х) 2 +2 ∙3х∙4+4 2 =
Преобразовать выражение по данной формуле, если это возможно:
- (а + в) 2 ;
- х 2 + 2ху + у 2 ;
- т 2 + 3тп + п 2 ;
- (2п + 3) 2 ;
- а 2 – 4а + 4.
- (х – у) 2 ;
- а 2 + 2ав + в 2 ;
- р 2 + 4рк + к 2 ;
- (2 + 3х) 2 ;
- а 2 + 6а + 9.
25х 2 + 10ху + у 2 = ?
I 2 = 25х 2 =(5х) 2 , I = 5х,
II 2 = у 2 , II = у,
2 ∙ I ∙ II = 10ху = 2 ∙ 5х ∙ у,
25х 2 + 10ху + у 2 =(5х + у) 2 .
- (с + в) 2 ;
- 1 + 2х + х 2 ;
- а 2 + 8а + 16;
- (2р + п) 2 ;
- 4а 2 – 4а + 1.
Видео:Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать
Предварительный просмотр:
А – 7 Карточка № 6. Формула разности квадратов.
(I – II)( I + II) = I 2 – II 2 .
I 2 = 4х 2 , II 2 = 9у 2 ;
(2х + 3у)(2х – 3у)=4х 2 – 9у 2 .
Преобразовать выражение по данной формуле, если это возможно:
- (х – у)(х + у)
- а 2 – с 2 ;
- (а – 10)(10 + а);
- р 2 + п 2 ;
- 25т 2 – 16п 2 .
- (а – в)(а + в);
- 4а 2 — 1;
- (3а + 2)(3а – 2);
- х 2 + 4;
- 9а 2 — 4 9.
а 2 – 25 = (а – 5)(а + 5).
- (а – с)(а + с);
- 100 — х 2 ;
- (3 + п)(п – 3);
- 1 + х 2 ;
Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать
Предварительный просмотр:
А – 8 Карточка № 9. Решение неполных квадратных уравнений.
Уравнение вида ах 2 = 0 решается так:
ах 2 = 0, х 2 = 0 (так как а≠0 ), х =0.
Уравнение вида ах 2 + вх = 0 решается так:
ах 2 + вх = 0, х ( ах + а) = 0,
х = 0 или ах + в = 0,
Уравнение вида ах 2 + с = 0 решается так:
ах 2 + с = 0, ах 2 = — с, так как а≠0;
а) 2х 2 + 8 = 0, б) 3х 2 – 2х = 0,
в) 7х 2 – 8 = 0, г) 6х 2 = 0.
а) 2х 2 + 8 = 0 – уравнение вида ах 2 + с = 0;
2х 2 + 8 = 0, 2х 2 = — 8, х 2 = — 4.
Ответ: корней нет.
б) 3х 2 – 2х = 0 – уравнение вида ах 2 + вх = 0 ;
3х 2 – 2х = 0, х (3х – 2) = 0, х = 0 или 3х – 2 = 0 значит х = 0 или Ответ:
в) 7х 2 – 8 = 0 – уравнение вида ах 2 + с = 0 ;
7х 2 – 8 = 0 , 7х 2 = 8, х 2 = ,
г) 6х 2 = 0 – уравнение вида ах 2 = 0;
6х 2 = 0, х 2 = 0, х = 0.
- 3х 2 + 1 = 0;
- – х 2 + 5х = 0;
- 7х 2 – 14 = 0;
- – х 2 = 0;
- 4(х – 1) 2 – 16 = 0;
- 5х 2 – 5 = 0;
- 3 х 2 + 6х = 0;
- 2х 2 + 8 = 0;
- 4 х 2 = 0;
10)5(х – 12) 2 – 45 = 0;
15)3(х + 1) 2 – 27 = 0;
Видео:ТЕОРЕМА ВИЕТА ЗА 2 МИНУТЫСкачать
Предварительный просмотр:
А – 8 Карточка № 10. Решение квадратных уравнений по формуле.
Чтобы решить по формуле квадратное уравнение
Видео:Решение биквадратных уравнений. 8 класс.Скачать
Карточки к уроку «Решение квадратных уравнений»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
1. Уравнение вида 
, где a, b, c — заданные числа, a
0, x — переменная, называется.
2. Полное квадратное уравнение не имеет корней, если D .
3. Уравнение вида 
называется.
4. Квадратное уравнение имеет два корня, если
.
5. Сумма корней приведенного квадратного уравнения равна …
6. Дано уравнение
. D =.
1. Если квадратное уравнение, то a . коэффициент, с.
2. Уравнение x² = a, где a
3. Полное квадратное уравнение имеет единственный корень, если .
4. Уравнение вида ax² + c = 0, где a 0, c 0, называют . квадратным уравнением.
5. Произведение корней приведенного квадратного уравнения равно …
6. Дано уравнение x²- 6x + 8 = 0. D =.
1. Уравнение вида , где a, b, c — заданные числа, a0, x — переменная, называется.
2. Полное квадратное уравнение не имеет корней, если D .
3. Уравнение вида называется.
4. Квадратное уравнение имеет два корня, если.
5. Сумма корней приведенного квадратного уравнения равна …
6. Дано уравнение. D =.
1. Если квадратное уравнение, то a . коэффициент, с.
2. Уравнение x² = a, где a
3. Полное квадратное уравнение имеет единственный корень, если .
4. Уравнение вида ax² + c = 0, где a 0, c 0, называют . квадратным уравнением.
5. Произведение корней приведенного квадратного уравнения равно …
6. Дано уравнение x²- 6x + 8 = 0. D =.
1. Уравнение вида , где a, b, c — заданные числа, a0, x — переменная, называется.
2. Полное квадратное уравнение не имеет корней, если D .
3. Уравнение вида называется.
4. Квадратное уравнение имеет два корня, если.
5. Сумма корней приведенного квадратного уравнения равна …
6. Дано уравнение. D =.
1. Если квадратное уравнение, то a . коэффициент, с.
2. Уравнение x² = a, где a
3. Полное квадратное уравнение имеет единственный корень, если .
4. Уравнение вида ax² + c = 0, где a 0, c 0, называют . квадратным уравнением.
5. Произведение корней приведенного квадратного уравнения равно …
6. Дано уравнение x²- 6x + 8 = 0. D =.
1. Уравнение вида , где a, b, c — заданные числа, a0, x — переменная, называется.
2. Полное квадратное уравнение не имеет корней, если D .
3. Уравнение вида называется.
4. Квадратное уравнение имеет два корня, если.
5. Сумма корней приведенного квадратного уравнения равна …
6. Дано уравнение. D =.
1. Если квадратное уравнение, то a . коэффициент, с.
2. Уравнение x² = a, где a
3. Полное квадратное уравнение имеет единственный корень, если .
4. Уравнение вида ax² + c = 0, где a 0, c 0, называют . квадратным уравнением.
5. Произведение корней приведенного квадратного уравнения равно …
6. Дано уравнение x²- 6x + 8 = 0. D =.
1. Уравнение вида , где a, b, c — заданные числа, a0, x — переменная, называется.
2. Полное квадратное уравнение не имеет корней, если D .
3. Уравнение вида называется.
4. Квадратное уравнение имеет два корня, если.
5. Сумма корней приведенного квадратного уравнения равна …
6. Дано уравнение. D =.
1. Если квадратное уравнение, то a . коэффициент, с.
2. Уравнение x² = a, где a
3. Полное квадратное уравнение имеет единственный корень, если .
4. Уравнение вида ax² + c = 0, где a 0, c 0, называют . квадратным уравнением.
5. Произведение корней приведенного квадратного уравнения равно …
6. Дано уравнение x²- 6x + 8 = 0. D =.
1. Уравнение вида , где a, b, c — заданные числа, a0, x — переменная, называется.
2. Полное квадратное уравнение не имеет корней, если D .
3. Уравнение вида называется.
4. Квадратное уравнение имеет два корня, если.
5. Сумма корней приведенного квадратного уравнения равна …
6. Дано уравнение. D =.
1. Если квадратное уравнение, то a . коэффициент, с.
2. Уравнение x² = a, где a
3. Полное квадратное уравнение имеет единственный корень, если .
4. Уравнение вида ax² + c = 0, где a 0, c 0, называют . квадратным уравнением.
5. Произведение корней приведенного квадратного уравнения равно …
6. Дано уравнение x²- 6x + 8 = 0. D =.
1. Уравнение вида , где a, b, c — заданные числа, a0, x — переменная, называется.
2. Полное квадратное уравнение не имеет корней, если D .
3. Уравнение вида называется.
4. Квадратное уравнение имеет два корня, если.
5. Сумма корней приведенного квадратного уравнения равна …
6. Дано уравнение. D =.
1. Если квадратное уравнение, то a . коэффициент, с.
2. Уравнение x² = a, где a
3. Полное квадратное уравнение имеет единственный корень, если .
4. Уравнение вида ax² + c = 0, где a 0, c 0, называют . квадратным уравнением.
5. Произведение корней приведенного квадратного уравнения равно …
6. Дано уравнение x²- 6x + 8 = 0. D =.
1. Уравнение вида , где a, b, c — заданные числа, a0, x — переменная, называется.
2. Полное квадратное уравнение не имеет корней, если D .
3. Уравнение вида называется.
4. Квадратное уравнение имеет два корня, если.
5. Сумма корней приведенного квадратного уравнения равна …
6. Дано уравнение. D =.
1. Если квадратное уравнение, то a . коэффициент, с.
2. Уравнение x² = a, где a
3. Полное квадратное уравнение имеет единственный корень, если .
4. Уравнение вида ax² + c = 0, где a 0, c 0, называют . квадратным уравнением.
5. Произведение корней приведенного квадратного уравнения равно …
6. Дано уравнение x²- 6x + 8 = 0. D =.
1. Уравнение вида , где a, b, c — заданные числа, a0, x — переменная, называется.
2. Полное квадратное уравнение не имеет корней, если D .
3. Уравнение вида называется.
4. Квадратное уравнение имеет два корня, если.
5. Сумма корней приведенного квадратного уравнения равна …
6. Дано уравнение. D =.
1. Если квадратное уравнение, то a . коэффициент, с.
2. Уравнение x² = a, где a
3. Полное квадратное уравнение имеет единственный корень, если .
4. Уравнение вида ax² + c = 0, где a 0, c 0, называют . квадратным уравнением.
5. Произведение корней приведенного квадратного уравнения равно …
6. Дано уравнение x²- 6x + 8 = 0. D =.
Реши уравнение, выделением квадрата двучлена: х 2 -6х+9=0
Реши уравнение: 2х 2 -9х+10=0
Составь квадратное уравнение, если его корни 5 и -2.
5х 2 =9( 
) 2 +2
х 2 -4( ) 2 -12=0
1. Одно из двух натуральных чисел больше другого на 5. Найдите эти числа, если их произведение равно 24.
2. Площадь прямоугольной пластины равна 120 см 2 . Найдите длину и ширину пластины, если известно, что длина на 2см больше ширины.
3. В прямоугольном треугольнике один из катетов на 7 см больше другого. Найдите периметр, если гипотенуза равна 13см.
1. Одно из двух натуральных чисел больше другого на 5. Найдите эти числа, если их произведение равно 24.
2. Площадь прямоугольной пластины равна 120 см 2 . Найдите длину и ширину пластины, если известно, что длина на 2см больше ширины.
3. В прямоугольном треугольнике один из катетов на 7 см больше другого. Найдите периметр, если гипотенуза равна 13см.
1. Одно из двух натуральных чисел больше другого на 5. Найдите эти числа, если их произведение равно 24.
2. Площадь прямоугольной пластины равна 120 см 2 . Найдите длину и ширину пластины, если известно, что длина на 2см больше ширины.
3. В прямоугольном треугольнике один из катетов на 7 см больше другого. Найдите периметр, если гипотенуза равна 13см.
1. Одно из двух натуральных чисел больше другого на 5. Найдите эти числа, если их произведение равно 24.
2. Площадь прямоугольной пластины равна 120 см 2 . Найдите длину и ширину пластины, если известно, что длина на 2см больше ширины.
3. В прямоугольном треугольнике один из катетов на 7 см больше другого. Найдите периметр, если гипотенуза равна 13см.
Видео:Быстрый способ решения квадратного уравненияСкачать
Решение квадратных уравнений по формуле
Данный тест составлен в соответствии с УМК Макарычева «Алгебра 7-9 кл». Тест содержит два варианта, ответы.
Просмотр содержимого документа
«Решение квадратных уравнений по формуле»
Тест «Решение квадратных уравнений по формуле»
Инструкция: В заданиях с 1 по 9 выберите только один правильный ответ из предложенных.
В задании 10 запишите решение и ответ.
1. Какое из квадратных уравнений является полным:
А) 5х 2 = 0 Б) 8 — 2х + 3х 2 = 0 В) 7х 2 + 1 = 0 Г) 6х — х 2 = 0
2. Дискриминант квадратного уравнения х 2 + 5х – 6 = 0 равен:
А) 0 Б) 49 В) 1 Г) 16
3. Сколько корней имеет квадратное уравнение х 2 + 6х + 9 = 0
А) 1 Б) 2 В) нет корней Г) определить невозможно
4. Решите уравнение х 2 — 2х — 15=0
А) корней нет Б) 3; -5 В) 1 Г) 5; -3
5. Решите уравнение 3х 2 — 3х + 4 = 0
А) 1 Б) 0; 4 В) корней нет Г) 0,5
6. Найдите наибольший корень уравнения –х 2 — 5х + 14 = 0
А) 2 Б) 7 В). 38 Г) корней нет.
7. Найдите сумму корней уравнения 6х 2 + 7х + 1=0
А) 1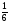 
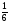
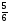
Б) -1 В) — 
Г) корней нет
8. Найдите произведение корней уравнения 2х 2 + 3х – 5 = 0:
А) -2,5 Б) -1,5 В) 2,5 Г) корней нет.
9. Найдите разность наибольшего и наименьшего из корней уравнения
А) 8 Б) 0 В) -8 Г) 32.
10. Решите уравнение 2х (х — 8) = — х — 18.
Тест «Решение квадратных уравнений по формуле»
Инструкция: В заданиях с 1 по 9 выберите только один правильный ответ из предложенных.
В задании 10 запишите решение и ответ.
1. Какое из квадратных уравнений является полным:
А) 5х 2 — 2х + 3 = 0 Б) 4х + 9х 2 = 0 В) 10х 2 = 0 Г) 6 — х 2 = 0
2. Дискриминант квадратного уравнения х 2 — 8х + 7 = 0 равен:
А) 92 Б) -36 В) 0 Г) 36
3. Сколько корней имеет квадратное уравнение х 2 + 5х + 9 = 0
А) 2 Б) нет корней В) 1 Г) определить невозможно
4. Решите уравнение х 2 + 2х – 15 = 0
А) Корней нет Б) 3; -5 В) 1 Г) 5; -3
5. Решите уравнение 4х 2 — 4х + 1 = 0
А) 1 Б) 0; 4 В) корней нет Г) 0,5
6. Найдите наименьший корень уравнения –х 2 + 7х – 10 = 0
А) -5 Б) 2 В) корней нет Г) 5
7. Найдите сумму корней уравнения 6х 2 — 7х + 1 = 0
А) 1,16 Б) корней нет В) 1 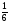Г)
8. Найдите произведение корней уравнения 2х 2 + 3х – 2 = 0
А) -1 Б) корней нет В) -2,5 Г) -10
9. Найдите разность наибольшего и наименьшего из корней уравнения
А) 6 Б) 0 В) 3 Г) — 6.
10. Решите уравнение 6х (2х + 1) = 5х + 1.
Тест «Решение квадратных уравнений по формуле»
📺 Видео
Как решать квадратные уравнения для чайниковСкачать
Теорема Виета за 30 сек🦾Скачать
Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать
Теорема Виета. 8 класс.Скачать
Неполные квадратные уравнения. Алгебра, 8 классСкачать
Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать
Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать
Алгебра 8. Урок 10 - Теорема Виета и её применение в задачахСкачать
Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать
Квадратные уравнения #shorts Как решать квадратные уравненияСкачать
Алгебра 9 класс. 8 сентября. квадратные уравненияСкачать
Квадратное уравнение. 8 класс.Скачать
