Каноническое уравнение в параметрическое онлайн

Этот онлайн-калькулятор выводит уравнения прямой в параметрической и канонической формах по двум заданным точкам на этой прямой.

Этот калькулятор может пригодиться для решения задач, где нужно вывести уравнения прямой, проходящей через две точки с заданными координатами. Просто введите координаты первой и второй точек, и калькулятор выведет параметрические и канонические уравнения прямой. Как обычно, теорию и формулы вы найдете под калькулятором

Видео:Написать канонические и параметрические уравнения прямой в пространствеСкачать

Онлайн калькулятор. Уравнение прямой проходящей через две точки

Этот онлайн калькулятор позволит вам очень просто найти параметрическое и каноническое уравнение прямой проходящей через две точки.

Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на составление уравнения прямой и закрепить пройденный материал.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Найти уравнение прямой

Выберите необходимую вам размерность:

Введите координаты точек.

Ввод данных в калькулятор для составления уравнения прямой

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для составления уравнения прямой

• Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.

Теория. Уравнение прямой.

Прямая — один из базовых элементов геометрии. Используя уравнения прямых можно существенно упростить решение многих задач.

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:Каноническое уравнение прямой в пространстве. 11 класс.Скачать

Уравнение прямой, проходящей через две точки онлайн

С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через две точки. Дается подробное решение с пояснениями. Для построения уравнения прямой задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точек в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:Параметрические уравнения прямойСкачать

Уравнение прямой, проходящей через две точки − примеры и решения

Пример 1. Построить прямую, проходящую через точки A(2, 1, 1), B(3, 1, -2).

(1)

Подставив координаты точек A и B в уравнение (1), получим:

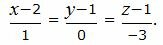(Здесь 0 в знаменателе не означает деление на 0).

Составим параметрическое уравнение прямой:

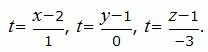Выразим переменные x, y, z через параметр t :

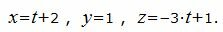Каноническое уравнение прямой, проходящей через точки A(2, 1, 1), B(3, 1, -2) имеет следующий вид:

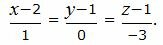Параметрическое уравнение прямой, проходящей через точки A(2, 1, 1), B(3, 1, -2) имеет следующий вид:

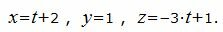Пример 2. Построить прямую, проходящую через точки A(1, 1/5, 1) и B(−2, 1/2, −2).

(2)

Подставив координаты точек A и B в уравнение (2), получим:

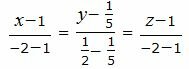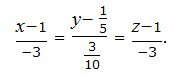Составим параметрическое уравнение прямой:

Выразим переменные x, y, z через параметр t :

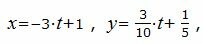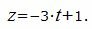Каноническое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:

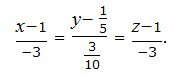Параметрическое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:

📹 Видео

Каноническое уравнение прямой в пространстве Преход от общего уравненияСкачать

Видеоурок "Параметрические уравнения прямой"Скачать

Видеоурок "Канонические уравнения прямой"Скачать

13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

Лекция 23. Виды уравнений прямой на плоскости.Скачать

Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

9 класс, 7 урок, Уравнение прямойСкачать

11. Прямая в пространстве и ее уравненияСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

12. Уравнения прямой в пространстве Решение задачСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Видеоурок "Общие уравнения прямой"Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать