Каноническое уравнение общего перпендикуляра прямых

Видео:Расстояние между скрещивающимися прямыми и уравнение их общего перпендикуляра.Скачать

Уравнение прямой, проходящей через заданную точку перпендикулярно заданной прямой

В данной статье научимся составлять уравнения прямой, проходящей через заданную точку на плоскости перпендикулярно заданной прямой. Изучим теоретические сведения, приведем наглядные примеры, где необходимо записать такое уравнение.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Принцип составления уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой

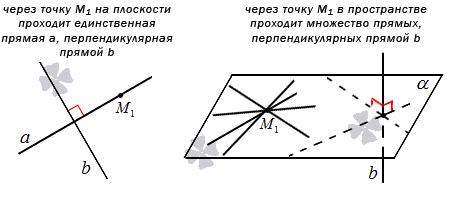
Перед нахождением уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой. Теорема рассматривается в средней школе. Через заданную точку, лежащую на плоскости, можно провести единственную прямую, перпендикулярную данной. Если имеется трехмерное пространство, то количество таких прямых увеличится до бесконечности.

Если плоскость α проходит через заданную точку М 1 перпендикулярно к заданной прямой b , то прямые, лежащие в этой плоскости, в том числе и проходящая через М 1 являются перпендикулярными заданной прямой b .

Отсюда можно прийти к выводу, что составление уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой применимо только для случая на плоскости.

Задачи с трехмерным пространством подразумевают поиск уравнения плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.

Если на плоскости с системой координат О х у z имеем прямую b , то ей соответствует уравнение прямой на плоскости, задается точка с координатами M 1 ( x 1 , y 1 ) , а необходимо составить уравнение прямой a , которая проходит через точку М 1 , причем перпендикулярно прямой b .

По условию имеем координаты точки М 1 . Для написания уравнения прямой необходимо иметь координаты направляющего вектора прямой a , или координаты нормального вектора прямой a , или угловой коэффициент прямой a .

Необходимо получить данные из заданного уравнения прямой b . По условию прямые a и b перпендикулярные, значит, направляющий вектор прямой b считается нормальным вектором прямой a . Отсюда получим, что угловые коэффициенты обозначаются как k b и k a . Они связаны при помощи соотношения k b · k a = — 1 .

Получили, что направляющий вектор прямой b имеет вид b → = ( b x , b y ) , отсюда нормальный вектор — n a → = ( A 2 , B 2 ) , где значения A 2 = b x , B 2 = b y . Тогда запишем общее уравнение прямой, проходящее через точку с координатами M 1 ( x 1 , y 1 ) , имеющее нормальный вектор n a → = ( A 2 , B 2 ) , имеющее вид A 2 · ( x — x 1 ) + B 2 · ( y — y 1 ) = 0 .

Нормальный вектор прямой b определен и имеет вид n b → = ( A 1 , B 1 ) , тогда направляющий вектор прямой a является вектором a → = ( a x , a y ) , где значения a x = A 1 , a y = B 1 . Значит осталось составить каноническое или параметрическое уравнение прямой a , проходящее через точку с координатами M 1 ( x 1 , y 1 ) с направляющим вектором a → = ( a x , a y ) , имеющее вид x — x 1 a x = y — y 1 a y или x = x 1 + a x · λ y = y 1 + a y · λ соответственно.

После нахождения углового коэффициента k b прямой b можно высчитать угловой коэффициент прямой a . Он будет равен — 1 k b . Отсюда следует, что можно записать уравнение прямой a , проходящей через M 1 ( x 1 , y 1 ) с угловым коэффициентом — 1 k b в виде y — y 1 = — 1 k b · ( x — x 1 ) .

Полученное уравнение прямой, проходящее через заданную точку плоскости перпендикулярно заданной. Если того требуют обстоятельства, можно переходить к другому виду данного уравнения.

Видео:Видеоурок "Канонические уравнения прямой"Скачать

Решение примеров

Рассмотрим составление уравнения прямой, проходящей через заданную точку плоскости и перпендикулярно заданной прямой.

Записать уравнение прямой а, которая проходит через точку с координатами M 1 ( 7 , — 9 ) и перпендикулярна прямой b , которое задано каноническим уравнением прямой x — 2 3 = y + 4 1 .

Из условия имеем, что b → = ( 3 , 1 ) является направляющим вектором прямой x — 2 3 = y + 4 1 . Координаты вектора b → = 3 , 1 являются координатами нормального вектора прямой a , так как прямые a и b взаимно перпендикулярны. Значит, получаем n a → = ( 3 , 1 ) . Теперь необходимо записать уравнение прямой, проходящее через точку M 1 ( 7 , — 9 ) , имеющее нормальный вектор с координатами n a → = ( 3 , 1 ) .

Получим уравнение вида: 3 · ( x — 7 ) + 1 · ( y — ( — 9 ) ) = 0 ⇔ 3 x + y — 12 = 0

Полученное уравнение является искомым.

Ответ: 3 x + y — 12 = 0 .

Составить уравнение прямой, которая проходит через начало координат системы координат О х у z , перпендикулярно прямой 2 x — y + 1 = 0 .

Имеем, что n b → = ( 2 , — 1 ) является нормальным вектором заданной прямой. Отсюда a → = ( 2 , — 1 ) — координаты искомого направляющего вектора прямой.

Зафиксируем уравнение прямой, проходящую через начало координат с направляющим вектором a → = ( 2 , — 1 ) . Получим, что x — 0 2 = y + 0 — 1 ⇔ x 2 = y — 1 . Полученное выражение является уравнение прямой, проходящей через начало координат перпендикулярно прямой 2 x — y + 1 = 0 .

Ответ: x 2 = y — 1 .

Записать уравнение прямой, проходящей через точку с координатами M 1 ( 5 , — 3 ) перпендикулярно прямой y = — 5 2 x + 6 .

Из уравнения y = — 5 2 x + 6 угловой коэффициент имеет значение — 5 2 . Угловой коэффициент прямой, которая перпендикулярна ей имеет значение — 1 — 5 2 = 2 5 . Отсюда делаем вывод, что прямая, проходящая через точку с координатами M 1 ( 5 , — 3 ) перпендикулярно прямой y = — 5 2 x + 6 , равна y — ( — 3 ) = 2 5 · x — 5 ⇔ y = 2 5 x — 5 .

Видео:Написать канонические и параметрические уравнения прямой в пространствеСкачать

Общий перпендикуляр к двум скрещивающимся прямым. Расстояние между скрещивающимися прямыми

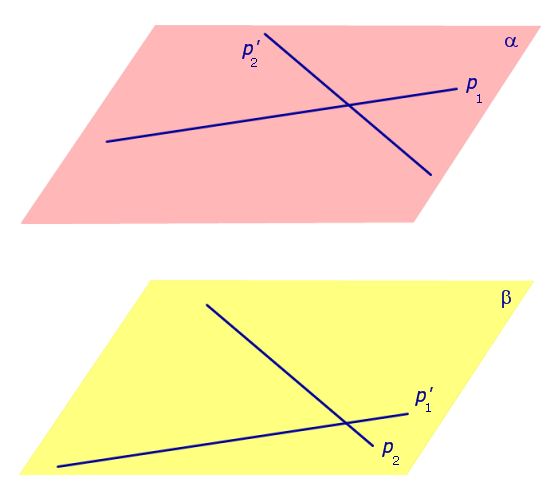
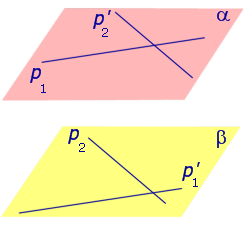
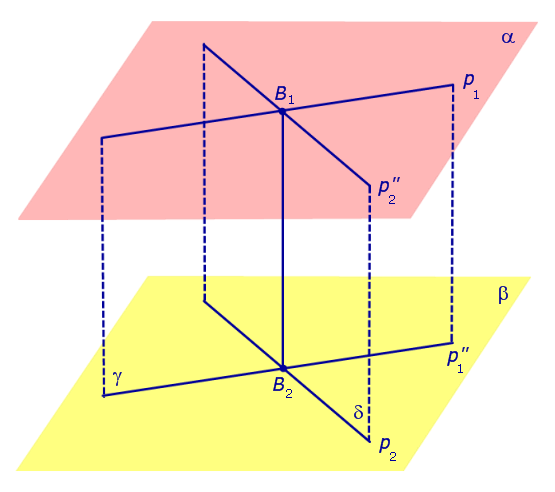
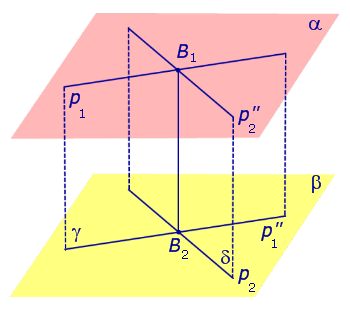
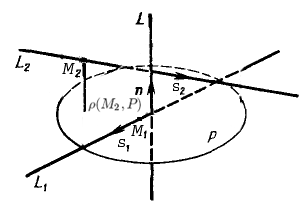
Теорема. Пусть p₁ и p₂ – две произвольные скрещивающиеся прямые скрещивающиеся прямые . Если рассмотреть всевозможные прямые A₁A₂, такие, что точка A₁ лежит на прямой p₁, а точка A₂ лежит на прямой p₂, то будут выполнены следующие два утверждения:

1. Среди всех прямых A₁A₂ существует единственная прямая, перпендикулярная к прямой p₁ и к прямой p₂ ( общий перпендикуляр к двум скрещивающимся прямым ).
2. Среди всех отрезков A₁A₂наименьшую длину имеет отрезок общего перпендикуляра к двум скрещивающимся прямым.

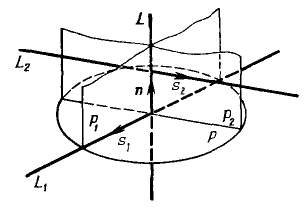
Доказательство. Докажем сначала существование общего перпендикуляра к двум скрещивающимся прямым.

Через произвольную точку прямой p₁ проведем прямую , параллельную прямой параллельную прямой p₂ , а через произвольную точку прямой p₂ проведем прямую , параллельную прямой параллельную прямой p₁ . Обозначим буквой α плоскость, проходящую через прямые p₁ и , а буквой β плоскость, проходящую через прямые p₂ и (рис 1).

Поскольку прямая p₁ параллельна прямой , лежащей на плоскости β , то по признаку параллельности прямой и плоскости прямая p₁ параллельна плоскости β. Точно так же, поскольку прямая параллельна прямой p₂ , лежащей на плоскости β , то прямая по признаку параллельности прямой и плоскости параллельна плоскости β. Таким образом, плоскость α содержит две пересекающиеся прямые p₁ и , паралельные плоскости β. В силу признака параллельности плоскостей заключаем, что плоскости α и β параллельны.

Спроектируем прямую p₁ на плоскость β. Получим прямую , являющуюся проекцией прямой проекцией прямой p₁, и обозначим точку пересечения прямых p₂ и буквой B₂ (рис. 2).

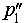
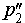
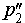
Спроектируем теперь прямую p₂ на плоскость α . Получим прямую , являющуюся проекцией прямой проекцией прямой p₂ , и обозначим точку пересечения прямых p₁ и буквой B₁ (рис. 3).

Доказательство существования общего перпендикуляра к двум скрещивающимся прямым завершено.

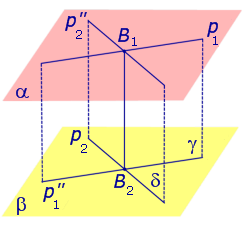
Докажем, что построенная прямая B₁B₂ является единственным общим перпендикуляром к прямым p₁ и p₂ .

Таким образом, общий перпендикуляр к прямым p₁ и p₂ является линией пересечения плоскостей γ и δ, то есть прямой B₁B₂ .

Доказательство единственности общего перпендикуляра к двум скрещивающимся прямым завершено. Утверждение 1 доказано.

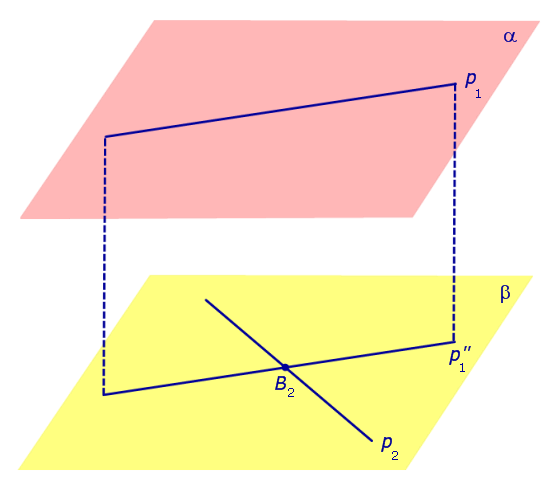
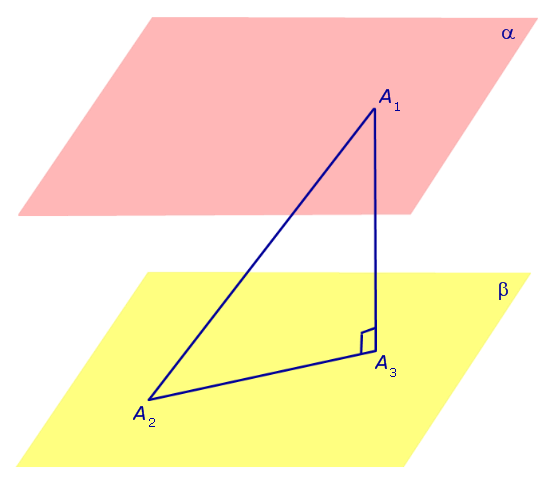
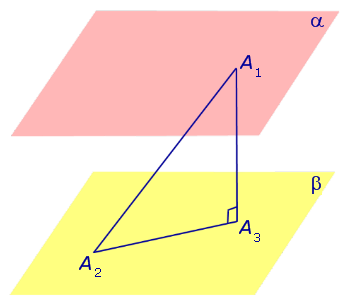
Перейдем к доказательству утверждения 2. Для этого рассмотрим произвольный отрезок A₁A₂ , у которого конец A₁ лежит на плоскости α , а конец A₂ лежит на плоскости β . Опустим перпендикуляр из точки A₁ на плоскость β и обозначим основание этого перпендикуляра символом A₃ (рис. 4).

Если отрезок A₁A₂ не является перпендикуляром к плоскостям α и β, то точка A₃ не совпадет с точкой A₂ , и треугольник A₁A₂A₃ будет прямоугольным треугольником с гипотенузой A₁A₂ и катетом A₁A₃. Поскольку в прямоугольном треугольнике длина катета меньше длины гипотенузы, то

Видео:Каноническое уравнение прямой в пространстве Преход от общего уравненияСкачать

Математический портал

Видео:12. Уравнения прямой в пространстве Решение задачСкачать

Nav view search

Navigation

Search

• Вы здесь:
• Home

Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Расстояние между двумя скрещивающимися прямыми.

Пусть $L_1: frac=frac=frac$ и $L_2: frac=frac=frac$ — две скрещивающиеся прямые. Расстояние $rho(L_1, L_2)$ между прямыми $L_1$ и $L_2$ можно найти по следующей схеме:

1) Находим уравнение плоскости $P,$ проходящей через прямую $L_1,$ параллельно прямой $L_2:$

Плоскость $P$ проходит через точку $M_1(x_1, y_1, z_1),$ перпендикулярно вектору $overline n=[overline s_1, overline s_2]=(n_x, n_y, n_z),$ где $overline s_1=(m_1, l_1, k_1)$ и $overline s_2=(m_2, l_2, k_2)$ — направляющие вектора прямых $L_1$ и $L_2.$ Следовательно, уравнение плоскости $P: n_x(x-x_1)+n_y(y-y_1)+n_z(z-z_1)=0.$

2) Расстояние между прямыми $L_1$ и $L_2$ равно расстоянию от любой точки прямой $L_2$ до плоскости $P:$

Нахождение общего перпендикуляра скрещивающихся прямых.

Для нахождения общего перпендикуляра прямых $L_1$ и $L_2,$ необходимо найти уравнения
плоскостей $P_1$ и $P_2,$ проходящих, соответственно, через прямые $L_1$ и $L_2,$ перпендикулярно плоскости $P.$

Пусть $P_1: A_1x+B_1y+C_1z+D_1=0;$

Тогда уравнение общего перпендикуляра имеет вид

Пример.

2.214.

а) доказать, что прямые не лежат в одной плоскости, то есть являются скрещивающимися;

б) написать уравнение плоскости, проходящей через прямую $L_2$ параллельно $L_1;$

в) вычислить расстояние между прямыми;

г) написать уравнения общего перпендикуляра к прямым $L_1$ и $L_2.$

Решение.

а) Если прямые $L_1$ и $L_2$ лежат в одной плоскости, то их направляющие вектора $overline(3, 4, -2),$ $overline(6, -4, -1),$ и вектор $overline l,$ соединяющий произвольную точку прямой $L_1$ и произвольную точку прямой $L_2$ компланарны. В качестве такого вектора $overline$ можно выбрать $overline(x_2-x_1, y_2-y_1, z_2-z_1).$ Проверим будут ли эти вектора компланарны.

Следовательно, вектора не компланарны и прямые не лежат в одной плоскости.

б) Запишем уравнение плоскости, проходящей через прямую $L_2$ параллельно $L_1.$ Эта плоскость проходит через точку $M_2(21, -5, 2)$ перпендикулярно вектору $overline n=[overline s_1, overline s_2].$

Таким образом, вектор $overline n$ имеет координаты $overline n(-12, -9, -36).$

Находим уравнение плоскости $$P:,, -12(x-21)-9(y+5)-36(z-2)=0Rightarrow$$ $$Rightarrow-12x-9y-36z+252-45+72=0Rightarrow -12x-9y-36z+279=0Rightarrow$$ $$Rightarrow 4x+3y+12z-93=0.$$

в) Расстояние между прямыми $L_1$ и $L_2$ равно расстоянию от любой точки прямой $L_1$ до плоскости $P:$

Ответ: $frac.$

г) Найдем уравнения плоскостей $P_1$ и $P_2,$ проходящих, соответственно, через прямые $L_1$ и $L_2,$ перпендикулярно плоскости $P.$

Имеем, $M_1=(-7, -4, -3)in P_1,$

Таким образом, $$P_1: 54(x+7)-44(y+4)-7(z+3)=54x-44y-7z+378-176-21=$$ $$=54x-44y-7z+181=0.$$

Аналогично находим $P_2:$

Имеем, $M_2=(21, -5, 2)in P_2,$

Таким образом, $$P_1: -45(x-21)-76(y+5)+34(z-2)=-45x-76y+34z+945-380-68=$$ $$=-45x-76y+34z+497=0.$$

Ответ: $left<begin54x-44y-7z+181=0;\ -45x-76y+34z+497=0.endright. $

2.215.

а) доказать, что прямые не лежат в одной плоскости, то есть являются скрещивающимися;

б) написать уравнение плоскости, проходящей через прямую $L_2$ параллельно $L_1;$

в) вычислить расстояние между прямыми;

г) написать уравнения общего перпендикуляра к прямым $L_1$ и $L_2.$

Ответ: б) $4x+12y+12z+76=0;$

г) $left<begin53x-7y-44z-429=0;\ 105x-23y-48z+136=0.endright. $

🌟 Видео

Построение общего перпендикуляра к двум скрещивающимся прямым | Стереометрия #33 | ИнфоурокСкачать

Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Видеоурок "Общие уравнения прямой"Скачать

Видеоурок "Параметрические уравнения прямой"Скачать

13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Лекция 23. Виды уравнений прямой на плоскости.Скачать

11. Прямая в пространстве и ее уравненияСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

9 класс, 7 урок, Уравнение прямойСкачать