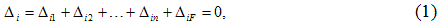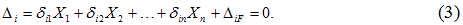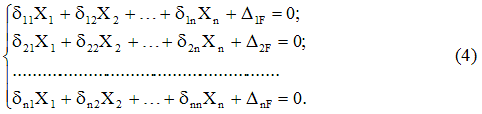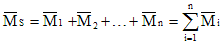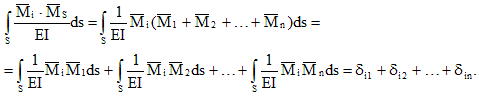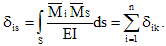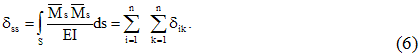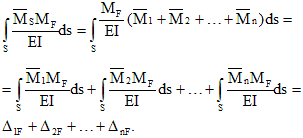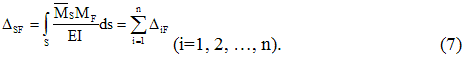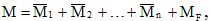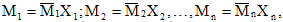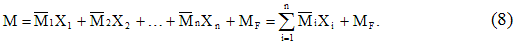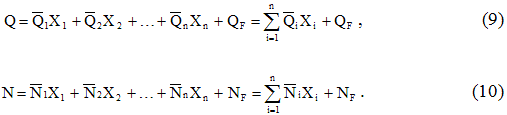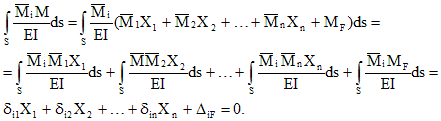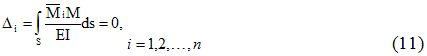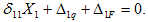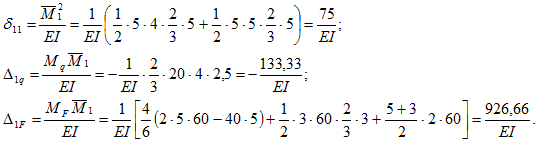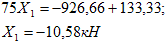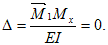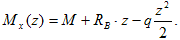Каноническое уравнение метода сил для один раз статически неопределимой системы (2 видео)

Канонические уравнения метода сил. Выбор основной системы

При расчете статически неопределимых систем с помощью метода сил надо отбросить «лишние» связи и образовать так называемую основную систему, которая должна быть статически определимой и геометрически и мгновенно неизменяемой. Основных систем может быть несколько; из них выбирается наиболее удобная для расчета.

В основной системе надо приложить по направлению реакций в отброшенных (устраненных) связях неизвестные силы или моменты Х_<, Х₂, . Х_п. Поставив условие, что основная система должна деформироваться как заданная, надо приравнять нулю линейные и угловые перемещения по направлению реакций в отброшенных связях от совместного действия нагрузки и всех неизвестных. Таким образом, можно составить дополнительные уравнения (уравнения перемещений), которые позволяют определить все неизвестные метода сил.

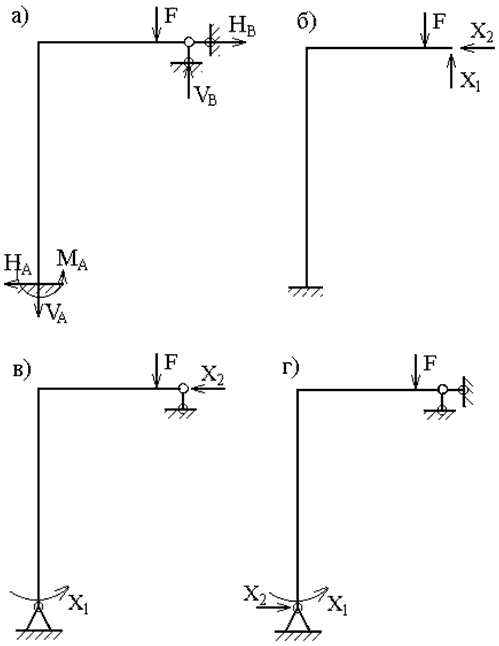
Рассмотрим, например, один раз статически неопределимую балку (рис. 10.8, а). Отбрасывая «лишнюю» связь, образуем основные системы и составим соответствующие дополнительные уравнения.

Для образования первой основной системы (рис. 10.8, б) отброшена шарнирная опора В. Дополнительное уравнение должно выражать условие равенства нулю прогиба в сечении В от совместного действия заданной нагрузки и неизвестной силы Х_х = R_B. На основании принципа независимости действия сил представим это уравнение в следующем виде:

где v_BP и v_BX] — соответственно прогибы балки в сечении В от действия заданной нагрузки и неизвестной силы Х_<.

Для образования второй основной системы (рис. 10.8, в) жесткая заделка в сечении А заменена шарнирно неподвижной опорой. В качестве неизвестного принят реактивный момент в заделке. Дополнительное уравнение должно выражать условие равенства нулю угла поворота в сечении А от совместного действия нагрузок и неизвестного опорного момента Х_х = М_А

Для образования третьей основной системы (рис. 10.8, г) в сечении С введен промежуточный шарнир. Дополнительное уравнение составим из условия равенства углов поворота в заданной балке слева и справа от сечения С, т.е. из условия равенства нулю взаимного угла поворота сечения Дср_с:

Неизвестный момент = М_с, приложенный в основной системе слева и справа от шарнира С, называется парным неизвестным.

Дополнительные уравнения удобно записать в специальной, так называемой канонической форме метода сил. Рассмотрим, например, два раза статически неопределимую балку (рис. 10.9, а). Для образования основной системы введем в сечении А вместо жесткой заделки шарнирно-неподвижную опору и отбросим опору В. По направлению реакций в отброшенных связях приложим неизвестный момент Х = М_А и неизвестную силу Х₂ = R_B (рис. 10.9, б).

Поставив деформацию основной системы в соответствие с деформацией заданной балки, приравняем нулю угол поворота на опоре А и прогиб в сечении В. Дополнительные уравнения запишем в следующем виде:

В этих уравнениях А_п, Д₁₂, Л₂₁ и Д₂₂ — перемещения в основной системе по направлению реакций в отброшенных связях от действия неизвестных Х₁ и Х₂. Их можно представить в следующем виде:

где 5_П, б₁₂, 5₂₁, 6₂₂ — перемещения в основной системе по направлению реакций в отброшенных связях от действия единичных нагрузок X] = 1 и Х₂ = 1 (рис. 10.9, в, г). На основании теоремы Максвелла о взаимности перемещений величины 6₁₂ и §₂₁ численно равны между собой: 6₁₂ = 6₂₁.

Величины А_1Р и А_2Р представляют собой перемещения в основной системе по направлению реакций в отброшенных связях от действия заданной нагрузки (рис. 10.9, д).

Таким образом, дополнительные уравнения примут следующий вид:

Обобщая рассмотренную форму записи, можно составить п канонических уравнений для п раз статически неопределимой балки или стержневой системы:

Каждое из канонических уравнений (10.3) характеризует условие равенства нулю линейных или угловых перемещений в основной системе по направлению реакций в отброшенных связях. Величины b_ik (/, к = 1, 2, . п) называются коэффициентами системы (10.3), a A_iP — грузовыми или свободными членами. Поскольку они представляют собой перемещения в основной системе, для их определения обычно используется формула Мора. Для систем, работающих преимущественно на изгиб (балки и рамы), они определяются по формулам:

где Mj и М_к — изгибающие моменты в основной системе от действия единичных сил или моментов Х_х? = 1, приложенных по направлению неизвестных; М_р — изгибающий момент в основной системе от действия заданных нагрузок.

При расчете статически неопределимых ферм коэффициенты и грузовые члены определяются по формулам:

где N_p N_k, и N_p — продольные силы в стержнях основной системы от действия единичных сил и заданных нагрузок. Расчет статически неопределимых ферм удобно проводить в табличной форме.

Интегрирование в формулах (10.4) и (10.5) производится в пределах длины каждого стержня, а суммирование — по всем стержням системы.

Коэффициенты §ц, §22’ •••’ называются главными коэффициентами. Они всегда являются положительными. Коэффициенты 6,₂, §2), •••, §/? (/ Ф к) называются побочными коэффициентами. Для них на основании теоремы Максвелла о взаимности перемещений справедливо равенство

Побочные коэффициенты и грузовые члены A_jP могут быть положительными, отрицательными и равными нулю.

Для прямых стержней постоянной жесткости (EJ = const) вычисление коэффициентов и грузовых членов обычно производится с помощью «перемножения» единичных и грузовой эпюр Mj и М_р по правилу Верещагина.

Структура системы канонических уравнений не зависит от выбора основной системы, а их число равно степени статической неопределимости заданной системы. При этом для каждой основной системы будут свои значения коэффициентов и грузовых членов.

Решение системы канонических уравнений (10.3) позволяет определить все неизвестные метода сил. Если величина какого- либо неизвестного оказалась отрицательной, то его направление надо изменить на противоположное.

Рассмотрим подробнее вопросы образования основной системы. Как правило, она выбирается статически определимой, хотя возможно использование статически неопределимой основной системы, если для нее имеются готовые решения.

При образовании основной системы устранение «лишних» связей может быть произведено путем отбрасывания опор, введения опорных или промежуточных шарниров, рассечения стержней. При этом необходим кинематический и структурный анализ основной системы для исключения ее геометрической и мгновенной изменяемости. Рассмотрим примеры.

При образовании основной системы для два раза статически неопределимой рамы (рис. 10.10, а) нельзя устранить горизонтальную связь на опоре В, поскольку в этом случае рама может свободно перемещаться в горизонтальном направлении. Основная система на рис. 10.10, б является неправильной. Одна из возможных основных систем приведена на рис. 10.10, в.

Для один раз статически неопределимой рамы (рис. 10.11, а) основная система 10.11, б является мгновенно изменяемой и не может быть использована. Правильная основная система приведена на рис. 10.11, в.

При удачном выборе основной системы часть побочных коэффициентов S_ik (/ ф к) и грузовых членов обращаются в нуль, что существенно упрощает решение. Это имеет место, например, для систем, имеющих ось симметрии. При этом неизвестные метода сил надо разложить на симметричные и кососимметричные парные составляющие.

Рассмотрим, например, два раза статически неопределимую раму, имеющую вертикальную ось симметрии (рис. 10.12, а). При образовании основной системы отбросим опоры А и С и разложим неизвестные опорные реакции У_А и У_с на симметричные и кососимметричные групповые неизвестные Х_< и Х₂ (рис. 10.12, б). При этом V_A=X_l +Х₂, V_c = X_l-X₂.

Такой прием называется группировкой неизвестных. Соответствующие единичные эпюры приведены на рис. 10.12, в, г. Эпюра Mj является симметричной относительно вертикальной оси, а эпюра М₂ — кососимметричной. Очевидно, что результат «перемножения» этих эпюр между собой равен нулю:

При этом система канонических уравнений относительно групповых неизвестных Х_< и Х₂ распадается на два независимых уравнения:

При наличии оси симметрии к упрощению расчета может привести представление нагрузки в виде суммы симметричной и кососимметричной составляющих. Расчет производится раздельно на действие этих составляющих, а результаты суммируются.

Для рассмотренной выше рамы такое разложение силы Р показано на рис. 10.13, а, б. На этом рисунке приведены также соответствующие грузовые эпюры для принятой основной системы.

Очевидно, что при симметричном нагружении А_2Р = 0 («перемножение» симметричной и кососимметричной эпюр) и система канонических уравнений принимает следующий вид:

При симметричном нагружении кососимметричное групповое неизвестное Х₂ = 0. Аналогично для кососимметричного нагружения имеем А_1Р = 0 и Х_х = 0.

Содержание

Канонические уравнения метода сил
Метод сил — расчет статически неопределимых рам
Канонические уравнения метода сил
Алгоритм расчета методом сил
Выбор основной системы
Вычисление коэффициентов и свободных членов канонических уравнений
Универсальная проверка коэффициентов и свободных членов канонических уравнений
Построение окончательных эпюр внутренних силовых факторов
Проверка окончательной эпюры изгибающих моментов
Определение перемещений в статически неопределимых системах
Пример расчета
📺 Видео

Видео:Расчет статически неопределимой рамы методом силСкачать

Канонические уравнения метода сил

Используя всё выше изложенное, можно приступить к составлению уравнений, описывающих особенности работы статически неопределимых рам и балок.

Статически неопределимые рамы.

Подробный разбор раскрытия статической неопределимости у рам.

На рис. 12,а изображена плоская статически неопределимая рама с защемлёнными концами.

Эта рама трижды статически неопределима. Наиболее рациональным вариантом эквивалентной системы будет вариант, приведенный на рис. 12,б. Заданная конструкция рамы предполагает, что перемещения в точке В (защемлены) по всем трём направлениям (1,2,3) отсутствуют, т.е.

В развёрнутом виде это может быть записано следующим образом:

Полученная система уравнений носит название системы канонических уравнений метода сил. Для её решения необходимо построить эпюры изгибающих моментов от внешней нагрузки (грузовая эпюра) (рис. 12,в) и единичных усилий (Х1=1; Х2=1; Х3=1;) (рис. 12,г) и пользуясь методом Мора вычислить коэффициенты канонических уравнений (если возможно воспользоваться способом Верещагина)

В рассматриваемом примере:

При определении коэффициентов необходимо помнить следующее:

Коэффициенты, имеющие двойные одинаковые индексы, называются главными. Они вычисляются умножением эпюр от единичных нагрузок самих на себя. Эти коэффициенты всегда положительны.

Коэффициенты имеющие разные индексы, называются побочными. Они вычисляются умножением эпюр от разных единичных сил друг на друга и могут быть положительными, отрицательными, нулевыми. Коэффициенты: и т.д. — попарно равны между собой (на основании теоремы о взаимности перемещений).

Грузовые коэффициенты вычисляются умножением грузовой эпюры соответствующую единичную. При вычислении грузовых коэффициентов площади всегда берутся с криволинейной эпюры, а ордината под её центром тяжести — с линейной. Эти коэффициенты могут быть: положительными, отрицательными, нулевыми.

Найденные значения коэффициентов необходимо подставить в систему уравнений и решить последнюю.

Задача считается решённой, если найдены значения всех неизвестных и построена суммарная эпюра изгибающих моментов. построение суммарной эпюры может быть выполнено двумя способами.

При первом способе построения основную систему нагружают внешними нагрузками и найденными значениями неизвестных усилий (рис. 12,д). Если в результате решения системы уравнений, оказалось, что какое-то из неизвестных имеет знак минус (в нашем случае Х2= -3р/64), то при нагружении этим усилием основной системы необходимо изменить его направление на противоположенное. Дальнейшее построение эпюры изгибающих моментов выполняется по общим правилам, т.е. для каждого участка рамы записываются уравнения изгибающих моментов и производятся соответствующие подсчёты.

Рама, представленная на рис. 12,д имеет три участка, для которых могут быть записаны следующие уравнения:

Суммарная эпюра изгибающих моментов представлена на рис. 12,е.

При другом способе построения, эпюра М? , построенных от действительных значений Х1;Х2 и т.д., найденных при решении системы уравнений, и грузовой эпюры. В нашем случае: эпюры от Х1;Х2;Х3; (рис. 12,ж) и эпюры от внешних нагрузок (рис. 12,в).

Суммирование производится по точкам. Точка В

Найденные значения соответствуют вычисленным ранее при построении суммарной эпюры первым способом (рис. 12, е).

Проверка правильности полученного решения.

Известно, что перемещение по напровлению действия связи должно отсутствовать. Это условие и используется при проверке.

Для исследуемой рамы выбирают новую основную систему (рис. 13,а) и нагружают её единичной нагрузкой, действующей по направлению одной из отброшенных связей (рис. 13,б). От действия этой нагрузки строят единичную эпюру (рис. 13,в). Эту эпюру по правилу Верещагина перемножают с эпюрой М (рис. 12,е); результат перемножения должен дать 0. В ряде случаев непосредственное вычисление площадей элементов суммарной эпюры и определение их центров тяжести бывает затруднительно.

Поэтому перемножение суммарной эпюры на единичную можно заменить перемножением составляющих суммарной эпюры (рис. 12,в,ж) на единичную (рис. 13,в) с последующим суммированием результатов.

Угол поворота сечения в точке А (рис. 12) оказался равным нулю, что соответствует действительности, т.к. углы поворота защемлениях отсутствуют.

Пример расчёта статически неопределимых рам.

Пример I. Для рамы, изображённой на фиг. 14,а требуется раскрыть статическую неопределимость и построить суммарную эпюру изгибающих моментов. Моменты инерции стоек рамы и её горизонтального элемента (ригеля) различны и показаны на чертеже. Число неизвестных опорных реакций, рассматриваемой рамы, равно пяти, так что две из них являются «лишними». Основная и эквивалентная системы, а так же эпюры изгибающих моментов от заданной нагрузки и от лишних неизвестных Х1 и Х2 = 1 показаны на фиг. 14,б, в, г, д, е. Канонические уравнения метода сил имеют вид:

Коэффициенты этих уравнений вычислим по формуле Верещагина:

Подставим найденные значения коэффициентов в систему канонических уравнений и решим последнюю.

После этого одним из выше указанных методов строим суммарную эпюру изгибающих моментов (фиг. 15).

Пример II. Для рамы изображённой на фиг.16,а, требуется раскрыть статическую неопределимость и построить суммарную эпюру изгибающих моментов.

Число неизвестных опорных реакций рассматриваемой рамы равно четырём, так что одна из них является лишней.

Основная и эквивалентная системы, эпюры от заданных нагрузок и эпюра от Х1 =1 показаны на фиг.16,б,в,г,д,е.

Каноническое уравнение метода сил имеет вид:

Коэффициенты будем определять по правилу Верещагина.

Подставим найденые коэффициенты в каноническое уравнение получим:

Строим сумарную эпюру изгибающих моментов (фиг. 17,а,б)

Пример 3. Дана статически неопределимая рама симметричной конструкции с симметричным нагружением (рис.18,а).

Необходимо построить суммарную эпюру изгибающих моментов проверить правельность решения.

Эта рама три раза статически неопределима.

В качестве лишних неизвестных выступают внутренние силовые факторы на оси симмтрии (рис.18,б и рис.18,в):

изгибающий момент X1,

пордольная сила X2,

поперечная сила X3.

Относительно оси симметрии X1 и Х2 являются симметричными нагрузками; Х 3 — кососимметричной нагрузкой.

Составим систему канонических уравнений

и построим соответствующие эпюры изгибающих моментов отединичных сил (рис.18, г) и внешних нагрузок (рис.18, д).

При подсчётах получается, что .

Таким образом, за счёт рационального выбора основной системы, система канонических уравнений значительно упростилась. Это позваляет сформулировать следующие правило: если система симметрична и для её расчёта выбрана симметричная основная система, то при действии симметричной нагрузки кососимметричные неизвестные обращаются в нуль.

Перестраиваем эпюры от Х1 и Х2 (рис.18, е) и строим суммарную эпюру (рис.18,ж).

Проверяем правильность полученного решения.

Если задача решена верно, то угол поворота на опоре В должен отсутствовать.

Выбераем новую основную систему для чего отбрасываем на опоре В три «лишних» связи: горизонтальную и вертикальную составляющие реакции и реактивный момент (рис.18, з). Заменяем действие одной из отброшенных связей (в нашем примере — момента) единичной нагрузкой (рис.18, и) и стороим эпюру изгибающих моментов от действия этой нагрузки (рис.18, к).

Определяем угол поворота на опоре В

следовательно задача решена верно.

Дана статически неопределимая рама симетричной конструкции с кососимметричным нагружением (рис.19, а). Построить суммарную эпюру изгибающих моментов.

Эта рама, как и в предыдущем случае, три раза статически неопределима, т. е. Для решения задачи необходимо записать систему из трёх уравнений с тремя неизвестными. (См. Предыдущий пример).

Коэффициенты при неизвестных в этих уравнениях определяются по общему правилу. Эпюры изгибающих моментов от сил Х1 = 1; Х2=1; Х3=1 такие же, как в примере 3 (рис.18, г), а грузовая эпюра представлена на рис. 19, д.

При определение коэффициентов получается, что

Тогда система канонических уравнений примет вид:

Первые два уравнения имеют только нулевое решение:

Х1=0 и Х2=0; таким образом, остаётся одно уравнение с одним неизвестным:

Итак, если система симметрична и для её расчёт выбрана симмтричная основная симметричные неизвестные обращаются в нуль.

Строим суммарную эпюру изгибающих моментов (рис. 19, е).

Дана статически неопределимая рама симметричной конструкции с произвольными нагружением (рис. 20, а).

Построить эпюру изгибающих моментов, возникабщих в элементах рамы.

Эта рама трижды статически неопределима. Данная задача имеет два варианта решения. По первому варианту исходная задача может быть разбита на две более простых (рис. 20, б), решения которых будут анфлогичны приведённым в предыдущих примерах (3 и 4). Схема решения по второму варианту приведена на рис. 20,в,г.

В этом случае система трёх уравнений с тремя неизвестными имеет ряд нулевых коэффициентов и значительно упрощается:

Решая систему уравнений получаем:

Проверка подтверждает правильность полученного решения.

Суммарная эпюра изгибающих моментов представлена на рис. 20, д.

Статически неопределимые балки.

На рис. 21,а изображена балка один раз статическм неопределимая. Для этой балки за «лишнее» неизвестное удобнее всего принять реакцию, которая возникает на опоре В при действии внешней нагрузки Р.

Тогда основная система (см. Раздел 2.2) принимает вид консольной балки (рис. 21, б), а эквивалентная — этой же балки нагруженной внешним усилием Р и неизвестной опорой Х1 (рис. 21, в). Система, представленная на рис. 21, в будет эквивалентна заданой, если сила Х1 будет подобрана так, что вертикальное перемещение на опоре В будет отсутствовать. Это условие может быть записано в виде канонического уравнения метода сил:

Как и в предыдущих примерах, коэффициенты канонического уравнения определяем по способу Верещагина, построив предварительно эпюру изгибающих моментов от внешней нагрузки (рис. 21, г) и Х1=1 (рис. 21, д)

По одному из рассмотренных ранее (стр. 13) способов, строим суммарную эпюру изгибающих моментов (суммарная эпюра изгибающих моментов представлена на рис. 21, е).

Проверка правельности решения.

Известно, что угол поворота сечения в заделке равен 0. Определим этот угол поворота в сечении А балки АВ изображённой на рис. 21. Для этого выберем новую основную систему и нагрузим её единичным усилием, действубщим по направлению отброшенной связи (рис. 22, а).

Эпюра изгибающих моментов от этого усилия представлена на рис. 22, б. Перемножим по правилу верещагина эпюры, представленные на рис. 21, е и 22, б. Использовав расслоение:

площади элементов расслоений эпюры. уС1; уС2; уС3 — ординаты взятые под центрами тяжести этих площадей.

Угол поворота в заделке равен 0 — задача решена верно.

Примера расчёта статически неопределимых балок.

Дана один раз статически неопределимая балка (рис. 23, а). Необходимо раскрыть статическую неопределимость эпюру изгибающих моментов.

Считаем среднюю опору «лишней» и заменяем её действие силой Х1.

Система, эквивалентная заданной, представленной на рис. 23,б. Составим каноническое уравнение метода сил, смысл которого сводится к следующему: вертикальное перемещение в точке В эквивалентной системы от совместного действия сил Р и Х должно быть равно нулю, т. к. В исходной схеме вертикальное перемещение на опоре В отсутствует.

Строим эпюры изгибающих моментов от сил Р (рис. 23, в) и силы = 1 (рис.23,г); определяем коэффициенты канонического уравнения.

Строим суммарную эпюру изгибающих моментов.

Видео:канонические уравнения метода силСкачать

Метод сил — расчет статически неопределимых рам

При решении задач сопромата, статически неопределимой называется такая система, которая не может быть рассчитана при помощи одних только уравнений статики, так как имеет лишние связи. Для расчета таких систем составляются дополнительные уравнения, учитывающие деформации системы.

Оговоримся, что здесь и далее понятие “расчет” подразумевает только построение эпюр внутренних силовых факторов, возникающих в элементах системы, а не расчет на прочность, жесткость и т.д.

Статически неопределимые системы обладают рядом характерных особенностей:

1. Статически неопределимые конструкции являются более жесткими, чем соответствующие статически определимые, так как имеют дополнительные связи.
2. В статически неопределимых системах возникают меньшие внутренние усилия, что определяет их экономичность по сравнению со статически определимыми системами при одинаковых внешних нагрузках.
3. Нарушение лишних связей в статически неопределимой системе не всегда приводит к разрушению, в то время как потеря связи в статически определимой системе делает ее геометрически изменяемой.
4. Для расчета статически неопределимых систем необходимо предварительно задаваться геометрическими характеристиками поперечных сечений элементов, т.е. фактически их формой и размерами, так как их изменение приводит к изменению усилий в связях и новому распределению усилий во всех элементах системы.
5. При расчете статически неопределимых систем необходимо заранее выбрать материал конструкции, так как необходимо знать его модули упругости.
6. В статически неопределимых системах температурное воздействие, осадка опор, неточности изготовления и монтажа вызывают появление дополнительных усилий.

Основными методами расчетастатически неопределимых систем являются:

1. Метод сил. Здесь в качестве неизвестных рассматриваются усилия – силы и моменты.
2.Метод перемещений. Неизвестными являются деформационные факторы – углы поворотов и линейные смещения.
3.Смешанный метод. Здесь часть неизвестных представляет собой усилия, а другая часть – перемещения.
4. Комбинированный метод. Используется при расчете симметричных систем на несимметричные нагрузки. Оказывается, что на симметричную составляющую заданной нагрузки систему целесообразно рассчитывать методом перемещений, а на обратносимметричную составляющую – методом сил.
Помимо указанных аналитичеких методов при расчете особо сложных систем используются различные численные методы.

Видео:Канонические уравнения метода силСкачать

Канонические уравнения метода сил

Для получения дополнительных уравнений, о которых говорилось в предыдущем параграфе, нужно прежде всего превратить заданную, n раз статически неопределимую систему, в статически определимую, удалив из нее лишние связи. Полученная статически определимая система называется основной. Отметим, что преобразование заданной системы в статически определимую не является обязательным. Иногда используется модификация метода сил, в которой основная система может быть статически неопределимой, однако изложение этого вопроса выходит за рамки этого пособия. Устранение каких-либо связей не изменяет внутренние усилия и деформации системы, если к ней приложить дополнительные силы и моменты, представляющие собой реакции отброшенных связей. Значит, если к основной системе приложить заданную нагрузку и реакции удаленных связей, то основная и заданная системы станут эквивалентными.

В заданной системе по направлениям имеющихся жестких связей, в том числе и тех связей, которые отброшены при переходе к основной системе, перемещений быть не может, поэтому и в основной системе перемещения по направлениям отброшенных связей должны равняться нулю. А для этого реакции отброшенных связей должны иметь строго определенные значения.

Условие равенства нулю перемещения по направлению любой i-ой связи из n отброшенных на основании принципа независимости действия сил имеет вид:

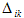
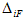
где первый индекс означает направление перемещения и номер отброшенной связи, а второй указывает на причину, вызвавшую перемещение, т.е. — это перемещение по направлению i-ой связи, вызванное реакцией k-ой связи; — перемещение по направлению i-ой связи, вызванное одновременным действием всей внешней нагрузки.

В методе сил реакцию k-ой связи принято обозначать через Xk. С учетом этого обозначения и в силу справедливости закона Гука перемещения 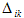можно представить в виде:

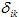
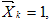
где — единичное (или удельное) перемещение по направлению i-ой связи, вызванное реакцией т.е. реакцией, совпадающей по направлению с Xk, но равной единице.

Подставляя (2) в (1), получим:

Физический смысл уравнения (3): перемещение в основной системе по направлению i-ой отброшенной связи равно нулю.

Записывая выражения, аналогичные (3), для всей совокупности отброшенных связей, получим систему канонических уравнений метода сил:

Вид уравнения (4), т.е. количество слагаемых в каждом из них и их общее число, определяется только степенью статической неопределимости системы и не зависит от ее конкретных особенностей.

Коэффициенты системы канонических уравнений (4) определяются методом Мора-Верещагина путем перемножения соответствующих эпюр. Все эти коэффициенты, как указывалось выше, представляют собой перемещения; коэффициенты, стоящие при неизвестных – единичные перемещения, а свободные члены – грузовые. 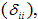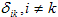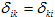Единичные перемещения делятся на главные, расположенные по главной диагонали и имеющие одинаковые индексы и побочные (). Главные перемещения всегда положительные, в отличие от побочных. Симметрично расположенные перемещения в соответствии с теоремой о взаимности перемещений равны друг другу, т.е. .

Видео:25. Статически неопределимая балка. Метод сил ( практический курс по сопромату )Скачать

Алгоритм расчета методом сил

Независимо от особенностей рассматриваемой конструкции, можно выделить следующую последовательность расчета статически неопределимых систем методом сил:

1. Определить степень статической неопределимости.
2. Выбрать основную систему.
3. Сформировать эквивалентную систему.
4. Записать систему канонических уравнений.
5. Построить единичные и грузовые эпюры внутренних силовых факторов, возникающих в элементах рассматриваемой конструкции.
6. Вычислить коэффициенты при неизвестных и свободные члены системы канонических уравнений.
7. Построить суммарную единичную эпюру.
8. Выполнить универсальную проверку коэффициентов при неизвестных и свободных членов.
9. Решить систему (4), т.е. определить реакции лишних связей.
10. Построить эпюры возникающих внутренних силовых факторов для заданной системы (иначе говоря, окончательные эпюры).
11. Выполнить статическую и кинематическую проверки.
Отметим, что пункты 7, 8, 11 приведенного алгоритма не являются безусловно необходимыми, хотя и позволяют контролировать правильность выполнения расчета. А для систем с одной лишней связью пункты 7 и 8 просто лишены смысла, так как в этом случае суммарная единичная эпюра совпадает с единичной.
Остановимся подробнее на некоторых из вышеперечисленных этапов расчета.

Видео:Задача 4. Статически неопределимые рамыСкачать

Выбор основной системы

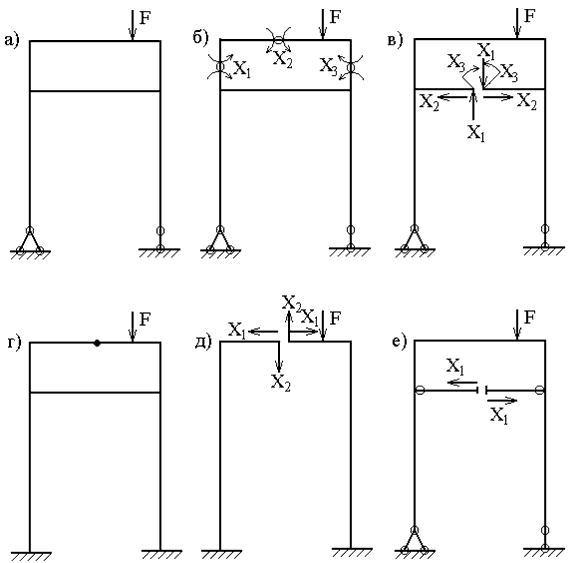
Это важнейший этап расчета, так как рациональный выбор основной системы существенно упрощает вычислительную работу. Рассмотрим возможные способы удаления лишних связей, что и определяет вид основной системы.

1. Отбрасывание лишних связей осуществляется полным удалением некоторых опор или их заменой опорами с меньшим числом связей. Реакции, действующие в направлениях отброшенных связей, являются лишними неизвестными. На рис.1,б, в, г показаны различные варианты эквивалентной системы, полученные этим способом для рамы (рис.1,а).

2.Постановка шарниров в промежуточных сечениях стержней позволяет в каждом таком сечении установить связь, соответствующую изгибающему моменту. Эти моменты являются лишними неизвестными. Для рамы, имеющей степень статической неопределимости n=3 (рис.2,а), при выборе основной системы необходимо поставить три шарнира. Положение этих шарниров может быть произвольным, но удовлетворяющим требованию геометрической неизменяемости системы (рис.2,б).

3. Рассечение стержня устраняет три связи, соответствующие внутренним усилиям M, Q, N (рис.2,в). В частных случаях (рис.2,г) рассечение стержня по шарниру освобождает две связи (рис.2,д), а рассечение прямолинейного стержня с шарнирами по концам – одну связь (рис.2,е).

Среди связей статически неопределимой системы различают абсолютно необходимые и условно необходимые. К абсолютно необходимым относятся связи, при удалении которых система становится геометрически изменяемой. Для абсолютно необходимой связи характерна статическая определимость усилия в ней, т.е. реакция такой связи может быть вычислена из условия равновесия. При выборе основной системы абсолютно необходимые связи отбрасывать нельзя.

Связи, при удалении которых система продолжает оставаться геометрически неизменяемой, называются условно необходимыми. Система, у которой удалили такую связь, может являться основной системой метода сил.

Видео:Метод сил. Пример решения задачи методом сил. Статически неопределимые рамыСкачать

Вычисление коэффициентов и свободных членов канонических уравнений

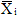
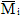
Этому этапу расчета предшествует построение единичных и грузовых эпюр внутренних силовых факторов (для балок и рам – эпюр изгибающих моментов). Единичные эпюры строятся от действия безразмерной единичной силы или безразмерного единичного момента, совпадающих по направлению с направлением соответствующей лишней неизвестной в эквивалентной системе, и обозначаются через , а единичная эпюра – через .

Грузовая эпюра строится от внешней нагрузки, приложенной к основной системе. При этом можно строить одну эпюру от одновременного действия всех внешних нагрузок или несколько эпюр, отдельно от каждой из приложенных нагрузок. Такое разбиение одной грузовой эпюры на несколько более простых, как правило, целесообразно только тогда, когда среди действующих нагрузок есть равномерно распределенная, и эпюра моментов на соответствующем участке под ней является знакопеременной. При этом в каждом каноническом уравнении число свободных членов будет равно числу построенных грузовых эпюр.

Единичные и грузовые перемещения (коэффициенты и свободные члены канонических уравнений) в общем случае можно вычислить методом Мора. Для балок и рам это можно сделать при помощи правила Верещагина.

Видео:Расчет рамы методом силСкачать

Универсальная проверка коэффициентов и свободных членов канонических уравнений

Для выполнения универсальной проверки необходимо построить суммарную единичную эпюру 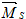— эпюру моментов от одновременного действия всех единичных сил, приложенных к основной системе:

Перемножим суммарную единичную эпюру с эпюрой :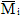

Таким образом результат перемножения суммарной и i-ой единичной эпюр — это перемещение по направлению i-ой связи от совместного действия единичных лишних неизвестных. Это перемещение равно сумме коэффициентов i-го канонического уравнения:

Такая проверка называется построчной и выполняется для каждого канонического уравнения.
Вместо n построчных проверок чаще всего выполняется одна – универсальная поверка, которая состоит в перемножении суммарной единичной эпюры самой на себя и проверке условия:

Если универсальная проверка выполняется, значит единичные перемещения вычислены правильно; если нет – необходимо выполнить построчные проверки, что позволит уточнить перемещение, при вычислении которого допущена ошибка.

Для выполнения проверки грузовых перемещений необходимо перемножить суммарную единичную и грузовую эпюры изгибающих моментов:

Таким образом, проверка свободных членов системы канонических уравнений (4) состоит в выполнении условия:

Видео:Статически неопределимые системы. Метод силСкачать

Построение окончательных эпюр внутренних силовых факторов

Окончательные эпюры можно построить двумя способами.

Так как при найденных значениях лишних неизвестных Xi выполняются условия совместности деформаций, то из расчета основной системы можно получить все искомые внутренние усилия заданной системы. На основании принципа независимости действия сил для изгибающих моментов получим:

или, учитывая, что

приходим к выражению:

Аналогично определяется продольные и поперечные силы:

Второй способ основан на том, что в результате вычисления реакций лишних связей Xi исходная статически неопределимая система приведена к статически определимой системе, загруженной внешними нагрузками и реакциями лишних связей. Поэтому окончательные эпюры внутренних силовых факторов можно построить для эквивалентной системы, вычислив предварительно (и то не всегда) из условий равновесия опорные реакции последней.

Недостатком первого способа является то обстоятельство, что для его реализации необходимо дополнительно построить эпюры Qi, Ni (i=1, 2, …,n), Qf, Nf, которые не используются в расчете методом сил и поэтому не были построены ранее.

В связи с этим для построения окончательных эпюр более рациональным представляется второй способ, а условие (8) можно использовать в качестве дополнительной проверки.

Видео:Канонические уравнения метода перемещенийСкачать

Проверка окончательной эпюры изгибающих моментов

Эта проверка выполняется в двух вариантах: статическая и кинематическая.

При статической проверке, выполняемой обычно для рам, вырезаются узлы и записываются условия их равновесия под действием узловых сосредоточенных моментов и изгибающих моментов на концах стержней. Эта проверка является вспомогательной и выполняется автоматически при правильных эпюрах изгибающих моментов в основной системе и при выполнении кинематической проверки.

Статическая проверка эпюр Q и N состоит в том, что для любой отсеченной части рамы сумма проекций на две оси всех действующих сил – внешних нагрузок и внутренних усилий – должна быть равна нулю.

Основной проверкой окончательной эпюры моментов в методе сил является кинематическая проверка, которая может быть построчной или универсальной.
При построчной проверке каждая единичная эпюра моментов 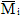перемножается с окончательной эпюрой моментов М:

Таким образом, в результате перемножения каждой единичной эпюры с окончательной эпюрой моментов получим ноль:

Вариантом построчной проверки является проверка по замкнутомуконтуру, состоящая в том, что сумма приведенных (т.е. деленных на жесткость соответствующего стержня или его участка) площадь эпюры М, находящихся внутри каждого замкнутого бесшарнирного контура, должна быть равна сумме приведенных площадей, находящихся снаружи этого контура.

Суммируя выражения типа (11) для всех n, получим выражение, служащее для универсальной кинематической проверки окончательной эпюры изгибающих моментов:

Формулу (12) можно интерпретировать следующим образом: условное перемещение эквивалентной, или, что то же самое, заданной системы по направлению всех неизвестных от действия всех неизвестных и внешних нагрузок, равно нулю.

Видео:Расчёт статически неопределимой рамы по Методу Сил (с одной неизвестной)Скачать

Определение перемещений в статически неопределимых системах

Для определения перемещения в статически неопределимой системе используется тождественность заданной и эквивалентной систем в том смысле, что если условия совместности деформаций выполняются, т.е. справедливы уравнения (4), то перемещения в эквивалентной системе соответствуют перемещениям заданной системы. Тогда, построив для основной системы эпюру изгибающих моментов 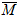от единичной силы (или единичного момента) приложенной в направлении искомого перемещения, величину перемещения находим по формуле:

где М – эпюра изгибающих моментов от внешней нагрузки, построенная для статически неопределимой системы.

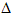
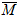
Отметим, что при вычислении перемещения можно поступить и наоборот: единичную эпюру моментов построить в статически неопределимой заданной системе, а эпюру моментов от внешних нагрузок М – в основной (статически определимой) системе.

Пример расчета

Построить эпюры продольных, поперечных сил и изгибающих моментов для плоской рамы (рис.3,а).

Степень статической неопределимости рамы:

n = r — s = 4 — 3 = 1

Выбираем основную систему, отбрасывая на правой опоре горизонтальный стержень (рис.3,б), т.е. заменяем шарнирно-неподвижною опору на шарнирно-подвижную. На базе основной системы формируем эквивалентную систему (рис.3,в).

Заменяя реакцию лишней связи соответствующей единичной силой, (рис. 3,г) строим эпюру моментов M1 (рис.3,д).

Грузовая эпюра моментов 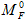(рис.3,ж), построенная от одновременного действия всех внешних нагрузок (рис.3,е), является знакопеременной на участке, где действует нагрузка q. Это создает определенные трудности (хотя и не непреодолимые!) при ее перемножении с единичной эпюрой M1. В связи с этим целесообразно построить две грузовых эпюры – отдельно от нагрузки q (эпюра Mq) и от совместного действия F и M (эпюра MF). Эти варианты нагружения и эпюры представлены на рис.3,з и рис.3,а,б,в.

При таком разбиении внешней нагрузки каноническое уравнение метода сил содержит два грузовых перемещения и имеет вид:

Вычислим коэффициенты канонического уравнения:

Реакция лишних связи:

Эпюры Nz, Qy, Mx для заданной системы, загруженной нагрузками F, M, q и X1 (рис.3,г) представлены на рис.3,д,е,ж.

Как уже говорилось, при построении эпюр Nz и Q в рамах ординаты можно откладывать в любую сторону, но обязательно указывать знаки; а при построении эпюр Mx знаки можно не указывать, но обязательно откладывать ординаты со стороны сжатых волокон соответствующих элементов.

В рассмотренном примере универсальная проверка правильности вычисления коэффициентов канонического уравнения и свободных членов не выполнялась, так как рама имеет степень статической неопределимости n = 1, а, значит, суммарная единичная эпюра (если ее построить) совпадет с единичной эпюрой M1. В этом случае можно (и желательно!) проверить правильность выполнения расчета при помощи универсальной кинематической проверки окончательной эпюры моментов Mx.

Выполним эту проверку для рамы, рассмотренной в последнем примере (рис.3,а). Должно выполняться условие:

Покажем отдельно фрагменты перемножаемых эпюр (рис.3,д и рис.4,ж) для ригеля (рис.5,а,б) и стойки (рис.5,в,г) с указанением всех характерных размеров и соответствующих им ординат. Причем стойка (на рис.5,в,г) показана в горизонтальном положении.

Точка пересечения кривой на ригеле эпюры Mx с осью (рис.5,б) определяется следующим образом. Обозначим координату произвольного сечения, отсчитываемую от правого конца ригеля, через z, тогда момент Mx определяется в виде: