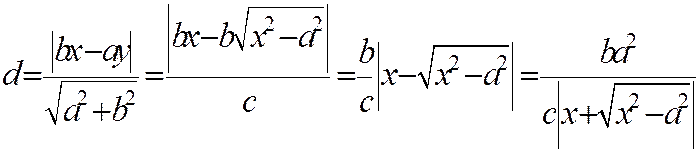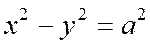Каноническое уравнение гиперболы исследование ее формы асимптоты (7 видео)

Содержание

Исследование формы гиперболы
Исследование формы гиперболы по ее каноническому уравнению. Уравнение асимптот гиперболы
68. Исследование гиперболы по каноническому уравнению. Асимптоты гиперболы по каноническому уравнению. Равносторонняя гипербола. Эксцентриситет гипербол
📹 Видео

Видео:Видеоурок "Гипербола"Скачать

Исследование формы гиперболы

Так как в каноническое уравнение гиперболы координаты х и у входят во второй степени. То оси Ох и Оу являются осями симметрии гиперболы, заданной уравнением: 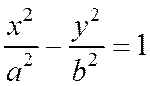. (1)

а начало координат – центром симметрии.

Из уравнения (1) следует, что

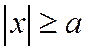
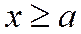
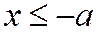
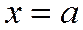
т.е. или , или . Геометрически это означает, что между прямыми и нет ни одной точки гиперболы (1).

Ось симметрии Оу не пересекает гиперболу, заданную уравнением (1), и называется мнимой осью. Ось Ох – пересекает гиперболу (1) в двух точках:

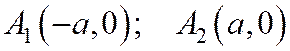
Эта ось называется действительной осью гиперболы. Точки, в которых действительная ось пересекается гиперболу, называются вершинами гиперболы.

Числа а и b в каноническом уравнении называются действительной и мнимой полуосями гиперболы.

Решая уравнение (1) относительно у, беря лишь положительное значение: 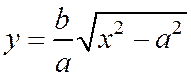(2)

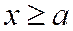
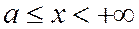
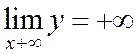
и считая , мы получим точки гиперболы (1), лежащие в первой четверти. Из уравнения (2) следует, что у в полуинтервале есть возрастающая функция; при этом

Всякая прямая пересекает гиперболу не более чем в двух точках, так как прямая определяется уравнением первой степени, а гипербола – второй.

Рассмотрим уравнение прямой (3)

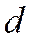
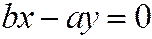
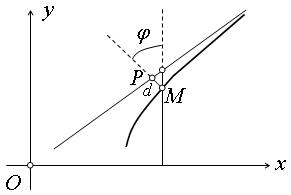
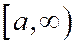
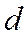
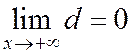
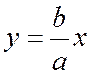
Найдем расстояние от точки М(х, у), лежащей на дуге гиперболы, определяемой уравнением (2), до прямой (3); переписывая уравнение (3) в виде , находим:

Отсюда следует, то на полуинтервале расстояние от точки М(х, у) рассматриваемой части гиперболы до прямой (3) есть убывающая функция от х и (рис. 167). Прямая, определяемая уравнением называется асимптотой гиперболы.

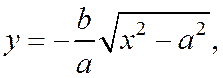
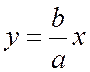
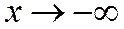
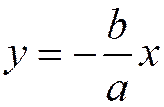
В силу того, что гипербола, заданная каноническим уравнением, симметрична относительно начала координат, расстояние от точки М(х, у), лежащей на дуге гиперболы, заданной уравнением до прямой стремиться к нулю при . Так как гипербола, заданная каноническим уравнением, симметрична и относительно оси Оу, то она имеет вторую асимптоту ,

которая обладает свойством, аналогичным свойству первой асимптоты по отношению к дугам гиперболы, расположенным во второй и четвертой четвертях.

Асимптоты гиперболы являются диагоналями прямоугольника , , , .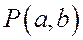

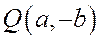
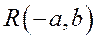
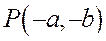
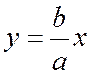
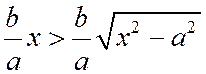
При одной и той же абсциссе х ординаты точки ветви гиперболы, лежащей в первой четверти, с ординатой точки асимптоты связаны неравенством: .

Отсюда и из того, что гипербола симметрична относительно осей координат, следует, что она имеет две ветви, заключенные в двух областях: одна из них ограничена отрезком и продолжениями отрезков и за точки и , другая симметрична этой области относительно мнимой оси гиперболы (рис 168).

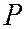
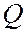
Рис.168

Гипербола, у которой полуоси равны, называются равносторонней. Каноническое уравнение равносторонней гиперболы имеет вид

Уравнение асимптот равносторонней гиперболы таковы:

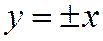
это биссектрисы углов между ее осями симметрии. Асимптоты равносторонней гиперболы взаимно перпендикулярны.

Обратно, если асимптоты гиперболы взаимно перпендикулярны, то ее полуоси равны между собой и, значит гипербола равносторонняя.

Видео:Математика без Ху!ни. Нахождение асимптот, построение графика функции.Скачать

Исследование формы гиперболы по ее каноническому уравнению. Уравнение асимптот гиперболы

Общее уравнение кривых второго порядка

Кривыми второго порядка называются фигуры, множество точек которых расположено в плоскости двумерной системы координат.

Общее уравнение кривой второго порядка:

Ax 2 +By 2 +2Cxy+Dx+Ey+F=0

Где A 2 +B 2 +C 2 ≠0

К кривым второго порядка относятся:

Определение и вывод канонического уравнения окружности.

Окружностью называется множество точек плоскости, удаленных на одно и то же расстояние, называемое радиусом, от фиксированной точки, называемой центром окружности.

Вывод канонического уравнения:

Пусть введена система координат и центр с координатами C (a, b). Тогда точка M (x, y) принадлежит окружности, если расстояние от центра до M будет равно радиусу: CM=R

(x-a) 2 +(y-b) 2 = R 2

Это уравнение и называют каноническим уравнением окружности.

Определение и вывод канонического уравнения эллипса.

Эллипсом называют множество точек плоскости, для каждой из которых сумма расстояний до двух фиксированных точек, называемых фокусами, есть величина постоянная и большая, чем расстояние между фокусами.

Выведем каноническое уравнение эллипса.

Таким оно будет в специально выбранной системе координат на плоскости: проведем прямую через фокусы F1 и F2 и направим её оси от первого ко второму, возьмем середину F1F2, обозначим её за О и поместим в О начало системы координат. Так определяется ось Ох. Повернем ось Ох относительно О на 90˚ против часовой стрелки и тем самым образуем ось Оy. Фокусы имеют координаты: F1 (-c, 0), F2 (c, 0).

√((x+c) 2 +y 2 ) + √ ((x-c) 2 +y 2 ) = 2a

√((x+c) 2 +y 2 )= 2a-√ ((x-c) 2 +y 2 )

x 2 +2xc+c 2 +y 2 =4a 2 -4a√ ((x-c) 2 +y 2 )+ x 2 -2xc+c 2 +y 2

4cx-4a 2 =-4a√ ((x-c) 2 +y 2 )

a 2 -cx =a√ ((x-c) 2 +y 2 )

a 4 -2a 2 cx+c 2 x 2 =a 2 ((x-c) 2 +y 2 )

a 4 -2a 2 cx+c 2 x 2 =a 2 x 2 -2a 2 cx+a 2 c 2 +a 2 y 2

a 4 -a 2 c 2 =(a 2 -c 2 )x 2 +a 2 y 2

(a 2 -c 2 )x 2 +a 2 y 2 =a 2 (a 2 -c 2 )

b 2 x 2 +a 2 y 2 =a 2 b 2 :a 2 b 2

x 2 /a 2 +y 2 /b 2 =1 – каноническое уравнение эллипса

Исследование формы эллипса по его каноническому уравнению. Параметры эллипса; связь между ними.

y 2 =b 2 (1-x 2 /a 2 )

y 2 =b 2 /a 2 (a 2 -x 2 )

Эллипс находится внутри прямоугольника со сторонами а, b.

Если точка М0 (х0, у0) принадлежит эллипсу, то и точки М1 (-х0, у0), М2 (х0, -у0), М3 (-х0, -у0) принадлежат этому эллипсу. Это значит что эллипс имеет две оси симметрии – Ох и Оу, и центр симметрии – точку О. Заметим, что точки (а, 0) и (0, b) находятся на осях симметрии и принадлежат эллипсу. Эти точки пересечения эллипса с осями симметрии называются вершинами. Числа a и b называют полуосями эллипса, а 2a и 2b – осями эллипса.

Эксцентриситет эллипса. Оптическое свойство эллипса

Эксцентриситетом эллипса называют отношение расстояния между фокусами к большей оси.

E=√((a 2 -b 2 )/a 2 )= √(1-b 2 /a 2 )

Если Е=0, то это означает, что b=a, с=0, уравнение эллипса x 2 +y 2 =a 2 – окружность с центром в начале координат и радиусом а. Иначе говоря, окружность – это эллипс с Е=0.

Если Е=1, то с=а, b=0, тогда эллипс становится отрезком [-a, a].

Если зафиксировать а, то смысл эксцентриситета становиться таким: чем больше эксцентриситет, тем больше вытянут эллипс вдоль оси Ох.

Оптическое свойство эллипса.

Предположим, что изнутри эллипс покрыт зеркальным веществом. Пусть из одного фокуса посылают световой луч. Отражаясь от касательной к эллипсу в точке падения луча, он попадает во второй фокус эллипса.

Параметрические уравнения окружности и эллипса.

Возьмем окружность: x 2 +y 2 =R 2

Параметрическое уравнение окружности

Если t принадлежит [0,2П], то точка М(х, у) принадлежит окружности.

Параметрическое уравнение эллипса:

x 2 /a 2 +b 2 sin 2 (t)/b 2 =0

x=a*cos(t), т.к знак cos(t) и знак x во всех четвертях совпадают.

7. Связь между параметрами эллипса в случае b>a.

Если a 2 =a 2 +c 2 , c 2 =b 2 -a 2

Эллипс вытянут вдоль оси Оу.

Определение и вывод канонического уравнения гиперболы

Гиперболой называется множество точек плоскости, для каждой из которых модуль разности расстояний до двух фиксированных точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.

Для вывода канонического уравнения гиперболы используется такая же система координат, как и для эллипса. (см билет №3)

√((x+c) 2 +y 2 )- √((x-c) 2 +y 2 )=±2a

(√((x+c) 2 +y 2 )) 2 =(√((x-c) 2 +y 2 ) ±2a) 2

x 2 +2xc+c 2 +y 2 =x 2 -2xc+c 2 +y 2 ±4a√((x-c) 2 +y 2 )+4a 2

4cx-4a 2 =±4a√((x-c) 2 +y 2 )

c 2 x 2 -2cxa 2 +a 4 =a 2 (x 2 -2cx+c 2 +y 2 )

c 2 x 2 +a 4 =a 2 x 2 +a 2 c 2 +a 2 y 2

(c 2 -a 2 )x 2 -a 2 y 2 =a 2 (c 2 -a 2 )

c 2 -a 2 >0 т.к. c>a

b 2 x 2 -a 2 y 2 =a 2 b 2 : a 2 b 2

x 2 /a 2 -y 2 /b 2 =1 – каноническое уравнение гиперболы

Исследование формы гиперболы по ее каноническому уравнению. Уравнение асимптот гиперболы

Т.к уравнение содержит только x 2 и y 2 , то, как и в случае эллипса, доказывается, что гипербола имеет две оси симметрии (Ох и Оу) и центр симметрии в точке О.

Выразим из уравнения у.

x 2 /a 2 -1=y 2 /b 2

y 2 =b 2 x 2 /a 2 -b 2

x≠0 ни при каких y

F (±c, 0) – фокусы гиперболы.

График гиперболы в первой четверти: y=b/a*√(x 2 -a 2 )

Найдем асимптоту гиперболы:

h= lim_(x=>+∞) (b/a√(x 2 -a 2 )-b/a*x)=b/a lim_(x=>+∞) (√(x 2 -a 2 )-x) = b/a lim_(x=>+∞) ((x 2 -a 2 -x 2 )/( √ (x 2 -a 2 )+x)=b/a * -a 2 /∞=0

Прямая y=b/a *x является асимптотой гиперболы в первой и третьей четверти. Очевидно, что прямая y=-b/a *x является асимптотой во второй и четвертой координатных четвертях.

Числа а и b называют вещественной и мнимой полуосями соответственно. Числа 2а и 2b – вещественной и мнимой осями.

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

68. Исследование гиперболы по каноническому уравнению. Асимптоты гиперболы по каноническому уравнению. Равносторонняя гипербола. Эксцентриситет гипербол

В § 3 доказано, что в канонической системе координат OXy Уравнение гиперболы имеет вид:

. (1)

1. Гипербола не проходит через начало системы координат, так как координаты точки О(0,0) не удовлетворяют уравнению (1).

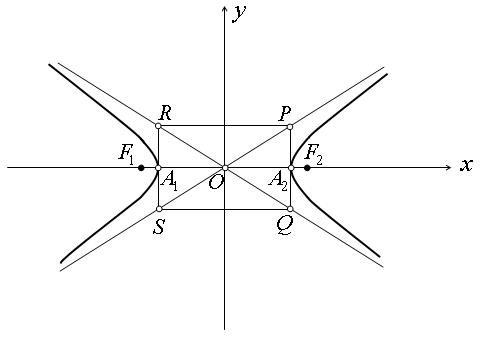
2. Найдем точки пересечения гиперболы с осями координат. Для нахождения точки пересечения с осью ОХ полагаем в уравнении (1) У = 0 и находим X = ±A. Таким образом гипербола пересекает ось ОХ В точках A1(-A, 0), A2(A, 0). Так как уравнение (3) не имеет решений при У = 0, то гипербола не пересекает ось ОY.

Точки A1, A2 называются Действительными вершинами гиперболы, Отрезок A1A2, B1B2 Действительной осью гиперболы; |A1A2| =2A; A называются действительной полуосью гиперболы. Точки B1(0,-B), B2(0, B) называются Мнимыми вершинами гиперболы, Отрезок B1B2 Мнимой осью гиперболы; |B1B2| =2B; B называются мнимой полуосью гиперболы.

3. Так как все переменные входят в уравнение (1) в четной степени, то вместе с точкой (X, Y) гиперболе принадлежат четыре точки (±X, ±Y) (с произвольными комбинациями знаков). Таким образом, гипербола симметрична относительно, всех координатных осей OX, OY и начала координат. Точка О называется Центром Гиперболы.