- Немного теории
- Приведение к каноническому виду
- Решение ДУ в ЧП
- Разные задачи на исследование ДУ в ЧП
- Помощь с решением ДУ в ЧП
- Приведение к каноническому виду линейных уравнений с частными производными второго порядка
- Система линейных уравнений с тремя переменными
- Линейное уравнение с тремя переменными и его решение
- Решение системы линейных уравнений с тремя переменными методом подстановки
- Решение системы линейных уравнений с тремя переменными методом Крамера
- Примеры
- 🌟 Видео
Видео:Приведение ДУ 2 порядка в частных производных к каноническому видуСкачать
Немного теории
Дифференциальным уравнением с частными производными (ДУ с ЧП) называется уравнение относительно неизвестной функции нескольких переменных (ФНП) и ее частных производных. Наивысший порядок частных производных (существенно входящих в уравнение) называется порядком этого уравнения.
ДУ с ЧП называется линейным (ЛДУ с ЧП), если неизвестная функция и ее производные входят в это ДУ линейно (в первой степени).
В этом разделе вы найдете подробно решенные задачи по темам: классификация и приведение к каноническому виду ДУ с ЧП второго порядка с двумя переменными, определение типа уравнения, решение уравнений и систем ДУ в ЧП.
ДУ с ЧП находят широкое применение в прикладных науках: квантовая механика, электродинамика, термодинамика, теория теплои массопереноса и др. при математическом описании и моделировании различных физических процессов. Поэтому такие уравнения изучаются под общим названием уравнений математической физики (примеры решений 16 задач).
Видео:Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать
Приведение к каноническому виду
Задача 1. Привести к каноническому виду уравнение
Задача 2. Привести уравнение к каноническому виду.
Задача 3. Найти общее решение уравнения, приведя его к каноническому виду:
Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать
Решение ДУ в ЧП
Задача 4. Решить уравнение Пфаффа
$$ z^2 dx +zdy +(3zx +2y)dz=0. $$
Задача 5. Решить задачу Коши для уравнения в частных производных
$$ u_-2Delta u =(x^2+y^2+z^2)t; quad u(t=0)=xyz, u_t(t=0)=x-y. $$
Задача 6. Найти общее решение уравнения в частных производных
Задача 7. Найти общее решение уравнения в частных производных первого порядка.
$$ xy u_x +(x-2u)u_y = yu. $$
Задача 8. Найти решение задачи Коши для уравнения в частных производных
$$ y u_x -xy u_y=2xu, quad u(x+y=2)=1/y. $$
Задача 9. Решить систему дифференциальных уравнений в частных производных
Видео:Приведение линейного уравнения в частных производных c постоянными коэфф--ми к каноническому виду.Скачать
Разные задачи на исследование ДУ в ЧП
Задача 10. Найти поверхность, удовлетворяющую данному уравнению и проходящую через данную линию
Задача 11. Найти области гиперболичности, эллиптичности и параболичности уравнения и исследовать их зависимость от $l$, где $l$ – числовой параметр.
Задача 12. Найти функцию, гармоническую внутри круга радиуса $R$ c центром в начале координат и такую, что
Видео:13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать
Помощь с решением ДУ в ЧП
Если вам нужна помощь с решением задач и контрольных по дифференциальным уравнениям (и другим разделам математического анализа), обращайтесь в МатБюро. Стоимость подробной консультации от 100 рублей , оформление производится в Word, срок от 1 дня.
Видео:Написать канонические и параметрические уравнения прямой в пространствеСкачать
Приведение к каноническому виду линейных уравнений с частными производными второго порядка
Федеральное агентство по образованию
ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Институт математики, экономики и информатики
Кафедра дифференциальных и интегральных уравнений
ПРИВЕДЕНИЕ К КАНОНИЧЕСКОМУ ВИДУ ЛИНЕЙНЫХ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ВТОРОГО ПОРЯДКА
Приведение к каноническому виду линейных уравнений с частными производными 2-го порядка с двумя независимыми переменными …………………………………………………………………………
1.1. Необходимый теоретический материал………………………..
1.2. Пример выполнения задачи1 (приведение к
каноническому виду уравнений гиперболического типа) .
1.3. Пример выполнения задачи 2 (приведение к
каноническому виду уравнений параболического типа)
1.4. Пример выполнения задачи 3 (приведение к
каноническому виду уравнений эллиптического типа) ..
1.5. Задачи для самостоятельного решения ………………….….
Упрощение группы младших производных
для уравнений второго порядка с постоянными коэффициентами
2.1. Необходимый теоретический материал …………………..
2.2. Пример выполнения задачи 4
2.3. Задачи для самостоятельного решения ……………………..
В настоящих методических указаниях изложен теоретический материал и на конкретных примерах разобрано приведение к каноническому виду линейных уравнений с частными производными второго порядка с двумя независимыми переменными для уравнений гиперболического, эллиптического и параболического типов.
Методические указания предназначены для студентов математических специальностей очной и заочной формы обучения.
§1. Приведение к каноническому виду линейных уравнений с частными производными 2-го порядка с двумя независимыми переменными.
Задача. Определить тип уравнения
(1)
и привести его к каноническому виду.
1.1. Необходимый теоретический материал.
I. Тип уравнения (1) определяется знаком выражения 
:
· если 
в некоторой точке, то уравнение (1) называется уравнением гиперболического типа в этой точке;
· если 
в некоторой точке, то уравнение (1) называется уравнением эллиптического типа в этой точке;
· если 
в некоторой точке, то уравнение (1) называется уравнением параболического типа в этой точке.
Уравнение (1) будет являться уравнением гиперболического, эллиптического, параболического типа в области D, если оно гиперболично, эллиптично, параболично в каждой точке этой области.
Уравнение (1) может менять свой тип при переходе из одной точки (области) в другую. Например, уравнение 
является уравнением эллиптического типа в точках 
; параболического типа в точках 
; и гиперболического типа в точках 
.
II. Чтобы привести уравнение к канонического виду, необходимо:
1. Определить коэффициенты 
;
2. Вычислить выражение ;
3. Сделать вывод о типе уравнения (1) (в зависимости от знака выражения );
4. Записать уравнение характеристик:
; (2)
5. Решить уравнение (2). Для этого:
а) разрешить уравнение (2) как квадратное уравнение относительно dy:
; (3)
б) найти общие интегралы уравнений (3) (характеристики уравнения (1)):
· 
(4)
в случае уравнения гиперболического типа;
· 
, (5)
в случае уравнения параболического типа;
· 
, (6)
в случае уравнения эллиптического типа.
6. Ввести новые (характеристические) переменные 
и 
:
· в случае уравнения гиперболического типа в качестве и берут общие интегралы (4) уравнений (3), т. е.
· в случае уравнения параболического типа в качестве берут общий интеграл (5) уравнения (3), т. е. 
, в качестве берут произвольную, дважды дифференцируемую функцию 
, не выражающуюся через 
, т. е. 
;
· в случае уравнения эллиптического типа в качестве и берут вещественную и мнимую часть любого из общих интегралов (6) уравнений (3):
7. Пересчитать все производные, входящие в уравнение (1), используя правило дифференцирования сложной функции:
,
,
, (7)
,
.
8. Подставить найденные производные в исходное уравнение (1) и привести подобные слагаемые. В результате уравнение (1) примет один из следующих видов:
· в случае уравнения гиперболического типа:
;
· в случае уравнения параболического типа:
;
· в случае уравнения эллиптического типа:
.
1.2. Пример выполнения задачи 1.
Определить тип уравнения
и привести его к каноническому виду.
1. Определим коэффициенты :
2. Вычислим выражение :
.
3. 
уравнение гиперболического типа во всей плоскости XOY.
4. Запишем уравнение характеристик:
. (9)
5. Решим уравнение (9). Для этого:
а) разрешаем уравнение (9) как квадратное уравнение относительно dy: 
;
;
(10)
б) найдём общие интегралы уравнений (10) (характеристики уравнения (9)):
6. Введём характеристические переменные:
7. Пересчитаем производные, входящие в исходное уравнение.
Используя формулы (7), получим:
Здесь слева написаны коэффициенты уравнения (8) при соответствующих производных.
8. Собирая подобные слагаемые, получим:
Или после деления на -100 (коэффициент при 
):
Ответ. Уравнение (8) является уравнением гиперболического типа на всей плоскости XOY. Канонический вид
где 
1.3. Пример выполнения задачи 2.
Определить тип уравнения
и привести его к каноническому виду.
1. Определим коэффициенты . В нашем примере они постоянны:
2. Вычислим выражение :
.
3. 
уравнение параболического типа во всей плоскости XOY.
4. Запишем уравнение характеристик:
. (12)
5. Решим уравнение (12). Для этого:
а) разрешаем уравнение (9) как квадратное уравнение относительно dy. Однако в этом случае левая часть уравнения является полным квадратом:
;
(13)
б) имеем только одно уравнение характеристик (13). Найдём его общий интеграл (уравнения параболического типа имеют только одно семейство вещественных характеристик):
6. Введём характеристические переменные: одну из переменных 
вводим как и ранее
а в качестве берут произвольную, дважды дифференцируемую функцию, не выражающуюся через , пусть
;
7. Пересчитаем производные, входящие в исходное уравнение.
Используя формулы (7), получим:
Здесь слева написаны коэффициенты уравнения (11) при соответствующих производных.
8. Собирая подобные слагаемые, получим:
Функцию, стоящую в правой части уравнения (11) необходимо также выразить через характеристические переменные.
После деления на 25 (коэффициент при 
):
Ответ. Уравнение (11) является уравнением параболического типа на всей плоскости XOY. Канонический вид
где 
1.4. Пример выполнения задачи 3.
Определить тип уравнения
(14)
и привести его к каноническому виду.
1. Определим коэффициенты :
2. Вычислим выражение :
.
3. 
уравнение эллиптического типа во всей плоскости XOY.
4. Запишем уравнение характеристик:
. (15)
5. Решим уравнение (15). Для этого:
а) разрешаем уравнение (15) как квадратное уравнение относительно dy: 
; (16)
б) уравнения (16) – это пара комплексно-сопряженных уравнений. Они имеют пару комплексно-сопряженных общих интегралов. (Уравнения эллиптического типа не имеют вещественных характеристик)
(17)
6. Введём характеристические переменные как вещественную и мнимую части одного из общих интегралов (17):
7. Пересчитаем производные, входящие в исходное уравнение.
Используя формулы (7), получим:
Здесь слева написаны коэффициенты уравнения (14) при соответствующих производных.
8. Собирая подобные слагаемые, получим:
Или после деления на 4 (коэффициент при 
и 
):
Ответ. Уравнение (14) является уравнением эллиптического типа на всей плоскости XOY. Канонический вид
где 
1.5. Задачи для самостоятельного решения.
Определить тип уравнения и привести его к каноническому виду.
.
.
.
.
.
.
.
.
.
.
Определить тип уравнения и привести его к каноническому виду.
Определить тип уравнения и привести его к каноническому виду.
§2. Упрощение группы младших производных
для уравнений второго порядка с постоянными коэффициентами
2. 1. Необходимый теоретический материал
В самом общем виде линейное уравнение с частными производными второго порядка с двумя независимыми переменными имеет вид
(1)
Преобразованием независимых переменных группа старших производных уравнения может быть упрощена. Уравнение (1) приводится к одному из следующих видов
· в случае уравнения гиперболического типа:
; (11)
· в случае уравнения параболического типа:
; (12)
· в случае уравнения эллиптического типа:
. (13)
Если коэффициенты исходного уравнения постоянны, то для дальнейшего упрощения уравнения любого типа нужно сделать замену неизвестной функции
, (14)
где 
- новая неизвестная функция, 
- параметры, подлежащие определению. Такая замена не «испортит» канонического вида, но при этом позволит подобрать параметры так, чтобы из трех слагаемых группы младших производных в уравнении осталось только одно. Уравнения гиперболического, параболического и эллиптического типов соответственно примут вид
;
;
.
Чтобы реализовать замену (14) в уравнениях (11), (12), (13), необходимо пересчитать все производные, входящие в эти уравнения по формулам
(15)
Подробно рассмотрим этот процесс на примере уравнения гиперболического типа, т. е. уравнения (11). Пересчитаем производные, входящие в это уравнение, используя формулы (15).
Здесь слева расставлены соответствующие коэффициенты уравнения (11). Собирая подобные слагаемые, получим
. (16)
В уравнении (16) приравняем к нулю коэффициенты при 
и 
Откуда 
Подставив эти значения параметров в уравнение (16) и разделив его на 
, придем к уравнению
,
где 
.
2.2. Пример выполнения задачи 4
к каноническому виду и упростить группу младших производных.
9. Определим коэффициенты :
10. Вычислим выражение :
.
11. 
уравнение эллиптического типа во всей плоскости XOY.
12. Запишем уравнение характеристик:
. (18)
5. Решим уравнение (18). Для этого:
а) разрешаем уравнение (18) как квадратное уравнение относительно dy: 
;
; (19)
б) найдём общие интегралы уравнений (19) (характеристики уравнения (17)):
6. Введём характеристические переменные:
13. Пересчитаем производные, входящие в исходное уравнение.
Используя формулы (7), получим:
Здесь слева написаны коэффициенты уравнения (17) при соответствующих производных.
14. Собирая подобные слагаемые, получим:
(20)
Теперь с помощью замены неизвестной функции (14)
упростим группу младших производных.
Пересчитаем производные, входящие в уравнение (20), используя формулы (15).
Здесь слева расставлены соответствующие коэффициенты уравнения (20). Собирая подобные слагаемые, получим
. (21)
В уравнении (21) приравняем к нулю коэффициенты при и
Откуда 
Подставив эти значения параметров в уравнение (21) и разделив его на , придем к уравнению
.
Ответ. Уравнение (20) является уравнением эллиптического типа на всей плоскости XOY. Его канонический вид
,
где 
.
2.3. Задачи для самостоятельного решения
Задача 4. Привести уравнения к каноническому виду и упростить группу младших производных.
.
.
.
.
.
.
.
.
.
.
Видео:Видеоурок "Канонические уравнения прямой"Скачать
Система линейных уравнений с тремя переменными
Линейное уравнение с тремя переменными и его решение
Уравнение вида ax+by+cz = d , где a, b, c, d - данные числа, называется линейным уравнением с тремя переменными x, y и z.
Например: $2x+5y+z = 8; -x+1, 5y+2z = 0; frac x-8y-5z = 7$
Уравнение с тремя переменными может быть не только линейным, т.е. содержать не только первые степени переменных x,y и z.
Например: $2x^2+xz+y^2+yz^2 = 3,x-5y^2+z^3 = 1, 7x^3+y+xyz = 7$
Решением уравнения с тремя переменными называется упорядоченная тройка значений переменных (x,y,z), обращающая это уравнение в тождество.
О тождествах – см. §3 данного справочника
Например: для уравнения 2x+5y+z=8 решениями являются тройки x = -2, y = 1, z = 7; x = -1, y = 1, 6 , z = 2; x = -3, y = 2, 4, z = 2 и т.д. Уравнение имеет бесконечное множество решений.
Геометрическим представлением линейного уравнения с тремя переменными является плоскость в трёхмерном координатном пространстве .
Решение системы линейных уравнений с тремя переменными методом подстановки
Алгоритм метода подстановки для системы уравнений с тремя переменными аналогичен алгоритму для двух переменных (см.§45 данного справочника)
Например: решить систему
$$ <left< begin 3x+2y-z = 8 \ x-y+z = -2 \ 2x-3y-5z = 1 end right.> Rightarrow <left< begin 3(y-z-2)+2y-z = 8 \ x = y-z-2 \ 2(y-z-2)-3y-5z = 1 end right.> Rightarrow $$
$$ Rightarrow <left< begin x = y-z-2 \ 5y-4z = 14 \ -y-7z = 5 end right.> Rightarrow <left< begin x = y-z-2 \ y = -7z-5 \ 5(-7z-5)-4z = 14 end right.> Rightarrow <left< begin x = y-z-2 \ y = -7z-5 \ -39z = 39 end right.> Rightarrow $$
$$ Rightarrow <left< begin x = 2-(-1)-2 = 1 \ y = -7cdot(-1)-5 = 2 \ z = -1 end right.> Rightarrow <left< begin x = 1 \ y = 2 \ z = -1 end right.> $$
Решение системы линейных уравнений с тремя переменными методом Крамера
Для системы с 3-мя переменными действуем по аналогии.
Дана система 3-х линейных уравнений с 3-мя переменными:
$$ <left< begin a_1 x+b_1 y+c_1 z = d_1 \ a_2 x+b_2 y+c_2 z = d_2 \ a_3 x+b_3 y+c_3 z = d_3 end right.> $$
Определим главный определитель системы:
$$ Delta = begin a_1 & b_1 & c_1 \ a_2 & b_2 & c_2 \ a_3 & b_3 & c_3 end $$
и вспомогательные определители :
$$ Delta_x = begin d_1 & b_1 & c_1 \ d_2 & b_2 & c_2 \ d_3 & b_3 & c_3 end, Delta_y = begin a_1 & d_1 & c_1 \ a_2 & d_2 & c_2 \ a_3 & d_3 & c_3 end, Delta_z = begin a_1 & b_1 & d_1 \ a_2 & b_2 & d_2 \ a_3 & b_3 & d_3 end $$
Тогда решение системы:
Соотношение значений определителей, расположения плоскостей и количества решений:
Три плоскости пересекаются в одной точке
Три плоскости параллельны
Две или три плоскости совпадают или пересекаются по прямой
Бесконечное множество решений
Осталось определить правило вычисления определителя 3-го порядка.
Таких правил несколько, приведём одно из них (так называемое «раскрытие определителя по первой строке»):
$$ Delta = begin a_1 & b_1 & c_1 \ a_2 & b_2 & c_2 \ a_3 & b_3 & c_3 end = a_1 = begin b_2 & c_2 \ b_3 & c_3 end - b_1 = begin a_2 & c_2 \ a_3 & c_3 end + c_1 = begin a_2 & b_2 \ a_3 & b_3 end = $$
$$ = a_1 (b_2 c_3-b_3 c_2 )-b_1 (a_2 c_3-a_3 c_2 )+c_1 (a_2 b_3-a_3 b_2 )$$
Примеры
Пример 1. Найдите решение системы уравнений методом подстановки:
$$<left< begin z = 3x+2y-13 \ 2x-y+3(3x+2y-13) = -2 \ x+2y-(3x+2y-13) = 9 end right.> Rightarrow <left< begin z = 3x+2y-13 \ 11x+5y = 37 \ -2x = -4 end right.> Rightarrow $$
$$Rightarrow <left< begin z = 3cdot2+2cdot3-13 = -1 \ y = frac = 3 \ x = 2 end right.> Rightarrow <left< begin x = 2 \ y = 3 \ z = -1 end right.> $$
$$ <left< begin x = -y-3z+6 \ 2(-y-3z+6)-5y-z = 5\ (-y-3z+6)+2y-5z = -11 end right.> Rightarrow <left< begin x = -y-3z+6 \ -7y-7z = -7 |:(-7) \ y-8z = -17 end right.> Rightarrow $$
$$ Rightarrow <left< begin x = -y-3z+6 \ y+z = 1 \ y-8z = -17 end right.> Rightarrow <left< begin x = -y-3z+6 \ 9z = 18 \ y = 1-z end right.> Rightarrow <left< begin x = 1-6+6 = 1 \ z = 2 \ y = 1-2 = -1 end right.> Rightarrow$$
Пример 2. Найдите решение системы уравнений методом Крамера:
$$ Delta = begin 3 & 2 & -1 \ 2 & -1 & 3\ 1 & 2 & -1 end = 3 = begin -1 & 3 \ 2 & -1 \ end - 2 = begin 2 & 3 \ 1 & -1 \ end - 1 = begin 2 & -1 \ 1 & 2 \ end = $$
$$ Delta_x = begin 13 & 2 & -1 \ -2 & -1 & 3 \ 9 & 2 & -1 \ end = 13 = begin -1 & 3 \ 2 & -1 \ end - 2 = begin -2 & 3 \ 9 & -1 \ end - 1 = begin -2 & -1 \ 9 & 2 \ end = $$
$$ Delta_y = begin 3 & 13 & -1 \ 2 & -2 & 3 \ 1 & 9 & -1 \ end = 3 = begin -2 & 3 \ 9 & -1 \ end - 13 = begin 2 & 3 \ 1 & -1 \ end - 1 = begin 2 & -2 \ 1 & 9 \ end = $$
$$ Delta_z = begin 3 & 2 & 13 \ 2 & -1 & -2 \ 1 & 2 & 9 \ end = 3 = begin -1 & -2 \ 2 & 9 \ end - 2 = begin 2 & -2 \ 1 & 9 \ end + 13 = begin 2 & -1 \ 1 & 2 \ end = $$
$$ Delta = begin 1 & 1 & 3 \ 2 & -5 & -1\ 1 & 2 & -5 end = 1 = begin -5 & -1 \ 2 & -5 \ end - 1 = begin 2 & -1 \ 1 & -5 \ end + 3 = begin 2 & -5 \ 1 & 2 \ end = $$
$$ Delta_x = begin 6 & 1 & 3 \ 5 & -5 & -1 \ -11 & 2 & -5 \ end = 6 = begin -5 & -1 \ 2 & -5 \ end - 1 = begin 5 & -1 \ -11 & -5 \ end + 3 = begin 5 & -5 \ -11 & 2 \ end = $$
$$ = 6(25+2)—(-25-11)+3(10-55) = 162+36-135 = 63 $$
$$ Delta_y = begin 1 & 16 & 3 \ 2 & 5 & -1 \ 1 & -11 & -5 \ end = 1 = begin 5 & -1 \ -11 & -5 \ end - 6 = begin 2 & -1 \ 1 & -5 \ end + 3 = begin 2 & 5 \ 1 & -11 \ end = $$
$$ Delta_z = begin 1 & 1 & 6 \ 2 & -5 & 5 \ 1 & 2 & -11 \ end = 1 = begin -5 & 5 \ 2 & -11 \ end - 1 = begin 2 & 5 \ 1 & -11 \ end + 6 = begin 2 & -5 \ 1 & 2 \ end = $$
Пример 3*. Решите систему уравнений относительно x,y,и z:
$$ a neq b, b neq c, a neq c $$
Решаем методом замены:
$$ <left< begin z = -(a^3+a^2 x+ay)\ b^3+b^2 x+by-(a^3+a^2 x+ay) = 0 \ c^3+c^2 x+cy-(a^3+a^2 x+ay) = 0 end right.> Rightarrow <left< beginz = -(a^3+a^2 x+ay)\ (b^2-a^2 )x+(b-a)y = a^3-b^3 \ (c^2-a^2 )x+(c-a)y = a^3-c^3 end right.> $$
Т.к. $ a neq b$ второе уравнение можно сократить на $(a-b) neq 0$
Т.к.$ a neq c$ третье уравнение можно сократить на $(a-с) neq 0 $. В третьем уравнении после сокращения поменяем знаки:
Из второго уравнения получаем:
Т.к. $b neq c$ можно сократить на $(b-c) neq 0$:
$$ z = -(a^3+a^2 x+ay) = -a^3+a^2 (a+b+c)-a(ab+ac+bc) = $$
$$ = -a^3+a^3+a^2 b+a^2 c-a^2 b-a^2 c-abc = -abc $$
🌟 Видео
Метод Лагранжа. Приведение квадратичной формы к каноническому и нормальному видамСкачать
53. Приведение общего уравнения кривой к каноническому видуСкачать
Привести квадратичную форму к каноническому видуСкачать
Видеоурок "Приведение к каноническому виду"Скачать
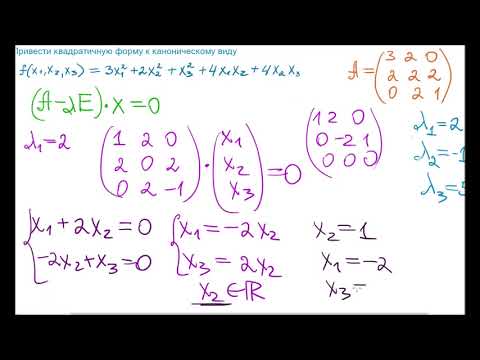
Семинар 6. Приведение уравнения кривой II порядка к каноническому видуСкачать
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
Шапошникова Т. А. - Уравнения с частными производными. Часть 1. Семинары - Семинар 1Скачать
Видеоурок "Параметрические уравнения прямой"Скачать
Шапошникова Т. А. - Уравнения с частными производными. Часть 1. Семинары - Семинар 3Скачать
Приводим диффур в частных производных к каноническому виду | УМФ (УрЧП) | КАК РЕШАТЬ?Скачать
Решение систем с тремя переменными. Практическая часть. 9 класс.Скачать
Каноническое уравнение прямой в пространстве Преход от общего уравненияСкачать
§31.4 Приведение уравнения кривой к каноническому видуСкачать
