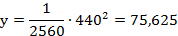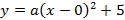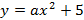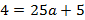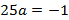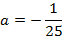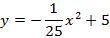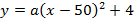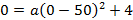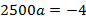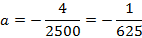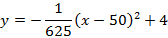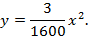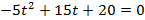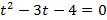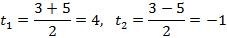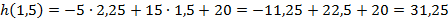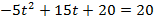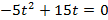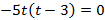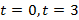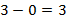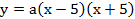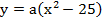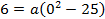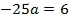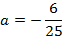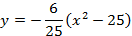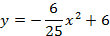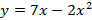Глава III. Кривые второго порядка
Задачи к главе III
3.1. Составьте уравнение окружности:
а) радиуса R = 4 с центром в начале координат;
б) радиуса R = 4 /3 с центром в начале координат;
в) радиуса R = 5 с центром в точке С(—4; 2);
г) радиуса R = 7 /5 с центром в точке D (— 1; — 3 /5)
3.2. Найдите центр и радиус окружности:
3.3. Докажите, что данное уравнение является уравнением окружности. Найдите ее центр и радиус:
3.4. Составьте уравнение окружности, центр которой совпадает с началом координат, если окружность касается прямой х = 3.
3.5. Напишите уравнение окружности, центр которой находится в точке С(3; 7), если известно, что она касается оси Ох.
3.6. Напишите уравнение окружности, центр которой находится в точке пересечения прямых 2х + 3у—13 = 0, х + у— 5 = 0, если она касается оси ординат.
3.7. Напишите уравнение окружности, проходящей через точку N(6 ; 2) с центром в точке С(2; — 1).
3.8. Напишите уравнение окружности, центр которой лежит на оси абсцисс, если окружность касается прямых х =8 и у = 3.
3.9. Напишите уравнение окружности, если известно, что она касается оси абсцисс и прямых х = — 1 и х = 5.
3.10. Напишите уравнение окружности, проходящей через точку М (2; 1) и касающейся осей координат.
3.11. Определите, как расположена точка М(—2; 1) относительно каждой из окружностей (внутри, вне или на окружности):
а) х 2 + у 2 = 2; б) х 2 + у 2 — 5 = 0;
3.12. Определите, как расположена прямая относительно окружности (пересекает, касается или проходит вне ее), если прямая и окружность заданы следующими уравнениями;
а) 2х — у — 3 = 0 и х 2 + у 2 — 3х + 2у — 3 = 0;
б) х — 2у — 1= 0 и (х — 4) 2 + (у + 1) 2 = 5;
в) х + 3у + 10 = 0 и х 2 + у 2 = 1
3.13. Найдите уравнение линии центров двух окружностей
(х — 2) 2 + у 2 = 16 и х 2 + (у — 3) 2 = 9.
3.14. Даны точки M1(2; 3) и М2(10; 9). Напишите уравнение окружности, диаметром которой служит отрезок М1М2.
3.15. Окружность касается оси ординат в начале координат и проходит через точку
М1(— 4; 0). Напишите уравнение окружности и найдите точки пересечения ее с биссектрисами координатных углов.
3.16. Напишите уравнение окружности, проходящей через три точки
М1(0; 0), М2(3; 0) и М3(0; 4).
3.17. Напишите уравнение окружности, описанной около треугольника, стороны которого принадлежат прямым
х — 3у + 1 = 0, 9х — 2у — 41 = 0, 7х + 4у + 7 = 0.
3.18. Определите координаты точек пересечения прямой у — 7х — 12 = 0 и окружности (х — 1) 2 + (у — 2) 2 = 25.
3.19. Напишите уравнение диаметра окружности х 2 + у 2 = 25, перпендикулярного прямой 4х + 3у — 25 = 0.
3.20. Вычислите кратчайшее расстояние от точки A (8; —6) до окружности
х 2 + у 2 — 4 = 0.
3.21. Напишите уравнение окружности, проходящей через точки M(4; 1) и N(0; 5), если известно, что центр ее находится на прямой х + у + 3 = 0.
3.22. Найдите уравнение окружности, симметричной окружности
(х— 1) 2 + (у — 2) 2 = 1 относительно прямой у = х — 3.
3.23. Окружность задана уравнениями: x = √ 2 cos t, y = √ 2 sin t 0 2 + у 2 = 25. Запишите параметрические уравнения этой окружности.
3.25. Окружности заданы уравнениями x = 4 cos t, y = 4 sin t 0 2 + у 2 = 25. Найдите точки пересечения данных окружностей.
3.26. Напишите каноническое уравнение эллипса, если фокальное расстояние равно 8 и эллипс проходит через точку (0; —3).
3.27. Напишите каноническое уравнение эллипса, если его фокус находится в точке
(6; 0) и ось ординат эллипс пересекает в точке (0; —3).
3.28. Докажите, что уравнение 7x 2 + 16у 2 — 112 = 0 является уравнением эллипса. Найдите координаты фокусов и фокальное расстояние.
3.29. Напишите каноническое уравнение эллипса, если:
а) его полуоси равны 7 и 3;
б) его полуоси равны 3 и 4;
в) его большая полуось равна 5, а фокусное расстояние равно 6;
г) его малая полуось равна 4, а фокусное расстояние равно 6.
3.30. Для каждого из следующих эллипсов определите его полуоси, координаты вершин и фокусов:
а) 9x 2 + 16у 2 = 144; б) x 2 + 9у 2 = 4;
в) 4x 2 + 9у 2 =1; г) 0,25x 2 + у 2 = 1.
3.31. Дан эллипс 4x 2 + 25у 2 — 100 = 0. Определите ординаты точек эллипса, абсциссы которых равны — 3.
3.32. Ординаты точек окружности х 2 + у 2 = 36 уменьшены в 3 раза по абсолютной величине. Напишите уравнение полученной новой кривой.
3.33. Дан эллипс 
3.34. Дан эллипс 25x 2 + 49y 2 = 1225. Определите длины осей, координаты фокусов и эксцентриситет.
3.35. Напишите каноническое уравнение эллипса, если его. большая полуось а = 5, а эксцентриситет ε = 3 /5.
3.36. Напишите каноническое уравнение эллипса, у которого расстояния от фокуса до концов большой оси равны 1 и 9.
3.37. Земля движется по эллиптической орбите, в одном из фокусов которой находится Солнце. Вычислите эксцентриситет земной орбиты, если ближайшая к Солнцу точка земной орбиты (перигелий) находится на расстоянии 147 млн. км от Солнца, а наиболее удаленная от Солнца точка орбиты (афелий) находится на расстоянии 152 млн. км от него.
3.38. 9 июля 1980 года в Советском Союзе произведен запуск одной ракетой-носителем восьми искусственных спутников Земли «Космос-1192-1199». Вычислите эксцентриситет орбиты этих искусственных спутников, если все восемь спутников движутся по эллиптической орбите, в одном из фокусов которой находится центр Земли. Максимальное расстояние от поверхности Земли — 1522 км; минимальное расстояние от поверхности Земли — 1451 км. Средний радиус Земли приближенно равен 6371 км.
3.39. Напишите каноническое уравнение эллипса, если эллипс проходит через точку
М(2; —2), а его большая полуось равна 4.
3.40. Найдите эксцентриситет эллипса
3.41. Найдите каноническое уравнение эллипса, касающегося в концах своей большой оси окружности х 2 + у 2 = 100, если известно, что а = 2b.
3.42. Вычислите площадь четырехугольника, две вершины которого находятся в фокусах эллипса 9х 2 + 25y 2 — 225 = 0, а две другие вершины совпадают с концами его малой оси.
3.43. Сторона ромба равна 10. Через две противоположные его вершины проходит эллипс, фокусы которого совпадают с двумя другими вершинами ромба. Напишите уравнение эллипса, приняв диагонали ромба за оси координат, если координаты фокуса (8; 0)
3.44. Определите длину хорды эллипса 
3.45. Дан эллипс 15х 2 + 25y 2 — 375 = 0. Через фокус проведен перпендикуляр к его большой оси. Определите расстояния от точек пересечения этого перпендикуляра с эллипсом до фокусов.
3.46. Составьте параметрические уравнения эллипса 4х 2 + 9y 2 — 36 = 0.
3.47. Даны параметрические уравнения эллипса
Запишите его каноническое уравнение.
3 48, Найдите уравнения касательных к эллипсу 9х 2 + 25y 2 = 225, угловой коэффициент которых равен 3 /5
3.49. Найдите точку касания прямой 5х — 2у — 30 = 0 с эллипсом
75х 2 + 24y 2 — 1800 = 0.
3.50. Дан эллипс 25х 2 + 36y 2 — 900 = 0 и окружность х 2 + y 2 = 25. Найдите точки их пересечения.
3.51. Напишите уравнение касательной к эллипсу в точке (3; —3), если его уравнение 36х 2 + 12y 2 — 432 = 0.
3.52. Напишите каноническое уравнение гиперболы, если фокальное расстояние равно 30 и гипербола проходит через точку (—9; 0).
3.53. Напишите каноническое уравнение гиперболы, если ее фокус находится в точке
(— 5√ 2 ; 0) и ось абсцисс гипербола пересекает в точке (6; 0).
3.54. Докажите, что уравнение 11х 2 — 25 y 2 — 275 = 0 является уравнением гиперболы. Найдите координаты фокусов.
3.55. Определите полуоси каждой из следующих гипербол!
a) 
в) х 2 — 9y 2 = 9; г) 16х 2 — 9y 2 = 1;
д) х 2 — y 2 = 4; е) 9х 2 — 16y 2 = 144.
3.56. Для гиперболы 9х 2 — 16y 2 — 144 = 0 найдите:
б) координаты фокусов;
в) координаты вершин;
г) уравнения асимптот.
3.57. Напишите каноническое уравнение гиперболы, если:
а) ее действительная полуось равна 4, а мнимая — 13;
б) фокальное расстояние равно 16, а мнимая полуось — 6;
в) фокальное расстояние равно 6, а ε = 1,5;
г) действительная полуось равна 8, a ε = 5 /4;
д) уравнение асимптоты у = 3 /2 х, а действительная полуось равна 2;
е) мнимая полуось равна 3, а ε = 5 /4 .
3.58. Напишите каноническое уравнение гиперболы, если расстояния от одной из ее вершин до фокусов равны 9 и 1.
3.59. Дана гипербола 
3.60. Найдите асимптоты гиперболы 
3.61. Найдите асимптоты гиперболы х 2 — y 2 = 9. Постройте гиперболу и вычислите ее эксцентриситет.
3.62. Дано уравнение гиперболы 9х 2 —16 y 2 = 144. Найдите координаты ее фокусов и вершин, эксцентриситет и уравнение асимптот. Сделайте чертеж.
3.63. Составьте каноническое уравнение гиперболы, действительная полуось которой равна 5, а эксцентриситет 1,4.
3.64. Определите, при каком условии асимптоты гиперболы 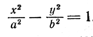
3.65. Составьте каноническое уравнение гиперболы, если уравнение ее асимптоты
у = 1 /2 х, а один из фокусов находится в точке (—5; 0).
3.66. Напишите каноническое уравнение гиперболы, зная, что асимптоты ее имеют уравнения у = ± 2х, а фокусное расстояние равно 10.
3.67. Дана гипербола 
3.68. Составьте уравнение гиперболы, фокусы которой находятся в вершинах эллипса 
3.69. Фокусы гиперболы совпадают с фокусами эллипса 9х 2 + 25у 2 — 225 = 0. Составьте уравнение гиперболы, если ее эксцентриситет равен 2.
3.70. Найдите уравнения касательных к гиперболе х 2 — у 2 = 1, угловой коэффициент которых равен 2.
3.71. Эксцентриситет траектории движения первой советской космической ракеты, запущенной в сторону Луны 2 января 1959 г. равен 1,05. Определите вид траектории ракеты.
3.72. Напишите уравнение параболы, если координаты фокуса (4; 0), а уравнение директрисы х + 4 = 0.
3.73. Напишите каноническое уравнение параболы, проходящей через точку (5; 3).
3.74. Дана парабола у 2 = 5х. Найдите точки параболы, расстояние от которых до фокуса равно 4.
3.75. Составьте каноническое уравнение параболы, у которой фокус находится в точке пересечения прямой 2х — 5у — 8 = 0 с осью абсцисс. Постройте эту параболу.
3.76. Составьте каноническое уравнение параболы, проходящей через точку N(9; 6), определите угол 
3.77. Найдите точки пересечения параболы у 2 = 4х и прямых:
а) х = у; б) х = — у;
3.78. Напишите уравнение касательной к параболе у 2 = 6х в точке (6; 6).
3.79. Напишите уравнение окружности, центр которой совпадает с фокусом параболы
у 2 = 8х, если известно, что окружность касается директрисы параболы. Определите координаты точек пересечения параболы и окружности и постройте чертеж.
3.80. Приведите уравнение эллипса 
3.81. Дана гипербола ху = 2. Приведите ее уравнение к каноническому виду.
3.82. Приведите уравнение параболы 3у = х 2 + 4х — 11 к каноническому виду.
3.83. Для каждого из следующих эллипсов определите его полуоси, координаты вершин и координаты фокусов:
а) 12х 2 + 5у 2 — 60 = 0;
б) 16х 2 + 9у 2 — 144 = 0;
3.84. Напишите уравнение эллипса, симметрично расположенного относительно осей координат с фокусами на оси Оу, если:
а) его полуоси равны 3 и 4;
б) его полуоси равны 6 и 3;
в) его большая полуось равна 8, а фокусное расстояние равно 6;
г) его малая полуось равна 4, а эксцентриситет ε = 3 /5;
д) его малая полуось равна 6, а фокусное расстояние равно 8.
3.85. Напишите уравнение эллипса, у которого сумма полуосей равна 8 и расстояние между фокусами равно 8. Фокусы лежат на оси ординат и расположены симметрично относительно точки (0; 1).
3.86. Дан эллипс 16х 2 + 7у 2 — 112 = 0. Определите координаты точек эллипса, расстояние которых до фокуса равно 2,5.
3.87. Окружность (x — 5) 2 + (у — 3) 2 = 4 касается эллипса и проходит через его фокусы. Составьте уравнение эллипса, если его большая ось параллельна оси абсцисс.
3.88. Составьте уравнение гиперболы, расположенной симметрично относительно осей координат, с фокусами на оси ординат, если
а) полуоси равны 3 и 6;
в) уравнение асимптоты у = 12 /5 х, а действительная полуось равна 24;
г) ε = 5 /3 , а мнимая полуось равна 4.
3.89. Для гиперболы 9х 2 — 16у 2 = — 144 найдите: а) полуоси; б) координаты вершин; в) координаты фокусов; г) уравнения асимптот.
3.90. Напишите уравнение гиперболы, у которой расстояние между вершинами равно 24, а фокусы имеют координаты (— 10; 2) и (16; 2).
3.91. Составьте уравнение гиперболы, если ее полуоси равны 5 и 4, центр имеет координаты (3; 2), а действительная ось параллельна оси абсцисс.
3.92. Напишите уравнение параболы с вершиной в начале координат, если:
а) парабола расположена в верхней полуплоскости симметрично относительно оси ординат и фокальный параметр равен 4;
б) парабола расположена в нижней полуплоскости симметрично относительно оси ординат и фокальный параметр равен 6;
в) парабола расположена в правой полуплоскости симметрично относительно оси абсцисс, а ее фокальный параметр равен 3;
г) парабола расположена в левой полуплоскости симметрично относительно оси абсцисс, а ее фокальный параметр равен 5.
3.93. Напишите уравнение параболы, проходящей через начало координат и симметричной относительно оси ординат, если координаты фокуса F(0; —3).
3.94. Фокус параболы имеет координаты F(— 6; 0), а уравнение директрисы х — 6 = 0. Составьте уравнение параболы.
3.95. Найдите уравнение параболы, зная, что ее вершина находится в точке А(—4; 5), а фокус в точке В(—2; 5). Напишите уравнение ее оси и директрисы.
3.96. Дан фокус параболы (— 3; — 4) и уравнение ее директрисы х + 1 = 0. Напишите уравнение параболы и найдите точки пересечения параболы с осями координат.
3.97. Определите координаты точки, которая лежит на параболе х 2 = 8у, если расстояние до этой точки от директрисы равно 4.
3.98. Постройте на одном чертеже следующие параболы:
х 2 = 1 /2 у х 2 = у , х 2 = 2у.
3.99. Фокус параболы лежит в точке F (0; 1 /4) , директриса параллельна оси абсцисс и отсекает на оси ординат отрезок, длина которого равна 1 /4 . Напишите уравнение параболы.
3.100. Парабола проходит через точки A(0; 6) и В (4; 0) симметрично относительно оси абсцисс. Напишите уравнение параболы и постройте ее.
3.101. Составьте уравнение параболы и напишите уравнение ее директрисы, если парабола проходит через точки пересечения прямой у = х и окружности х 2 + y 2 — 10у = 0 и симметрична относительно оси ординат. Постройте окружность, прямую и параболу.
3.102. Напишите уравнение касательной к параболе х 2 = 6у в точке (2; 2 /3).
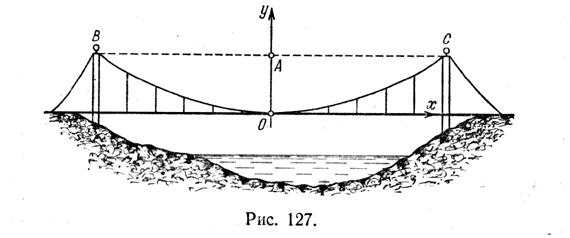
3.103. Канат подвесного моста имеет форму параболы (рис.127). Требуется составить ее уравнение относительно указанных на рисунке осей координат, если прогиб каната
| OA | = 10, а длина моста | ВС | = 60.
3.104. Какое множество на плоскости задано следующими уравнениями второго порядка:
a) 3х 2 + 4y 2 = 12; б) 3х 2 — 4y 2 = 12;
д) 25х 2 — 9y 2 = 0; е) 5y 2 — 125 = 0;
ж) 36х 2 + 49y 2 = 0; з) х 2 + (у — 2) 2 = 7;
Видео:§24 Каноническое уравнение параболыСкачать

Дополнение к разделу I РАВНОВЕСИЕ ГИБКИХ НЕРАСТЯЖИМЫХ ПОДВЕСНЫХ НИТЕЙ
Знание основных определений и зависимостей при равновесии подвешенных по концам между двумя опорами нитей/тросов/це- пей (находящихся под действием вертикальной нагрузки) является важным в инженерной практике. Далее будут рассматриваться задачи в предположениях, что заданы величины пролета /, прове- сов/провисаний а также эпюра распределенной нагрузки аЛ’ВЪ (рис. 1.1.доп).
Рис. 1.1.доп. К основным определениям при исследовании подвесных цепей
При исследовании равновесия тросов или цепей надо ответить, как правило, на два вопроса: 1) какова будет форма кривой, которую займет цепь или трос в положении равновесия? 2) чему равно натяжение цепи/троса в любой точке кривой?
Для ответа на поставленные вопросы рассмотрим равновесие участка CD нити (рис. 1.2.доп, а). Точка С — нижняя точка кривой, точка D — произвольная точка нити с координатами (х, у).
Отсеченный участок CD, который можно рассматривать на основании принципа отвердевания как твердое тело, находится в равновесии под действием трех сил: вертикальной силы Q, представляющей собой равнодействующую распределенной нагрузки на участке CD, и двух растягивающих усилий Н и Т, являющихся реакциями со стороны каждого из отброшенных участков нити (рис. 1.2.доп, б). Силы Ни Тнаправлены по касательной к кривой соответственно в точках Си D. Вертикальная сила Q проходит через
Рис. 1.2.доп. Равновесие подвешенной цепи
центр тяжести той части эпюры, которая расположена между рассматриваемыми сечениями.
Эти три силы должны образовать замкнутый силовой треугольник, показанный на рис. 1.2.доп, в. Из этого треугольника находим
С другой стороны,
Уравнения (1) и (2) являются основными при расчете гибких подвесных цепей. В этих уравнениях сила Н постоянна, а сила Q является функцией от х.
Уравнение (1) является ДУ кривой в положении равновесия и после интегрирования дает ответ на первый поставленный вопрос. Второе уравнение отвечает на второй вопрос.
- ? Относительно характера внешней нагрузки на нить следует отметить следующее. На практике наиболее часто встречаются два случая распределения нагрузки:
- 1) тонкий трос или легкая цепь подвержены воздействию равномерной нагрузки, приложенной с помощью вертикальных подвесок (рис. 1.3.доп). Обычно эта нагрузка велика по сравнению с весом самого троса, и можно считать, что она распределена равномерно по всей длине горизонтального пролета;
- 2) гибкая нить свободно висит в поле сил тяжести, находясь только под действием собственного веса (рис. 1.4.доп). Эпюра та-
Рис. 1.3.доп. Тонкая цепь под действием вертикальной равномерной нагрузки (параболическая нить)
Рис. 1.4.доп. Цепь под действием собственного веса (цепная линия)
кой нагрузки определяется, очевидно, видом кривой, форму которой принимает нить.
В первом случае нагруженная нить принимает форму параболы, во втором — цепной линии. Приведем основные формулы для определения характеристик нити в обоих случаях.
Если на нить действует равномерно распределенная по длине пролета / вертикальная нагрузка интенсивностью q (см. рис. 1.3.доп), то уравнение равновесной кривой нити при выбранном направлении осей примет вид
То есть нить образует участок параболы с вертикальной осью.
Натяжение нити вдоль кривой изменяется в соответствии с уравнением
откуда следует, что натяжение нити будет минимальным в самой нижней точке С, где оно равно Я, и что оно увеличивается к концам нити, достигая максимума в верхней опоре.
Силы натяжения на концах нити равны:
где расстояния определяются из уравнения (3): 
Сила минимального натяжения Я, точнее, ее модуль, определяется по формуле 2
В важном частном случае, когда обе опоры находятся на одном уровне, имеем:
Будем считать, что нить свободно подвешена в поле сил тяжести и подвержена действию только собственного веса, равномерно распределенного по длине нити (см. рис. 1.4.доп). Введем следующие обозначения: q — вес единицы длины нити; S — длина дуги CD (фактически это дуговая координата, если она отсчитывается со знаками «±», в зависимости от направления дуги). Тогда связь между координатами s и х точки D дается уравнением [1] [2] [3]
Длина нити L между опорами равна
Уравнение равновесной кривой нити имеет вид
Это уравнение цепной линии с вертикальной осью.
Натяжение нити в произвольной точке D равно
Из этого уравнения видно, что натяжение Т будет минимальным в нижней точке нити, затем оно увеличивается к концам нити и достигает наибольшей величины в верхней опоре.
Натяжения на концах равны:
Расстояния определяются из формул:
Наконец, величина Н определяется из формулы
с помощью таблиц гиперболических функций.
При решении задач на равновесие гибких нерастяжимых нитей можно пользоваться следующей методикой:
- 1) определить вид нагрузки, действующей на нить(собственный вес нагрузка, равномерно распределенная по горизонтальному пролету, и др.)’,
- 2) выбрать СК и составить ДУравновесия нити и уравнение для растягивающего усилия Т;
- 3) проинтегрировав уравнение равновесия, найти уравнение равновесной кривой нити’,
- 4) в зависимости от конкретных условий задачи найти искомые параметры.
Пример 1. На рис. 1.5.доп, а изображен трос подвесного моста, несущий равномерно распределенную по его горизонтальной длине / нагрузку Q — 54 т.
Рис. 1.5.доп.Трос подвесного моста
Определить вид кривой, которую займет трос, и максимальное натяжение троса, если /= 30 м, /= 3,6 м,Л = Зм.
Решение. Выбираем СК, помещая начало в нижней точке троса С и направляя ось х горизонтально вправо, а ось у — вертикально вверх (рис. 1.5.доп, б, 1.6.доп). Провисания троса, очевидно, равны/, =/2, /2 =/+ /г. Интенсивность равномерно распределенной нагрузки q = Q/l- = 1,8 т • м -1 .
Рис. 1.б.доп. Канат под действием вертикальной нагрузки
Чтобы написать уравнение равновесной кривой троса, воспользуемся уравнением (1).
В данном случае сила Q равна
и уравнение принимает вид 
Поскольку при выбранной СК при х = 0 координата у = 0, произвольная постоянная С2 = 0, и уравнение равновесной кривой троса будет
Это уравнение параболы с вертикальной осью и с вершиной в точке С. Для нахождения натяжения троса Т воспользуемся уравнением (2), которое примет вид
Поскольку, как это следует из формулы, натяжение возрастает по мере удаления от точки С, максимальное натяжение троса будет иметь место в точке В и составит величину
где b — расстояние точки С от опоры В, взятое по горизонтали.
Для нахождения неизвестных пока величин b, Н можно воспользоваться формулами (6) и (7): проделаем это подробнее.
Применив уравнение равновесной кривой троса (а) к точкам Л, В, найдем:
Вычтя первое уравнение из второго, получим
Одновременно имеем, что а + Ь-1.
Из последних двух уравнений следует:
Выражение для нахождения величины Н может быть найдено подстановкой полученного значения для b во второе уравнение системы (б).
Получаем:
Решая это квадратное уравнение, находим: 
уравнении следует принять знак «плюс», так как вершина параболы лежит между опорами. Следовательно, минимальное натяжение равно:
Величину b можно теперь найти либо из второго уравнения (б), либо из второго уравнения (в). Воспользовавшись последним, получаем:
Теперь уравнение (а) равновесной кривой троса принимает вид: у = 0,0222х?.
Максимальное натяжение троса: Ть
Пример 2. Канат несет нагрузку в 150 кг на каждый метр длины горизонтального пролета (рис. 1.6.доп, а). Определить максимальное растягивающее усилие в канате, если натяжение в точке В в 2 раза больше, чем в точке А. Размеры конструкции даны на рис. 1 .б.доп, а.
Решение. Предположим, что вершина С параболы, определяющей положение равновесия каната, лежит слева от обеих опор (рис. 1.б.доп, б).
Обозначим, как обычно, через а, b расстояния опор Л, В от вершины С по горизонтали, а через/j,/2 эти же расстояния по вертикали.
Имеем очевидные равенства:
В задаче указано, что натяжение каната в точке В в 2 раза больше, чем в точке А. Запишем это условие в виде уравнения, использовав непосредственно формулы (5) и учитывая равенство (а). Имеем
где Н — натяжение каната в точке С, кг; q — интенсивность распределенной нагрузки, кг • м» 1 . В этом уравнении два неизвестных — а, Н. Для их определения необходимо составить еще одно уравнение. Оно получается из (б), если величины/,,/, выразить по формулам (6а) и учесть снова равенство (а):
Возводя обе части уравнения (в) в квадрат и раскрывая скобки в левой части уравнения (г), получим после некоторых упрощений:
Из второго уравнения этой системы находим
Подставляя это значение в первое уравнение системы (д), получаем квадратное уравнение
откуда
Таким образом, имеется два значения а. Выбрав положительное значение, находим а
0,823 м. Из уравнения (е) определяем Н: Н
573,4 кг. Возвратившись опять ко второй формуле (д), находим искомое максимальное усилие в канате Ть = 1173 кг. В этом случае вершина параболы С лежит слева от обеих опор (см. рис. 1.6.доп, б). Если же выбрать второй отрицательный корень, то а
—1,823 м и вершина параболы лежит между опорами. Для этого случая находим:
Пример 3. Гибкая нить длиной 30 м и весом единицы длины 7,5 кг/м свободно подвешена к двум опорам, находящимся на взаимном расстоянии 15 м и на одном уровне. Определить стрелу провисания в середине пролета и максимальное натяжение нити.
Решение. Изобразим схематически равновесное положение нити (рис. 1.7.доп). В задаче заданы: расстояние между опорами /, длина всей нити L и вес единицы длины нити q. Здесь имеет место второй основной случай нагружения, когда нить принимает форму цепной линии.
Рис. 1.7.доп. Гибкая нить под собственным весом
Для определения величины провисания нити/необходимо составить уравнение равновесной кривой нити. Выбрав СК Сху, как показано на рис. 1.7.доп, воспользуемся основным ДУ (1), которое принимает вид
где s — длина дуги CD.
Для интегрирования этого уравнения надо предварительно выразить длину 5 как функцию координат л:, у. Для этого используем известное соотношение
которое после подстановки в него значения dy/dx из уравнения (а) примет вид
Проинтегрировав это уравнение, получим
Постоянная интегрирования С, определяется из условия, что для выбранной СК 5 = 0 при х = 0. Отсюда С, = 0. Тогда уравнение (б) принимает вид
Подставив это выражение для s в уравнение (а), получаем ДУ равновесной кривой нити:
После интегрирования найдем:
Поскольку при х = 0 координата у = 0, получаем С, = — H/q и окончательно
Теперь мы имеем все уравнения, необходимые для решения задачи. Действительно, положив в уравнении (в) х = 1/2, получим
или, после подстановки числовых значений,
Это уравнение вида 2z = sh(^). С помощью таблиц гиперболического синуса находим подбором его решение [4] : 
25,84 кг. Искомое провисание нити найдется теперь из уравнения (г), если принять х = //2:


в уравнение (2), получимили, используя соотношение (4),
Из последнего уравнения следует, что натяжение нити достигает максимума в точках закрепления А, В, где оно равно
Пример 4. Часть гибкой нити с равномерно распределенным по длине весом лежит на горизонтальной плоскости. Остальная часть нити проходит над небольшим блоком А (рис. 1.8.доп, а). К концу нити прикладывается постепенно увеличивающаяся сила Т. При этом длина линии контакта ВС нити с плоскостью уменьшается и стремится к какому-то определенному пределу с, при котором начинается скольжение нити по плоскости. Определить это предельное значение с, если d — 60 м, /, = 6 м, коэффициент трения между нитью и плоскостью/, = 0,5.
Рис. 1.8.доп. К примеру 4
Решение. Участок АВ нити, который примет форму цепной линии, изображен схематически на рис. 1.8.доп, б. При решении этой задачи будем пользоваться данными в начале пособия, учитывая, что в этом случае точка В является нижней точкой кривой.
Следовательно, во всех этих формулах надо положить а = I, b = 0, /2 = 0, Т„ = Н, Та=Т.
С увеличением силы Твозрастает и натяжение нити Н в точке В. Нить начнет скользить, когда это натяжение станет равным силе трения между участком ВС нити и плоскостью.
Запишем это условие в виде уравнения
где q — вес единицы длины нити.
Величина Я должна удовлетворять уравнению (14), которое в данной задаче принимает вид
Исключая из уравнений (а) и (б) величину Я, получаем уравнение
из которого и определяется искомый размер с. Поскольку 1 = d — с, это уравнение можно записать в виде
или, подставляя сюда известные величины,
Разрешить это трансцендентное уравнение относительно с помощью точных алгебраических методов не представляется возможным. Поэтому для нахождения его корней приходится пользоваться приближенными способами. Рассмотрим два таких способа: графический и метод итераций.
Графический способ заключается в том, что на одном чертеже строятся графики левой и правой частей уравнения. Абсциссы точек пересечения этих графиков и дают приближенные значения корней. Для некоторого упрощения представим сначала уравнение (в) в виде
Графиком левой части уравнения (г) является биссектриса первого координатного угла. Для построения графика правой части вычислим ее величину при нескольких значениях с, взятых около предполагаемого значения корня. Результаты вычислений сведены в таблице ниже.
По данным таблицы построен рис. 1.8.доп, в, из которого следует, что искомое значение с равно 44,1.
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Урок_3_Решение текстовых задач_Методические рекомендации
Методические рекомендации к уроку №3
темы/подраздела « Квадратичная функция и ее график »
раздела « Квадратичная функция»
Тема урока: Решение текстовых задач
8. 4 .2.3 использовать квадратичную функцию для решения прикладных задач;
8.4.3.1 составлять математическую модель по условию задачи.
На данном уроке учащиеся продолжат работу по развитию навыка решения задач с использованием квадратичной функции.
Методические рекомендации по организации урока. Рекомендации по формативному оцениванию
В начале урока учащимся предлагается тестовые задания для организации повторения пройденного материала. Учитель заранее готовит сигнальные карточки трех цветов для каждого ученика. Их использование позволит учителю быстро оценить понимание учащимися определенного материала. Допущенные ошибки сразу анализируются.
Затем проводится письменная работа, она с совместного разбора задания на составление уравнения функции и поиска ответа на вопрос задачи. Учитель вовлекает всех учащихся в диалог. Для первоначального закрепления учащиеся решают задачу в группах. Здесь нужно нацелить их на то, что каждый ученик после обсуждения должен уметь объяснить решение задачи свой группы. Процесс объяснения другим учащимся позволит глубже разобраться в решении. Также здесь нужно поощрять учащихся, задающих вопросы. Учитель обходит класс, слушает объяснения, помогает в корректном применении математического языка.
Два задания подготовлены для самостоятельного решения учащимися. Учитель обходит класс, дает советы учащимся. Он может также привлекать других учащихся для консультирования тех, кто испытывает затруднения.
Ответы и решения
Мост Голден Гейт через пролив Золотые ворота находится в Сан-Франциско (США). Мост построен по проекту инженера Йозефа Штрауса. Строительство началось в 1933 году и было закончено через 4 года. Мост установил два рекорда: как самый длинный и как самый высокий мост.
Длина основного пролета моста (расстояние между опорами) 1280 м, высота опор над уровнем проезжей части моста – 160 м. Кабель, поддерживающий мост, имеет форму параболы и касается проезжей части в середине пролета. На какой высоте находится кабель на расстоянии 200 м от опоры моста?
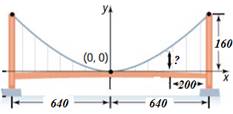
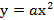
Точка (640, 160) – расположена на одной из опор, отсюда 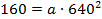
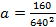
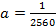
Тогда уравнение параболы имеет вид: 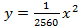
Кабель находится на расстоянии 200 м от опоры моста, следовательно, в 440 м от вершины параболы.
Задание для группы 1
Дорога проходит под параболической аркой, как показано на рисунке. Самая высокая часть арки – 5 м. Ширина дороги – 10м, а высота – 4 м. Составьте квадратичную функцию, задающую форму арки.
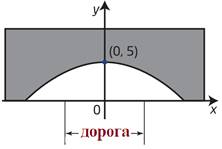
Запишем уравнение параболы в виде 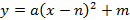
Ширина дороги – 10м, а высота – 4 м, значит парабола проходит через точку 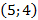
Ответ : 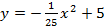
Задание для группы 2
Небольшие мосты имеют форму параболы. На рисунке представлен один из таких мостов. Составьте уравнение параболы, определяющей форму этого моста.
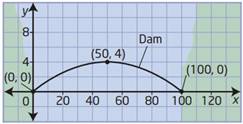
Запишем уравнение параболы в виде 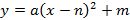
Парабола проходит через точки 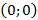
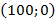
Ответ : 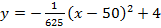
Задание для группы 3
Длина моста 400 м, а высота опор 75 м. Напишите уравнение параболы, являющейся моделью для подвесного кабеля, удерживающего этот мост.

Построим координатную плоскость, так чтобы ось х проходила вдоль проезжей части моста, а ось у – вдоль оси симметрии. Тогда вершина параболы имеет координаты (0, 0), значит функция задается формулой 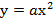
Парабола проходит через точку (200; 75), тогда 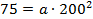
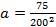
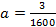
Тогда уравнение параболы имеет вид:
1. Тело брошено вертикально вверх. Высота ( h ), на которой находится тело через t секунд полета, вычисляется по формуле 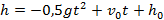
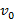
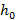
Составьте формулу, задающую эту зависимость, если h0 = 20, v0 = 15 и постройте график.
Используя график, ответьте на вопросы:
а) Сколько времени тело двигалось вверх?
б) Сколько времени тело двигалось вниз?
в) На какую максимальную высоту поднялось тело?
г) В течении какого времени тело находилось на высоте более 20 м?
Функция имеет вид 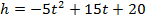
а) 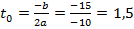
б )
Через 4 с тело упало на землю.
Тело двигалось вниз 2,5 с.
в)
г )
Ответ: Тело находилось на высоте более 20 м в течение 3 с.
2. Двух полосная дорога со встречным движением проходит под аркой шириной 10 м. Самая высокая точка арки расположена на высоте 6 м. Сможет ли грузовик, высота которого 4,5 м, а ширина 3 м, проехать под этой аркой? Ответ объясните.
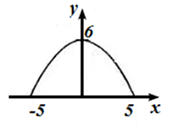
Если расположить координатную плоскость, так чтобы ось х проходила вдоль проезжей части дороги, а ось у – вдоль оси симметрии, тогда вершина параболы имеет координаты (0, 6) . Парабола проходит через точки 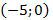
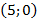
Подставив координаты точки 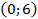
Ширина грузовика 3 м, тогда при 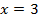
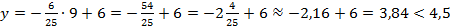
Ответ: Грузовик может проехать под этой аркой .
Найдите наибольшее или наименьшее значение функции.
a) 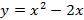
b) 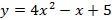
c)
Определите коэффициенты функции 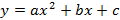
а) 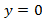
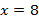
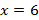
б) 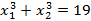
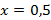
в) наименьшее значение функции, равное 7, достигается при 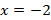
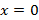
Список полезных ссылок и литературы
1. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений. – М.: Мнемозина, 2010
2. Виленкин Н.Я., Сурвилло Г.С. Алгебра. 9 класс. учеб. Для учащихся с углубленным изучением математики. / 7-е изд. — М.: Просвещение, 2006.
🔥 Видео
213. Фокус и директриса параболы.Скачать

Как найти вершину параболы?Скачать

КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать

§25 Исследование канонического уравнения параболыСкачать

Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Как легко составить уравнение параболы из графикаСкачать

Видеоурок "Гипербола"Скачать

Парабола (часть 1). Каноническое уравнение параболы. Высшая математика.Скачать

Как определить уравнение параболы по графику?Скачать

Видеоурок "Парабола"Скачать

Фокус и директриса параболы 1Скачать

Вершина параболы и ось симметрии. ПримерСкачать

Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Уравнение параболы #алгебра #графики #парабола #репетиторСкачать

Как написать уравнение параболы с помощью графикаСкачать

Фокус и директриса параболы 2Скачать

Вариант 72, № 5. Уравнение оси симметрии параболы. Пример 2Скачать