Калькулятор уравнение перпендикуляра опущенного из точки (8 видео)

Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости онлайн

С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через данную точку и перпендикуляной данной плоскости. Дается подробное решение с пояснениями. Для построения уравнения прямой введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».

Содержание

Предупреждение
Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости
Уравнение перпендикулярной прямой
Онлайн калькулятор. Расстояние от точки до плоскости
Найти расстояние от точки до плоскости
Ввод данных в калькулятор для вычисления расстояния от точки до плоскости
Дополнительные возможности калькулятора для вычисления расстояния от точки до плоскости
Теория: Расстояние от точки до плоскости
🌟 Видео

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать

Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости

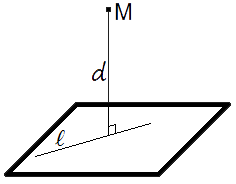
Наша цель построить уравнение прямой, проходящей через данную точку M₀ и перпендикулярной к данной плоскости Ax+By+Cz+D=0.

Общее уравнение плоскости имеет вид:

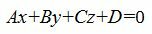Калькулятор уравнение перпендикуляра опущенного из точки

(1)

где n(A,B,C)− называется нормальным вектором плоскости.

Уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:

(2)

Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .

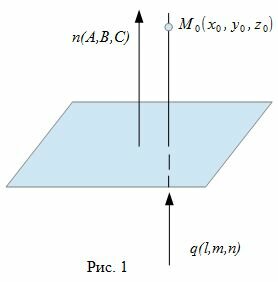Таким образом, уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и ортогональный плоскости (1) имеет следующий вид:

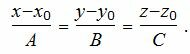(3)

Пример 1. Построить прямую, проходящую через точку M₀(5, -4, 4) и перпендикулярной плоскости

Общее уравнение плоскости имеет вид (1), где :

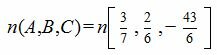(4)

Подставляя координаты точки M₀(5, -4, 4) и координаты нормального вектора плоскости (4) в (3), получим:

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Уравнение перпендикулярной прямой

Альтернативная формула
Прямая, проходящая через точку M₁(x₁; y₁) и перпендикулярная прямой Ax+By+C=0 , представляется уравнением

назначение сервиса . Онлайн-калькулятор предназначен для составления уравнения перпендикулярной прямой (см. также как составить уравнение параллельной прямой).

Пример №1 . Составить уравнение прямой, проходящей через точку (2; -1) и перпендикулярной 4x-9y=3 .
Решение. Данную прямую можно представить уравнением y = 4 /₉x – 1 /₃ (a = 4 /₉). Уравнение искомой прямой есть y+1 = -9/4(x-2) , т.е. 9x+4y-14=0 .

Пример №2 . Решая пример 1 (A=4, B=-9) по формуле (2), найдем 4(y+1)+9(x-2)=0 , т.е. 9x+4y-14=0 .

Пример №3 . Составить уравнение прямой, проходящей через точку (-3, -2) перпендикулярно прямой 2y+1=0 .
Решение. Здесь A=0, B=2. Формула (2) дает -2(x+3)=0, т.е. x+3=0 . Формула (1) неприменима, так как a=0 .

Видео:Задача 7. Найти расстояние от точки M0 до плоскости, проходящей через три точки M1, M2, M3.Скачать

Онлайн калькулятор. Расстояние от точки до плоскости

Предлагаю вам воспользоваться онлайн калькулятором для вычисления расстояния от точки до плоскости.

Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление расстояния от точки до плоскости и закрепить пройденный материал.

Видео:Задача 8. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору.Скачать

Найти расстояние от точки до плоскости

Ввод данных в калькулятор для вычисления расстояния от точки до плоскости

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления расстояния от точки до плоскости

Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.

Теория: Расстояние от точки до плоскости

Расстояние от точки до плоскости — равно длине перпендикуляра, опущенного из точки на плоскость.

Если задано уравнение плоскости A x + B y + C z + D = 0, то расстояние от точки M(M _x , M _y , M _z ) до плоскости можно найти используя следующую формулу

d =	\|A·M _x + B·M _y + C·M _z + D\|
	√ A 2 + B 2 + C 2

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.