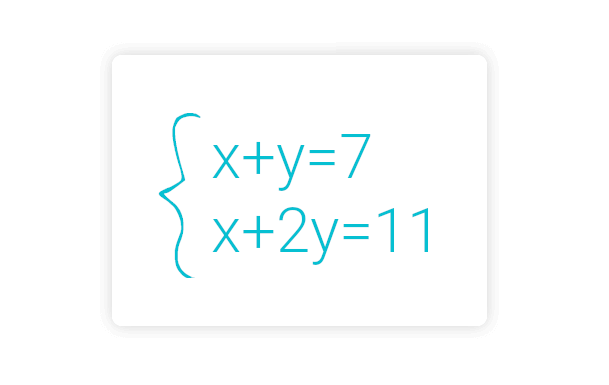Калькулятор систем уравнений с корнями

Видео:Система иррациональных уравнений #1Скачать

Иррациональные уравнения онлайн калькулятор

Наш калькулятор поможет вам решить иррациональное уравнение или неравенство. Искусственный интеллект, который лежит в основе калькулятора, даст ответ с подробным решением и пояснениями.

Калькулятор полезен старшеклассникам при подготовке к контрольным работам и экзаменам, для проверки знаний перед ЕГЭ, родителям школьников с целью контроля решения многих задач по математике и алгебре.

Видео:Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

Добро пожаловать на сайт Pocket Teacher

Наш искусственный интеллект решает сложные математические задания за секунды

Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

начать

Видео:10 класс. Алгебра. Системы уравненийСкачать

Иррациональные уравнения

Что такое иррациональные уравнения и как их решать

Уравнения, в которых переменная содержится под знаком радикала или под знаком возведения в дробную степень, называются иррациональными. Когда мы имеет дело с дробной степенью, то мы лишаем себя многих математических действий для решения уравнения, поэтому иррациональные уравнения решаются по-особенному.

Иррациональные уравнения, как правило, решают при помощи возведения обеих частей уравнения в одинаковую степень. При этом возведение обеих частей уравнения в одну и ту же нечетную степень – это равносильное преобразование уравнения, а в четную – неравносильное. Такая разница получается из-за таких особенностей возведения в степень, таких как если возвести в чётную степень, то отрицательные значения “теряются”.

Смыслом возведения в степень обоих частей иррационального уравнения является желание избавиться от “иррациональности”. Таким образом нам нужно возвести обе части иррационального уравнения в такую степень, чтобы все дробные степени обоих частей уравнения превратилась в целые. После чего можно искать решение данного уравнения, которое будет совпадать с решениями иррационального уравнения, с тем отличием, что в случае возведения в чётную степень теряется знак и конечные решения потребуют проверки и не все подойдут.

Таким образом, основная трудность связана с возведением обеих частей уравнения в одну и ту же четную степень – из-за неравносильности преобразования могут появиться посторонние корни. Поэтому обязательна проверка всех найденных корней. Проверить найденные корни чаще всего забывают те, кто решает иррациональное уравнение. Также не всегда понятно в какую именно степень нужно возводить иррациональное уравнение, чтобы избавиться от иррациональности и решить его. Наш интеллектуальный калькулятор как раз создан для того, чтобы решать иррациональное уравнение и автоматом проверить все корни, что избавит от забывчивости.

Видео:Система иррациональных уравнений #2Скачать

Бесплатный онлайн калькулятор иррациональных уравнений

Наш бесплатный решатель позволит решить иррациональное уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в калькуляторе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей группе ВКонтакте: pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Наш искусственный интеллект решает сложные математические задания за секунды.

Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!

Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать

Системы уравнений по-шагам

Видео:Решение систем уравнений второго порядка. 8 класс.Скачать

Результат

Примеры систем уравнений

• Метод Гаусса
• Метод Крамера
• Прямой метод
• Система нелинейных уравнений

Указанные выше примеры содержат также:

• квадратные корни sqrt(x),
  кубические корни cbrt(x)
• тригонометрические функции:
  синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
• показательные функции и экспоненты exp(x)
• обратные тригонометрические функции:
  арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс actan(x)
• натуральные логарифмы ln(x),
  десятичные логарифмы log(x)
• гиперболические функции:
  гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x)
• обратные гиперболические функции:
  asinh(x), acosh(x), atanh(x), actanh(x)
• число Пи pi
• комплексное число i

Правила ввода

Можно делать следующие операции

2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание Действительные числа вводить в виде 7.5, не 7,5

Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:

Видео:Система иррациональных уравнений #3Скачать

Калькулятор систем уравнений

Видео:Решение систем уравнений второй степени. Алгебра, 9 классСкачать

Воспользуйтесь нашим простым онлайн-калькулятором системы уравнений, чтобы решать системы уравнений с пошаговым объяснением.

1. Главная
2. Системы уравнений

Добавьте калькулятор алгебры в закладки вашего браузера

1. Для Windows или Linux — нажмите Ctrl + D .

2. Для MacOS — нажмите Cmd + D .

3. Для iPhone (Safari) — нажмите и удерживайте , затем нажмите Добавить закладку

4. Для Google Chrome : нажмите 3 точки в правом верхнем углу, затем нажмите знак звездочки

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Как пользоваться калькулятором систем уравнений

Шаг 1

Введите проблему с системой уравнений в поле ввода.

Шаг 2

Нажмите Enter на клавиатуре или на стрелку справа от поля ввода.

Шаг 3

Во всплывающем окне выберите нужную операцию. Вы также можете воспользоваться поиском.

Видео:Иррациональные уравнения и их системы. 11 класс.Скачать

Что такое системы уравнений

Система уравнений — это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных. Другими словами, если дано несколько уравнений с одной, двумя или несколькими неизвестными и все эти уравнения (равенства) должны выполняться одновременно, мы называем такую группу уравнений системой. Объедините уравнения в систему, используя фигурную скобку.

Калькулятор алгебры с расширенными функциями. Удобный и простой инженерный калькулятор с богатым арсеналом возможностей для математических расчетов и при этом с приятным и интуитивно понятным интерфейсом.

🔥 Видео

Решение задач с помощью систем уравнений второй степени. Алгебра, 9 классСкачать

Алгебра 9 класс. Графическое решение систем уравненийСкачать

Решение системы уравнений методом ГауссаСкачать

Матричный метод решения систем уравненийСкачать

Решение системы уравнений методом Крамера.Скачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Задание №20. Экзамен ОГЭ. Система уравнений #shortsСкачать

Решение систем уравнений второй степениСкачать

Решение системы линейных уравнений. Подстановка. С дробными выражениями.Скачать