Калькулятор показательных уравнений и неравенств (2 видео)

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Содержание

Калькулятор онлайн. Решение показательных неравенств.
Немного теории.
Показательные неравенства
Калькулятор показательных уравнений и неравенств
Решение показательных уравнений онлайн
🔍 Видео

Видео:Это просто! Как решать Показательные Неравенства?Скачать

Калькулятор онлайн.
Решение показательных неравенств.

Этот математический калькулятор онлайн поможет вам решить показательное неравенство. Программа для решения показательного неравенства не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите показательное неравенство
Решить неравенство

Видео:Показательные уравнения. 11 класс.Скачать

Немного теории.

Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Показательные неравенства

Неравенства вида
( a^x > b ) и ( a^x 0, ; a neq 0, ; b in mathbb )
называют простейшими показательными неравенствами.

Напомним, что решением неравенства называют число (x_0), при подстановке которого в неравенство получается верное числовое неравенство.

Решить неравенство — значит найти все его решения или показать, что их нет.

Случай ( b leqslant 0)

Поскольку ( a^x >0 ) для любого ( x in mathbb ), то при ( b leqslant 0) неравенство ( a^x > b ) верно для любого ( x in mathbb ).
И нет ни одного ( x in mathbb ) для которого было бы верно неравенство ( a^x leqslant b ) при ( b leqslant 0).

Таким образом, если ( b leqslant 0), то множество всех решений неравенства ( a^x > b ) есть интервал ( (-infty; ; +infty) ), а неравенство ( a^x 0)

Если же ( b > 0), то исходные неравенства можно переписать в виде
( a^x > a^c ) и ( a^x 1)

Рассмотрим решение неравенств ( a^x > a^c ) и ( a^x 1)
Так как для такого (a) функция ( y = a^x ) является возрастающей, то для любого числа ( x > c ) верно неравенство ( a^x > a^c ), а для любого числа ( x 0) и ( a > 1) множество всех решений неравенства ( a^x > a^c ) есть интервал ( (c; ; +infty) ), а множество всех решений неравенства ( a^x c ) верно неравенство ( a^x a^c ).
Кроме того, равенство ( a^x = a^c ) справедливо лишь при ( x = c ).

Таким образом, при ( b > 0) и ( 0 a^c ) есть интервал ( (-infty; ; c) ), а множество всех решений неравенства ( a^x 0, то неравенство можно переписать в виде (2x 1, то функция (y = 2^x) возрастающая. Поэтому решением неравенства, являются все x 0, то это неравенство можно переписать в виде
$$ left( fracright)^x log_<frac>5 )
Ответ: ( (log_<frac>5 ; ; +infty) )

ПРИМЕР 3. Решим неравенство ( 2^ + 2^

Видео:Системы показательных уравнений и неравенств. Практика. Видеоуроки 13. Алгебра 10 классСкачать

Калькулятор показательных уравнений и неравенств

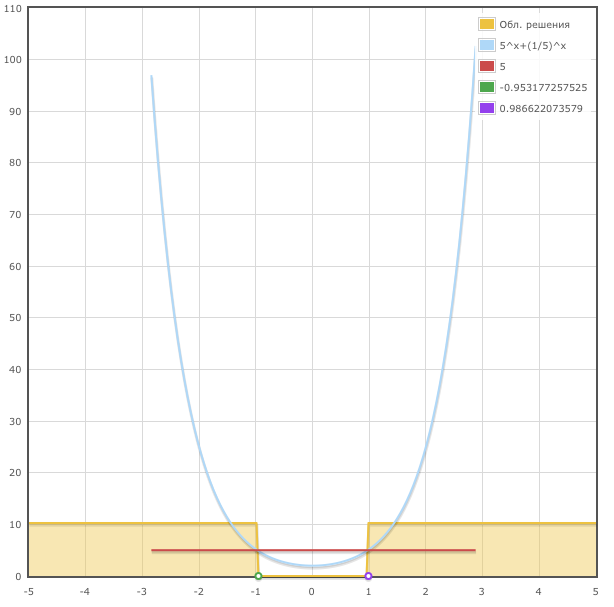
>>решение неравенств онлайн 5$$ Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние: $$5^ + left(fracright)^ = 5$$ Решаем:
Дано уравнение: $$5^ + left(fracright)^ = 5$$ или $$5^ + left(fracright)^ — 5 = 0$$ Сделаем замену $$v = left(fracright)^$$ получим $$v — 5 + frac = 0$$ или $$v — 5 + frac = 0$$ делаем обратную замену $$left(fracright)^ = v$$ или $$x = — frac<log><log>$$ $$x_ = frac<log> left(- log + log <left (sqrt+ 5 right )>right)$$ $$x_ = frac<log> left(log <left (- sqrt+ 5 right )> — logright)$$ $$x_ = frac<log> left(- log + log <left (sqrt+ 5 right )>right)$$ $$x_ = frac<log> left(log <left (- sqrt+ 5 right )> — logright)$$ Данные корни $$x_ = frac<log> left(log <left (- sqrt+ 5 right )> — logright)$$ $$x_ = frac<log> left(- log + log <left (sqrt+ 5 right )>right)$$ являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки: $$x_ 5$$

значит одно из решений нашего неравенства будет при:
$$x frac<log> left(- log + log <left (sqrt+ 5 right )>right)$$

Также вы будете иметь графическое решение показательного неравенства:

Тэги: неравенство

© Контрольная работа РУ — примеры решения задач

Видео:11 класс, 12 урок, Показательные уравненияСкачать

Решение показательных уравнений онлайн

Показательным называется уравнение в котором неизвестная переменная находится в степени, например:

Для решения таких уравнений применяются различные подходы, одним из которых является логарифмирование. Например, прологарифмируем обе части, приведенного выше уравнения:

Приведенный выше пример является простейшим. Наш калькулятор, построенный на системе Wolfram Alpha способен решить практически любые показательные уравнения с подробным решением.