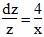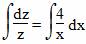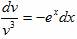Калькулятор линейных уравнений методом бернулли

Назначение сервиса . Онлайн калькулятор можно использовать для проверки решения дифференциальных уравнений Бернулли.

• Решение онлайн
• Видеоинструкция

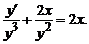
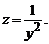
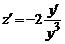
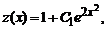
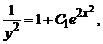
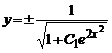
Пример 1 . Найти общее решение уравнения y’ + 2xy = 2xy 3 . Это уравнение Бернулли при n=3. Разделив обе части уравнения на y 3 получаем Делаем замену Тогда и поэтому уравнение переписывается в виде -z’ + 4xz = 4x. Решая это уравнение методом вариации произвольной постоянной, получаем откуда или, что то же самое, .

Пример 2 . y’+y+y 2 =0
y’+y = -y 2

Разделим на y 2
y’/y 2 + 1/y = -1

Делаем замену:
z=1/y n-1 , т.е. z = 1/y 2-1 = 1/y
z = 1/y
z’= -y’/y 2

Получаем: -z’ + z = -1 или z’ — z = 1

Далее надо найти z и выразить через него y = 1/z .

Пример 3 . xy’+2y+x 5 y 3 e x =0
Решение.
а) Решение через уравнение Бернулли.
Представим в виде: xy’+2y=-x 5 y 3 e x . Это уравнение Бернулли при n=3 . Разделив обе части уравнения на y 3 получаем: xy’/y 3 +2/y 2 =-x 5 e x . Делаем замену: z=1/y 2 . Тогда z’=-2/y 3 и поэтому уравнение переписывается в виде: -xz’/2+2z=-x 5 e x . Это неоднородное уравнение. Рассмотрим соответствующее однородное уравнение: -xz’/2+2z=0
1. Решая его, получаем: z’=4z/x

Интегрируя, получаем:
ln(z) = 4ln(z)
z=x 4 . Ищем теперь решение исходного уравнения в виде: y(x) = C(x)x 4 , y'(x) = C(x)’x 4 + C(x)(x 4 )’
-x/2(4C(x) x 3 +C(x)’ x 4 )+2y=-x 5 e x
-C(x)’ x 5 /2 = -x 5 e x или C(x)’ = 2e x . Интегрируя, получаем: C(x) = ∫2e x dx = 2e x +C
Из условия y(x)=C(x)y, получаем: y(x) = C(x)y = x 4 (C+2e x ) или y = Cx 4 +2x 4 e x . Поскольку z=1/y 2 , то получим: 1/y 2 = Cx 4 +2x 4 e x

б) решение через замену переменных
y=uv
x(u’v + uv’)+2uv+x 5 u 3 v 3 e x =0
v(x u’ + 2u) + xuv’+ x 5 u 3 v 3 e x = 0
a) xu’+2u = 0
или ln(u)=ln(x -2 ). Откуда u = x -2
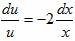
b) xuv’+ x 5 u 3 v 3 e x = 0
x x -2 v’+ x 5 x -6 v 3 e x = 0
v’/x+ v 3 e x /x = 0
v’+ v 3 e x = 0

или 1/y 2 = Cx 4 +2x 4 e x

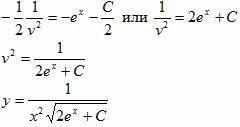
Видео:Уравнение Бернулли Метод БернуллиСкачать

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)

Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Решение дифференциальных уравнений

Данный онлайн калькулятор позволяет вычислять дифференциальные уравнения практически любого типа и порядка: линейные дифференциальные уравнения, с разделяемыми или неразделяемыми переменными, уравнения Бернулли и т.д. При этом у вас есть возможность решать уравнения в общем виде или получить частное решение соответствующее введенным вами начальным (граничным) условиям.

По умолчанию в уравнении функция y является функцией от переменной x. Однако вы можете задать своё обозначение переменной, если напишете, например, y(t) в уравнении, то калькулятор автоматически распознает, что y есть функция от переменной t. С помощью калькулятора вы сможете решать дифференциальные уравнения любой сложности и вида: однородные и неоднородные, линейные или нелинейные, первого порядка или второго и более высоких порядков, уравнения с разделяющимися или не разделяющимися переменными и т.д. Решение диф. уравнения даётся в аналитическом виде, имеет подробное описание. Дифференциальные уравнения очень часто встречаются в физике и математике. Без их вычисления невозможно решать многие задачи (особенно в математической физике).
Одним из этапов решения дифференциальных уравнений является интегрирование функций. Есть стандартные методы решений дифференциальных уравнений. Необходимо привести уравнения к виду с разделяющимися переменными y и x и отдельно проинтегрировать разделенные функции. Чтобы это сделать иногда следует провести определенную замену.

💥 Видео

10. Уравнения БернуллиСкачать

Метод Лагранжа & Метод Бернулли ★ Решение линейных неоднородных дифференциальных уравненийСкачать

Дифференциальные уравнения, 5 урок, Уравнение БернуллиСкачать

9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

Теория вероятностей #8: формула Бернулли и примеры ее использования при решении задачСкачать

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Линейные дифференциальные уравнения (Метод Бернулли)Скачать

Метод БернуллиСкачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Метод Бернулли. Метод ЛагранжаСкачать

Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Математика без Ху!ни. Теория вероятностей. Схема БернуллиСкачать

Метод БернуллиСкачать

Уравнения Бернулли. Дифференциальны уравненияСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Дифференциальные уравнения. Уравнение БернуллиСкачать