Калькулятор для решения уравнения интеграла

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

Видео:HP32sII обзор возможностей: решение уравнений, считаем интеграл, переводим величины...Скачать

Калькулятор Интегралов

Видео:Определенный интеграл. 11 класс.Скачать

Вычисление интегралов онлайн
— по шагам и с графиками!

Калькулятор Интегралов позволяет вычислять интегралы и первообразные функций онлайн — совершенно бесплатно!

Наш Калькулятор позволяет проверить решение Ваших математических заданий. Он поможет вам с решением задачи показывая весь ход решения шаг за шагом. Поддерживаются все виды интегрирования включая специальные функции.

Калькулятор Интегралов поддерживает вычисление определённых и неопределённых (первообразных функций) интегралов включая интегрирование функций с несколькими переменными. Кроме этого Вы можете проверить результат своего решения! Интерактивные графики помогут представить и лучше понять функции интегралов.

Чтобы узнать больше о том как пользоваться Калькулятором Интегралов, загляните в раздел «Справка» или ознакомьтесь с примерами.

Ну что ж, теперь — вперед! Успешного интегрирования!

Введите функцию, которую вы хотите проинтегрировать в Калькулятор Интегралов. Не вводите «f(x) =» часть и дифференциал «dx«! Калькулятор Интегралов сразу показывает математическое выражение в графическом виде, прямо в процессе ввода. Убедитесь, что это выражение соответствует тому, что Вы хотели ввести. Используйте скобки если понадобится, например «a/(b+c)«.

В разделе «Примеры», приведены некоторые из функций которые Калькулятор Интегралов способен вычислять.

После того как Вы закончили вводить вашу функцию, нажмите «=» и Калькулятор Интегралов выдаст результат.

В разделе «Настройки» переменная интегрирования и пределы интегрирования могут быть установлены/изменены. Если пределы интегрирования не будут указаны, то будет вычислена только лишь первообразная функция.

Щелчок мышки на примере вводит его в Калькулятор Интегралов. Простое наведение мышки — показывает текст выражения.

Настройте параметры калькулятора:

Переменная интегрирования:
Верхний предел (до):	+∞
Нижний предел (от):	–∞
Использовать только численное интегрирование?
Упрощать выражения интенсивнее?
Упрощать все корни? (√ x² станет x, а не |x|)
Использовать комплексные числа (ℂ)?
Использовать числа с запятой вместо дробей?

Генератор заданий для тренировки позволяет сгенерировать сколько угодно различных случайных заданий.

Ниже Вы найдете настройки конфигурации и один из предложенных вариантов задания. Вы можете взяться за его решение (тогда оно будет введено в Калькулятор) или сгенерировать новое.

Вычисляем интеграл: Введите Ваш результат:

Следующее выражение будет вычислено:

Загрузка … пожалуйста подождите!
Это займет несколько секунд.

Это не то, что Вы имели ввиду? Используйте скобки! В случае необходимости, выберите переменную и пределы интегрирования в разделе «Настройки«.

Поддержка

Вам помог мой калькулятор? Расскажите своим друзьям об этом Калькуляторе и Вы тоже сможете мне помочь!

Результаты вычислений

Как работает Калькулятор Интегралов

Для тех кому интересны технические подробности, в этой части рассказывается как устроен и работает Калькулятор Интегралов.

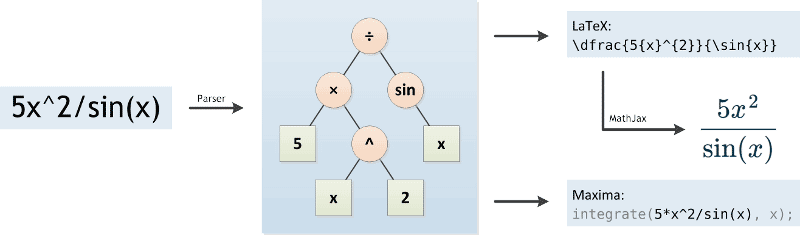
Сначала синтаксический анализатор (па́рсер) анализирует исходное математическое выражение. Он преобразует его в форму более удобную для компьютера, а именно в форму дерева (см. картинку ниже). В процессе такого преобразования, Интегральный Калькулятор должен соблюдать порядок операций с учетом их приоритета. Так же, как и то, что в математических выражениях знак умножения часто опускается, например, мы обычно пишем «5x» вместо «5*x». Калькулятор Интегралов должен уметь понимать такие случаи и сам добавлять знак умножения.

Па́рсер написан на JavaScript, и основывается на алгоритме сортировочной станции, поэтому может исполняться прямо в браузере. Это дает возможность генерировать удобочитаемое выражение на ходу, преобразуя получающееся дерево в код для LaTeX (Ла́тех). С помощью MathJax происходит генерация картинки и ее отображение в браузере.

По нажатию кнопки «=», Калькулятор Интегралов отправляет математическое выражение вместе с параметрами (переменной интегрирования и пределами интегрирования) на сервер, где оно анализируется еще раз. В этот раз выражение преобразуется в форму которая будет понятна системе компьютерной алгебры Maxima (Ма́ксима).

Ма́ксима вычисляет интеграл математической функции. Результат Ма́ксимы снова преобразуется в Ла́тех а затем показывается пользователю. Первообразная вычисляется с помощью алгоритма Ри́ша, который достаточно замысловат для понимания человеком. Именно поэтому задача показывать промежуточные шаги решения интегралов является такой сложной.

Для того чтобы всё-таки показать пошаговое решение, Калькулятор Интегралов использует такие же методы, которыми бы воспользовался человек. Алгоритм, который это осуществляет, разрабатывался в течении нескольких лет и был написан на собственном языке программирования Ма́ксимы. Программа содержит более чем 17000 строк кода. Если интегрируемое выражение совпадает по форме с уже известным, алгоритм применяет заранее определённые правила для решения интеграла (например, метод неопределённых коэффициентов для рациональных функций, тригонометрическую подстановку в интегралах с квадратным корнем из квадратичной функции или интегрирование по частям для продуктов определенных функций). Если же оно не совпадает с уже известным, тогда алгоритм пробует разные подстановки и преобразования пока интеграл не будет решен или пока не закончится отведённое для этого время или же пока не кончатся все возможные варианты. С одной стороны, у Калькулятора нет математической интуиции, которая бы очень помогла в поисках первообразной, но зато, с другой стороны, Калькулятор в состоянии перепробовать большое количество разных вариантов за очень короткое время. Такое пошаговое вычисление первообразной по правилам, зачастую, более компактно и элегантно чем вычисленное Ма́ксимой.

Еще один режим работы «Проверка решения» должен решить сложную задачу по определению являются ли два математических выражения равными друг другу. Разница между выражениями вычисляется и упрощается с помощью Ма́ксимы настолько, насколько это возможно. К примеру, это может быть переписывание тригонометрических/гиперболических функций в их экспоненциальные формы. Если удается упростить разницу до нуля — задача выполнена. В противном случае, применяется вероятностный алгоритм, который вычисляет и сравнивает оба выражения в случайно выбранных местах. В случае с первообразной, вся процедура повторяется для каждой производной, т.к. первообразная может отличаться константой.

Интерактивные графики функций вычисляются в браузере и отрисовываются на Сanvas («Холст») из HTML5. Для каждой математической функции, которая должна быть отрисована, Калькулятор создает функцию JavaScript, которая затем вычисляется с шагом, необходимым для правильного отображения графика. Все сингулярности (например полюса) функции обнаруживаются в процессе отрисовки и обрабатываются отдельно. Управление жестами для мобильных устройств сделано на основе hammer.js.

Если у Вас есть вопросы или пожелания, а так же идеи как улучшить Калькулятор Интегралов, пожалуйста пишите мне на e-mail.

© David Scherfgen 2022 — all rights reserved.

Видео:Математика это не ИсламСкачать

Неопределенный интеграл

Неопределенный интеграл онлайн

В школе говорят, интеграл – это значок ∫, а вычисление интеграла, то есть процесс интегрирования, – это операция обратная дифференцированию. Согласитесь скучно!

Разумеется, у школьников возникает резонный вопрос: а нафиг он нам нужен?

Но если бы учитель уделил несколько минут на вводную про интегралы, такой вопрос всё равно бы возник, но уже не у всех!

Вводная к интегралам

В далеком 17 веке были на тот момент нерешенные насущные проблемы, а именно изучались закономерности движения тел. Много трудов было проделано Ньютоном, чтобы понять, как вычисляется скорость тела в любой момент времени. Но чем дальше, тем оказалось интереснее.

Допустим, мы знаем закон изменения скорости тела – это некая функция. Тогда площадь фигуры, ограниченная этой кривой и осью координат, будет равна пройденному пути. Вычисляя неопределенный интеграл от функции, мы как раз находим общий закон движения.

В этом заключается один из физических смыслов интеграла.

Как вы уже поняли, геометрический смысл интеграла – это площадь криволинейной трапеции. Соответственно с помощью кратного интеграла вычисляется объем тела.

Лейбниц и Ньютон заложили основы дифференциального и интегрального исчисления. В последующие десятилетия было много великих открытий, связанных с вычислением интегралов.

Поскольку подынтегральная функция может принимать различные виды, естественно это привело к разделению интегралов на свои типы, а главное были отрыты многочисленные методы решения интегралов.

Но не все так безоблачно. На практике часто происходит так, что в аналитическом виде вычислить интегралы невозможно, то есть используя какой-либо известный метод. Конечно, получить аналитическое решение это здорово, но, с другой стороны, главное ведь вычислить точное значение интеграла. В этом случае интегралы решаются численными методами. Благодаря компьютерным мощностям, такие задачи не представляют особых сложностей для современного человека.

Калькулятор решения интегралов

Теперь самое интересное. Еще каких-то 15 лет назад школьник и помыслить не мог, что под рукой будут такие калькуляторы интегралов, как, например, наш. Это безусловно облегчает процесс обучения. Можно проверять свои решения, находить допущенные ошибки и лучше усваивать образовательный курс.

И тут в который раз повторяем, калькулятор решения интегралов – это только ваш безотказный помощник, к которому можете обратиться в любое время. Но никак не подмена вашей головы. Старайтесь самостоятельно решать задачи, только так можно развивать мышление, а компьютер будет в помощь.

📺 Видео

ИНТЕГРАЛ С НУЛЯ | определенный интеграл | ТАБЛИЦА ИНТЕГРАЛОВ | сумма РиманаСкачать

Математика без ху!ни. Интегралы, часть 1. Первообразная. Дифференцирование и интегрирование.Скачать

Калькулятор для чайников | Гайд по калькулятору для ЕГЭ по ФизикеСкачать

Гайд на CASIO. Все функции casio.Скачать

Как посчитать любое уравнение! Шок!!Скачать

Обзор инженерного калькулятораСкачать

Программируемые графические калькуляторы! Casio fx-cg50Скачать

Математика без Ху!ни. Определенные интегралы, часть 1.Скачать

Примеры решения определенных интеграловСкачать

Как использовать интеграл в обычной жизни. Математик МГУ и Савватеев #shortsСкачать

Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Определенные и неопределенные интегралы для чайников. Свойства интегралов.Скачать

Функция SOLVE.Обучающее видеоСкачать

Неопределенный интеграл. Примеры решений интегралов. Часть 1 | Высшая математика TutorOnlineСкачать

Видеоурок по математике "Вычисление интегралов - 1"Скачать