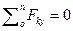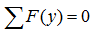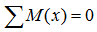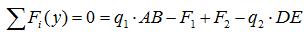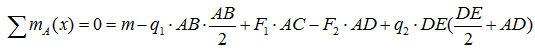Читайте также:
|
| < |  |
 | |
 |
Контрольные вопросы и задания
1. Замените распределенную нагрузку сосредоточенной и определите расстояние от точки приложения равнодействующей до опоры А (рис. 6.9).
2. Рассчитайте величину суммарного момента сил системы относительно точки А (рис. 6.10).
3. Какую из форм уравнений равновесия целесообразно использовать при определение реакций в заделке?
4. Какую форму системы уравнений равновесия целесообразно использовать при определении реакций в опорах двухопорной балки и почему?
5. Определить реактивный момент в заделке одноопорной балки, изображенной на схеме (рис. 6.11).
6. Определите вертикальную реакцию в заделке для балки, представленной на рис. 6.11.
Дата добавления: 2015-04-11 ; просмотров: 16 ; Нарушение авторских прав
Видео:Статика. Условия равновесия плоской системы сил (23)Скачать

Определение опорных реакций балки, нагруженной плоской системой произвольно расположенных сил
Лабораторная работа 3
Цель работы: определение опытным путем реакций связи опор в одноопорной и двухопорной балках и сравнение их с величинами, полученными аналитическим способом.
Краткие теоретические сведения
Система сил, действующих на тело, называется плоской, если все силы лежат в одной плоскости. Если нет дополнительных особенностей расположения сил, то данная система является плоской системой произвольно расположенных сил. Такая система включает силы и моменты пар сил.
По способу приложения силы условно делятся на сосредоточенные и распределенные. Предполагают, что сосредоточенная сила прилагается к точке. Распределенная сила прилагается на участке линейном или поверхностном. Равномерно-распределенная нагрузка изображается в виде прямоугольника, в котором параллельные стрелки указывают, в какую сторону действует нагрузка. Равномерно распределенная нагрузка задается двумя параметрами — интенсивностью q, т. е. числом единиц силы (Н или кН), приходящихся на единицу длины (м), и длиной / (рис. 1.3.1, а).
Равномерно-распределенную нагрузку можно заменить равнодействующей сосредоточенной силой Q, равной Q = ql и приложенной посередине длины / (рис. 1.3.1, б).
Рис. 1.3.1. Равномерно распределенная нагрузка
Рис. 1.3.2. Пара
Система антипараллельных сил, равных по модулю, называются парой сил или просто парой. Расстояние между линиями действия пары есть плечо пары. Эффект действия пары состоит в том, что она стремится вращать тело, к которому приложена. Её вращательное действие определяется моментом пары. Моментом пары называется произведение модуля одной из пар сил, составляющих пару, на плечо (рис. 1.3.2):
Условимся считать момент пары положительным, если она стремится вращать свое плечо против часовой стрелки, и наоборот.
Пара сил не имеет равнодействующей, она не может быть уравновешена одной силой, а только парой сил.
Момент пары сил относительно любой точки плоскости её действия есть величина постоянная.
Алгебраическая сумма проекций сил пары на ось всегда равна нулю. Пара сил не входит ни в уравнение сил, ни в уравнение проекции сил.
Объектом решения многих задач статики служат балки или балочные системы. Балкой называется конструктивная деталь какого-либо сооружения, выполняемая в большинстве случаев в виде прямого бруса с опорами в двух (или более) точках.
Опоры и опорные реакции балок. Опоры балок по их устройству могут быть разделены на три основных типа (рис. 1.3.3):
- 1) шарнирно-подвижная (опора А);
- 2) шарнирно-неподвижная (опора В);
- 3) жесткая заделка (опора Q.
Рис. 1.3.3. Опоры
Шарнирно-подвижная (опора А) допускает поворот вокруг оси шарнира и линейное перемещение параллельно опорной плоскости. Если пренебречь трением на опоре и в шарнире, то реакция такой связи будет направлена перпендикулярно опорной плоскости и не известна только по модулю (одно неизвестное).
Шарнирно-неподвижная (опора В) допускает только поворот вокруг оси шарнира и не допускает никаких линейных перемещений. Реакция такой опоры будет направлена перпендикулярно оси шарнира, модуль и направление её заранее не известны (два неизвестных). Обычно такую реакцию раскладывают на две взаимно перпендикулярные составляющие, не известные по модулю, но известные по направлению (рис. 1.3.3).
Жесткая заделка (защемление) не допускает ни линейных перемещений, ни поворотов защемленного конца балки. Жесткую заделку заменяют реактивной силой, не известной по модулю и направлению, и реактивным моментом (три неизвестных). Реактивную силу раскладывают на две взаимно перпендикулярные составляющие.
Если при определении реакций они получаются отрицательными, то их действительное направление противоположно принятому.
Условия равновесия плоской системы произвольно расположенных сил. Для равновесия плоской системы необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на оси координат X и Y равнялись нулю и чтобы алгебраическая сумма моментов этих сил относительно любой точки плоскости также равнялась нулю.
Условия равновесия запишем в виде равенств:
Существуют три формы условий равновесия.
Первая форма условий равновесия: записываются два уравнения суммы проекций сил на две координатные оси (X и Z) и одно уравнение суммы моментов сил относительно точки.
Первую форму условий равновесия целесообразно использовать для консольной балки (рис. 1.3.4, а):
Вторая форма условий равновесия: записываются одно уравнение суммы проекций сил на ось Z и уравнения суммы моментов сил относительно двух точек. Как правило, это точки опор А и В (рис. 1.3.4, б):
Рис. 1.3.4. Балки
Третья форма условий равновесия: записываются три уравнения суммы моментов сил относительно точек, не лежащих на одной прямой.
Приборы и принадлежности: лабораторная установка ТМт 03М, измерительные индикаторы часового типа, тарированные грузы.
Работа проводится на лабораторной установке ТМт 03М (рис. 1.3.5), которая состоит из основания 1 с двумя опорными стойками 2, на которых установлена стальная балка 3 трубчатого сечения или зажатая на левой опоре консольная балка. Закрепленные на пружинящих корпусах 4 измерительные индикаторы часового типа 5 позволяют определять модули горизонтальных и вертикальных составляющих опорных реакций с погрешностью не более 5 %.
Рис. 1.3.5. Схема установки
Равномерно распределенная нагрузка на балку создается посредством набора стальных брусков 10, свободно устанавливаемых сверху. Нагружение балки сосредоченными силами осуществляется при помощи грузов 6 и 8, подвешиваемых на нитях, концы которых прикреплены к подвижным ползунам 9, которые можно передвигать вдоль балки. Одна из нитей, на которую подвешивается груз 8, может отклоняться от вертикали роликом 11, установленным на конце штанги штатива 12, закрепленного на основании 1. Штанга с роликом может перемещаться по вертикали и фиксируется винтом.
Для приложения к балке пары сил служит двуплечий рычаг 7, на концах которого также установлены ролики, охватываемые нитью 13. Один конец этой нити крепится к стойке 72, а к другому концу подвешивается груз 14, сила тяжести которого равна каждой из двух сил пары, нагружающей балку. Серьги 15 служат для подвешивания грузов и регулировки длин нитей.
Порядок выполнения работы
- 1. Задать нагрузку: сосредоточенные силы F и F2 (до 40 Н), изгибающий момент М (до 2 Н/м), распределенную нагрузку q (200 Н/м).
- 2. Ознакомиться с устройством лабораторной установки и работой на ней.
- 3. Разместить установку на ровной горизонтальной поверхности стола.
- 4. Собрать установку с одной из двух исследуемых балок (с консольным защемлением, балка на двух опорах).
- 5. Построить тарировочный график зависимости показаний датчиков от силы, приложенной посередине балки, каждый раз увеличивая силу и снимая показания датчиков.
- 6. Произвести нагружение балки заданными силами 7д, F2, моментом М и нагрузкой q.
- 7. Снять показания измерительных индикаторов.
- 8. Перевести показания измерительных индикаторов в силу по тари- ровочному графику (RA,HA,R 3 B).
- 9. Построить расчетную схему балки с приложенными нагрузками (рис. 1.3.6).
- 10. Определить реакции связей аналитическим методом, используя одну из форм условий равновесия (RA, НА,Rl).
- 11. Свести результаты расчетов и измерений в таблицу.
Рис. 1.3.6. Расчетная схема
12. Сравнить практические данные с расчетными, определить погрешность
Контрольные вопросы и задания
- 1. Назовите различные виды опор.
- 2. Какие реакции возникают со стороны каждой из этих видов опор?
- 3. Какие виды нагрузок вы знаете?
- 4. Назовите условие равновесия плоской системы произвольно расположенных сил.
- 5. Какие формы условий равновесия вы знаете?
- 6. В каких случаях рекомендуется та или иная форма условий равновесия?
- 1. Построенный тарировочный график.
- 2. Заданная система произвольно расположенных сил:
3. Реакции опор на лабораторной установке:
- 4. Расчетная схема балки.
- 5. Реакции опор теоретическим методом:
6. Таблица результатов, полученных экспериментальным и теоретическим методами (табл. 1.3.1).
Видео:Три формы уравнений равновесия произвольной плоской системы силСкачать

iSopromat.ru
Для плоской системы нагружения, при определении опорных реакций и внутренних силовых факторов исходя из условия равновесия системы, можно составить только три уравнения статики.
Ранее были показаны примеры составления уравнений равновесия для пространственной и плоской систем сил.
При плоском поперечном изгибе можно записать только два уравнения. Это частный случай плоского нагружения. В этом случае все силы приложенные к балке расположены нормально к ее оси, т. е. не дают проекций на ось балки.
В результате имеем следующие уравнения статики:
- Сумма проекций всех сил на вертикальную ось равна нулю
- Сумма моментов относительно любой точки системы тоже равна нулю.
Эти уравнения являются уравнениями равновесия рассматриваемой балки находящейся под действием комплекса нагрузок.
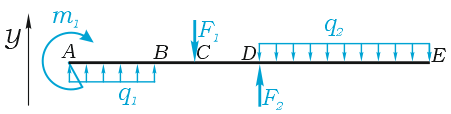
Рассмотрим пример плоского поперечного изгиба, когда все внешние силы имеют исключительно вертикальное направление.
Видео:Определение реакций опор простой рамыСкачать

Уравнения статики
Сумма проекций всех сил на ось Y:
Здесь силы и нагрузки записаны в соответствии с правилом знаков для проекций сил.
Равнодействующая распределенной нагрузки определяется произведением ее интенсивности на длину.
Проекции сил на ось Z в данном случае равны нулю:
Сумма моментов всех нагрузок, например, относительно точки A :
Видео:Задача о составной конструкцииСкачать

Дополнительные материалы
- Порядок определения момента от распределенной нагрузки.
- Правила знаков при составлении уравнений статики для систем находящихся в равновесии.
Совместное решение системы полученных уравнений позволяет определить величину и направление двух неизвестных усилий.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Видео:Как выучить Химию с нуля за 10 минут? Принцип Ле-ШательеСкачать

Решение задач, контрольных и РГР
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ
— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку
🎬 Видео
Практическая работа №3 Нахождение реакций в заделкеСкачать

Основы Сопромата. Виды опор. Определение реакций опорСкачать

Видеоурок 2. Определение реакций двухопорных балок.Скачать

Метод сеченийСкачать

Сопротивление материалов/ Изгиб. Определение опорных реакций, построение эпюр Q и M. (Перезапись)Скачать

Расчет составных конструкцийСкачать

Термех. Статика. Расчётно-графическая работа по статике №2. Задание 1 и решениеСкачать

Урок 78. Решение задач статики (часть 2)Скачать

Статически неопределимые системы. Метод силСкачать

Составная рама с распределенной нагрузкойСкачать

Симметричные системы #1Скачать

Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать

Условия смещения химического равновесия. 9 класс.Скачать

ЗАПОМНИ ТРИ ГЛАВНЫХ ПРАВИЛА и ты сможешь удивить своего препода по сопромату!Скачать

2.3. Равновесие плоской системы параллельных сил (1 из 2)Скачать





 Рис. 6.2
Рис. 6.2

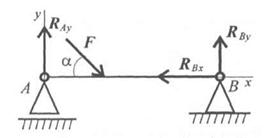

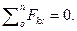
 определяется реакция RBx.
определяется реакция RBx. определяется реакция RBy.
определяется реакция RBy. определяется реакция RAy.
определяется реакция RAy.