Читайте также:
|
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 |


1. Каков физический смысл момента инерции материальной точки, твердого тела?
2. Как вычислить момент инерции тела относительно оси, проходящей через центр масс?
3. Сформулировать теорему Штейнера.
4. получить связь между максимальной угловой скоростью стержня и амплитудой его колебаний.
5. Получить формулу для расчета момента инерции шара, кольца, стержня относительно оси, проходящей через центр масс.
1.Савельев общей физики. т.1. М:Наука, 1986.- гл. V, §39, 41, гл. VII, §54.
Лабораторная работа №6
Видео:Урок 327. Гармонические колебанияСкачать

Определение радиуса кривизны вогнутой поверхности
методом катающегося шарика
Цель работы: изучить законы движения катающегося по сферической вогнутой поверхности шарика, рассмотреть условия его гармонических колебаний и определить радиус кривизны поверхности

Если пренебречь потерями энергии, затрачиваемой на преодоление диссипативной силы трения, то для катающегося без проскальзывания шарика должен выполняться закон сохранения механической энергии. Центр масс C шарика движется поступательно, но, кроме того, шарик вращается относительно оси z, проходящей через точку C перпендикулярно плоскости (рис.1). Поэтому полная механическая энергия шарика

Здесь m – масса шарика; 
Модуль угловой скорости w шарика вокруг оси z связан с модулем скорости Vc поступательного движения центра масс соотношением

Подставляя (2) и выражение для Jc в (1), получаем

Но при качении шарика по сферической поверхности его центр масс отклоняется относительно центра O поверхности на угол j. Из рис.1 видно, что угол j связан с углом поворота q шарика относительно оси z соотношением

где 

Подставляя (4) и (5) в формулу (3), выражаем полную механическую энергию шарика через угол j:

В верхней точке траектории скорость шарика равна нулю и вся механическая энергия шарика переходит в потенциальную. При прохождении шариком положения равновесия (h=0) скорость и кинетическая энергия шарика максимальны.
Рассмотрим кинематику движения шарика. Скорость 





Ускорение 

Эти модули изменяются при колебательных движениях шарика периодически. В верхней точке траектории при наибольшем отклонении шарика от положения равновесия Vc шарика и an равны нулю, а ar достигает максимума. При прохождении положения равновесия, наоборот, 
Найдем период колебаний шарика. Для этого необходимо получить динамическое уравнение колебаний (т. е. уравнение динамики для поступательного или вращательного движения колеблющегося шарика).Для любых незатухающих гармонических колебаний это уравнение имеет общий вид

Физическое тело будет совершать гармонические колебания в том случае, если на него действует сила или момент силы, пропорциональные смещению от положения равновесия и стремящиеся вернуть тело в положение равновесия.
Воспользуемся законом сохранения механической энергии (6). Возьмем производную по времени от обеих частей этого уравнения, сократим полученное выражение на 

Отсюда видно, что шарик будет совершать гармонические колебания относительно положения равновесия в том случае, когда 
В этом случае угол j изменяется по гармоническому закону 

Используя выражения (4), (7) и (8), можно вычислить значения скорости и ускорения шарика в любой момент времени. Чтобы найти зависимость радиуса кривизны R сферической поверхности от периода T, которую находим из формулы (11), подставим в нее 

При вычислении мы не учитывали, что механическая энергия шарика уменьшается за счет работы диссипативной силы трения и потому в действительности колебания шарика будут затухающими. Затуханием колебаний в работе пренебрегаем.
Закон сохранения полной механической энергии
Полная механическая энергия консервативной системы, находящейся в стационарном потенциальном поле, постоянна:
где Uсоб – собственная потенциальная энергия системы – это энергия взаимодействия друг с другом всех частиц системы. Она зависит от взаимного расположения частиц системы; Uвнеш – внешняя потенциальная энергия системы – это сумма потенциальных энергий всех ее частиц, находящихся во внешнем стационарном потенциальном поле; K – кинетическая энергия системы – это сумма кинетических энергий составляющих ее частиц.
Если работа сил стационарного поля над частицей не зависит от пути, пройденного частицей, а зависит только от начального и конечного положения частицы, то такие силы называются консервативными, а поле потенциальным.
1. С помощью микрометра 5 раз в разных местах измерить диаметр шарика d и вычислить радиус r = d/2.
2. Вывести шарик из положения равновесия так, чтобы угол отклонения j (см. рис.1) был мал. Определить время t пяти (n=5) полных колебаний шарика. Опыт провести 9 раз. Определить период колебаний 
3.Вычислить средние значения радиуса шарика и периода колебаний 
4. Определить случайные отклонения 



5. Подставляя 

6. Найти абсолютную ∆R и относительную E погрешности в определении R по формулам


Данные измерений и вычислений занести в табл. 1-3.
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Механические колебания
теория по физике 🧲 колебания и волны
Колебательное движение очень распространено. Заставить колебаться можно любое тело, если приложить к нему силу — однократно или постоянно. К примеру, если подтолкнуть качели, они начнут качаться вперед-назад, и такое движение будет приблизительно повторяться до тех пор, пока качели полностью не остановятся.
Другой пример колебательного движения — тело, подвешенное к пружине. Если его потянуть вниз и отпустить, то за счет сил упругости оно сначала поднимется вверх, а затем снова опустится вниз, затем движения вверх-вниз будут повторяться. Со временем они прекратятся под действием силы сопротивления воздуха.
Колебаниями можно назвать даже движение гири, которую поднимается тяжелоатлет вверх, а затем опускает в низ. При этом он будет прикладывать к гире силу постоянно. Гиря будет колебаться до тех пор, пока к нему будет прикладываться эта сила.
Колебания — это движения, которые точно или приблизительно повторяются через определенные интервалы времени.
Механические колебания — это колебательные движения, совершаемые физическим телом в механической системе.
Механическая система — совокупность материальных точек (тел), движения которых взаимосвязаны между собой.
Видео:Виды КОЛЕБАНИЙ | ЕГЭ Физика | Николай НьютонСкачать

Какими бывают колебания?
Напомним, что в механической системе выделяют два вида сил:
- Внутренние силы — это силы, которые возникают между телами внутри системы. Примером внутренних сил служат силы тяготения между телами солнечной системы.
- Внешние силы — силы, которые действуют на тела системы со стороны тел, которые в эту систему не входят. Примером внешней силы может стать сила ветра, под действием которой шарик, подвешенный к опоре за нить, отклоняется в сторону порыва ветра.
Свободные колебания
Свободные колебания — колебания, происходящие в системе под действием внутренних сил после того, как эта система выведена из положения равновесия.
Колебательная система — механическая система, в которой возможно совершение свободных колебаний.
Свободные колебания в колебательной системе могут возникнуть только при наличии двух условий:
- После выведения из равновесия в колебательной системе появляются силы, направленные в сторону положения равновесия. Эти силы стремятся возвратить систему в положение равновесия.
- Трение между телами колебательной системы относительно мало. В противном случае колебания либо сразу затухнут, либо не начнутся совсем.
Примеры свободных колебаний:
- колебания шарика на дне сферической чаши;
- движение качелей после однократного толчка;
- колебания груза на пружине после ее растяжения;
- колебания струны после ее отклонения.
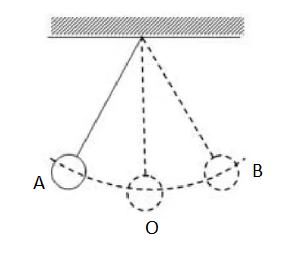
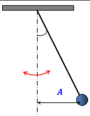
Примером колебательной системы также служит математический маятник — материальная точка, подвешенная на невесомой нерастяжимой нити. В действительности такого маятника не существует. Это идеализированная модель реального маятника, примером которого служит тяжелый шарик, подвешенный на длинной нити. В этом случае размером шарика и растяжением нити можно пренебречь.
В колебательную систему математического маятника входят:
- нить;
- тело, привязанное к нити;
- Земля, в поле тяжести которой находится привязанное к нити тело.
В положении равновесия (точка О) шарик висит на нити и покоится. Если его отклонить от положения равновесия до точки А и отпустить, под действием силы тяжести шарик приблизится к положению равновесия. Так как к этому моменту шарик обретет скорость, он не сможет остановиться и приблизится к точке В. Затем он снова вернется в точку А через положение равновесия в точке О. Шарик будет колебаться, пока не затухнут под действием возникающей силы сопротивления воздуха.
Вынужденные колебания
Вынужденные колебания — колебания тел под действием внешних периодически изменяющихся сил.
Примерами вынужденных колебаний служат:
- движение поршня в цилиндре;
- раскачивание ветки дерева на ветру;
- движение иглы швейной машинки;
- движение качелей под действием постоянных толчков.
Затухающие и незатухающие колебания
Затухающие колебания — колебания, которые со временем затухают. При этом максимальное отклонение тела от положения равновесия с течением времени уменьшается.
Колебания затухают под действием сил, препятствующих колебательному движению. Так, шарик в сферической чаше перестает колебаться под действием силы трения. Математический маятник и качели перестают совершать колебательные движения за счет силы сопротивления воздуха.
Все свободные колебания являются затухающими, так как всегда присутствует трение или сопротивление среды.
Незатухающими колебаниями могут быть только те, которые совершаются под действием периодической внешней силы (вынужденные колебания). Так, ветка будет раскачиваться до тех пор, пока дует ветер. Когда он перестанет дуть, колебания ветки со временем затухнут. Иголка швейной машинки будет совершать колебательные движения до тех пор, пока швея вращает ручку привода. Когда она перестанет это делать, иголка сразу остановится.
Видео:Физика 9 класс. §25 Гармонические колебанияСкачать

Динамика колебательного движения
Для того чтобы описать количественно колебания тела пол действием силы упругости пружины или колебания шарика, подвешенного на нити, воспользуемся законами механики Ньютона.
Уравнение движения тела, колеблющегося под действием сил упругости
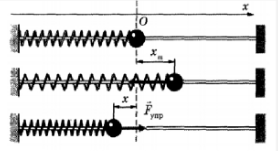
Рассмотрим колебательное движение шарика, вызванное силой упругости, возникшей при растяжении горизонтальной пружины вдоль оси Ох.
Согласно II закону Ньютона произведение массы тела на ускорение равно равнодействующей всех сил приложенных к телу. Поскольку сила трения пренебрежимо мала, мы можем считать, что в этой механической системе действует единственная сила — сила упругости. Учтем, что шарик колеблется вдоль одной прямой, и выберем одномерную систему координат Ох. Тогда:
m a x = F x у п р
Согласно закону Гука, проекция сила упругости прямо пропорциональная смещению шарика из положения равновесия (точки О). Смещение равно координате x шарика, причем проекция силы и координаты имеют разные знаки. Это связано с тем, что сила упругости всегда направлена к точке равновесия, в то время как расстояние от этой точки во время движения увеличивается в обратную сторону. Отсюда делаем вывод, что сила упругости равна:
F x у п р = − k x
где k — жесткость пружины.
Тогда уравнение движения шарики принимает
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Так как масса шарики и жесткость пружины для данной колебательной системы постоянны, отношение k m . . — постоянная величина. Отсюда делаем вывод, что проекция a x ускорения тела прямо пропорциональна его координате x, взятой с противоположным знаком.
Пример №1. Груз массой 0,1 кг прикрепили к пружине школьного динамометра жесткостью 40 Н/м. В начальный момент времени пружина не деформирована. После того, как груз отпускают, возникают колебания. Чему равна максимальная скорость груза?
Максимальной скорости груз достигнет при максимальном его отклонении от положения равновесия — в нижней точке траектории. Учтем, что тело движется вниз под действием силы тяжести. Но в то же время на него действует сила упругости, которая возникает в пружине и нарастает до тех пор, пока не становится равной по модулю силе тяжести. Применив III закон Ньютона получим:
∣ ∣ ∣ → F т я ж ∣ ∣ ∣ = ∣ ∣ ∣ → F у п р ∣ ∣ ∣
где y m a x — максимальное отклонение груза от положения равновесия. В этой точке скорость тела будет максимальная. Для нахождения этой величины используем формулу из кинематики:
y m a x = v 2 m a x − v 2 0 2 g . .
Начальная скорость равна нулю. Отсюда:
y m a x = v 2 m a x 2 g . .
m g = k v 2 m a x 2 g . .
Максимальная скорость равна:
v m a x = g √ 2 m k . . = 10 √ 2 · 0 , 1 40 . . ≈ 0 , 71 ( м с . . )
Уравнение движения математического маятника
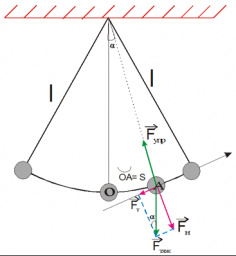
Ниже на рисунке представлен математический маятник. Если мы выведем из положения равновесия шарик и отпустим, возникнет две силы:
- сила тяжести, направленная вниз;
- сила упругости, направленная вдоль нити.
При колебаниях шарика также будет возникать сила сопротивления воздуха. Но так как она очень мала, мы будем ею пренебрегать.
Чтобы описать динамику движения математического маятника, удобно силу тяжести разложить на две составляющие:
→ F т = → F τ + → F n
Причем компонента → F τ направлена перпендикулярно нити, а → F n — вдоль нее.
Компонента → F τ представляет собой проекцию силы тяжести в момент, когда нить маятника отклонена от положения равновесия (точки О) на угол α. Следовательно, она равна:
→ F τ = − → F т sin . α = − m g sin . α
Знак «–» мы здесь поставили по той причине, что компоненты силы тяжести → F τ и α имеют противоположные знаки. Ведь если отклонить шарик на угол α>0, то составляющая → F τ будет направлена в противоположную сторону, так как она будет пытаться вернуть шарик в положение равновесия. И ее проекция будет отрицательной. Если же шарик отклонить на угол α → F τ будет направлена в обратную сторону. В этом случае ее проекция будет положительной.
Обозначим проекцию ускорения маятника на касательную к его траектории через a τ . Эта проекция характеризует быстроту изменения модуля скорости маятника. Согласно II закону Ньютона:
m a τ = − m g sin . α
Разделим обе части выражения на массу шарика m и получим:
При малом отклонении нити маятника от вертикали можно считать, что sin . α ≈ α (при условии, что угол измерен в радианах). Тогда:
Внимание! Чтобы перевести градусы в радианы, нужно умножить градусы на число π и поделить результат на 180. К примеру 2 о = 2∙3,14/180 рад., или 2 о = 0,035 рад.
При малом отклонении также дугу ОА мы можем принять за длину отрезка OA, который мы примем за s. Тогда угол α будет равен отношению противолежащего катета (отрезка s) к гипотенузе (длине нити l):
Так как ускорение свободного падения и длина нити для данной колебательной системы постоянны, то отношение g l . . — тоже постоянная величина.
Это уравнение похоже на то уравнение, которое мы получили для описания колебательного движения шарика под действием силы упругости. И оно также позволяет сделать вывод, что ускорение прямо пропорционально координате.
Пример №2. Определить длину нити, если шарик, подвешенный к ней, отклонится на 1 см. При этом нить образовала с вертикалью угол, равный 1,5 о .
При отклонениях на малый угол мы можем пользоваться следующей формулой:
Чтобы найти длину нити, нужно выразить угол α в радианах:
1 , 5 ° = 3 , 14 · 1 , 5 180 . . ≈ 0 , 026 ( р а д )
Тогда длина нити равна:
l = s α . . = 0 , 01 0 , 026 . . ≈ 0 , 385 ( м ) = 38 , 5 ( с м )
Видео:Гармонические колебания | Физика 9 класс #25 | ИнфоурокСкачать

Основные характеристики колебательного движения
Амплитуда — максимальное отклонение тела от положения равновесия. Обозначается буквой A, иногда — xmax. Единиц измерения — метр (м).
Период — время совершения одного полного колебания. Обозначается буквой T. Единица измерения — секунда (с).
Частота — количество колебаний, совершенных в единицу времени. Обозначается как ν («ню»). Единица измерения — 1/секунда, или секунда –1 , или герц (1/с, или с –1 , или Гц).
Период и частота колебаний связаны между собой следующей формулой:
Период колебаний также можно вычислить, зная количество совершенных колебаний N за время t:
Поскольку частота — это величина, обратная периоду колебаний, ее можно выразить в виде:
Пример №3. Определить частоту колебаний груза, если суммарный путь, который он прошел за 2 секунды под действием силы упругости, составил 1 м. Амплитуда колебаний равна 10 см.
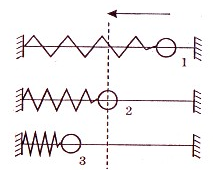
Во время одного колебания груз проходит расстояние, равное 4 амплитудам. Посмотрите на рисунок. Положение равновесия соответствует состояние 2. Чтобы совершить одно полное колебание, сначала груз отводят в положение 1. Когда его отпускают, он проходит путь 1–2 и достигает положения равновесия. Этот путь равен амплитуде колебаний. Затем он продолжает движение до состояния 3. И в это время он проходит расстояние 2–3, равное еще одной амплитуде колебаний. Чтобы вернуться в исходное положение (состояние 1), нужно снова проделать путь в обратном направлении: сначала 3–2, затем 2–1.
Следовательно, количество колебаний равно отношению пройденного пути к амплитуде, помноженной на 4:
Так как мы знаем, что эти колебания совершались в течение 2 секунд, для вычисления частоты мы можем использовать формулу:
ν = N t . . = s 4 A t . . = 1 4 · 0 , 1 · 2 . . = 1 , 25 ( Г ц )
В таблице представлены данные о положении шарика, колеблющегося вдоль оси Ох, в различные моменты времени.
Каков период колебаний шарика?
Алгоритм решения
Решение
Из таблицы видно, что амплитуда колебаний равна 15 мм. Следовательно, максимальное отклонение в противоположную сторону составляет –15 мм. Расстояние между двумя максимальными отклонениями от положения равновесия шарика равно половине периода колебаний. Этим значения в таблице соответствует время 1 и 3 секунды соответственно. Следовательно, разница между ними — половина периода. Тогда период будет равен удвоенной разнице во времени:
T = 2 ( t 2 − t 1 ) = 2 ( 3 − 1 ) = 4 ( с )
pазбирался: Алиса Никитина | обсудить разбор | оценить
Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания. Пружина всё время остается растянутой. Как ведут себя потенциальная энергия пружины, кинетическая энергия груза, его потенциальная энергия в поле тяжести, когда груз движется вверх к положению равновесия?
Для каждой величины определите соответствующий характер изменения:
| 1) | увеличивается |
| 2) | уменьшается |
| 3) | не изменяется |
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
Решение
Потенциальная энергия пружины определяется формулой:
где k — коэффициент жесткости пружины, а x — ее удлинение. Величина x была максимальной в нижней точке траектории. Когда пружина начинает сжиматься, она уменьшается. Так как потенциальная энергия зависит от квадрата x прямо пропорционально, то при уменьшении этой величины потенциальная энергия пружины тоже уменьшается.
Кинетическая энергия тела определяется формулой:
В нижней точке траектории скорость шарика была равна нулю. Но к этому времени потенциальная энергия пружины достигла максимума. Она начинает с ускорением поднимать шарик вверх, сжимаясь. Следовательно, скорость растет. Так как кинетическая энергия зависит от квадрата скорости тела прямо пропорционально, то при увеличении скорости этой величины кинетическая энергия шарика тоже увеличивается.
Потенциальная энергия тел в поле тяжести земли определяется формулой:
Масса и ускорение свободного падения шарика — постоянные величины. Следовательно, потенциальная энергия зависит только от расстояния до поверхности земли. Когда пружина поднимает шарик, расстояние между ним и землей увеличивается. Так как потенциальная энергия зависит от расстояния прямо пропорционально, то при его увеличении потенциальная энергия шарика тоже растет.
pазбирался: Алиса Никитина | обсудить разбор | оценить
В таблице представлены данные о положении шарика, прикреплённого к пружине и колеблющегося вдоль горизонтальной оси Ох, в различные моменты времени.
Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
А) Потенциальная энергия пружины в момент времени 1,0 с максимальна.
Б) Период колебаний шарика равен 4,0 с.
В) Кинетическая энергия шарика в момент времени 2,0 с минимальна.
Г) Амплитуда колебаний шарика равна 30 мм.
Д) Полная механическая энергия маятника, состоящего из шарика и пружины, в момент времени 3,0 с минимальна.
Алгоритм решения
- Проверить истинность каждого утверждения.
- Выбрать 2 верных утверждения.
Решение
Согласно утверждению «А», потенциальная энергия пружины в момент времени 1,0 с максимальна. Потенциальная энергия пружины максимальна, когда она отклоняется от положения равновесия на максимальную возможную величину. Из таблицы видно, что в данный момент времени ее отклонение составило 15 мм, что соответствует амплитуде колебаний (наибольшему отклонению от положения равновесия). Следовательно, утверждение «А» — верно.
Согласно утверждению «Б», период колебаний шарика равен 4,0 с. Один период колебаний включает в себя 4 фазы. В течение каждой фазы шарик на пружине проделывает путь, равный амплитуде. Следовательно, мы можем найти период колебаний, умножив время одной фазы на 4. В момент времени t = 0 с, шарик находился в положении равновесия. Первый раз он отклонился на максимальную величину (15 мм) в момент времени t = 1,0 с. Значит, период колебаний равен 1∙4 = 4 с. Следовательно, утверждение «Б» — верно.
Согласно утверждению «В», кинетическая энергия шарика в момент времени 2,0 с минимальна. В этот момент времени, согласно данным таблицы, шарик проходит положение равновесия. В этом положении скорость шарика всегда максимальна. Поэтому кинетическая энергия, которая зависит от квадрата скорости прямо пропорционально, минимальной быть не может. Следовательно, утверждение «В» — неверно.
Согласно утверждению «Г», амплитуда колебаний шарика равна 30 мм. Амплитуда колебаний — есть расстояние от положения равновесия до точки максимального отклонения шарика. В данном случае оно равно 15 мм. Следовательно, утверждение «Г» — неверно.
Согласно утверждению «Д», полная механическая энергия маятника, состоящего из шарика и пружины, в момент времени 3,0 с минимальна. Полная механическая энергия колебательной системы — это совокупность кинетической и потенциальной энергий. И при отсутствии сил трения она остается величиной постоянной. Она лишь превращается из одного вида энергии в другую. Следовательно, утверждение «Д» — неверно.
pазбирался: Алиса Никитина | обсудить разбор | оценить
📺 Видео
5.4 Уравнение гармонических колебанийСкачать

Математические и пружинные маятники. 11 класс.Скачать

Гармонические колебанияСкачать

Урок 333. "Энергетический" метод расчета частоты свободных колебанийСкачать

Как решить уравнение колебаний? | Олимпиадная физика, механические гармонические колебания, 11 классСкачать

Механические колебания. Как найти период колебаний? | ЕГЭ 2023 по физикеСкачать

математический маятник ЕГЭ ФИЗИКА колебания частота периодСкачать

Гармонические колебания | Физика 11 класс #8 | ИнфоурокСкачать

Лекция №11 "Колебания" (Булыгин В.С.)Скачать

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫСкачать

Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

График гармонического колебания | Алгебра 10 класс #23 | ИнфоурокСкачать

Выполнялка 53.Гармонические колебания.Скачать

10 класс, 19 урок, График гармонического колебанияСкачать

 , (1.3.63)
, (1.3.63) .
. ,
, ,
,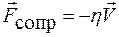 , то уравнение движения системы будет иметь вид:
, то уравнение движения системы будет иметь вид: .
.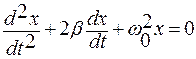 . (1.3.67)
. (1.3.67)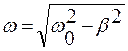 . (1.3.69)
. (1.3.69) . (1.3.71)
. (1.3.71) .
. x
x
 A0
A0 t
t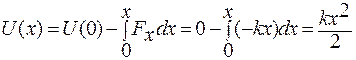 (1.3.72)
(1.3.72)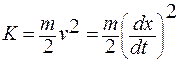 .
.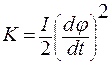 .
.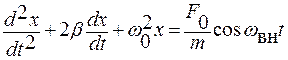 , (1.3.74)
, (1.3.74) ;
; .
. . (1.3.75)
. (1.3.75)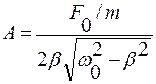 .
. , (1.3.77)
, (1.3.77)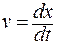 = – 0,5×6,5×sin(6,5t). (1.3.78)
= – 0,5×6,5×sin(6,5t). (1.3.78) = (w0× m× x 2 )/2 = 0,54 (Дж).
= (w0× m× x 2 )/2 = 0,54 (Дж).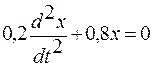 . Найти собственную частоту и период этих колебаний.
. Найти собственную частоту и период этих колебаний. , откуда w0 2 = 4, w0 = 2 (с –1 ).
, откуда w0 2 = 4, w0 = 2 (с –1 ). (с).
(с). . Найти коэффициент затухания и собственную частоту этих колебаний.
. Найти коэффициент затухания и собственную частоту этих колебаний. , откуда видно, что 2b = 0,5 и b = 0,25 (с –1 ).
, откуда видно, что 2b = 0,5 и b = 0,25 (с –1 ). . Найти частоту внешней вынуждающей силы, собственную частоту незатухающих колебаний и резонансную частоту.
. Найти частоту внешней вынуждающей силы, собственную частоту незатухающих колебаний и резонансную частоту. ,
,