Какой способ решения полного квадратного уравнения используется на практике чаще других

Главная
• Список секций
• Математика
• Основные способы решения полных квадратных уравнений

Видео:7. Квадратные уравнения. Другие способы решенияСкачать

Основные способы решения полных квадратных уравнений

Автор работы награжден дипломом победителя III степени

Актуальность выбранной темы продиктована желанием показать разнообразие способов решения квадратных уравнений. Необходимость решать уравнения первой, но и второй степени ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площади земельного участка и с земляными работами военного характера, а также с развитием астрономии и самой математики.

Начиная с 8 класса, умение решать квадратные уравнения является основополагающим, так как они находят широкое применение в решении тригонометрических, логарифмических, иррациональных, показательных и других видов уравнений. Квадратное уравнение широко распространено: во многих строительных и архитектурных расчётах, сооружениях, спорте, описании траектории движения планет. Поэтому исследование способов решения полных квадратных уравнений считаю актуальным.

Проблема: какие существуют способы решения полных квадратных уравнений?

Цель работы: изучить и систематизировать способы решения полных квадратных уравнений.

Изучить литературу по теме исследования.

Выбрать и изучить способы решения полных квадратных уравнений.

Объект исследования: полные квадратные уравнения.

Методы исследования: теоретический (изучение литературы), математический (построение графиков, вычисления).

Рассмотрим основные способы решения таких уравнений в нашей работе.

2.1 Квадратное уравнение: определение, виды, способы решения

Квадратным уравнением называется уравнение вида ax ² + bx + c =0, где х-переменная, a , b и c – некоторые числа, причём а¹0. Коэффициенты имеют свои названия: а – первый или старший коэффициент, в – второй коэффициент, с – свободный член. Если а=1, то уравнение называется приведённым. Если в=0 или с=0, то квадратное уравнение называют неполным (рис.1).

Рис.1 Виды квадратных уравнений

Примеры полных квадратных уравнений: 3x 2 -5x+2=0, x 2 -16x+24=0;

неполные: x 2 + 3x=0, 2x 2 — 128=0, 62x 2 = 0.

Корнями квадратного уравнения называются значения переменной, при которых уравнение обращается в верное равенство. Квадратное уравнение может иметь два, один или ни одного корня. [1]

В школьном курсе математики изучается несколько способов решения полных квадратных уравнений. Однако имеются и другие способы, которые позволяют очень быстро и рационально решать многие уравнения, всего насчитывается более десятка способов. Рассмотрим основные: решение квадратных уравнений по формуле, решение уравнения выделением полного квадрата, решение уравнения путём разложения левой части на множители, решение с помощью теоремы Виета и графический способ. Но сначала обратимся к историческим сведениям: как давно возникли квадратные уравнения и как их решали раньше?

2.2 Из истории квадратных уравнений

Квадратные уравнения в Индии.

Задачи на квадратные уравнения встречаются уже в астрономическом тракте «Ариабхаттиам», составленном в 499г. индийским математиком и астрономом Ариабахаттой. Другой индийский ученый, Брахмагупта ( VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:

ах 2 + b х = с, а > 0

В уравнении все коэффициенты, кроме а, могут быть отрицательными. Правило Брахмагупта (приложение 1) по существу совпадает с ныне существующими.

Квадратные уравнения в Древнем Вавилоне

Квадратные уравнения умели решать около 2000 лет до н.э. вавилоняне. Если применить современную алгебраическую запись, то в их клинописных текстах можно встретить неполные и полные квадратные уравнения, например:

х 2 + х = , х 2 – х = 14

Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. [5]

Квадратные уравнения в Европе XIII — XVII вв.

Формулы решения квадратных уравнений по образцу аль-Хорезми (приложение 1) в Европе были впервые изложены в «Книге абака», написанной в 1202г. итальянским математиком Леонардо Фибоначчи. Этот объемный труд, в котором отражено влияние математики как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошёл к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из «Книги абака» переходили почти во все европейские учебники XVI — XVII вв. и частично XVIII век.

Общее правило решения квадратных уравнений, приведённых к единому каноническому виду

при всевозможных комбинациях знаков коэффициентов b и с было сформулировано в Европе лишь в 1544г. М.Штифелем.

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, кроме положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других учёных способ решения квадратных уравнений принимает современный вид. [3]

2.3 Решение квадратных уравнений по формуле

Решение квадратных уравнений сводится к нахождению дискриминанта, чтобы определить количество корней: D=b 2 — 4aс.

Если D>0, то уравнение имеет два корня и находим эти корни по формуле:

Если D=0, то уравнение имеет один корень

Рассмотрим пример 1: нужно найти корни уравнения 3x 2 — 2x — 16=0.

Записываем сначала, чему равны числовые коэффициенты a, b и c:

a=3,b= -2,c= -16. Находим дискриминант: D=b 2 -4ac = (-2) 2 -4∙2∙(-16)=4+192=196

Дискриминант больше нуля, следовательно, у нас два корня, найдем их:

Х₁= (2 – 14) /6 = -2 Х₂ = (2 + 14) /6 = 8/3

Рассмотрим пример 2: найти корни уравнения x 2 — 6x + 11=0.

a=1,b= -6,c= 11. Находим дискриминант: D=b 2 -4ac = (-6) 2 -4∙1∙11= 36 — 44= — 8

Дискриминант меньше нуля, следовательно, корней нет.

Ответ: корней нет.

Рассмотрим пример 3: найти корни уравнения 4x 2 — 12x + 9=0.

a=4,b= -12,c= 9. Находим дискриминант: D=b 2 -4ac = (-12) 2 -4∙4∙9= 144 -144= 0

Дискриминант равен нулю, следовательно, у нас один корень:

2.4 Решение квадратных уравнений методом выделения полного квадрата

Поясним этот метод на примере 4: решим уравнение х 2 + 6х – 7 = 0.

Выделим в левой части полный квадрат. Для этого запишем выражение

х 2 + 6х в виде: х 2 + 6х = х 2 + 2· х ·3.

В полученном выражении первое слагаемое – квадрат числа х, а второе – удвоенное произведение х на 3, поэтому, чтобы получить полный квадрат, нужно прибавить 3 2 , так как х 2 + 2· х ·3 + 3 2 = (х + 3) 2 .

Преобразуем теперь левую часть уравнения х 2 + 6х – 7 = 0, прибавляя к ней и вычитая 3 2 . Имеем:

х 2 + 6х – 7 = х 2 + 2· х ·3 + 3 2 – 3 2 – 7 = (х + 3) 2 – 9 – 7 = (х + 3) 2 – 16.

Таким образом, данное уравнение можно записать так:

(х + 3) 2 –16 = 0, т.е. (х + 3) 2 = 16.

Следовательно, х + 3 = 4, х₁ = 1, или х + 3 = — 4 , х₂ = – 7.

2.5 Разложение левой части квадратного уравнения на множители

Рассмотрим пример 5: решим уравнение х 2 + 10х – 24 = 0.

Разложим левую часть уравнения на множители:

х 2 + 10х – 24 = х 2 + 12х – 2х – 24 = х(х + 12) – 2(х +12) = (х + 12)(х – 2).

Следовательно, уравнение можно переписать так:

Так как произведение равно нулю, то, по крайне мере один из его множителей равен нулю. Поэтому левая часть уравнения обращается в нуль при х = 2, а также при х = — 12. Это означает, что числа 2 и – 12 являются корнями уравнения х 2 + 10х – 24 = 0.

2.6 Графический способ решения

Если в уравнении x 2 + bx + c = 0

перенести второй и третий члены в правую часть, то получим x 2 = – bx – c .

Построим графики зависимостей у = х 2 и у = – bx – c .

График первой зависимости – парабола, проходящая через начало координат.

График второй зависимости – прямая. Возможны следующие случаи:

прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;

прямая и парабола могут касаться (только одна общая точка), т.е. уравнение имеет одно решение;

прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней. [2]

Пример 6: решим графически уравнение х 2 –3х – 4 = 0.

Запишем уравнение в виде х 2 = 3х + 4. Построим параболу у = х 2 и прямую у = 3х + 4. Прямую у = 3х + 4 можно построить по двум точкам М(0;4) и N (3;13).

Прямая и парабола пересекаются в двух точках А и B с абсциссами х₁ = – 1 и х₂ = 4. (Рис.2)

2.7 Решение квадратных уравнений с помощью теоремы Виета

1. Приведенное квадратное уравнение имеет вид х 2 + px + q = 0.

Его корни удовлетворяют теореме Виета, которая при а = 1 имеет вид

Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).

Если свободный член q приведенного уравнения положителен ( q >0), то уравнение имеет два одинаковых по знаку корня и это зависит от второго коэффициента p .

Если p >0, то оба корня отрицательные, если p 2 – 3х + 2 = 0; х₁ = 2 и х₂ = 1, так как q = 2 > 0 и p = – 3 2 +8х + 7 = 0; х₁ = – 7 и х₂ = – 1, так как q = 7 > 0 и p = 8 >0.

Если свободный член q приведенного уравнения отрицателен ( q p p >0.

х 2 + 4х – 5 = 0; х₁ = – 5 и х₂ = 1, так как q = – 5 p = 4 > 0;

х 2 – 8х – 9 = 0; х₁ = 9 и х₂ = – 1, так как q = – 9 p = – 8 >0.

2. Теорема Виета для квадратного уравнения ах 2 + b х +с = 0 имеет вид

Справедлива теорема, обратная теореме Виета:

Если числа х₁ и х₂ таковы, что х₁+х₂ = — b , х₁х₂ = c , то х₁ и х₂ – корни квадратного уравнения х 2 + b х + c = 0.

Эта теорема позволяет в ряде случаев находить корни квадратного уравнения без использования формулы корней. [4]

Пример 7: решим уравнение х 2 – 9х + 14 =0.

Найдём два числа х₁ и х₂ , такие, что

Такими числами являются 2 и 7. По теореме, обратной теореме Виета, они и служат корнями заданного квадратного уравнения.

При решении квадратного уравнения не надо ограничиваться одним

способом решения уравнения, который изучается в школьном курсе математики, а для каждой ситуации можно использовать свой способ решения.

Особенно популярным способом является решение квадратного уравнения по формуле и теорема Виета. Изучив материалы для подготовки к ГИА, я пришла к выводу: материалы содержат много квадратных уравнений, при решении которых можно использовать различные способы.

Интересным для меня оказался графический способ решения квадратного уравнения. Но недостаток этого способа – не всегда значения абсцисс точек пересечения графиков будут являться целыми и точными значениями.

Более подробно изучив тему «Решение полных квадратных уравнений», я углубила знания в истории развития математики и открыла много полезного и нового для себя. Кроме вышеперечисленных мною основных способов решения квадратных уравнений в разных источниках выделяют ещё: решение уравнений способом «переброски», решение с помощью циркуля и линейки, решение с помощью номограммы, геометрический способ и использование свойств коэффициентов квадратного уравнения.

Такая широкая тема позволяет всем желающим находить в книгах, научных журналах, сайтах всё новые пути решения уравнений, создавать основу для дальнейших исследований в мире математики, получать необходимые интересующие сведения, применение которых на практике способствует развитию мышления и повышению уровня знаний. Каждый из способов удобен по-своему, интересен и значим в общей копилке умений каждого.

Список использованных источников и литературы

Мерзляк А.Г. Алгебра: 8 класс: учебник для общеобразовательных организаций/А.Г.Мерзляк, В.Б.Полонский, М.С.Якир. – М.:Вентана – Граф, 2017.

Окунев А.К. Квадратичные функции, уравнения и неравенства / Пособие для учителя. — М.: Просвещение, 2016.

Соломник В.С., Милов П.И. Сборник вопросов и задач по математике. Изд. — 4-е, дополн. — М.: Высшая школа, 2017.

Якушева Г.Н. Математика. Справочник школьника. — М., Просвещение, 2015.

История возникновения квадратных уравнений: [Электронный ресурс]. URL : https://ru.wikipedia.org/wiki/Квадратное_уравнение (Дата обращения 26.03.2019).

Индийский математик Брахмагупта и среднеазиатский учёный, математик, астроном Абу́ Абдулла́х Муха́ммад ибн Муса́ аль-Хорезми́

Видео:Быстрый способ решения квадратного уравненияСкачать

Исследовательская работа «Способы решения квадратных уравнений»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Очень полезно решать одну и ту же задачу различными способами. Так мы нарабатываем опыт, умение сравнивать и выбирать рациональные решения, подойти к решению с разных сторон. Квадратные уравнения нам приходится решать очень часто. И это одна из основных тем ОГЭ. В школьной программе нам дают только несколько способов. Стало интересно, какие еще способы есть, какой из способов самый легкий и рациональный. Чем можно заинтересовать одноклассников? Какие способы появились первыми? Изучить и обобщить материал.

Гипотеза : Я предположил, что есть способы рациональнее, чем нам дают в школьном курсе. Мне хочется узнать, какие еще есть способы решения и нужно ли их включить в программу школьного курса .

Цель исследования: Изучить различные способы решения квадратных уравнений и научиться их применять на практике. Сколькими способами можно решить одно квадратное уравнение. Изучить и познакомить одноклассников.

собрать информацию о различных способах решения квадратных уравнений;

разобрать на примерах;

вывести плюсы и минусы данного способа;

познакомить одноклассников с большим выбором способов.

Объект исследования: квадратные уравнения.

Предмет исследования: способы решения квадратных уравнений.

Методы исследования: сбор и изучение информации, анализ, сравнение и проверка на практике разных способов.

Научиться решать одно и то же квадратное уравнение разными способами.

Определение квадратного уравнения и его виды

Квадратным уравнением называется уравнение вида ax 2 + bx + c = 0,

где х — переменная , а, b и с -некоторые числа, причем, а ≠ 0.

а – первый или старший коэффициент при ; b – второй или коэффициент при х; с – свободный член от переменной х .

Если старший коэффициент равен 1 , то квадратное уравнение приведенным .

Полное квадратное уравнение – это уравнение, у которого коэффициенты b и с отличны от нуля.

Неполное квадратное уравнение – это уравнение, у которого хотя бы один из коэффициентов b или с равен нулю.

Коэффициент а всегда присутствует в квадратном уравнении, а ≠ 0.

Корнем квадратного уравненияax 2 + bx + c = 0, называют всякое значение переменной х , при котором квадратный трехчлен ax 2 + bx + c обращается в нуль.

Решить квадратное уравнение – это значит найти все его корни или установить, что их нет.

Я рассмотрел много уравнений. В данной работе представлю приведенное уравнение решенное разными способами.

Способы решения квадратных уравнений

1способ: Решение квадратных уравнений по формуле.

Уравнение вида: ax 2 + bx + c = 0, можно решить по формулам. Число действительных корней уравнения зависит от знака дискриминанта D = b 2 − 4ac

2способ: Решение квадратного уравнения графическим способом.

1)Перенести в уравнении aх 2 + bx + c = 0 второй и третий члены в правую часть, получим aх 2 = — bx — c .

2)Разделим обе части уравнения на коэффициент а ≠ 0.

3)Получаем уравнение: х 2 = — px – q, где p=b/a и q=c/a .

4)Построим в одной системе координат графики зависимости:

График первой зависимости – парабола, проходящая через начало координат. График второй зависимости – прямая.

Возможны следующие случаи:

прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;

прямая и парабола могут касаться (только одна общая точка), т.е. уравнение имеет одно решение;

прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.

3 способ : Решение квадратных уравнений, используя теорему Виета .

4 способ : Решение квадратных уравнений, используя свойства коэффициентов.

Пусть дано квадратное уравнение ax 2 + bx + c = 0, , где а ≠ 0.

1 0 Если а + b + с = 0 ( т.е. сумма коэффициентов равна нулю), то х ₁ = 1, х ₂ = с/а.

2 0 Если а + с = b ( т.е. сумма крайних коэффициентов равна среднему коэффициенту), то х ₁ = -1, х ₂ = — с/а.

3 0 Если дано уравнение вида: ax 2 + (а 2 + 1)x + а = 0, то х ₁ = -а, х ₂ = — 1/а.

5 способ: Решение квадратных уравнений с помощью разложения левой части уравнения на множители способом группировки.

6 способ : Решение квадратных уравнений методом выделения полного квадрата .

Применяя формулы сокращенного умножения

7способ: Решение квадратных уравнений геометрическим способом

Площади

1) Квадрат со стороной х

2) 2х четыре прямоугольника (х*0,5)

3) достроили до большого квадрата со стороной (1+х) т.е. 0,5+х+0,5

Общая площадь равна +4*0,25=

8 способ : Решение квадратных уравнений с помощью циркуля и линейки .

Построим точки S( (центр окружности) и A(0; 1) .

Проведем окружность с радиусом SA ;

Абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.

9 способ : Решение квадратных уравнений с помощью номограммы .

Номограмма для решения уравнения z 2 + pz + q = 0.

Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.

10 способ : Решение квадратных уравнений, используя теорему Безу.

Теорема Безу: Остаток при делении многочлена P( x ) на многочлен х – а равен значению этого многочлена при х = а , то есть P (а).

Теорема Безу дает возможность, найдя один корень многочлена и искать далее корни многочлена, степень которого на 1 меньше: если Р(а) = 0 , то Р(х)= (x — а)Q(x), и остается решить уравнение Q(x) = 0 .

Делители с это 3 и -3

В ходе исследовательской работы была проведена работа среди моих одноклассников. В моем классе 22 человека, я познакомил их с презентацией по решению квадратных уравнений разными способами. Мне нужно было выяснить интерес к моей теме, понятность изложения способов и применение в дальнейшем. Большей части класса было сложно понять и закреплять способы на практике они не стали.

Пять одноклассников решились принять участие в тестирование, целью которой было привлечь к изучению математики и выявить, какой способ решения квадратного уравнения рациональнее. С помощью всех методов предложено было решить два уравнения (приведенное и не приведенное). Результаты проверки в таблице.

Решение квадратных уравнений по формуле. Можно применять ко всем квадратным уравнениям, только знать формулы.

Решение квадратного уравнения графическим способом. Наглядный способ, легко увидеть количество корней. Минус способа, когда корни дробные или слишком большие не показать точки пересечения из-за масштаба.

Решение квадратных уравнений, используя теорему Виета. Легко решаются только приведенные уравнения с целыми корнями. Хороший способ для проверки.

Решение квадратных уравнений, используя свойства коэффициентов. Не все уравнения решаются данным способом.

Решение квадратных уравнений с помощью разложения левой части уравнения на множители способом группировки. Необходимо правильно увидеть как разложить вх на два слагаемых. Развивает логику.

Решение квадратных уравнений методом выделения полного квадрата. Необходимо помнить формулы сокращенного умножения. Способ поможет при построение графика квадратичной функции.

Решение квадратных уравнений геометрическим способом. Хороший способ, с помощью площадей. Находим положительные корни.

Решение квадратных уравнений с помощью циркуля и линейки. Знание формулы нахождения центра. Иметь циркуль. Наглядный способ если корни целые, могут быть неточности.

Решение квадратных уравнений с помощью номограммы. Нужно иметь при себе номограмму. Мы находили только положительные корни.

Решение квадратных уравнений, используя теорему Безу. Хороший способ на будущее при решение уравнений высших степеней. Трудоемкий. Хороший способ для целых корней.

В ходе выполнения данной исследовательской работы мне удалось обобщить изученный материал, провести урок для своих одноклассников. Найти новые способы для себя. Для меня эта работа открыла возможности применять полученные знания и делится со своими сверстниками. Моих одноклассников, пусть и не многих, заинтересовали эти способы. Мне стало понятно почему в школьной программе дают основные способы. Я получил и хорошую практику в наборе математических формул и практику работы в программе Excel по созданию формул. Мне понравился способ выделение полного квадрата и способ используя теорему Безу, эти знания я буду применять не только для решения квадратных уравнений.

Алгебра: 8 класс: учебник для общеобразовательных организаций/ Мерзляк А.Г., Полонский В.Б., Якир М.С., издательский центр «Вентана_Граф», 2015

Алгебра: 9 класс: учебник для общеобразовательных организаций/ Мерзляк А.Г., Полонский В.Б., Якир М.С., издательский центр «Вентана_Граф», 2014

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

12 способов решения квадратных уравнений

В работе рассматриваются способы решения квадратных уравнений, которых нет в учебнике. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Однако, значение квадратных уравнений заключается не только в изяществе и краткости решения задач, хотя и это весьма существенно. Не менее важно и то, что в результате применения кваратных уравнений при решении задач обнаруживаются новые детали, удается сделать интересные обобщения и внести уточнения, которые подсказываются анализом полученных формул и соотношений.

Просмотр содержимого документа
«12 способов решения квадратных уравнений »

1.Определение квадратного уравнения, его виды 4

2. Способы решения квадратных уравнений 4

2.1 Решение неполных квадратных уравнений. 4

2.2 Разложение левой части уравнения на множители. 1. СПОСОБ 5

2.3 Метод выделения полного квадрата. 2. СПОСОБ 5

2.4 Решение квадратных уравнений по формуле. 3. СПОСОБ 5

3.5 Решение уравнений с использованием теоремы Виета. 4. СПОСОБ 6

3.6 Решение уравнений с использованием теоремы Виета 5. СПОСОБ 6

3.7 Решение уравнений способом «переброски». 6. СПОСОБ 6

3.8 Свойства коэффициентов квадратного уравнения. 7. СПОСОБ 7

3.9 Графическое решение квадратного уравнения. 8. СПОСОБ 8

3.10 Решение квадратных уравнений с помощью

циркуля и линейки. 9. СПОСОБ 8

3.11 Решение квадратных уравнений с помощью номограммы. 10. СПОСОБ 9

3.12 Геометрический способ решения квадратных уравнений. 11. СПОСОБ 10

3.13 Способ решения квадратных уравнений по теореме Безу. 12. СПОСОБ 10

Список литературы 12

Приложение 2 ЗАДАЧИ

Приложение 3 Из истории квадратных уравнений

Уравнения второй степени умели решать еще в древнем Вавилоне. Математики Древней Греции решали квадратные уравнения геометрически; например, Евклид — при помощи деления отрезка в среднем и крайнем отношениях. Задачи, приводящие к квадратным уравнениям, рассматриваются во многих древних математических рукописях и трактах.

Вывод формулы решения квадратного уравнения в общем, виде имеется у Виета. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.

Впервые квадратное уравнение сумели решить математики Древнего Египта.
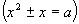
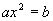
Неполные квадратные уравнения и частные виды полных квадратных уравнений умели решать вавилоняне (около 2 тыс. лет до н. э.). Об этом свидетельствует найденные клинописные тексты задач с решениями (в виде рецептов). Некоторые виды квадратных уравнений, сводя их решение к геометрическим построениям, могли решать древнегреческие математики. Приемы решения уравнений без обращения к геометрии дает Диофант Александрийский (III в.). В дошедших до нас шести из 13 книг «Арифметика» содержатся задачи с решениями, в которых Диофант объясняет, как надо выбрать неизвестное, чтобы получит решение уравнения вида . Способ решение полных квадратных уравнений Диофант изложил в книгах «Арифметика», которые не сохранились.

Формулы решения квадратных уравнений в Европе были впервые изложены в 1202 г. итальянским математиком Леонардом Фибоначчи.

Общее правило решения квадратных уравнений, приведенных к виду 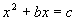, было сформулировано немецким математиком М. Штифелем (1487 — 1567). Выводом формулы решения квадратных уравнений общего вида занимался Виет. После трудов нидерландского математика А. Жирара (1595 — 1632), а также Декарта и Ньютона способ решения квадратных уравнений принял современный вид.
Формулы, выражающие зависимость корней уравнения от его коэффициентов, были выделены Виетом в 1591 г.

И сейчас квадратные уравнения очень актуальны. Одна из основных тем ОГЭ – это квадратные уравнения.

Одной из основных тем, проверяемых на экзамене по математике, является тема «Квадратные уравнения». Данная тема изучается в 8 классе, а на повторение данной темы в 9 классе отводится один час. Я надеюсь , что эта работа поможет сдать экзамен по алгебре на более высокий бал.

Также квадратные уравнения используются в физике и в химии для решения задач в 10 и 11 класса, знание данной темы поможет при сдаче ЕГЭ по этим предметам.

Научиться решать квадратные уравнения различными способами.

Для достижения цели мы поставили перед собой следующие задачи

1.Изучить литературу по выбранной теме;

2.Изучить историю возникновения и решения квадратных уравнений;

3.Изучить способы решения квадратных уравнений разного вида;

4. Подобрать дидактический материал по теме работы

Объект исследования – квадратные уравнения.

При выполнении исследования применялись такие методы, как сравнительный анализ литературы, сбор и обработка фактов с помощью анализа, сравнения и аналогии.

1.Определение квадратного уравнения, его виды.

Определение: Квадратным уравнением называется уравнение вида

где х— переменная, а,b и с-некоторые числа, причем, а ≠ 0.

Коэффициенты а, b, с, различают по названиям: а – первый или старший коэффициент; b – второй или коэффициент при х; с – свободный член, свободен от переменной х.

Квадратное уравнение также называют уравнением второй степени, так как его левая часть есть многочлен второй степени

Квадратное уравнение называют приведенным, если старший коэффициент равен 1; квадратное уравнение называют неприведенным, если старший коэффициент отличен от 1.

х²+рх+q=0 – стандартный вид приведенного квадратного уравнения

кроме приведенных и неприведенных квадратных уравнений различают также полные и неполные уравнения.

Полное квадратное уравнение – это квадратное уравнение, в котором присутствуют все три слагаемых; иными словами, это уравнение, у которого коэффициенты b и с отличны от нуля.

Неполное квадратное уравнение – это уравнение, в котором присутствуют не все три слагаемых; иными словами, это уравнение, у которого хотя бы один из коэффициентов b и с равен нулю.

Обратите внимание: об ах² речи нет, этот член всегда присутствует в квадратном уравнении.

1) ах 2 + с = 0, где с ≠ 0;

2) ах 2 + bх = 0, где b ≠ 0;

Корнем квадратного уравнения ах²+вх+с=0 называют всякое значение переменной х, при котором квадратный трехчлен ах²+bх+с обращается в нуль; такое значение переменной х называют также корнем квадратного трехчлена.

Можно сказать и так: корень квадратного уравнения ах²+bх+с=0 – это такое значение х, подстановка которого в уравнение обращает уравнение в верное числовое равенство. 0=0.

Решить квадратное уравнение – это значит найти все его корни или установить, что их нет.

2.Способы решения квадратных уравнений

2.1 Решение неполных квадратных уравнений.

Сначала математики научились решать неполные квадратные уравнения, поскольку для этого не пришлось, как говорится, ничего изобретать.

🌟 Видео

Метод выделения полного квадрата. 8 класс.Скачать

Квадратное уравнение. 1 урок.Скачать

Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать

Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Неполные квадратные уравнения. Алгебра, 8 классСкачать

Формула корней квадратного уравнения. Алгебра, 8 классСкачать

ТЕОРЕМА ВИЕТА ЗА 2 МИНУТЫСкачать

Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Теорема Виета. 8 класс.Скачать

Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Как решать квадратные уравнения без дискриминантаСкачать

САМЫЙ ЛЕГКИЙ способ решения Квадратного Уравнения #shorts #youtubeshortsСкачать

Многие не знают этот способ решения квадратного уравнения!Скачать

ПРОСТЕЙШИЙ способ решения Квадратного Уравнения #shorts #youtubeshortsСкачать

Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать

РЕШЕНИЕ НЕПОЛНОГО КВАДРАТНОГО УРАВНЕНИЯ ЗА 5 СЕКУНДСкачать

5 способов решения уравнений | Эрик Легион | 100балльный репетиторСкачать