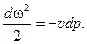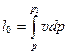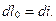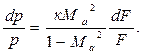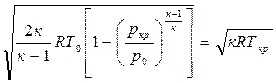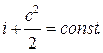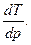Если движение газа через канал установившееся, то через каждое сечение канала в единицу времени протекает одно и то же количество газа.
Для этого случая (рис. 12.1) при определенной скорости газа в каждом сечении канала расход газа будет равен

где G — секундный массовый расход газа;
w1,w2,w3— расходные скорости в соответствующих поперечных сечениях;
v1, v2, v3 — удельные объемы в отдельных поперечных сечениях.
Постоянство массового расхода для всех сечений канала в каждый момент времени устанавливает условие неразрывности струи, поэтому уравнение (12.1) называют уравнением неразрывности или сплошности.
Для рассматриваемого процесса течения газа через канал уравнение первого закона термодинамики для G кг газа имеет вид

где 



 |
| Рис. 12. 1 |
Работа газа против внешних сил в движущемся газе является работой, затраченной на его проталкивание.
Рассмотрим поток газа в канале
(рис. 12.1) при одномерном течении. Выделим сечениями I—I и II—II некоторую массу газа. Притекающий к сечению I—I поток выполняет функцию поршня, который вытесняет заполняющий канал газ. На выделенную массу газа в канале будет действовать слева сила pF, а справа — сила (р+dp) (F + dF).
Работа перемещения, учитывая принятые в термодинамике знаки работ, будет равна

После сокращения и отбрасывания малых величин второго и высшего порядка получим
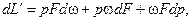

Так как по уравнению неразрывности Fw = Gv и, учитывая то, что расход G есть величина постоянная, в сплошной среде


Относя работу против внешних сил к 1 кг газа, получим
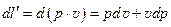
Величина 
Второе слагаемое 
Подставляя работу против внешних сил в уравнение первого закона термодинамики, записанное для 1 кг газа, будем иметь

Как известно из уравнения (3.10),


Это уравнение показывает, что теплота, сообщаемая движущемуся газу, расходуется в двух направлениях: на приращение энтальпии газа и на приращение внешней кинетической энергии, т. е. идет на увеличение скорости газового потока.
Уравнение (12.11) является основным для потока газа или пара, причем оно справедливо как для обратимых, не сопровождающихся действием сил трения, так и для необратимых течений, сопровождающихся трением.
Для течений при наличии сил трения уравнение (12.11) должно быть дополнено 2-мя членами: один, учитывающий работу, расходуемую на преодоление сил трения, другой, выражающий приращение тепла в газовом потоке. Так как работа против сил трения полностью переходит в тепло, то эти два члена одинаковы по величине, имеют различный знак и поэтому взаимно уничтожаются. Наличие сил трения не может нарушить общего баланса Энергии, а лишь приводит к преобразованию одного вида энергии в другой.
При адиабатном течении газа, когда при движении газа через канал тепло ему не сообщается (dq = 0), будем иметь

Из уравнения (12.12) следует, что при теплоизолированном стационарном течении газа через канал сумма удельной энтальпии и удельной кинетической энергии сохраняет постоянное значение.
Уравнение (12.12) так же, как и (12.11), сохраняет силу как для обратимых, так и для необратимых течений. Следует отметить, что эти уравнения справедливы лишь в том случае, когда газ или жидкость при своем движении совершает работу расширения и не производит полезной (технической) работы (например, вращение рабочего колеса какой-либо машины, приводимой в движение потоком газа).
Для обратимого процесса истечения газа одновременно с уравнением (12.11) сохраняет силу и уравнение (4.7):
Подставив последнее уравнение в формулу (12.11), получим
Приращение внешней кинетической энергии тела является как бы располагаемой работой, которая может быть использована в машинах и превращена в другие виды энергии.
Обозначим располагаемую работу через l0, тогда

Равенство (12.12) устанавливает основные особенности истечения газов. Из этого равенства видно, что w и dp имеют обратные знаки, т. е. при обратимом процессе увеличение скорости всегда связано с понижением давления, и наоборот, уменьшение скорости сопровождается повышением давления.
 |
| Рис. 12.2 |
Каналы. в которых происходит расширение газа с уменьшением давления (dp 0), называются соплами.
Каналы, в которых происходит сжатие газа с увеличением давления (dp > Q) и уменьшением скорости (dw 0. Если в течение процесса давление будет оставаться постоянным с/р = 0, то располагаемая работа будет равна нулю. Если процесс изменения состояния газа при его течении изобразить линией в координатах р—v (рис. 12.2), то для процесса истечения А — В располагаемая работа
изобразится в виде площади, ограниченной кривой процесса, изобарами р = р1 и p = p2 и осью ординат. Работа расширения газа
будет по-прежнему изображаться площадью под кривой процесса, которая ограничена крайними ординатами и осью абсцисс.
В зависимости от вида процесса значение располагаемой работы может быть подсчитано на основе общих термодинамических положений. Располагаемая работа в политропном процессе, в котором изменение состояния подчиняется уравнению (pv n = const), после подстановки в уравнение (12.13) значения текущего объема

В общем случае располагаемая работа может быть больше или меньше работы расширения или равна ей, причем это соотношение будет определяться величиной показателя политропы. Так, для политропного процесса, в котором работа расширения газа определяется по формуле
сравнение с располагаемой работой приводит к равенству
Для адиабатного процесса расширения газа
Для адиабатного течения газа располагаемая работа может быть определена и через энтальпию газа. Используя уравнение (12.12), видим, что
Интегрируя это выражение, получим

Следовательно, располагаемая работа газа при адиабатном течении будет равна разности энтальпий в начальном и конечном состояниях. Эта разность энтальпий обозначается через h0 и носит название располагаемого теплоперепада.
На рис. 12.3 и 12.4 показаны располагаемый теплоперепад и располагаемая работа в диаграмме i — s.
Видео:Все формулы молекулярной физики, МКТ 10 класс, + преобразования и шпаргалкиСкачать

ТЕРМОДИНАМИКА ГАЗОВОГО ПОТОКА
4.1. Уравнения и параметры движущегося газа
В рассмотренных выше процессах не учитывалась кинетическая энергия рабочего тела. Однако в теплотехнике широко распространены энергетические установки, в которых преобразование энергии осуществляется в движущемся газе. Такие процессы происходят в турбинах, реактивных двигателях, лопаточных и струйных компрессорах и т.п.
Рассмотрим уравнения термодинамики для стационарного одномерного потока идеального газа.
Для газового потока в любом сечении справедливо уравнение состояния, записанное через плотность:
где p – давление в рассматриваемом сечении;
ρ – плотность газа в этом сечении;
R – газовая постоянная;
T – термодинамическая температура (температура, которую покажет в данном сечении безинерционный термометр, перемещающийся со скоро-стью газового потока).
В термодинамике величину скорости потока газа обозначают с и измеряют в м/с. Часто с целью количественной оценки величины скорости потока ее сравнивают со скоростью распространения слабых возмущений в среде газа. При выведении газа из равновесия в каком-либо месте в нем возникает движение частиц. Эти возмущения передаются по всему газу (подвижному и неподвижному) с так называемой с к о р о с т ь ю з в у к а. Скорость звука обозначается a, измеряется в м/с и вычисляется поизвестной из физики формуле:
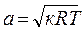
Если c 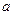
4.1.1. Уравнение энергии
В движущемся газе выделим сечениями 1-1 и 2-2, Рис. 4.1, участок потока.
На основании первого закона термодинамики для энергоизолирован- ного потока (данная система не обменивается теплотой и работой с окружающей средой) можем записать Е1 = Е2. Отсюда для m = 1кг газа уравнение (1.7) в сечениях потока будет иметь вид:
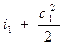
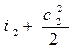
Это означает, что для любого сечения потока газа сумма энтальпии и кинетической энергии одинакова, т.е.
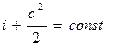
Выражение (4.3) называют у р а в н е н и е м э н е р г и и потока газа. Из него следует, что изменить скорость газа в потоке можно лишь только за счет изменения энтальпии.
Уравнение энергии можно записать в другом виде. Продифференцируем выражение (4.3) и получим: cdc = — di. Из первого закона термодинамики, записанного в виде dq = di -vdp, при dq = 0 следует, что di = vdp. Тогда
Выражение (4.4) приписывают Д. Бернулли, поэтому в технической литературе его называют у р а в н е н и е м Б е р н у л л и.
Это уравнение устанавливает связь скорости с давлением. Из него следует, что для увеличения скорости (dc > 0) необходимо снижение давления (dp
В окончательном виде формула температуры торможения имеет вид:
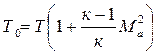
Используя адиабатную связь между температурой и давлением, получим формулу для давления торможения:
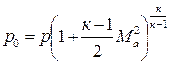
Плотность ρ0 определяется по p0 и T0 из уравнения (4.1).
4.1.3. Уравнение скорости движения газа
Уравнение скорости движения газа в произвольном сечении потока получим из уравнения энергии. Пусть газ вытекает из емкости, где его скорость была равна нулю. Тогда уравнение энергии для произвольного сечения потока газа и для сечения, где c = 0, будет иметь вид:
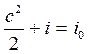
c = 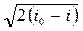
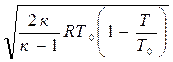
Если отношение температур заменить отношением давлений, то
c= 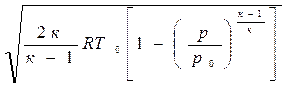
Из выражения (4.7) следует, что величина скорости газа в рассматриваемом сечении потока зависит от природы газа, от параметров в его исходном (заторможенном) состоянии и от давления газа в рассматриваемом сечении.
4.1.4. Уравнение расхода
Термодинамика газового потока в основном рассматривает стационарное движение газа. Это означает, что через все сечения канала в любой момент времени протекает одно и то же массовое количество газа. Обозначается секундный массовый расход 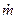
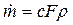
Выразим секундный массовый расход через параметры заторможенного газового потока, для чего в выражение (4.8) вместо c подставим его значение (4.7), а плотность представим в виде
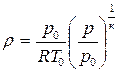
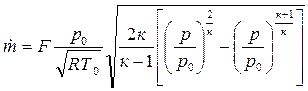
4.2. Течение газа в каналах
4.2.1. Уравнение обращения воздействия
Каналы, в которых газовый поток увеличивает свою скорость, называются с о п л а м и. Каналы, скорость в которых уменьшается, именуют д и ф -ф у з о р а м и. Геометрическая форма сопел может быть различной. Это зависит от того, каково внешнее воздействие на газовый поток.
В 1948 г. А.А. Вулис получил зависимость, выражающую связь геометрии сопла с характером внешнего воздействия на поток. Для неэнергоизолированного движения газа зависимость Вулиса имеет вид:
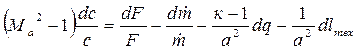
Здесь первое слагаемое правой части уравнения выражает г е о м е т-
р и ч е с к о е в о з д е й с т в и е на движущийся газ, второе – м а с с о в о е, третье – т е п л о в о е и четвертое – м е х а н и ч е с к о е. Уравнение (4.10) является математическим выражением принципа обращения воздействия, суть которого состоит в том, что характер влияния каждого воздействия на газовый поток противоположен при сверхзвуковых и дозвуковых течениях газа.
Проанализируем лишь геометрическое воздействие. В этом случае из уравнения (4.10) следует:
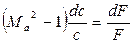
При дозвуковом течении газа (Мa 0, а в расширяющемся, где dF > 0, – тормозиться, т.е. dc 1) знаки у величин dc/c и dF/F одинаковые. Следовательно, для увеличения скорости необходим расширяющий канал, а для торможения — сужающийся.

4.2.2 Течение газа в соплах Лаваля
При движении газа вдоль сверхзвукового геометрического сопла своеобразно изменяются его параметры. Для выявления характера изменения давления по длине сопла из уравнений (4.4) и (4.11) можно получит выражение:
Из анализа данного уравнения следует, что давление вдоль сопла уменьшается. Кривая давления в дозвуковой части сопла имеет выпуклый вид, а в сверхзвуковой – вогнутый. Температура вдоль сопла уменьшается, так как процесс расширения газа адиабатный. С такой же закономерностью уменьшается по длине сопла и скорость звука.
Характер изменения скорости вдоль сопла устанавливается уравнением Бернулли (4.4), записанным в виде:
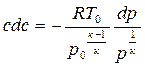
В сужающейся части сопла это вогнутая кривая. а в расширяющейся – выпуклая, асимптотически приближающаяся к максимально возможной скорости при р = 0. Качественные изменения давления, температуры, скорости звука и скорости потока по длине геометрического сопла представлены на рис.4.3 .Характерным для канала такой формы является участок перехода дозвукового течения в сверхзвуковой.
Сечение канала, в котором скорость потока достигает величины, равной местной скорости звука, называют к р и т и ч е с к и м .

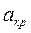
Получим выражение для ркр и Ткр через параметры торможения. В критическом сечении 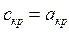
После незначительных преобра –
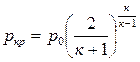
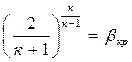
Величина β определяется только
значением показателя адиабаты к . Рис. 4.3
Так, для воздуха при к = 1,4 значение βкр = 0,528. Отсюда следует, что для воздуха критическое давление меньше давления торможения в 1,89 раза.
Значение критической температуры получим из выражения (4.12), заменив отношение давлений отношением температур:
Ткр= Т0 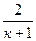
Теперь выражение для критической скорости можно представить в другом виде:
скр = 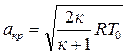
Скорость газа в каждом сечении сопла и на выходе из него вычисляется по формуле (4.7).
Если секундный массовый расход выразить через параметры торможения и площадь критического сечения, то зависимость (4.9) существенно упрощается:
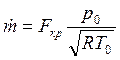
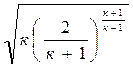
Если давление газа в выходном сечении сопла равно давлению окружающей среды ( 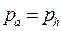
4.2.3. Дросселирование газа и пара
Д р о с с е л и р о в а н и е м называют процесс понижения давления в газовом потоке при преодолении местного сопротивления в канале.
При дросселировании газа или пара протекает необратимый процесс снижения давления без совершения внешней работы. Если в канале имеется местное сопротивление в виде резкого сужения вида перегородки с отверстием, задвижки, клапана и т.п., то газовый поток перестраивает свою геометрическую форму, как до сужения, так и после него. Перестройка формы потока и перетекание через само сужение связано с образованием вихревых движений газа. Часть кинетической энергии потока идет на образование вихрей, часть – на преодоление сопротивления трения. Затраченная на это энергия необратимо превращается в теплоту, которая воспринимается газом. Поэтому давление после местного сопротивления не восстанавливается до первоначального. Изменение давления, скорости и температуры по длине канала приведено на рис.4.4. Скорость газа при протекании его через сужение возрастает, что вызывает снижение давления и температуры. После сужения скорость понижается, но давление, вследствие указанных причин, не восстанавливается до первоначального.
Степень снижения давления газа при дросселировании зависит от природы газа и его состояния, относительной величины сужения, скорости газа. Обозначим степень снижения давления через 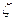

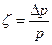
где ∆р – величина снижения давления;
р – давление на входе в сужение.
В энергетических установках дросселирование нежелательно, т.к. при падении давления снижаются энергетические возможности газа. Но иногда дросселирование является необходимым и создается искусственно, например, в редукторах, регуляторах и т.п.
При термодинамическом анализе особенностей процесса дросселирования целесообразно использовать общее уравнение энергии:
В канале можно обеспечить с1 = с2 , тогда i1 =i2. Из чего следует, что энта-
льпия газа в процессе дросселирования
остается постоянной. Рис. 4.4
Этот вывод справедлив как для идеальных, так и для реальных газов. При дросселирования идеального газа Т1 = Т2 , поскольку i1 = i2 . Это значит, что для идеального газа температура после дросселирования равна температуре на входе в дроссель.
Для реального газа изменение температуры при его дросселировании в отличие от идеального газа имеет своеобразный характер. Как показывают опыты, температура реального газа в результате дросселирования повышается, понижается или не изменяется. Это свойство впервые обнаружили ученые Д. Джоуль и У. Томсон, поэтому оно носит название э ф ф е к т а Д ж о у л я-Т о м с о н а.
Используя дифференциальные уравнения, связывающие i, s, ρ и T, можно получить для газа, подчиняющегося уравнению Ван-дер-Ваальса, следующую зависимость:
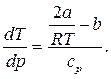
Отношение бесконечно малого изменения температуры к бесконечно малому изменению давления при дросселировании называется д р о с с е л ь—э ф ф е к т о м и обозначается
α =
Так как при дросселировании dp 0, т.е. dT 0 ( при T > 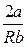
в) 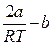
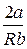
Изменение знака дроссель — эффекта α называется и н в е р с и е й,
а температура, при которой dT = 0, называется т е м п е р а т у о й и н в е р с и и и обозначается Tинв .
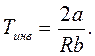
|
Понятие температуры инверсии особенно широко используется в холодильной и криогенной технике.
Каждый конкретный газ имеет индивидуальную температуру инверсии. Так, например, для воздуха Тинв = 650 К; для водорода Тинв = 204 К; для водяного пара Тинв= 682 К.
Для установления температуры реального газа после дросселя необходимо сравнить Tвх с Tинв .Если температура газа на входе в дроссель равна его температуре инверсии, то после дросселя она восстановится до прежнего значения. При Tвх Tинв — она возрастет. Характер изменения температуры при дросселировании

Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Основные уравнения газового потока(их 4 шт. полностью все с выводами )
Рассмотрим основные уравнения -рабочей среды применительно к одно мерному течению потока.
Уравнение состояния. Выражает зависимость между физическими пара метрами газа. Оно имеет вид:
где р — абсолютное давление, Па; u — удельный объем, м3/кг; R — газовая постоянная, Дж/(кг • К); Т — абсолютная температура, К.
Выразив удельный объем через плотность, уравнение состояния можно записать в другом виде:
де ρ = 1 u — плотность газа, кг/м3.
Уравнения (4.2) и (4.3) справедливы для идеальных газов, у которых газовая постоянная зависит только от природы газа. Несмотря на то что уравнения (4.2) и (4.3) выведены для идеального газа, они широко применяются в расчетах газовых турбин и компрессоров. Для воздуха газовая постоянная R = 287,1 Дж/(кг • К). Для газа — сме си продуктов сгорания с избыточным воздухом, являющейся рабочей средой в газовых турбинах, — она колеблется в пределах 277,6—284,5 Дж/(кг • К) в зависимости от коэффициента избытка воздуха. Уравнение (4.2) и (4.3) для расчета паровых турбин не применимы (особенно в случае влажного пара), так как газовая постоянная водяного пара существенно зависит от давления и температуры. На практике расчет пара метров паровых турбин ведется с помощью таблицы водяного пара и диаграммы i—s.
В некоторых случаях для определения удельного объема используется уравнение состояния перегретого пара, записанное в следущем виде:
где i — энтальпия перегретого пара, кДж/кг; ∆ — поправка на давление и энтальпию. (В пределах значений р и i, характерных для судовых паровых турбин, ∆составляет 0,455— 0,459).
К параметрам состояния относится удельная теплоемкость газа. Врас четах турбомашин (турбин и компрессоров) используется теплоемкость при постоянном давлении, отнесенная к 1 кг газа. Зависимость теплоемкости от температуры принимается линейной в виде ср = ар + bt, где ар и b — постоянные, зависящие от рода газа.
При р = const и t = 0° Степлоем кость воздуха ср = 1004 Дж/(кг • К). Теплоемкость газа при тех же условиях и сжигании топлива, используемого в судовых установках, находится в пределах 1007—1017 Дж/(кг • К). Меньшие значения соответствуют коэффициенту избытка воздуха α = 5,, большие — соответствуют α = 2,7.
В процессе расширения и сжатия температуры газа меняется, поэтому величина ср является переменной. Для упрощения расчетов теплоемкость чаще всего принимают постоянной и равной среднему ее значению в пределах температур начала t1 и конца t2 процесса. В этом случае теплоемкость рассчитывается по формуле
Значения постоянных ар, b, входящих в формулу (4.5), принимают: для воздуха ар = 1004, b= 0,186 • 10 -3 ; для газа ар = 1007 _1017,. b = 0,207 _ 0,262. Меньшие значения соответствуют коэффициенту избытка воздуха α = 5, большие — соответствуют α = 2,7.
В теории турбомашин используется следующая зависимость между показателемизоэнтропыk, теплоемкостью ср и газовой постоянной R:
Среднее значение показателя изоэнтропы расширения в судовых газовых турбинах k = 1,34 _ 1,35.
По формуле (4.6) находят газовую постоянную по принятым ср и k
🔥 Видео
Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Уравнение состояния идеального газа. Практическая часть. 10 класс.Скачать

Урок 195. Изотермы реального газаСкачать

Урок 157. Изопроцессы и их графики. Частные газовые законыСкачать

Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

10 класс | Газовые законы. ИзопроцессыСкачать
Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

Физика - Газовые законы. Уравнение идеального газа.Скачать

Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

Естествознание 10 класс (Урок№8 - Моделирование в науке.)Скачать

Урок 147. Задачи на основное уравнение МКТ идеального газаСкачать

Физика. Термодинамика: Внутренняя энергия идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Уравнение состояния идеального газаСкачать

Лекция №1 "Основные понятия молекулярной физики"Скачать

Термодинамические системы, параметры. Равновесное, неравновесное состояния терм. систем. 10 класс.Скачать

Применение первого закона термодинамики к изопроцессам. 10 класс.Скачать

Урок 194. Уравнение Ван-дер-ВаальсаСкачать