Какой геометрический объект на плоскости не может задать уравнение связывающее обе координаты

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Уравнения геометрических объектов на плоскости. Виды уравнений прямой на плоскости. Уравнение прямой проходящей через две точки

Страницы работы

Фрагмент текста работы

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Аналитическая геометрия изучает геометрические объекты и связи между ними используя их аналитические представления в виде уравнений.

Видео:ДЕКАРТОВЫ КООРДИНАТЫ. Контрольная № 3 Геометрия 9 класс.Скачать

УРАВНЕНИЯ ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ НА ПЛОСКОСТИ

Геометрические объекты в аналитической геометрии определяются как геометрическое место точек, координаты которых в некоторой системе координат, удовлетворяют одному или системе уравнений, т.е. геометрическая задача сводится к алгебраической. Простейшими геометрическими объектами являются линейные объекты, которые задаются одним или системой линейных уравнений ( т.е. содержащие координаты точек в первой степени).

Рассмотрим сначала линейные объекты на плоскости, к которым относятся прямая и точка как пересечение двух прямых

Виды уравнений прямой на плоскости:

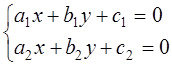
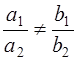
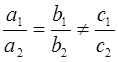
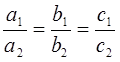
Общее уравнение прямой. A x+B у+C = 0 – общее уравнения прямой на плоскости. Система двух линейных уравнений с геометрической точки зрения представляет уравнения двух прямых на плоскости. При этом можно рассматривать три случая:1)прямые пересекаются и решение системы определяет единственную точку пересечения (линейный объект); 2) прямые параллельны и система не имеет решения; 3)прямые совпадают, система имеет бесчисленное множество решений

Теорема: Пусть дано общее уравнение прямой Ах+By+C=0 (1), где A, B одновременноне равны нулю, то плоский вектор n=(A,B) ортоганален прямой заданной уравнением (1) и поэтому называется нормальным вектором прямой.

Доказательство: подставим координаты точки М₀ лежащей в плоскости в уравнение (1) и получим Ах₀+By₀+C=0 (1¢). Вычтем (1)–(1¢) получим А(х–х₀)+B(y–y₀)=0. Если вектор М₀М=(х–х₀, y–y₀), то слева в полученном равенстве записано скалярное произведение векторов, оно равно 0, значит n и M₀M ортоганальны, следовательно вектор n ортогонален прямой. Вектор n=(A,B) называется нормальным вектором прямой.

Замечание: Пусть уравнения А₁х+B₁y+C₁=0 и А₂х+B₂y+C₂=0 определяют одну и ту же прямую, тогда найдется такое действительное число t, что А₁=t . А₂ и В₁=t . В₂ ,т.о нормальный вектор определяется не однозначно , он лишь задает перпендикулярное прямой направление.

Кроме общее уравнение прямой часто используются при решении задач другие виды уравнений прямой

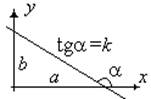
2) у= kx+ b -уравнение с угловым коэффициентом k и cмещением b; Угловым коэффициентом прямой, не параллельной оси ОУ называется число k, равное tga угла, на который нужно повернуть против часовой стрелки положительную часть оси ОХ, чтобы она стала параллельной данной прямой. С помощью углового коэффициента k можно легко определить угол между прямыми j= j₂–j₁ tgj =(k₂ —k₂)/(1+k₁k₂). Для перпендикулярных прямых: 1+k₁k₂=0 Для параллельных прямых: k₁=k₂.

3) -уравнение прямой в отрезках, где (а, b )- отрезки, отсекаемые на осях координат (c учетом знака). Геом.смысл: прямая отсекает на осях координат отрезки а и b

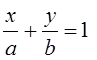
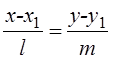
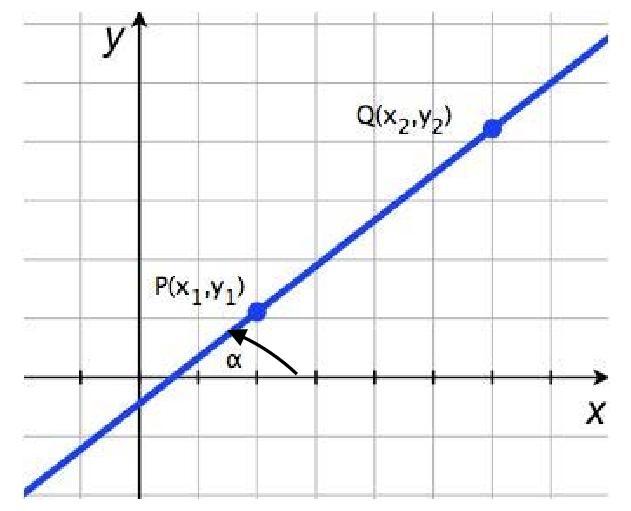
4) Каноническое уравнение прямой Пусть на прямой задана точка M₁(х₁;y₁)и направляющий. вектор прямой (параллельный прямой) а(l, m). Возьмем на прямой произвольную точку. М и вектор лежащий на прямой M₁М=(х–х₁; y–y₁), который параллелен направляющему вектору а(l, m) и поэтому координаты векторов пропорциональны.

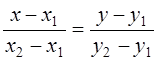
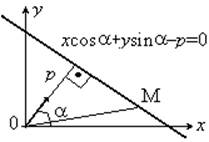
5) Уравнение прямой проходящей через две точки А(х₁, у₁) и В(х₂, у₂). Пусть на прямой заданы две точки М₁(x₁;y₁) и М₂(x₂;y₂). Т.к. на прямой заданы две точки, то задан направляющий вектор а (x₂–x₁; y₂–y₁)

6). Нормальное уравнениее прямой. xcosa+ysina–р=0 (ОР – перпендикулярный вектор из начала координат к прямой |ОР|= р>0 – расстояние от прямой до начала координат,a – угол между вектором ОР и положительным напр. оси ОХ.

Параметрическое уравнение прямой.

Прямая на плоскости частный случай прямой в пространстве.

У прямой в пространстве нет понятия нормального вектора.

Определение: если хотя бы один из коэффициентов в уравнении (1) =0, то уравнение называется неполным.

1. С=0, Ах+By=0 – проходит через (0,0)

2. С=0, А=0, By=0, значит у=0

3. С=0, B=0, Ах=0, значит х=0

4. А=0, By+C=0, паралл. ОХ

5. B=0, Ах+C=0, паралл. OY

j, – угол наклона прямой. tg угла наклона называется угловым коэффициентом прямой k=tg j,

Задача: записать уравнение прямой , если изветны р и a

Решение: Выделим на прямой ОР вектор ед. длины n. (|n|=1, n=(cosa, sina)). Пусть М(x,y) – произв.точка прямой. Рассмотрим два вектора n и ОМ. Найдем двумя способвами их скал.произведение. 1. ОМ . n=|OM| . |n|cosÐMOP=р. 2. ОМ . n=cosax+sinay. Приравняем правые части.

Задача: прямая задана общим ур–ем Ах+By+C=0. Перейти к норм. виду. xcosa+ysina–p=0

т.к. уравнения определяют одну прямую, то сущ. коэфф. пропорциональности.

cos 2 a+sin 2 a=t 2 (A 2 +B 2 ), t 2 =1/A 2 +B 2 , t=±(1/ A 2 +B 2 ). Sign t= – sign C

Что бы найти нормальное уравнение прямой нужно общее ур–е умножить на t.

Аtх+Bty+Ct=0, t–нормирующий множитель.

НОРМАЛЬНОЕ УРАВНЕНИЕ ПРЯМОЙ. Расстояние от точки до прямой.

1. xcosa+ysina–p=0

a – угол между вектором ОР и положительным напр. оси ОХ.

Задача: записать ур–е прямой , если изветны р и a

Решение: Выделим на прямой ОР вектор ед. длины n. |n|=1, n=(cosa, sina). Пусть М(x,y) – произв.точка прямой. Рассмотрим два вектора `n и `ОМ. Найдем двумя способвами их скал.произведение.

Задача: прямая задана общим ур–ем. Перейти к норм. виду.

т.к. уравнения определяют одну прямую, то сущ. коэфф. пропорциональности.

cos 2 a+sin 2 a=t 2 (A 2 +B 2 ), t 2 =1/A 2 +B 2 , t=±sqrt(1/ A 2 +B 2 ). Sign t= – sign C

Что бы найти нормальное уравнение прямой нужно общее ур–е умножить на t.

Аtх+Bty+Ct=0, t–нормирующий множитель.

2. Обозначим d – расстояние от точки до прямой, а ч/з б – отклонение точки от прямой. б=d, если нач.коорд. и точка по разные стороны; = – d, если нач.коорд. и точка по одну сторону.

Теорема: Пусть задано нормальное уравнение прямой xcosa+ysina–P=0 и М₁(x₁;y₁), тогда отклонение точки М₁ = x₁cosa+y₁sina–P=0

Задача: найти расстояние от точки М₀(x₀;y₀) до прямой Ах+By+C=0. Т.к. d=|d|, то формула расстояний принимает

Видео:9 класс. Геометрия. Декартовы координаты. Уравнение окружности. Уравнение прямой. Урок #6Скачать

Общее уравнение плоскости : описание, примеры, решение задач

В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.

Видео:Координаты на плоскости и в пространстве. Вебинар | МатематикаСкачать

Общее уравнение плоскости: основные сведения

Перед началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат O x y z в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x , y , и z , которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным.

Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.

Любую плоскость, заданную в прямоугольной системе координат O x y z трехмерного пространства, можно определить уравнением A x + B y + C z + D = 0 . В свою очередь, любое уравнение A x + B y + C z + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A , B , C , D – некоторые действительные числа, и числа A , B , C не равны одновременно нулю.

Теорема состоит из двух частей. Разберем доказательство каждой из них.

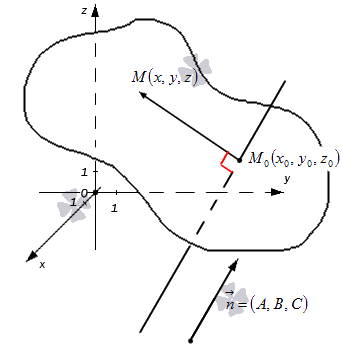
1. Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида A x + B y + C z + D = 0 . Допустим, задана некоторая плоскость и точка M 0 ( x 0 , y 0 , z 0 ) , через которую эта плоскость проходит. Нормальным вектором этой плоскости является n → = ( A , B , C ) . Приведем доказательство, что указанную плоскость в прямоугольной системе координат O x y z задает уравнение A x + B y + C z + D = 0 .

Возьмем произвольную точку заданной плоскости M ( x , y , z ) .В таком случае векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:

n → , M 0 M → = A x — x 0 + B ( y — y 0 ) + C ( z — z 0 ) = A x + B y + C z — ( A x 0 + B y 0 + C z 0 )

Примем D = — ( A x 0 + B y 0 + C z 0 ) , тогда уравнение преобразуется в следующий вид: A x + B y + C z + D = 0 . Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.

1. Во второй части теоремы утверждается, что любое уравнение вида A x + B y + C z + D = 0 задает некоторую плоскость в прямоугольной системе координат O x y z трехмерного пространства. Докажем это.

В теореме также указано, что действительные числа А , B , C одновременно не являются равными нулю. Тогда существует некоторая точка M 0 ( x 0 , y 0 , z 0 ) , координаты которой отвечают уравнению A x + B y + C z + D = 0 , т.е. верным будет равенство A x 0 + B y 0 + C z 0 + D = 0 . Отнимем левую и правую части этого равенства от левой и правой частей уравнения A x + B y + C z + D = 0 . Получим уравнение вида

A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 , и оно эквивалентно уравнению A x + B y + C z + D = 0 . Докажем, что уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает некоторую плоскость.

Уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n → = ( A , B , C ) и M 0 M → = x — x 0 , y — y 0 , z — z 0 . Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 множество точек M ( x , y , z ) задает плоскость, у которой нормальный вектор n → = ( A , B , C ) . При этом плоскость проходит через точку M ( x 0 , y 0 , z 0 ) . Иначе говоря, уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает в прямоугольной системе координат O x y z трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение A x + B y + C z + D = 0 также определяет эту плоскость. Теорема доказана полностью.

Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства.

Допустим, задано некоторое общее уравнение плоскости λ · A x + λ · B y + λ · C z + λ · D = 0 , где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением A x + B y + C z + D = 0 , поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства.

Раскроем чуть шире смысл теорем.

В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида A x + B y + C z + D = 0 ( при конкретных значениях чисел A , B , C , D ). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат.

Укажем пример как иллюстрацию этих утверждений.

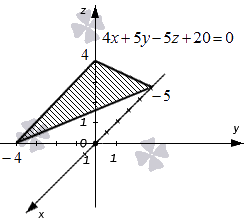
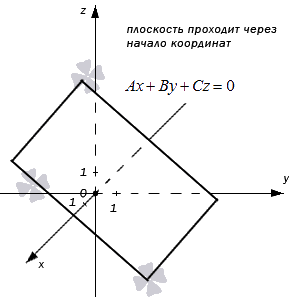
Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4 x + 5 y – 5 z + 20 = 0 , и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4 x + 5 y – 5 z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость.

Видео:Лекция 22. Декартова система координат на плоскости и полярная система координатСкачать

Общее уравнение плоскости, проходящей через точку

Повторимся: точка M 0 ( x 0 , y 0 , z 0 ) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением A x + B y + C z + D = 0 в том случае, когда подставив координаты точки M 0 ( x 0 , y 0 , z 0 ) в уравнение A x + B y + C z + D = 0 , мы получим тождество.

Заданы точки M 0 ( 1 , — 1 , — 3 ) и N 0 ( 0 , 2 , — 8 ) и плоскость, определяемая уравнением 2 x + 3 y — z — 2 = 0 . Необходимо проверить, принадлежат ли заданные точки заданной плоскости.

Решение

Подставим координаты точки М 0 в исходной уравнение плоскости:

2 · 1 + 3 · ( — 1 ) — ( — 3 ) — 2 = 0 ⇔ 0 = 0

Мы видим, что получено верное равенство, значит точка M 0 ( 1 , — 1 , — 3 ) принадлежит заданной плоскости.

Аналогично проверим точку N 0 . Подставим ее координаты в исходное уравнение:

2 · 0 + 3 · 2 — ( — 8 ) — 2 = 0 ⇔ 12 = 0

Равенство неверно. Таким, образом, точка N 0 ( 0 , 2 , — 8 ) не принадлежит заданной плоскости.

Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.

Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n → = ( A , B , C ) — нормальный вектор для плоскости, определяемой уравнением A x + B y + C z + D = 0 . Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.

В прямоугольной системе координат задана плоскость 2 x + 3 y — z + 5 = 0 . Необходимо записать координаты всех нормальных векторов заданной плоскости.

Решение

Мы знаем, что заданные общим уравнением коэффициенты при переменных x , y , z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n → исходной плоскости имеет координаты 2 , 3 , — 1 . В свою очередь, множество нормальных векторов запишем так:

λ · n → = λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0

Ответ: λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0

Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.

Очевидным фактом является то, что нормальный вектор n → = ( A , B , C ) является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M 0 ( x 0 , y 0 , z 0 ) , принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.

Общее уравнение плоскости с нормальным вектором n → = ( A , B , C ) будет выглядеть так: A x + B y + C z + D = 0 . По условию задачи точка M 0 ( x 0 , y 0 , z 0 ) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство: A x 0 + B y 0 + C z 0 + D = 0

Вычитая соответственно правые и левые части исходного уравнения и уравнения A x 0 + B y 0 + C z 0 + D = 0 , получим уравнение вида A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 . Оно и будет уравнением плоскости, проходящей через точку M 0 ( x 0 , y 0 , z 0 ) и имеющей нормальный вектор n → = ( A , B , C ) .

Возможно получить это уравнение другим способом.

Очевидным фактом является то, что все точки М ( x , y , z ) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:

n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0

Задана точка М 0 ( — 1 , 2 , — 3 ) , через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n → = ( 3 , 7 , — 5 ) . Необходимо записать уравнение заданной плоскости.

Решение

Рассмотрим два способа решения.

1. Исходные условия позволяют получить следующие данные:

x 0 = — 1 , y 0 = 2 , z 0 = — 3 , A = 3 , B = 7 , C = — 5

Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0

3 ( x — ( — 1 ) ) + 7 ( y — 2 ) — 5 ( z — ( — 3 ) ) = 0 ⇔ 3 x + 7 y — 5 z — 26 = 0

1. Допустим, М ( x , y , z ) – некоторая точки заданной плоскости. Определим координаты вектора M 0 M → по координатам точек начала и конца:

M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) = ( x + 1 , y — 2 , z + 3 )

Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:

n → , M 0 M → = 0 ⇔ 3 ( x + 1 ) + 7 ( y — 2 ) — 5 ( z + 3 ) = 0 ⇔ ⇔ 3 x + 7 y — 5 z — 26 = 0

Ответ: 3 x + 7 y — 5 z — 26 = 0

Видео:Координаты вектора. 9 класс.Скачать

Неполное общее уравнение плоскости

Выше мы говорили о том, что, когда все числа А , B , C , D отличны от нуля, общее уравнение плоскости A x + B y + C z + D = 0 называют полным. В ином случае общее уравнение плоскости является неполным.

Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.

1. В случае, когда D = 0 , мы получаем общее неполное уравнение плоскости: A x + B y + C z + D = 0 ⇔ A x + B y + C z = 0

Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О ( 0 , 0 , 0 ) , то придем к тождеству:

A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0

1. Если А = 0 , В ≠ 0 , С ≠ 0 , или А ≠ 0 , В = 0 , С ≠ 0 , или А ≠ 0 , В ≠ 0 , С = 0 , то общие уравнения плоскостей имеют вид соответственно: B y + C z + D = 0 , или A x + C z + D = 0 , или A x + B y + D = 0 . Такие плоскости параллельны координатным осям О x , O y , O z соответственно. Когда D = 0 , плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей B y + C z + D = 0 , A x + C z + D = 0 и A x + B y + D = 0 задают плоскости, которые перпендикулярны плоскостям O y z , O x z , O z y соответственно.

1. При А = 0 , В = 0 , С ≠ 0 , или А = 0 , В ≠ 0 , С = 0 , или А ≠ 0 , В = 0 , С = 0 получим общие неполные уравнения плоскостей: C z + D = 0 ⇔ z + D C = 0 ⇔ z = — D C ⇔ z = λ , λ ∈ R или B y + D = 0 ⇔ y + D B = 0 ⇔ y = — D B ⇔ y = λ , λ ∈ R или A x + D = 0 ⇔ x + D A = 0 ⇔ x = — D A ⇔ x = λ , λ ∈ R соответственно.

Эти уравнения определяют плоскости, которые параллельны координатным плоскостям O x y , O x z , O y z соответственно и проходят через точки 0 , 0 , — D C , 0 , — D B , 0 и — D A , 0 , 0 соответственно. При D = 0 уравнения самих координатных плоскостей O x y , O x z , O y z выглядят так: z = 0 , y = 0 , x = 0

Задана плоскость, параллельная координатной плоскости O y z и проходящая через точку М 0 ( 7 , — 2 , 3 ) . Необходимо составить общее уравнение заданной плоскости.

Р​​ешение

У​​​​​словием задачи определено, что заданная плоскость параллельна координатной плоскости O y z , а, следовательно, может быть задана общим неполным уравнением плоскости A x + D = 0 , A ≠ 0 ⇔ x + D A = 0 . Поскольку точка M 0 ( 7 , — 2 , 3 ) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x + D A = 0 , иначе говоря, должно быть верным равенство 7 + D A = 0 . Преобразуем: D A = — 7 , тогда требуемое уравнение имеет вид: x — 7 = 0 .

Задачу возможно решить еще одним способом.

Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости O y z . Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости O y z : i → = ( 1 , 0 , 0 ) . Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:

A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 ⇔ ⇔ 1 · ( x — 7 ) + 0 · ( y + 2 ) + 0 · ( z — 3 ) = 0 ⇔ ⇔ x — 7 = 0

Ответ: x — 7 = 0

Задана плоскость, перпендикулярная плоскости O x y и проходящая через начало координат и точку М 0 ( — 3 , 1 , 2 ) .

Решение

Плоскость, которая перпендикулярна координатной плоскости O x y определяется общим неполным уравнением плоскости A x + B y + D = 0 ( А ≠ 0 , В ≠ 0 ) . Условием задачи дано, что плоскость проходит через начало координат, тогда D = 0 и уравнение плоскости принимает вид A x + B y = 0 ⇔ x + B A y = 0 .

Найдем значение B A . В исходных данных фигурирует точка М 0 ( — 3 , 1 , 2 ) , координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: — 3 + B A · 1 = 0 , откуда определяем B A = 3 .

Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x + 3 y = 0 .

Видео:Составить уравнение прямой, проходящей через две данные точки. Метод координат. Геометрия 9 классСкачать

Способы задавания уравнений прямых в плоскости и в трехмерном пространстве

Прямая является основным геометрическим объектом на плоскости и в трехмерном пространстве. Именно из прямых строятся многие фигуры, например: параллелограмм, треугольник, призма, пирамида и так далее. Рассмотрим в статье различные способы задавания уравнений прямых.

Видео:Уравнения координатных осейСкачать

Определение прямой и виды уравнений для ее описания

Каждый школьник хорошо себе представляет, о каком геометрическом объекте идет речь. Прямую можно представить как совокупность точек, причем если соединить каждую из них по очереди со всеми остальными, то мы получим набор параллельных векторов. Иными словами, попасть в каждую точку прямой можно из одной фиксированной ее точки, перенося ее на некоторый единичный вектор, умноженный на действительное число. Это определение прямой используется для задавания векторного равенства для ее математического описания как на плоскости, так и в трехмерном пространстве.

Вам будет интересно: Муляж — это необходимость или выдумка?

Прямая может быть математически представлена следующими видами уравнений:

• общее;
• векторное;
• параметрическое;
• в отрезках;
• симметричное (каноническое).

Далее рассмотрим все названные виды и покажем на примерах решения задач, как с ними работать.

Видео:Аналитическая геометрия на плоскостиСкачать

Векторное и параметрическое описание прямой

Вам будет интересно: Размер бумаги А3 в сантиметрах и не только: краткий путеводитель

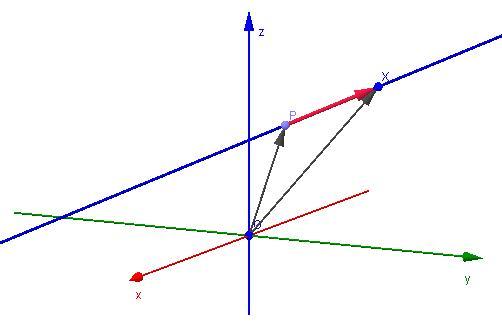
Начнем с задавания прямой через известный вектор. Предположим, что в пространстве имеется фиксированная точка M(x0; y0; z0). Известно, что прямая проходит через нее и направлена вдоль векторного отрезка v¯(a; b; c). Как по этим данным найти произвольную точку прямой? Ответ на этот вопрос даст следующее равенство:

(x; y; z) = (x0; y0; z0) + λ * (a; b; c)

Где λ — произвольное число.

Аналогичное выражение можно записать для двумерного случая, где координаты векторов и точек представлены набором из двух чисел:

(x; y) = (x0; y0) + λ * (a; b)

Записанные уравнения называются векторными, а сам направленный отрезок v¯ — это направляющий вектор для прямой.

Из записанных выражений соответствующие параметрические уравнения получаются просто, достаточно лишь переписать их в явном виде. Например, для случая в пространстве получаем следующее уравнение:

С параметрическими уравнениями удобно работать, если необходимо проанализировать поведение каждой координаты. Заметим, что хотя параметр λ может принимать произвольные значения, но во всех трех равенствах он должен быть одинаковым.

Видео:Математика 6 класс (Урок№79 - Декартова система координат на плоскости.)Скачать

Общее уравнение

Другим способом задавания прямой, который часто используют для работы с рассматриваемым геометрическим объектом, является применение уравнения общего вида. Для двумерного случая оно имеет вид:

A * x + B * y + C = 0

Здесь большие латинские буквы представляют конкретные числовые значения. Удобство данного равенства при решении задач заключается в том, что оно в явном виде содержит вектор, который перпендикулярен прямой. Если обозначить его n¯, тогда можно записать:

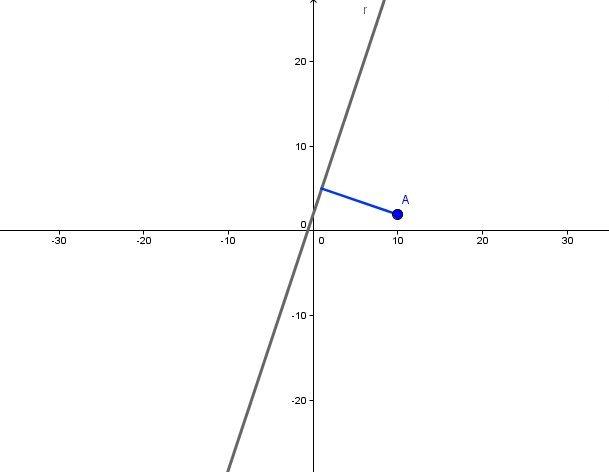
Кроме того, выражение удобно применять для определения расстояния от прямой до некоторой точки P(x1; y1). Формула для расстояния d имеет вид:

d = |A * x1 + B * y1 + C| / √(A2 + B2)

Несложно показать, что если из общего уравнения выразить явно переменную y, то получится следующая известная форма записи прямой:

Где k и b однозначно определяются числами A, B, C.

Видео:Векторный метод в стереометрии. Задача 14 профильный ЕГЭСкачать

Уравнение в отрезках и каноническое

Уравнение в отрезках проще всего получить из общего вида. Покажем, как это можно сделать.

Предположим, что имеется следующая прямая:

A * x + B * y + C = 0

Перенесем свободный член в правую часть равенства, затем поделим на него все уравнение, получаем:

x / (-C / A) + y / (-C / B) = 1;

x / q + y / p = 1, где q = -C / A, p = -C / B

Мы получили так называемое уравнение в отрезках. Свое название оно получило по причине того, что знаменатель, на который делится каждая переменная, показывает значение координаты пересечения прямой с соответствующей осью. Этот факт удобно использовать для изображения прямой в координатной системе, а также для анализа ее взаимного расположения по отношению к другим геометрическим объектам (прямым, точкам).

Теперь перейдем к получению канонического уравнения. Это проще сделать, если рассмотреть параметрический вариант. Для случая на плоскости имеем:

Выразим параметр λ в каждом равенстве, затем приравняем их, получаем:

(x — x0) / a = (y — y0) / b

Это и есть искомое уравнение, записанное в симметричной форме. Так же, как и векторное выражение, оно в явной форме содержит координаты направляющего вектора и координаты одной из точек, которая принадлежит прямой.

Можно заметить, что в данном пункте мы привели уравнения для двумерного случая. Аналогичным образом можно составить уравнение прямой в пространстве. Здесь нужно заметить, что если каноническая форма записи и выражение в отрезках будут иметь такой же вид, то общее уравнение в пространстве для прямой представляется системой из двух уравнений для пересекающихся плоскостей.

Видео:Координатная плоскость. Часть 1 #shortsСкачать

Задача на построение уравнения прямой

Из геометрии каждый школьник знает, что через две точки можно начертить единственную линию. Предположим, что в координатной плоскости заданы следующие точки:

Следует найти уравнение прямой, которой принадлежат обе точки, в отрезках, в векторном, каноническом и в общем виде.

Получим сначала векторное уравнение. Для этого следует определить для прямой направляющий вектор M1M2¯:

M1M2¯ = (-1; 3) — (1; 2) = (-2; 1)

Теперь можно составить векторное уравнение, взяв одну из двух заданных в условии задачи точек, например, M2:

(x; y) = (-1; 3) + λ * (-2; 1)

Чтобы получить каноническое уравнение, достаточно преобразовать найденное равенство в параметрический вид и исключить параметр λ. Имеем:

x = -1 — 2 * λ, следовательно, λ = x + 1 / (-2);

y = 3 + λ, далее получаем λ = y — 3;

x + 1 / (-2) = (y — 3) / 1

Оставшиеся два уравнения (общее и в отрезках) можно найти из канонического, преобразуя его следующим образом:

общее уравнение: x + 2 * y — 5 = 0;

в отрезках уравнение: x / 5 + y / 2,5 = 1

Полученные уравнения показывают, что вектор (1; 2) должен быть перпендикулярен прямой. Действительно, если найти его скалярное произведение с направляющим вектором, то оно будет равно нулю. Уравнение в отрезках говорит, что прямая пересекает ось x в точке (5; 0), а ось y — в точке (2,5; 0).

Видео:Полярная система координатСкачать

Задача на определение точки пересечения прямых

На плоскости заданы две прямые следующими уравнениями:

(x; y) = (0; -1) + λ * (-1; 3)

Необходимо определить координаты точки, в которой эти прямые пересекаются.

Решить задачу можно двумя способами:

Не выполнять никаких преобразований, а просто подставить координату точки пересечения, выраженную через параметр λ, в первое уравнение. Затем найти значение параметра.

Поступим вторым способом. Имеем:

2 * (-λ) + (-1) + 3 * λ — 1 = 0;

Подставляем полученное число в векторное уравнение:

(x; y) = (0; -1) + 2 * (-1; 3) = (-2; 5)

Таким образом, единственной точкой, которая принадлежит обеим прямым, является точка с координатами (-2; 5). В ней прямые пересекаются.

🎦 Видео

ВПР / 6 класс. Определить координаты точекСкачать

УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать

Симметрия точек на координатной плоскостиСкачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Метод координат для ЕГЭ с нуля за 30 минут.Скачать

Введение в аналитическую геометрию. Треугольник в системе координатСкачать

Аналитическая геометрия на плоскостиСкачать