Принцип оптимальности Беллмана позволяет решать или осмыслить многие интересные задачи, возникающие в реальной жизни, например, задачу о рациональной эксплуатации генерирующего предприятия (ТЭЦ, ГЭС), выбора экономичного состава агрегатов и др.
При эксплуатации гидростанций и тепловых станций возникает необходимость периодической остановки агрегатов при снижении нагрузки и включения агрегатов, находящихся в резерве, когда нагрузка увеличивается. Включение в работу определенных агрегатов влияет на величину и размещение резервов системы, на режим электрической сети, на перетоки по межсистемным линиям электропередачи, на расход топлива и тд.
Если на станциях имеется n агрегатов и каждый из них может быть либо включен, либо отключен, то все множество всех вариантов для работы с любой мощностью составит 2 в степени n.
Даже для n = 50 число вариантов становится очень большим!
В общем виде такие задачи являются нелинейными, целочисленными, многоэкстремальными, на состав агрегатов влияет режим электрических сетей, который следует оценивать и прогнозировать статистическими методами. Для решения таких задач обычный математический аппарат не подходит.
В частном случае методы динамического программирования позволяют решать подобные задачи при числе агрегатов порядка 20-30.
Приведем примеры задач, в которых принцип динамического программирования эффективно работает и позволяет найти оптимальное решение.
Задача о графике эксплуатации электростанция. Станция имеет L агрегатов, известна производительность одного агрегата и цена единицы произведенной электроэнергии.
Задан график оплаченной электроэнергии, избыточно произведенная электроэнергия не оплачивается.
Известны затраты на поддержание в рабочем агрегатов, затраты на консервацию и затраты на пуск. Требуется определить оптимальный режим эксплуатации.
Интересны задачи о распределении инвестиций и ресурсов.
Задача о распределении инвестиций: имеется несколько предприятий, между которыми требуется распределить данную сумму инвестиций. Известна эффективность вложения данной суммы средств в каждое предприятие.
Задача о распределении ресурса: имеется N предприятий, каждое из которых приносит доход, зависящий от доли выделенного ресурса. Требуется наилучшим способом распределить между ними ограниченный ресурс a на доли x1, . , xN (x1 ≥ 0, . , xN ≥ 0, x1 +. + xN ≤ a).
Задача о наилучшей загрузке транспорта: транспорт, имеющее грузоподъемность a , загружается грузами N типов. Каждый тип груза имеет стоимость yi и вес zi .
Требуется найти оптимальный вариант загрузки, при котором стоимость взятых на борт предметов максимальна.
Задача о замене автомобиля: автотранспортное предприятие планирует приобрести автомобиль и эксплуатировать его в течение N лет.
Можно либо купить новый автомобиль возраста x0 = 0 лет и стоимости p, либо бывший в эксплуатации возраста x0 > 0 лет по стоимости, зависящей от времени эксплуатации.
Показатели эксплуатации автомобиля включают: f (t) – стоимость произведенных за год изделий на оборудовании возраста t лет; r(t) – затраты на эксплуатацию в течение года автомобиля возраста t.
В процессе эксплуатации автомобиль можно продавать по ликвидной стоимости и купить новый. В конце срока эксплуатации автомобиль также продается по ликвидной стоимости. Определить оптимальный возраст автомобиля при покупке и оптимальный график его замены.
Все эти и многие другие задачи могут быть решены с помощью принципа оптимальности Беллмана.
Опишем формально принцип Беллмана и объясним его смысл.
Ключевым является понятие управляемого объекта, к которому применяется принцип Беллмана.
Пусть имеется изменяющийся во времени объект, на который осуществляется внешнее воздействие u(t) или управление, а x(t) – описание этого объекта в момент времени t.
Если при известном управлении до момента t1, зная описание x(t) в момент времени t , можно однозначно определить его значение x(t) для любого t > t1 , то такое описание называют полным.
Полное описание называют состоянием, множество возможных состояний – пространством состояний.
Сам объект, допускающий возможность полного описания, называют динамической системой.
Будем рассматривать только дискретные моменты времени и в эти моменты управлять системой.
Каждому переходу из состояния xk в следующее состояние ставится в соответствие функция затрат, зависящая от состояния xk , момента времени и применяемого управления.
Требуется найти такое начальное состояние и такой допустимый набор управлений, переводящий систему в одно из конечных состояний, чтобы общие затраты, являющиеся аддитивной функцией затрат на отдельных шагах, были минимальны.
Итак, на каждом шаге мы вносим плату за выбранное управление, далее плата, внесенная на каждом шаге, суммируется и подводится итог.
Мы желаем таким образом управлять объектом, чтобы общая сумма затрат была минимальной.
Это и есть общая постановка задачи динамического программирования или управления динамической системой.
Иными словами, нам нужна программа действий на каждом шаге, позволяющий минимизировать затраты.
Общий принцип формулируется так: вне зависимости от того, каким образом управляемый процесс на шаге k попал в состояние xk , далее надо применять управление, оптимальное для этого состояния в завершающем (N − k)-шаговом процессе с учетом оптимального продолжения.
Это одна из возможных формулировок принципа Беллмана в форме достаточного условия.
Пусть Yk – множество состояний, из которых (при использовании допустимых управлений) можно ровно за k шагов попасть в одно из состояний финального множества X N.
Можно считать, что Y0 = X N.
Возьмем произвольное xN −k ∈Yk и обозначим через Sk (xN −k ) функцию, описывающую зависимость оптимальных затрат от состояния xN −k за k последних шагов, переводящих систему из xN −k в X N.
Такие функции называют функциями Беллмана.
Поскольку для состояний xN −1 из множества Y1 переход в XN происходит за один шаг, то функция оптимальных затрат S1(xN −1) может быть записана следующим образом:
Второе ограничение необходимо для того, чтобы гарантировать достижение заданного финального множества X N.
Значение uN , при котором достигается минимум в этом соотношении, обозначим через u*N( xN-1).
Несложно понять (сделайте это!), что функция оптимальных затрат Sk +1(xN −k −1) каждой следующей задачи рекуррентно выражается через предыдущую Sk (xN −k )
u*N −k (xN −k – 1) – управление, при котором достигается минимум затрат в (2).
Выражение u*k (xk-1) − определяет для каждого момента времени оптимальные правила управления в виде функций от текущего состояния динамического процесса, задают закон оптимального управления в форме оптимального регулятора по состоянию.
Оптимальное начальное состояние x*0 можно получить из решения следующей задачи:
Систему (1)-(3) называют рекуррентными уравнениями Беллмана.
Значения оптимального управления в явном виде можно последовательно определить следующим образом:
Стартуем из начального состояния x0.
Видео:Видео Лекция 9-1 МОР МПУР Динамическое Программирование Задача оптимального распределения инвестицийСкачать

Усиление обучения: Марков-процесс принятия решений (часть 2)
Дата публикации Aug 30, 2019
Эта история в продолжение предыдущего,Усиление обучения: Марков-процесс принятия решений (часть 1)история, в которой мы говорили о том, как определять MDP для данной среды. Мы также говорили о уравнении Беллмана, а также о том, как найти функцию Value и функцию Policy для состояния.В этой историимы собираемся сделать шагГлубжеи узнать оУравнение ожиданий Беллманакак мы находимоптимальное значениеа такжеОптимальная функция политикидля данного состояния, а затем мы определимУравнение оптимальности Беллмана,
Давайте кратко рассмотрим эту историю:
- Уравнение ожиданий Беллмана
- Оптимальная политика
- Уравнение Беллмана для функции состояния
- Уравнение оптимальности Беллмана для функции значения состояния-действия
Так что, как всегда, берите свой кофе и не останавливайтесь, пока вы не гордитесь ».
Давайте начнем с,Что такое уравнение ожидания Беллмана?
Видео:Принцип оптимальности БеллманаСкачать

Уравнение ожиданий Беллмана
Быстрый обзорУравнение Беллманамы говорили в предыдущей истории:
Из вышесказанногоуравнениемы можем видеть, что значение состояния может бытьразложившийсяв немедленное вознаграждение (R [T + 1])плюсзначение государства-преемника (v [S (t + 1)]) с учетом скидки (γ). Это все еще означает уравнение ожиданий Беллмана. Но теперь то, что мы делаем, мы находим ценность определенного государстваподвергаетсяк какой-то политике (π). В этом разница между уравнением Беллмана и уравнением ожиданий Беллмана.
Математически мы можем определить уравнение ожиданий Беллмана как:
Давайте назовем это уравнение 1. Вышеупомянутое уравнение говорит нам, что ценность определенного состояния определяется немедленным вознаграждением плюс значение состояний-преемников, когда мы следуем определенной политике (π),
Точно так же мы можем выразить нашу функцию Value-action-состояния (Q-Function) следующим образом:
Давайте назовем это уравнение 2. Из приведенного выше уравнения мы можем видеть, что значение состояния-действия состояния может быть разложено нанемедленная наградамы выполняем определенное действие в состоянии (s) и переезд в другое состояние (s’) плюс дисконтированная стоимость состояния-действия государства (s’)в отношениинекоторые действия ( ) наш агент возьмет из этого штата подопечных.
Идем глубже в уравнение ожиданий Беллмана:
Во-первых, давайте разберемся с уравнением ожидания Беллмана для функции состояния-состояния с помощью резервной диаграммы:
Эта резервная диаграмма описывает значение нахождения в определенном состоянии. Из состояния s есть некоторая вероятность того, что мы предпримем оба действия. Для каждого действия существует Q-значение (функция значения действия состояния). Мы усредняем Q-значения, которые говорят нам, насколько хорошо быть в определенном состоянии. В основном, это определяет Vπ (s). [Смотрите уравнение 1]
Математически мы можем определить это следующим образом:
Это уравнение также говорит нам о связи между функцией State-Value и функцией Value-Action Value.
Теперь давайте посмотрим на схему резервного копирования для функции значения состояния-действия:
Эта резервная диаграмма говорит, что предположим, что мы начнем с некоторых действий (а). Таким образом, из-за действия (а) агент может попасть в любое из этих состояний окружающей средой. Поэтому мы задаем вопрос,Насколько хорошо действовать (а)?
Мы снова усредняем значения состояний обоих состояний, добавленные с немедленной наградой, которая говорит нам, насколько хорошо выполнить определенное действие (а). Это определяет наш qπ (S, A).
Математически мы можем определить это следующим образом:
где P — вероятность перехода.
Теперь давайте соединим эти резервные диаграммы вместе, чтобы определить функцию состояния-значения, VП (с):
Из приведенной выше диаграммы, если наш агент в какой-тосостояния)и из этого состояния предположим, что наш агент может предпринять два действия, в зависимости от того, какая среда может перевести нашего агента в любую изсостояния (s’), Обратите внимание, что вероятность действий, которые наш агент может предпринять из штатаsвзвешивается нашей политикой и после принятия этого действия вероятность того, что мы приземлимся в любом из государств (s’) взвешивается окружающей средой
Теперь мы задаемся вопросом: насколько хорошо быть в состоянии (ях) после того, как вы предприняли какие-то действия и приземлились в другом (ых) государстве (ах) и следовали нашей политике (π) после того?
Это похоже на то, что мы делали раньше, мы собираемся усреднить значение преемников (s’) с некоторой вероятностью перехода (P), взвешенной с нашей политикой.
Математически мы можем определить это следующим образом:
Теперь, давайте сделаем то же самое для функции значения состояния действия, qπ (S, а):
Это очень похоже на то, что мы сделали вФункция значения состоянияи только она обратная, так что эта диаграмма в основном говорит о том, что наш агент предпринял какие-то действия ( ) из-за которого окружающая среда может посадить нас в любом из государств (s), то из этого состояния мы можем выбрать любые действия (а») взвешены с вероятностью нашей политики (π). Опять же, мы усредняем их вместе, и это дает нам понять, насколько хорошо предпринимать определенные действия в соответствии с определенной политикой (π) все это время.
Математически это можно выразить как:
Итак, вот как мы можем сформулировать уравнение ожиданий Беллмана для данного MDP, чтобы найти его функцию значения состояния и функцию значения состояния.Но это не говорит нам лучший способ вести себя в MDP, Для этого давайте поговорим о том, что подразумевается подОптимальное значениеа такжеОптимальная функция политики,
Видео:Динамическое программирование. Задача о распределении инвестиций.Скачать

Функция оптимального значения
Определение оптимальной функции состояния-значения
В среде MDP существует много различных функций-значений в соответствии с различными политиками.Функция оптимального значения — это та, которая дает максимальное значение по сравнению со всеми другими функциями значения., Когда мы говорим, что решаем MDP, это фактически означает, что мы находим функцию оптимального значения.
Итак, математически оптимальная функция состояния-значения может быть выражена как:
В приведенной выше формуле v ∗ (s) говорит нам, какое максимальное вознаграждение мы можем получить от системы.
Определение функции оптимального значения состояния-действия (Q-функция)
По аналогии,Функция оптимального значения состояния-действияговорит нам максимальное вознаграждение, которое мы собираемся получить, если мы находимся в состоянии s и предпринимаем соответствующие действия.
Математически, это может быть определено как:
Оптимальная функция состояния-значения: Это функция максимального значения для всех политик.
Функция оптимального значения состояния-действия: Это функция максимального значения действия для всех политик.
Теперь давайте посмотрим, что подразумевается под Оптимальной политикой?
Видео:Задача оптимального управления + пример решенияСкачать

Оптимальная политика
Прежде чем мы определим оптимальную политику, давайте знать,что подразумевается под одной политикой лучше, чем с другой политикой?
Мы знаем, что для любого MDP существует политика (π)лучше любой другой политики (π»). Но как?
Мы говорим, что одна политика (π)лучше другой политики (π») если значение функции с политикойπдля всех состояний больше значения функции с политикойπ»для всех государств. Интуитивно это можно выразить как:
Теперь давайте определимсяОптимальная политика:
Оптимальная политикаэто тот, который приводит к функции оптимального значения.
Обратите внимание, что в MDP может быть более одной оптимальной политики. Но,все оптимальные политики достигают одной и той же функции оптимального значения и функции значения оптимального состояния-действия (Q-функция),
Теперь возникает вопрос, как мы находим оптимальную политику.
Нахождение оптимальной политики:
Мы находим оптимальную политику путем максимизацииQ*(s, a), т.е. наша оптимальная функция значения состояния-действия. Мы решаем q * (s, a) и затем выбираем действие, которое дает нам наиболее оптимальную функцию значения состояния-действия (q * (s, a)).
Вышеприведенное утверждение может быть выражено как:
Это говорит о том, что для состояния s мы выбираем действие a с вероятностью 1, если оно дает нам максимум q * (s, a). Таким образом, если мы знаем q * (s, a), мы можем получить из него оптимальную политику.
Давайте разберемся с этим на примере:
В этом примере красные дуги являютсяоптимальная политикаэто означает, что если наш агент пойдет по этому пути, он будетприносить максимальное вознаграждениеиз этого МДП. Кроме того, увидевд *значения для каждого состояния мы можем сказать действия нашего агента, которые принесут максимальное вознаграждение. Таким образом, оптимальная политика всегда действует с более высоким значением q * (функция значения состояния-действия). Например, в состоянии со значением 8 есть q * со значениями 0 и 8. Наш агент выбирает тот, у которого большед *значение то есть 8.
Теперь возникает вопрос,Как мы находим эти значения q * (s, a)?
Именно здесь в игру вступает уравнение оптимальности Беллмана.
Видео:Поиск решения. Задача о выборе инвестицийСкачать

Уравнение оптимальности Беллмана
Функция оптимального значения рекурсивно связана с уравнением оптимальности Беллмана
Уравнение оптимальности Беллмана такое же, как и уравнение ожиданий Беллмана, но единственное отличие состоит в том, что вместо того, чтобы брать среднее значение действий, которые может выполнить наш агент, мы выполняем действие с максимальным значением.
Давайте разберемся с помощью диаграммы резервного копирования:
Предположим, наш агент находится в состоянии S, и из этого состояния он может выполнить два действия (a). Итак, мы смотрим на значения действий для каждого из действий иВ отличие от, Уравнение ожиданий Беллмана,вместоприниматьсреднийнаш агент принимает меры сбольшее значение q *, Это дает нам ценность быть в состоянии S.
Математически это можно выразить как:
Аналогично, давайте определим уравнение оптимальности Беллмана дляФункция значения состояния состояния (Q-функция),
Давайте посмотрим на схему резервного копирования для функции значения состояния-действия (Q-функция):
Предположим, наш агент совершил действие a в каком-то состоянии s. Теперь, на окружающей среде, что это может взорвать нас в любое из этих государств (s’). Мы по-прежнему берем среднее значение обоих государств, но единственноеразницанаходится в уравнении оптимальности Беллмана мы знаемоптимальные значениякаждого из состояний. В отличие от уравнения ожиданий Беллмана, мы просто знали значение состояний.
Математически это можно выразить как:
Давайте снова сшиваем эти резервные диаграммы для функции состояния-значения:
Предположим, наш агент находится в состоянии s, и из этого состояния он предпринял какое-то действие (a), когда вероятность совершения этого действиявзвешенныйполитикой. И из-за действия (а), агент может быть взорван в любом из состояний (s’) где вероятность взвешена окружающей средой.Чтобы найти значение состояния S, мы просто усредняем оптимальные значения состояний (s ’)., Это дает нам ценность пребывания в состоянии S.
Математически это можно выразить как:
Максимум в уравнении потому, что мы максимизируем действия, которые агент может предпринять в верхних дугах. Это уравнение также показывает, как мы можем связать функцию V * с самим собой.
Теперь давайте посмотрим на уравнение оптимальности Беллмана для функции значения состояния-действия, q * (s, a):
Предположим, наш агент был в состоянииsи потребовалось какое-то действие ( ). Из-за этого действия окружающая среда может высадить нашего агента в любой из штатов (s’) и из этих состояний мы получаемразворачиваниядействие, которое предпримет наш агент, то есть выбор действия смаксимальное значение q *, Мы поддерживаем это до самого верха, и это говорит нам о значении действия a.
Математически это можно выразить как:
Давайте посмотрим на пример, чтобы понять его лучше:
Посмотрите на красные стрелки, предположим, что мы хотим найтиценностьсостояния со значением 6 (в красном), как мы видим, мы получаем вознаграждение -1, если наш агент выбирает Facebook, и вознаграждение -2, если наш агент хочет учиться. Чтобы найти значение состояния в красном, мы будем использоватьУравнение Беллмана для функции состояниято естьучитывая, что два других состояния имеют оптимальное значение, мы возьмем среднее значение и максимизируем оба действия (выберите то, которое дает максимальное значение), Таким образом, из диаграммы мы можем видеть, что переход на Facebook дает значение 5 для нашего красного состояния, а при обучении — значение 6, а затем мы максимизируем два, что дает нам 6 в качестве ответа.
Теперь, как мы решаем уравнение оптимальности Беллмана для больших MDP. Для этого мы используемАлгоритмы динамического программированиянравитсяИтерация политикиЗначение итерации, которую мы рассмотрим в следующем рассказе и другие методы, такие какQ-Learningа такжеSarsaкоторые используются для изучения временных различий, о которых мы расскажем в будущем.
Поздравляю с таким большим успехом! 👍
Надеюсь, что эта история повышает ценность вашего понимания MDP. Хотелось бы связаться с вами на #Instagram,
Спасибо, что поделились со мной своим временем!
Если вам нравится этот, пожалуйста, дайте мне знать, нажав на 👏. Это помогает мне писать больше!
Видео:Правило 72 для расчёта удвоения инвестицийСкачать

Принцип оптимальности и рекуррентные соотношения Беллмана
Принцип оптимальности был сформулирован Беллманом в 1953г. Сформулируем его так, как было предложено Венцель (несколько отличным образом).
Рассмотрим n-й последний шаг: Sn-1 состояние системы к началу n-ого шага, Sn – конечное состояние, Хn – управление на n-ом шаге, а fn (Sn-1, Xk) – целевая функция (или как еще говорят – выигрыш) n-ого шага.
Согласно принципу оптимальности, Хn нужно выбирать так, чтобы для любых состояний Sn-1 получить максимум (или минимум – ограничимся задачей на максимум – это не принципиально) целевой функции на этом шаге. Каково бы ни было состояние S системы в результате какого-либо шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный.
Принцип оптимальности утверждает, что для любого процесса без обратной связи оптимальное управление таково, что оно является оптимальным для любого подпроцесса по отношению к исходному состоянию этого процесса. Поэтому решение на каждом шагу оказывается наилучшим с точки зрения управления в целом.
Рекуррентные соотношения Беллмана. Вместо исходной задачи с фиксированным числом шагов n и начальным состоянием S0 рассмотрим последовательность задач, полагая последовательно n = 1, 2, … при различных S – одношаговую, двухшаговую, и т.д. – используя принцип оптимизации.
На каждом шаге для любого состояния системы Sk-1решениеХk (управление) нужно выбирать «с оглядкой», так как этот выбор влияет на последующее состояние Sk и дальнейший процесс управления, зависящий от Sk.
Но есть один шаг, последний, который может для любого состояния Sn-1планировать локально-оптимально, исходя только из соображений этого последнего шага.
Обозначим через 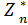

| < Хn>Хn> |

Максимизация ведется по всем допустимым управлениям Хn.
Решение Хn, при котором достигается 
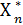
Решив одномерную задачу локальной оптимизации по уравнению (1), найдем для всех возможных состояний Sn-1 две функции 
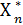
Рассмотрим теперь двух шаговую задачу: присоединим к n-ому шагу (n-1) ша .
Для любых состояний Sn-2, произвольных уравнений Хn-1 и оптимальном уравнении на n-ом шаге значение целевой функции на двух последних шагах равно
fn-1 (Sn-2, Xn-1) + 
согласно принципу оптимальности для любого Sn-2 решение нужно выбирать так, чтобы оно вместе с оптимальным управлением на последнем n-ом шаге приводило бы к максимуму целевой функции на двух последних шагах. Следовательно, нужно найти максимум выражения (2) по всем допустимым управлениям Xn-1. Максимум этой суммы зависит от Sn-2, обозначается

Соотношение управления Xn-1 на (n-1) – шаге обозначается 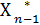
| <Хn-1>Хn> |
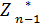

Следует обратить внимание на то, что выражение в фигурных скобках зависит только от Sn-2 и Xn-1, т.к. Sn-1 можно найти из уравнения состояний при k=n-1
В результате максимизации по переменной Xn-1 согласно уравнению (3) вновь получаем две функции:
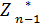
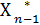
Далее рассматривается трех шаговая задача: к двум последним шагам присоединяется (n-2) шаг и т.д. Выражение (3) можно обобщить следующим образом.
Обозначим через 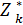
1. n-k+1 = n-n+1+1=2 – тогда 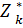
2. k=n-2 n-n+2+1 = 3 – на трех последних шагах
3. k=1 n-1+1 = n — на n последних шагах.
Итак по аналогии: для любых состояний Sk-1, произвольном управлении Хk и оптимальном уравнении на последующих (n-k) – шагах значение целевой функции на последних (n-k+1) – шагах равно
fk (Sk-1, Xk) + 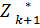
Максимум этой суммы зависит от Sk-1 и обозначается 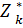
| <Хk>Хn> |
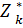
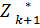
управление Xk на k-ом шаге, при котором достигается максимум (**)
| <Хn> |

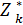

Управление Xk на k-ом шаге, при котором достигается максимум (4), обозначается 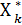
Уравнения (4) называются рекуррентными соотношениями Беллмана. Эти соотношения позволяют найти предыдущее значение функции, зная последующее. Если из (1) найти 
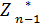
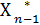
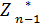
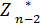
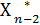
Процесс решения уравнений (1) и (4) называется условной оптимизацией.
В результате условной оптимизации получаются две последовательности

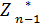
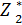
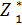
При этом набор значений для разных возможных значений Sn-1
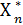
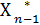

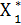
Используя эти последовательности, можно найти решение задачи динамического программирования при данных n и S0. По определению 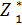
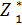
Далее следует последовательность условных оптимальных управлений и уравнений состояний.
При фиксированном S0 получаем 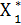
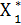
Далее из уравнений состояний находим 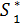
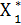
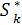
В последовательность условных оптимальных управлений


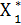
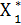

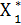


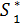
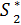
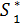

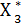
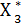
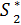

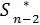
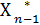
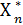
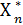

означает уравнения состояния, а => — последовательность условных оптимальных управлений.
В результате получаем оптимальное решение задачи динамического программирования:
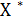


📹 Видео
Динамическое программированиеСкачать

МатЭк 8О-406б Динамическое программирование, метод Беллмана СеминарСкачать

Методы оптимизацииСкачать

Динамическое программирование (новый курс) лекция 2 часть 3 (постановка задачи)Скачать

динамическое программирование лекция 7Скачать

Экономика доступным языком: Номинальный и реальный ВВПСкачать

Алгоритмы (базовый поток) 10. Алгоритм Дейкстры, Форда-БеллманаСкачать

ЗАДАЧА ОБ ОПТИМАЛЬНОЙ ОСТАНОВКЕ (Елена Парилина) | ИПУ РАНСкачать

Оптимизационное моделирование: пример задачи нелинейного программированияСкачать

Динамическое программированиеСкачать

Графы: Алгоритм Форда БеллманаСкачать

Задача о замене оборудованияСкачать

Рентабельность активов и инвестицийСкачать


























