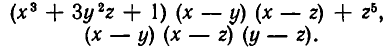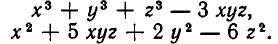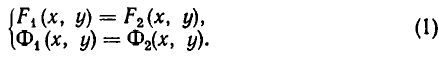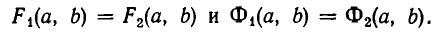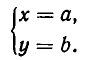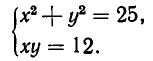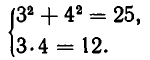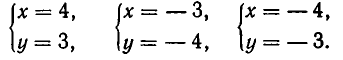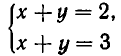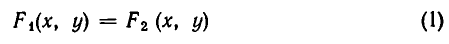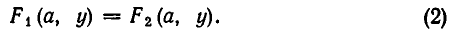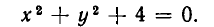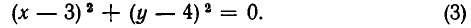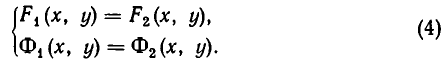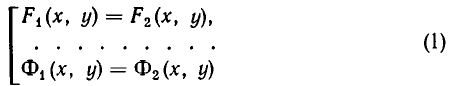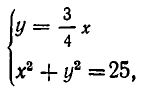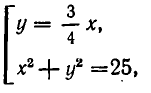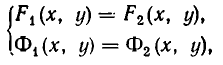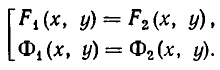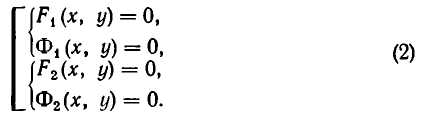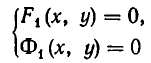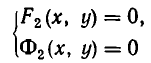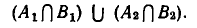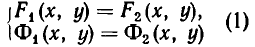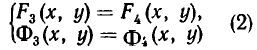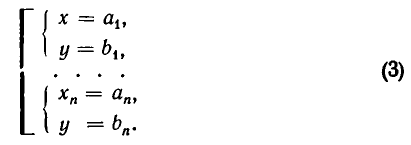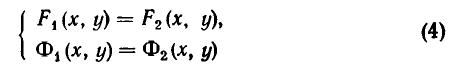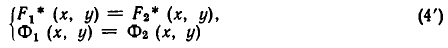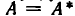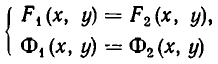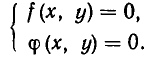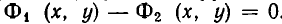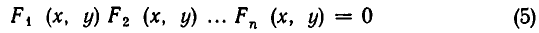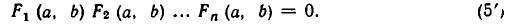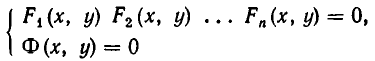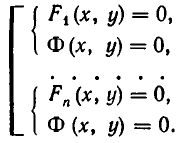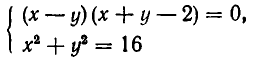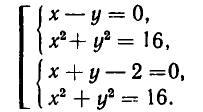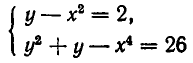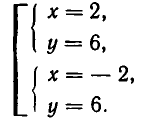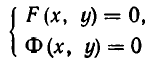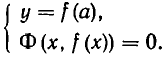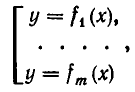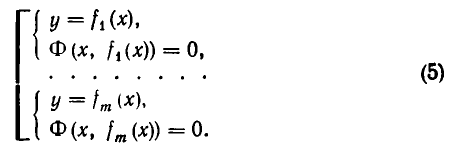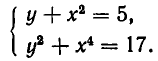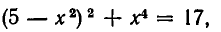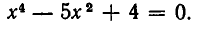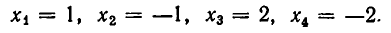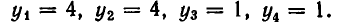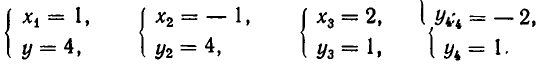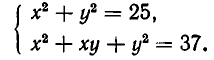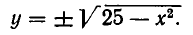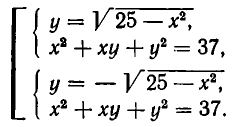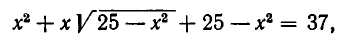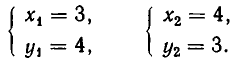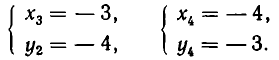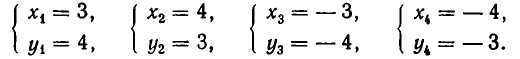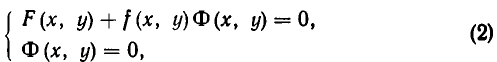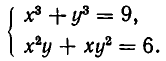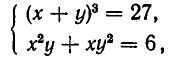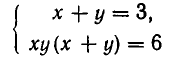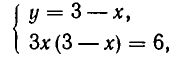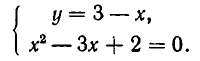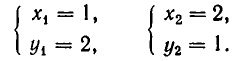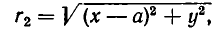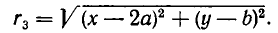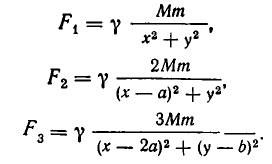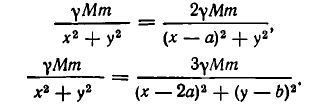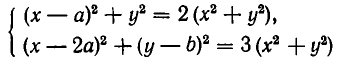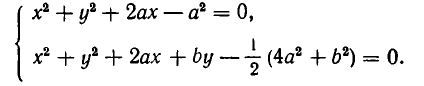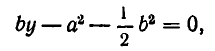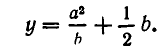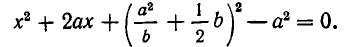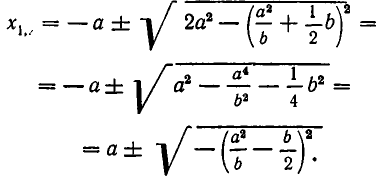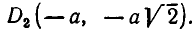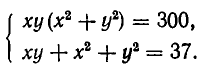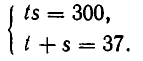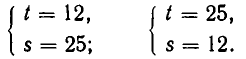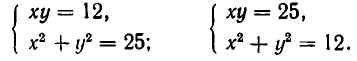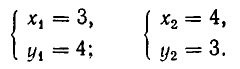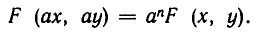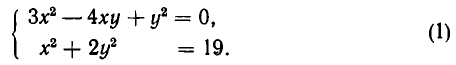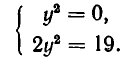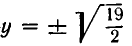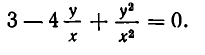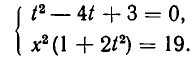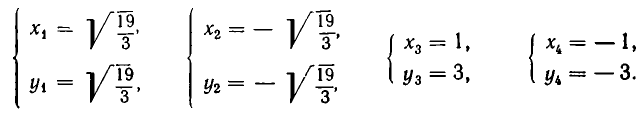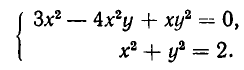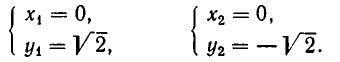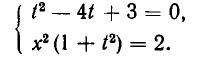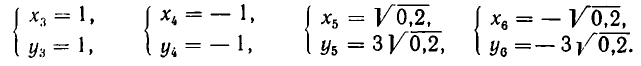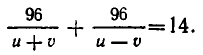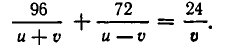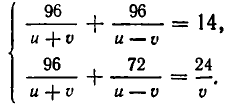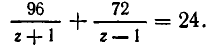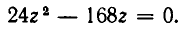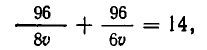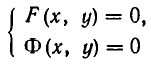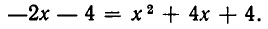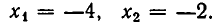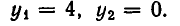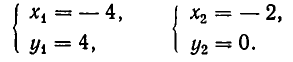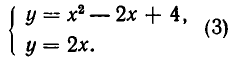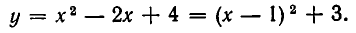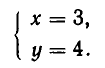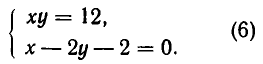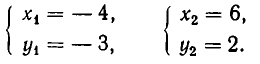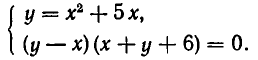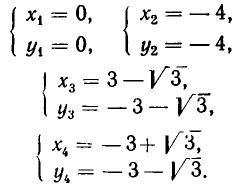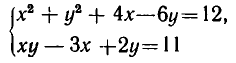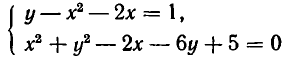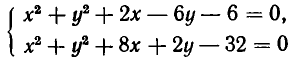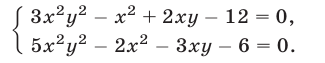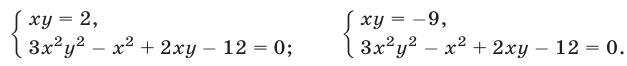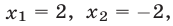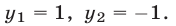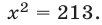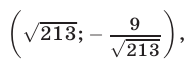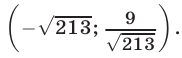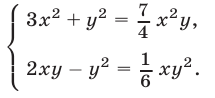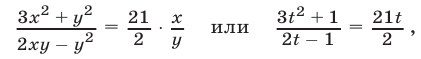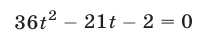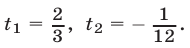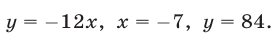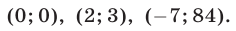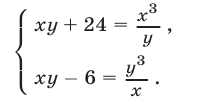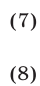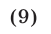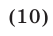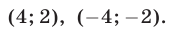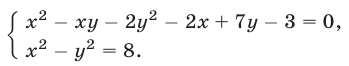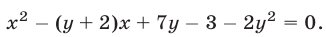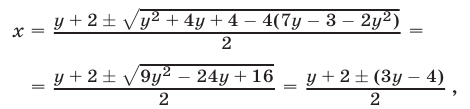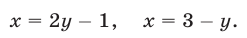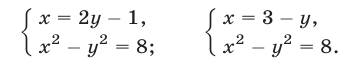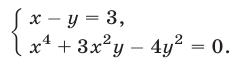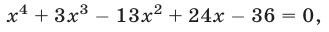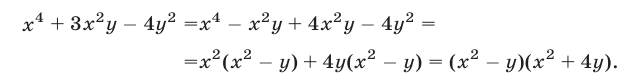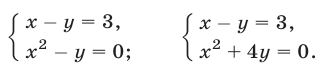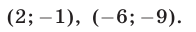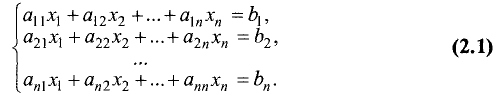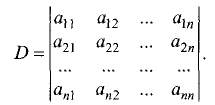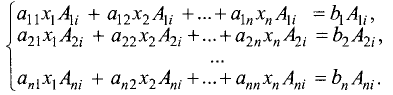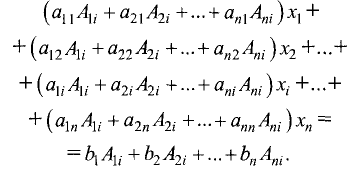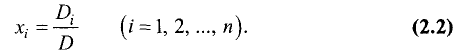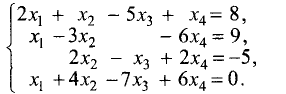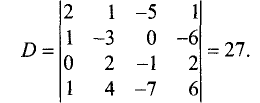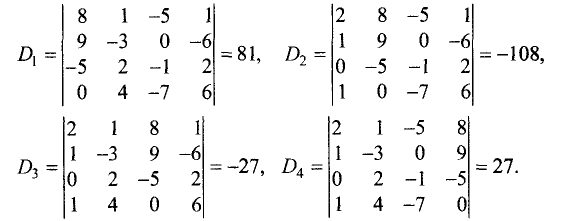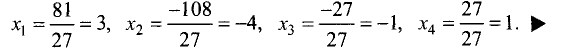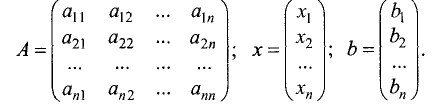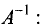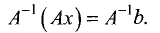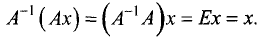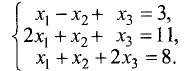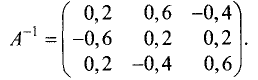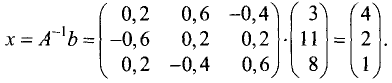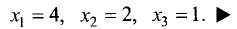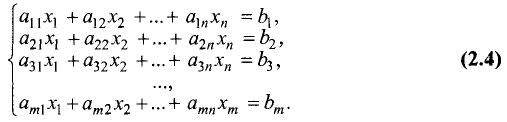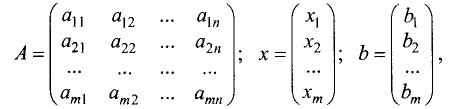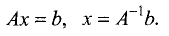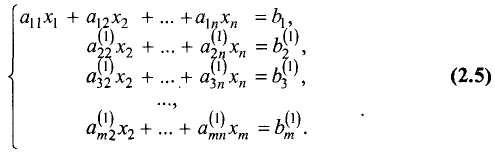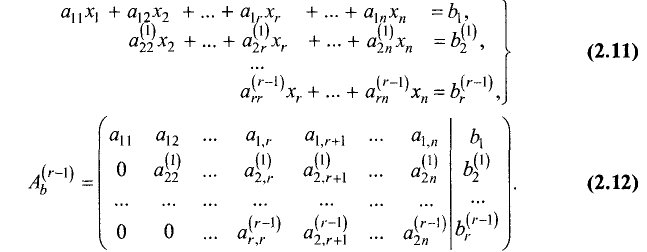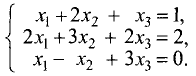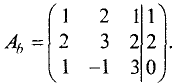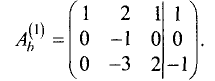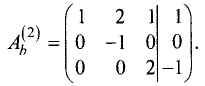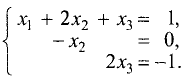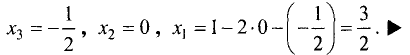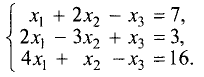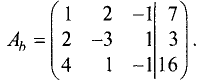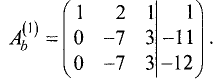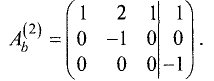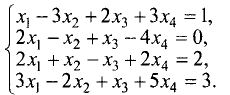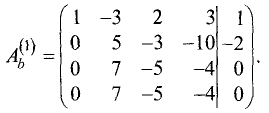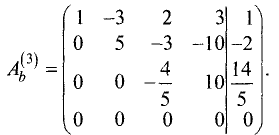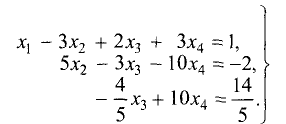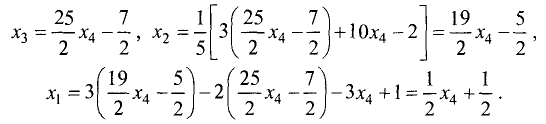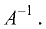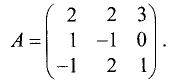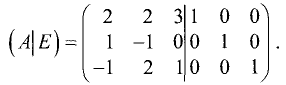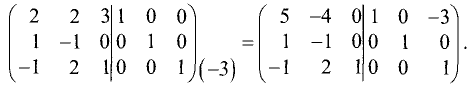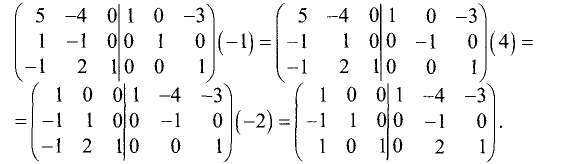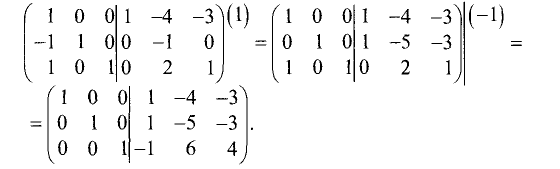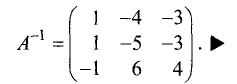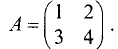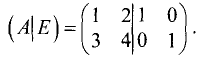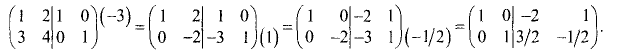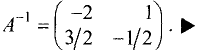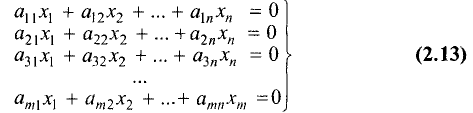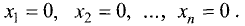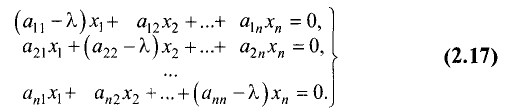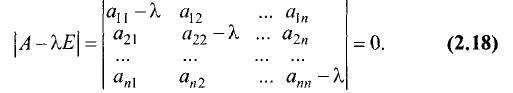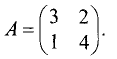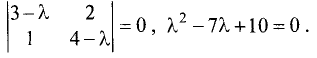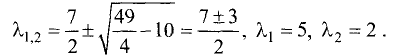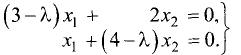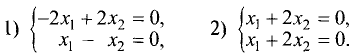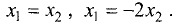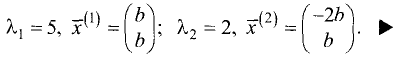Напомним, что уравнения с abvmh пеоеменными вида
описывают на координатной плоскости Оху прямую. Решение системы двух уравнений такого вида, как точки на координатной плоскости, должно принадлежать одновременно двум прямым, соответствующим уравнениям этой системы. Отсюда возможны следующие варианты:
- 1) прямые пересекаются, и система имеет единственное решение;
- 2) прямые параллельны, и система не имеет решения (несовместна);
- 3) прямые совпадают, т.с. ранг системы равен единице, и система имеет бесчисленное множество решений.
Уравнение с тремя переменными вида
описывает плоскость в трехмерном пространстве. Решение системы трех уравнений с тремя неизвестными — это точки пространства, которые должны принадлежать одновременно трем плоскостям, которые описываются уравнениями системы. В таком случае возможны следующие варианты:
- 1) три плоскости пересекаются в одной точке, и система имеет единственное решение;
- 2) три плоскости пересекаются по одной прямой — система имеет бесчисленное множество решений (все точки на этой прямой);
- 3) две плоскости совпадают, а третья пересекает их — бесчисленное множество решений (все точки прямой на пересечении трех плоскостей), ранг системы равен двум;
- 4) все три плоскости совпадают — все точки общей плоскости являются решениями, ранг системы равен единице;
- 5) хотя бы одна из плоскостей параллельна какой-либо из двух других — система несовместна;
- 6) плоскости пересекаются попарно по параллельным прямым — система несовместна.
В последних двух случаях несовместность системы уравнений обусловлена тем, что нет таких точек трехмерного пространства, которые принадлежали бы одновременно всем трем плоскостям.
В случае системы уравнений с п неизвестными каждое уравнение вида
можно интерпретировать как гиперплоскость в координатном пространстве А п Решение системы (4.1) — это такое множество точек пространства А», которые принадлежат одновременно всем т гиперплоскостям, соответствующим уравнениям этой системы.
- Урок математики в 9 классе по теме «Геометрическая интерпретация системы двух уравнений с двумя переменными»
- Системы алгебраических уравнений в математике с примерами решения и образцами выполнения
- Системы уравнений
- Геометрический смысл решений уравнений и систем уравнений с двумя неизвестными
- Совокупность уравнений
- Равносильные системы уравнений
- Метод подстановки
- Метод алгебраического сложения уравнений
- Метод введения новых неизвестных
- Системы однородных уравнений
- Геометрическая интерпретация решения систем двух уравнений с двумя неизвестными
- Решение других типов систем алгебраических систем уравнений
- Решение системы алгебраических уравнений по правилу Крамера и методом обратной матрицы
- Общий вид системы линейных алгебраических уравнений
- Решение системы линейных алгебраических уравнений методом Гаусса
- Вычисление обратной матрицы методом Гаусса
- Система линейных однородных уравнений
- Геометрическая интерпретация решения систем линейных уравнений.
- 📽️ Видео
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Урок математики в 9 классе по теме «Геометрическая интерпретация системы двух уравнений с двумя переменными»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 2 500 дидактических материалов для школьного и домашнего обучения
Столичный центр образовательных технологий г. Москва
Получите квалификацию учитель математики за 2 месяца
от 3 170 руб. 1900 руб.
Количество часов 300 ч. / 600 ч.
Успеть записаться со скидкой
Форма обучения дистанционная
Видеолекции для
профессионалов
- Свидетельства для портфолио
- Вечный доступ за 120 рублей
- 311 видеолекции для каждого
Урок математики в 9 классе по теме «Геометрическая интерпретация системы двух уравнений с двумя переменными».
18.02.2020 года учитель математики Бахир С.А.
Тип урока: изучение и первичное закрепление новых знаний
v создать условия для закрепления знаний по теме «Системы линейных уравнений с двумя переменными и способы их решения»;
v способствовать получению новых знаний, необходимых при моделировании реальных ситуаций с помощью систем уравнений и знакомству с геометрической интерпретацией систем двух уравнений с двумя переменными; развитию познавательной активности и самостоятельности учащихся;
v создать условия для формирования математической грамотности и культуры мышления.
Применяемые технологии : технология проблемного обучения, технология развития критического мышления.
Организационные формы работы с учащимися:
Оборудование: учебник, тетради, таблицы, схемы графиков, доска.
I. Организационный момент
II. Актуализация знаний
Шринивасана Рамануджан: «Для меня уравнение не имеет никакого смысла, если не выражает мысль Бога».
Ребята, как вы, наверное, уже догадались из этих слов индийского мыслителя, сегодня на уроке мы продолжим с вами работу над уравнениями, а именно над их системами. Вспомним основные методы решения уравнений и познакомимся с новым графическим методом решения систем двух уравнений с двумя переменными.
Учащимся предлагаются таблицы, которые необходимо заполнить по ходу урока. На начальном этапе заполняется графа «З», в которую учащиеся вписывают уже имеющиеся у них знания по теме урока. Например:
Что значит решить систему уравнений;
Способы решения систем уравнений:
способ подстановки и способ сложения;
Алгоритм решения систем двух линейных и нелинейных уравнений с двумя переменными.
III. Проверка домашнего задания:
Решить систему уравнений:
а) способом сложения
б) способом подстановки
IV . Изучение нового материала и первичное закрепление знаний
Решим систему уравнений 
Для этого построим в одной системе координат графики каждого из уравнений системы. Первое уравнение системы равносильно уравнению у = 
Графиком второго уравнения системы 
Обратите внимание на доску. Здесь мы видим два изображения (рис.3 и рис.4), на которых изображены графики конкретных функций, соответствующих определенным системам уравнений с двумя переменными. Давайте попробуем решить эти системы. (Самостоятельная работа учащихся с последующим объяснением алгоритма решения у доски).
Укажите с помощью изображенных графиков системы уравнений:
1) имеющие два решения,
2) имеющие одно решение,
3) не имеющие решений.
VI .Моделирование реальных процессов с использованием систем уравнений с двумя переменными.
Системы уравнений с двумя переменными помогают нам в моделировании реальных процессов. Обратимся вновь к учебнику и разберем задачу № 2 на с. 162. Из поселка А в поселок В вышел пешеход. Одновременно с ним из поселка В в поселок А выехал велосипедист. Через 50 минут они встретились. Сколько времени потребовалось бы пешеходу для того, чтобы пройти весь путь из А в В, если известно, что велосипедист проделал бы тот же путь на 4 часа быстрее пешехода?
Для решения задачи составим таблицу зависимостей между величинами.
Видео:Тема: Системы линейных уравнений. Урок: Системы линейных уравнений. Геометрическая интерпретацияСкачать

Системы алгебраических уравнений в математике с примерами решения и образцами выполнения
Целые рациональные функции от нескольких переменных: В этой главе мы изучим системы уравнений от нескольких переменных. В основном мы будем рассматривать системы алгебраических уравнений, то есть уравнений, обе части которых являются целыми рациональными функциями от неизвестных. Понятие целой рациональной функции от нескольких переменных определяется точно так же, как и в случае одного переменного; исходным, как и тогда, будет служить понятие целого рационального выражения.
Алгебраическое выражение, получающееся из чисел и букв x, у, … , z с помощью операций сложения и умножения, называется целым рациональным выражением от х, у, …, z. Примерами целых рациональных выражений являются:
Как и в случае выражений от одного переменного, каждое целое рациональное выражение от нескольких переменных можно привести к каноническому виду. Речь идет о суммах одночленов, то есть о выражениях вида 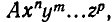
Правила действия над многочленами вытекают из основных законов алгебры.
Видео:Урок СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСССкачать

Системы уравнений
Рассмотрим некоторые общие вопросы теории систем уравнений. Для простоты ограничимся системами уравнений с двумя неизвестными, хотя основные результаты применимы и к системам уравнений с большим числом неизвестных.
Рассмотрим систему уравнений
Она выражает следующую задачу: найти все пары чисел (а, b) такие, что
Пары чисел (а, b), обладающие этим свойством, называют решениями системы (1). Если множество решений системы пусто, то система называется несовместной.
Тот факт, что пара (а, Ь) является решением системы уравнений с неизвестными х и у, записывается обычно в виде:
Например, пара чисел 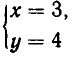
Помимо решения 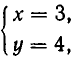
Позже мы увидим, что иных решений она не имеет.
Геометрический смысл решений уравнений и систем уравнений с двумя неизвестными
Возьмем любое уравнение относительно х и у:
и рассмотрим все точки М (х, у) некоторой плоскости, координаты которых удовлетворяют этому уравнению. Эти точки образуют не которое множество Г, и мы будем говорить, что уравнение (1) задает (или выражает) это множество. Обычно множество Г является некоторой линией. В этом случае уравнение (1) называют уравнением линии Г.
Чтобы найти точки линии 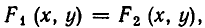
Может случиться, что это уравнение не имеет ни одного действительного корня. Тогда на линии нет точек с абсциссой х = а. Если же уравнение (2) имеет один или несколько корней, то каждому корню соответствует точка линии, имеющая абсциссу а.
Для некоторых уравнений на плоскости нет ни одной точки, координаты которых удовлетворяли бы этим уравнениям. Примером может служить
Ведь если х и у — действительные числа, то 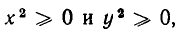
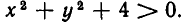
Так как 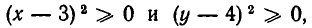
Однако такие случаи являются в некотором смысле исключи тельными, и мы ограничимся рассмотрением случаев, когда уравнение 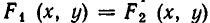
Перейдем теперь к выяснению геометрического смысла решений систем уравнений с двумя неизвестными. Возьмем такую систему:
Каждому из этих уравнений соответствует линия, координаты всех точек которой (и только этих точек!) удовлетворяют этому уравнению. Мы же ищем точки М (.х, у), координаты которых удовлетворяют обоим уравнениям. Ясно, что эти точки принадлежат обеим линиям, то есть являются точками их пересечения.
Итак, задача о решении системы уравнений равносильна зада че об отыскании точек пересечения соответствующих линий. Каждой точке пересечения линий соответствует решение системы.
Совокупность уравнений
образуют совокупность, если требуется найти все пары чисел х = а, у = b, удовлетворяющие хотя бы одному из уравнений (1). Все такие пары чисел (а, Ь) будем называть решениями совокупности (1). Геометрически решения совокупности (1) изображаются фигурой, образованной объединением всех кривых
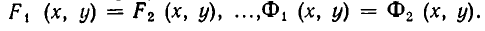
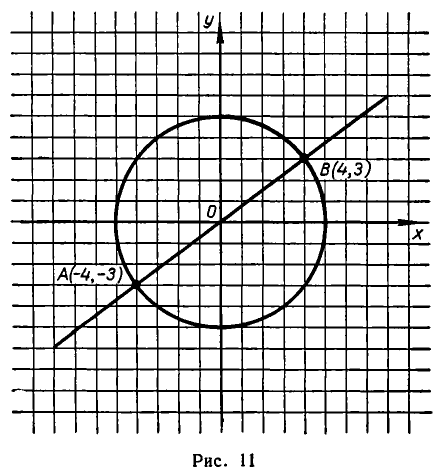
Например, возьмем уравнения 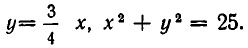
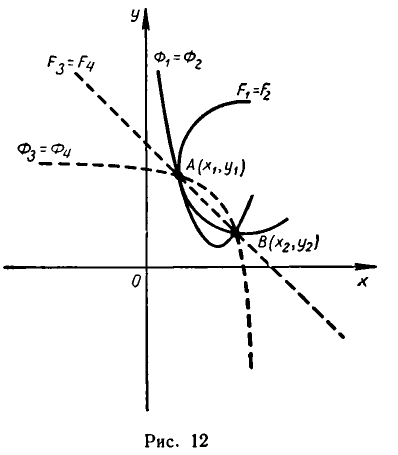
то решения будут изображаться точками пересечения прямой и окружности (то есть точками Л и В на рис. 11). Если же рассматривать эти уравнения как совокупность уравнений
то решение этой совокупности изображаются геометрической фигурой, получаемой объединением прямой и окружности.
Чтобы различать системы уравнений и совокупности уравнений, мы и стали обозначать систему уравнений так:
а совокупность уравнений так:
Можно говорить и о таком более сложном понятии, как совокупность систем уравнений. Например, возьмем такую запись:
Она означает, что надо найти решения системы уравнений
и найти решения системы уравнений
и объединить найденные решения.
Геометрически это изображается так: надо найти точки пересечения линий 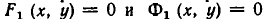
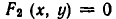
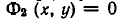
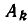
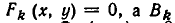
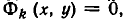
Равносильные системы уравнений
Две системы уравнений
называются равносильными, если всякое решение первой системы является решением второй, а всякое решение второй системы является решением первой.
В частности, любые две несовместные системы уравнений равносильны.
Геометрически это означает следующее: линии 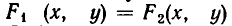
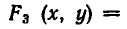
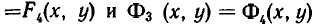
Процесс решения системы уравнений заключается в том, что ее последовательно заменяют равносильными ей системами уравнений (или совокупностями систем уравнений) до тех пор, пока не придут к совокупности вида:
Эта совокупность и дает решения заданной системы уравнений.
При решении систем уравнений чаще всего используются следующие теоремы о равносильности.
Теорема:
заменить любое из уравнений равносильным ему уравнением, то получим систему, равносильную первоначальной.
Доказательство:
Пусть 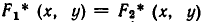
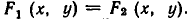
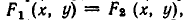
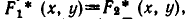
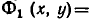
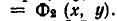
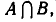
является пересечение 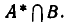
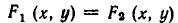
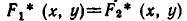
а значит, и 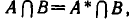
Из этой теоремы вытекает такое
Следствие:
Каждая система уравнений
равносильна некоторой системе уравнений вида
В самом деле, уравнение 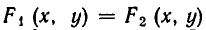
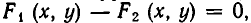
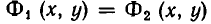
Теорема:
Если функции 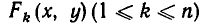
равносильно совокупности уравнений
Доказательство:
Если 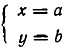
Но произведение нескольких чисел может равняться нулю тогда и только тогда, когда равен нулю хотя бы один из сомножителей. Поэтому для некоторого 
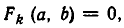
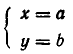
Обратно, если 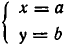
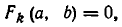
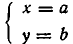
Из теоремы 2 вытекает.
Следствие:
равносильна совокупности систем уравнений
Например, система уравнений
равносильна совокупности систем
Это следствие позволяет сводить системы к совокупностям более простых систем
Метод подстановки
Теоремы п. 5 относятся по сути дела к отдельным уравнениям, а не к системе в целом. При решении систем уравнений применяются также преобразования уравнений, затрагивающие не одно уравнение, а несколько. Например, для решения системы
мы находим из первого уравнения выражение у через 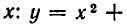
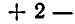
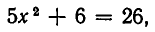
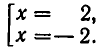
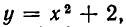
Метод, которым была решена эта система, называется методом подстановки. Он позволяет сводить решение системы уравнений с двумя неизвестными к более простой задаче — решению одного уравнения с одним неизвестным. Выясним теперь, на чем же основан метод подстановки. Для этого докажем следующую теорему.
Теорема:
равносильна системе уравнений
Доказательство:
Пусть 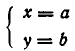
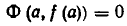
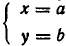
Обратно, пусть 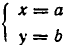
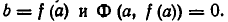
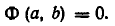
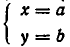
Тем самым равносильность систем уравнений (1) и (2) доказана.
Из теорем 2 и 3 вытекает
Следствие:
Если уравнение F (х, у)=0 равносильно уравнению 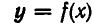
равносильна системе уравнений
Мы уже говорили, что теорема 3 лежит в основе метода решения систем уравнений с двумя неизвестными, называемого методом исключения неизвестных. Он состоит в следующем.
Пусть задана система уравнений
Выразим из первого уравнения системы у через х, то есть заменим уравнение F(х, у)= 0 равносильным ему уравнением у = f(х). Полученное выражение для у подставим во второе уравнение, то есть заменим систему уравнений (1) равносильной ей системой
Уравнение Ф (х,f(x)) является уже уравнением с одним неизвестным. Решая его, получим корни 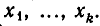

Часто приходится заменять уравнение F(х,у)= 0 не одним уравнением вида у = f(х), а совокупностью
таких уравнений. Тогда и система (1) заменяется совокупностью систем
Из каждой системы этой совокупности получаем описанным выше методом решения заданной системы, после чего объединяем их.
Примеры:
- Решить систему уравнений:
Из первого уравнения системы находим 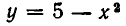
или, после упрощения,
Корнями этого биквадратного уравнения являются числа:
Им соответствуют значения:
Значит, решения заданной системы уравнений имеют вид:
2. Решить систему уравнений:
Из первого уравнения системы получаем:
Значит, нам надо решить совокупность двух систем уравнений:
Делая в первой системе подстановку, получаем:
или 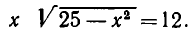
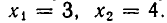
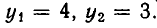
Точно так же доказывается, что вторая система имеет решения:
Следовательно, заданная система имеет решения:
Метод алгебраического сложения уравнений
Кроме метода подстановки, при решении систем алгебраических уравнений применяется метод алгебраического сложения. Он основан на следующей теореме.
Теорема:
Если к одному из уравнений системы
прибавить другое уравнение, умноженное на любой множитель f(x, y), определенный при всех допустимых значениях неизвестных, а второе уравнение оставим неизменным, то получится система уравнений, равносильная исходной.
Таким образом, система (1) равносильна системе
где множитель f(х,у) определен при всех допустимых значениях неизвестных.
Доказательство:
Пусть х = а, у = b — решение системы (1), то есть F(а, b)=0 и Ф(а, b)= 0.
Умножим обе части равенства Ф(а, b)=0 на число f(а, b) и прибавим к равенству F (а, b)= 0. Мы получим, что F(а, b)+(а, b) Ф(а,b)= 0, а потому х =а, у = b удовлетворяет и системе (2).
Точно так же доказывается, что любое решение системы уравнений (2) удовлетворяет системе уравнений (1). Значит, системы уравнений (1) и (2) равносильны.
Из теоремы 4 вытекает такое
Следствие:
Если к одному из уравнений системы (1) прибавить другое уравнение системы, умноженное на любое число, а второе уравнение оставить неизменным, то получим систему, равносильную первоначальной.
Покажем, как применяются эти утверждения для решения систем уравнений. Пусть дана система уравнений:
Здесь нецелесообразно выражать х через у или у через х, так как мы получили бы довольно сложное иррациональное уравнение. Поэтому поступим иначе. Прибавим к первому уравнению системы второе уравнение, умноженное на 3. В силу формулы для куба суммы получим систему уравнений:
равносильную заданной. Эта система равносильна системе:
(поскольку уравнение 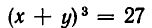
А теперь выразим из первого уравнения у через х и подставим во второе уравнение. Мы получим:
Из второго уравнения находим: 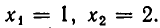
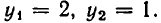
Задача:
Массы трех планет 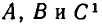
система координат. Координаты планет равны соответственно A(0,0), В (а, 0), С (2а, b). При каком значении b на плоскости существует точка, в которой притяжение ко всем трем планетам одинаково?
Решение:
По закону всемирного тяготения сила притяжения между телами с массами 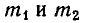
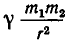
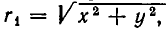
а до точки С (b, с) равно
Поэтому силы, с которыми тело массы m, находящееся в точке D, притягивается к планетам, равны
По условию задачи должны выполняться условия 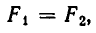
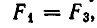
После сокращения обоих уравнений на 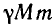
Вычтем первое уравнение из второго. Мы получим, что
Подставляя это значение у в первое уравнение, получаем для х квадратное уравнение
Из него находим:
Отсюда получаем, что х принимает действительные значения лишь в случае, когда 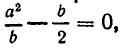
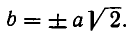
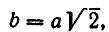
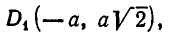
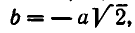
Метод введения новых неизвестных
Для решения многих систем оказывается удобно ввести вместо х и у новые неизвестные. Рассмотрим следующий пример:
Если положить 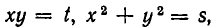
Решая эту систему, получаем, что
Так как 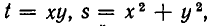
Решениями первой системы являются:
Вторая же система не имеет действительных решений.
Общего правила для выбора новых неизвестных не существует. Однако в некоторых случаях можно указать полезные правила.
Системы однородных уравнений
Назовем f (х, у) однородным многочленом относительно х и у степени n, если при замене х на ах и у на ау F (х, у) умножается на
Например, 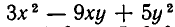
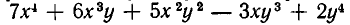
Пусть одно из уравнений системы имеет вид: F (х,у) = 0, где F (х, у)— однородный многочлен. Тогда решение системы сводится к решению двух уравнений, каждое из которых содержит лишь одно неизвестное. Покажем на примере, как это делается.
Пусть дана система уравнений:
Посмотрим сначала, есть ли у этого уравнения решения, для которых х =0. Подставляя х = 0 в оба уравнения системы, получаем систему уравнений:
Эта система несовместна, так как из первого уравнения получаем у = 0, а из второго —
Итак, система не имеет решений, для которых х = 0. Поэтому первое уравнение системы можно разделить на 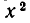
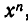
Положим у — tх. Мы придем к системе уравнений:
Корнями первого уравнения являются 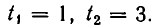
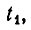
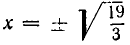
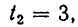
В следующем примере система имеет решения, для которых х = 0:
При х = 0 первое уравнение обращается в равенство 0=0, а второе принимает вид 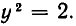
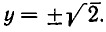
Другие решения получаются так же, как и в первом случае. Мы делим первое уравнение системы на 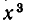
Из первого уравнения находим 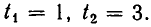
Задача:
От пристани А одновременно отправились вниз по течению катер и плот. Катер спустился вниз по течению на 96 км, затем повернул обратно и вернулся в А через 14 часов. Найти скорость катера в стоячей воде, если известно, что катер встретил плот на обратном пути на расстоянии 24 км от А.
Решение:
Сначала составим систему уравнений. В качестве неизвестных выберем скорость u катера в стоячей воде и скорость течения v. Тогда скорость катера при движении по течению равна u+v, а при движении против течения u-v. Значит, чтобы пройти вниз по течению 96 км, ему надо 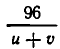
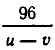
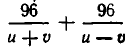
Чтобы получить второе уравнение, найдем, какое время затратил катер до встречи с плотом. Он прошел 96 км вниз по течению и 72 км против течения. На это он затратил 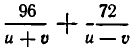
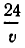
Мы получим систему уравнений:
При замене u на ut и v на vt обе части второго уравнения умножаются на 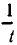
Освобождаясь от знаменателей, получим:
Так как 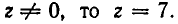
откуда v = 2 (км/ч). Поэтому u = 14 км/ч.
Геометрическая интерпретация решения систем двух уравнений с двумя неизвестными
Мы уже знаем, что решение системы двух уравнений с двумя неизвестными
геометрически истолковывается как отыскание точек пересечения двух линий. Этим можно воспользоваться для приближенного решения системы уравнений. Именно, если изобразить линии F(х, у) = 0 и Ф(х, у) = 0, мы сможем найти координаты точек пересечения этих линий и тем самым значения неизвестных. Поскольку линии чертятся лишь приближенно, мы получаем не точные, а приближенные значения решений системы. Тем не менее, решая графически систему, мы можем узнать, сколько она имеет решений, и, хотя бы грубо, найти приближенные значения этих решений.
При графическом решении систем уравнений мы сталкиваемся с различными кривыми. В курсе геометрии были выведены уравнения прямой, окружности, параболы, гиперболы и эллипса. В дальнейшем мы будем пользоваться этими кривыми.
Рассмотрим некоторые примеры систем уравнений.
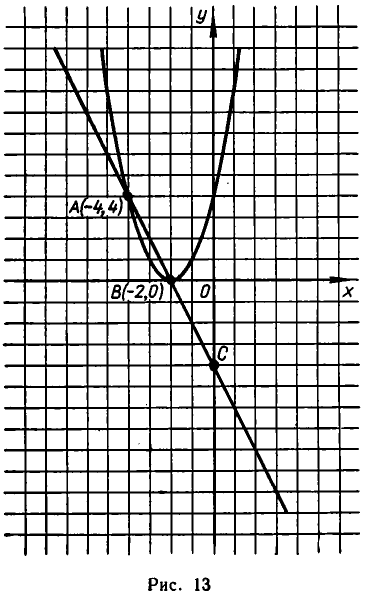
Пусть дана система
Выразив из уравнения (2) у через х и подставив в первое уравнение, получаем квадратное уравнение:
Подставив их во второе уравнение, получаем:
Итак, система имеет два решения:
Построим теперь линии, выражаемые уравнениями (1) и (2). Уравнение (1) — это уравнение параболы 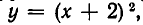
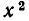
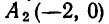
Парабола может иметь с прямой линией не две, а одну точку пересечения и даже не иметь ни одной точки пересечения.
Возьмем систему уравнений:
Ее единственное решение:
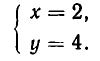
Из рис. 14 мы видим, что прямая у = 2х касается параболы
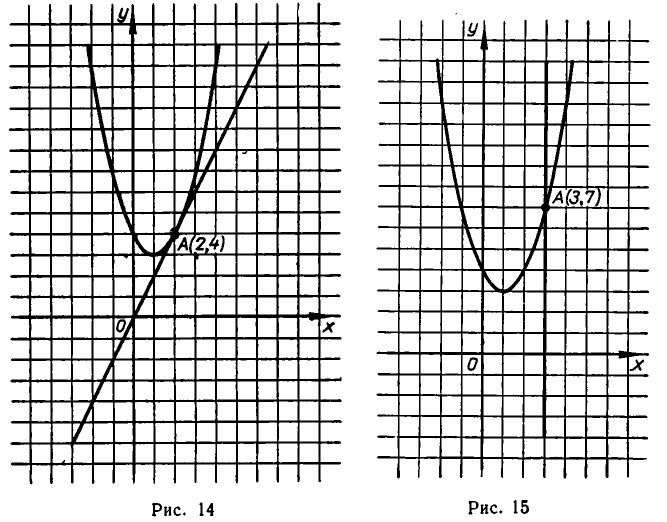
тоже имеет одно решение:
Но в этом случае прямая не касается параболы, а пересекает ее (см. рис. 15).
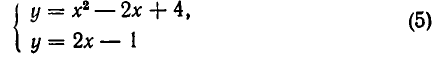
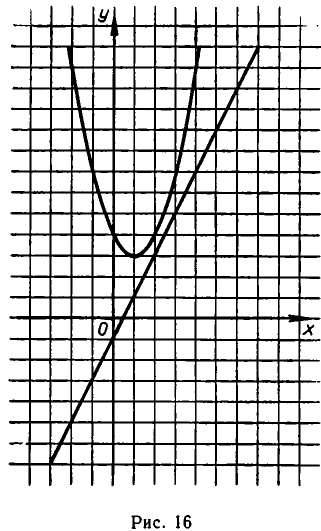
не имеет ни одного решения — здесь прямая и парабола не пересекаются (см. рис. 16).
Теперь рассмотрим систему, геометрический смысл которой заключается в отыскании точек пересечения прямой и гиперболы. Пусть система имеет вид:
Решая ее способом подстановки, находим решения:
Эти же решения получаются графическим способом (см. рис. 17). Однако следует иметь в виду, что графический способ дает лишь приближенные значения корней и, решая систему (6) графически, мы не можем быть уверены, что решение имеет вид х = —4, у = —3, а не, например, х = —4,01, у = —2,99.
Как и в случае параболы, может случиться, что прямая имеет не две, а меньше общих точек с гиперболой.
Перейдем к системам, в которых оба уравнения имеют вторую степень. Можно доказать, что такие системы уравнений имеют не более четырех решений.
Вообще можно доказать, что система двух уравнений с двумя неизвестными такая, что первое уравнение имеет степень m, а второе — степень n, имеет не более mn решений.
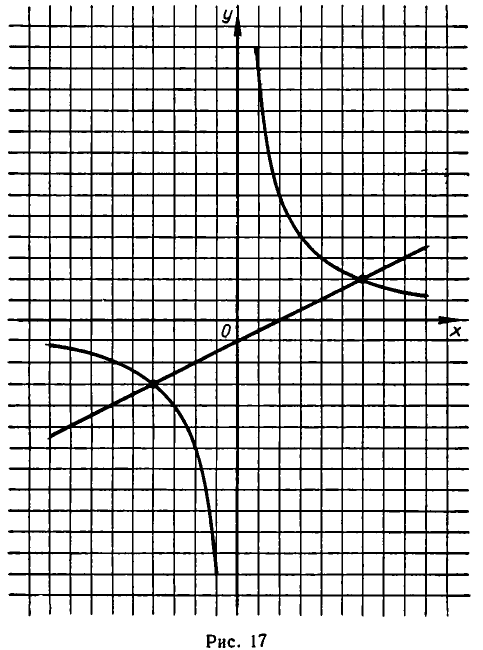
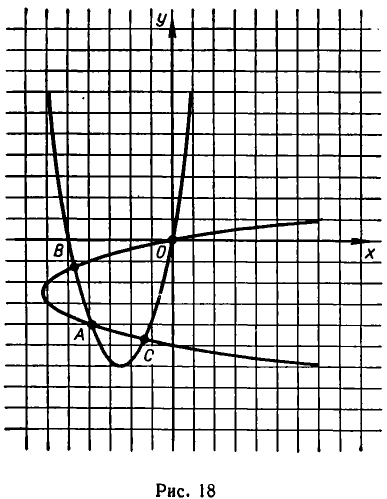
Рассмотрим, например, систему:
Первое из этих уравнений представляет параболу с осью, параллельной оси ординат, а второе — параболу с осью, параллельной оси абсцисс (см. рис. 18). Из рисунка видно, что эти параболы пересекаются в четырех точках. Чтобы найти координаты точек пересечения,
решим эту систему методом алгебраического сложения. Именно, вычтем из уравнения (8) уравнение (7). Мы получим равносильную систему уравнений:
Эта система равносильна совокупности систем:
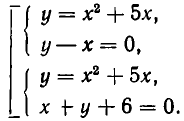
Обе системы этой совокупности решаются методом подстановки. Мы получаем при этом следующие решения заданной системы:
тоже имеет четыре решения. Она выражает задачу об отыскании точек пересечения окружности и гиперболы (см. рис. 19). Что бы решить эту систему, надо прибавить к первому уравнению удвоенное второе уравнение.
В некоторых случаях получается меньше чем четыре решения системы. Например, система
имеет два решения. Она выражает задачу об отыскании точек пересечения параболы и окружности (рис. 20).
Столько же решений имеет система
(пересечение двух окружностей) (рис. 21).
Видео:7 класс, 37 урок, Системы двух линейных уравнения с двумя переменными. Основные понятияСкачать

Решение других типов систем алгебраических систем уравнений
Пример:
Решить систему уравнений
Решение:
Из данной системы можно исключить 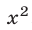
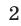
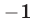
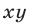
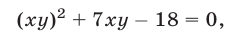
откуда 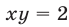
Система (1), (2), равносильная системе (1), (3), распадается на две системы:
Из первой системы находим
Из второй системы получаем
Ответ. 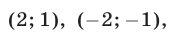
Пример:
Решить систему уравнений
Решение:
Если 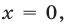
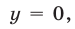
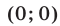
Пусть 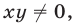
где 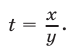
имеет корни
Заметим, что при 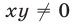
Если 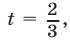
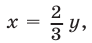
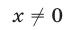
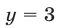
Если 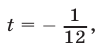
Ответ.
Пример:
Решить систему уравнений
Решение:
Допустимые значения 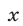
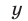
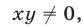
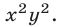
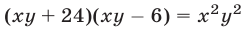
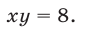
Так как обе части уравнений (7) и (8) отличны от нуля, то система (9), (7) равносильна системе (7), (8). Исключая у из системы (9), (7), получаем
Из (10) следует, что 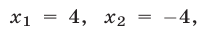
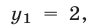
Ответ.
Пример:
Решить систему уравнений
Решение:
Запишем первое уравнение в виде
Решив это уравнение как квадратное относительно 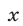
Таким образом, исходная система распадается на следующие две системы:
Пример:
Решить систему уравнений
Решение:
Исключив 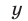
нахождение корней которого — совсем не простая задача. Более эффективный способ основан на разложении левой части уравнения (12) на множители:
Отсюда вытекает, что система (11), (12) распадается на следующие две системы:
Первая из этих систем не имеет действительных решений, а вторая имеет два решения.
Ответ.
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
Видео:Решение системы неравенств с двумя переменными. 9 класс.Скачать

Решение системы алгебраических уравнений по правилу Крамера и методом обратной матрицы
Пусть дана система линейных уравнений, состоящая из n
линейных уравнений с n неизвестными:
Здесь 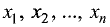
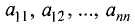
циенты при неизвестных, 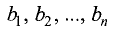
Определитель, состоящий из коэффициентов при неизвестных,
называется определителем системы.
Для рассматриваемого случая определитель системы имеет вид
Предположим, что этот определитель отличен от нуля. Пусть i —
любое число от 1 до n . Умножим обе части первого равенства
системы уравнений (2.1) на алгебраическое дополнение 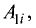
получающееся вычеркиванием первой строки и i-го столбца в определителе системы. Обе части второго равенства этой системы умножим на алгебраическое дополнение 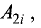
Сложим левые и правые части получившейся системы
уравнений, скомпоновав их следующим образом:
Коэффициентом при 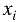
системы D. При всех остальных х коэффициенты будут равны нулю,
так как они являются суммой произведений всех элементов столбцов
определителя на алгебраические дополнения соответствующих
элементов другого столбца (п. 5 свойств определителей, § 1.9). Правая
часть равенства является определителем, полученным из
определителя системы D после замены в нем i-го столбца столбцом из
свободных членов системы уравнений. Обозначим этот определитель 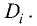
Так как 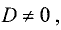
Этот метод решения системы линейных уравнений называется
правилом Крамера.
Правило Крамера. Пусть D — определитель системы п линейных
уравнений, состоящий из коэффициентов при неизвестных, a 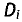
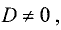
Пример:
Решить систему линейных уравнений:
Решение:
Определитель этой системы отличен от нуля:
После замены в этом определителе соответствующих столбцов
столбцом свободных членов получим
Решение системы уравнений:
Решить систему линейных уравнений можно, используя матричный метод. Для этих целей коэффициенты данной системы, неизвестные и свободные члены представим в виде матриц:
Тогда система линейньк уравнений в матричной форме имеет вид
Умножим слева эту матрицу на
Преобразуем левую часть равенства:
Таким образом, решение в матричной форме можно записать в виде
Пример:
Решить систему линейных уравнений:
Решение:
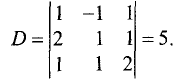
Определитель данной системы
Обратную матрицу находим по схеме, приведенной в § 1.11:
Находим матрицу решений:
Таким образом, система имеет следующее решение:
Видео:Решение систем уравнений второго порядка. 8 класс.Скачать

Общий вид системы линейных алгебраических уравнений
Систему из m линейных уравнений с n неизвестными, или систему m х n, можно записать в общем виде следующим образом:
Если так же, как и в предыдущем разделе, ввести обозначения
то система линейных уравнений в матричной форме и ее решение
примут вид
Решение системы линейных алгебраических уравнений методом Гаусса
Метод Гаусса состоит в последовательном исключении переменных. При этом на первом шаге из второго уравнения исключается 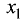
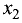
Шаг 1. Предположим, что коэффициент при 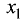
уравнении системы (2.4) 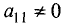
уравнений местами добьемся того, что 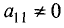
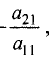
Умножим первое уравнение на 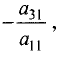
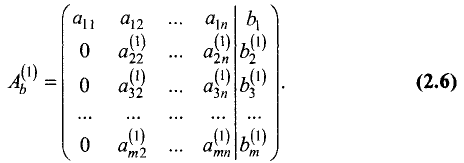
Для удобства записи обычно используют расширенную матрицу системы, отделяя в ней вертикальной чертой столбец свободных членов. После первого шага данная матрица принимает вид:
Шаг 2. Предположим, что коэффициент при 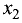
уравнении системы (2.5) 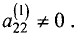
уравнений местами добьемся того, что 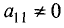
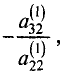
третьим уравнением системы (2.5) или матрицы (2.6) и результат
запишем в виде третьего уравнения системы (2.7) или матрицы
(2.8). Аналогично поступаем с остальными уравнениями системы:
Продолжая процесс последовательного исключения переменных, после (r-1)-го шага получим систему уравнений и расширенную матрицу:
Последние m-r уравнений в системе (2.9) для совместной
системы (2.4) являются тождествами: 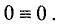
чисел 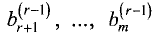
расширенная матрица (2.10) принимают вид
После отбрасывания уравнений, являющихся тождествами,
число оставшихся уравнений может быть либо равно числу
переменных r=n, либо меньше числа переменных. В первом случае
матрица имеет треугольный вид, а во втором — ступенчатый. Переход от системы уравнений (2.4) к равносильной ей системе (2.11)
называется прямым ходом метода Гаусса, а нахождение переменных из системы (2.11) — обратным ходом.
Пример:
Методом Гаусса решить систему уравнений
Решение:
Расширенная матрица этой системы имеет вид
Шаг 1. Расширенную матрицу первого шага получаем за счет
умножения первой строки на —2 и сложения результата со второй
строкой, а также за счет умножения первой строки на -1 и сложения
результата с третьей строкой:
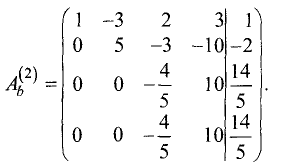
Ш а г 2. Расширенную матрицу первого шага получаем за счет
умножения второй строки на -3 и сложения результата с третьей строкой:
Эта матрица имеет треугольную форму и соответствует системе
линейных уравнений
Отсюда последовательно находим
Пример:
Методом Гаусса решить систему уравнений
Решение:
Расширенная матрица этой системы имеет вид
Ш а г 1. Расширенную матрицу первого шага получаем за счет
умножения первой строки на —2 и сложения результата со второй
строкой, а также за счет умножения первой строки на -4 и сложения результата с третьей строкой:
Ш а г 2. Расширенную матрицу первого шага получаем за счет
умножения второй строки на —1 и сложения результата с третьей строкой:
Уравнение,соответствующее третьей строке последней матрицы, противоречиво. Оно имеет вид 0 = -1. Следовательно, данная система несовместна. ►
Пример:
Методом Гаусса решить систему уравнений
Решение:
Расширенная матрица этой системы имеет вид
Ш а г 1. Первую строку последовательно умножаем на числа -2; —2;
-3 и складываем результат с соответствующими строками исходной
расширенной матрицы:
Ш а г 2. Умножаем вторую строку на 
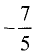
Шаг 3. Умножаем третью строку на -1.
После удаления последнего уравнения приведенная система
уравнений принимает вид
Из этой системы обратным ходом метода Гаусса находим
Так как 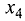
система имеет бесконечное множество решений. ►
Вычисление обратной матрицы методом Гаусса
Этот наиболее простой метод вычисления обратной матрицы
состоит в следующем. Пусть А — невырожденная матрица.
Припишем к ней справа единичную матрицу Е. Далее с помощью
элементарных преобразований над строками расширенной матрицы 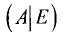
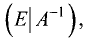
Пример:
Найти матрицу, обратную исходной:
Решение:
Составим расширенную матрицу:
Приведем левую половину этой матрицы к единичной матрице:
Последний столбец левой половины матрицы принял вид
последнего столбца единичной матрицы:
Последний и предпоследний столбцы левой половины матрицы
приняли вид последнего и предпоследнего столбцов единичной матрицы:
Правая половина этой расширенной матрицы является искомой
обратной матрицей, т.е.
Пример:
Найти матрицу, обратную исходной:
Решение:
Составим расширенную матрицу:
Приведем левую половину этой матрицы к единичной матрице:
Правая половина этой расширенной матрицы является искомой
обратной матрицей, т.е.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Система линейных однородных уравнений
Система m линейных уравнений с n переменными называется системой линейных однородных уравнений, если все ее свободные члены равны нулю.
Такая система имеет вид
Система линейных однородных уравнений всегда совместна, так
как она имеет, по крайней мере, нулевое (тривиальное) решение
Если система (2.13) имеет n линейных уравнений, а ее определитель отличен от нуля, то такая система имеет только нулевое решение. Это следует из правила Крамера. Ненулевое решение возможно для систем линейных однородных уравнений, у которых определитель равен нулю или m Собственные значения и собственные векторы матриц
Пусть матрица имеет порядок n или, что то же самое, размер n х n.
Вектор 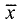
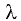
Число 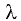
соответствующим вектору 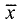
Перенеся правую часть (2.15) в левую и принимая во внимание
соотношение 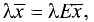
Уравнение (2.16) эквивалентно системе линейных однородных
уравнений
Для существования ненулевого решения системы линейных
однородных уравнений (2.17) необходимо и достаточно, чтобы
определитель коэффициентов этой системы равнялся нулю, т.е.
Этот определитель является многочленом n-й степени относительно
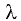
уравнение (2.18) — характеристическим уравнением матрицы А. Корни характеристического уравнения соответствуют собственным числам матрицы А. Определив набор этих чисел, для каждого из них можно найти собственный вектор.
Пример:
Найти собственные числа и собственные векторы
матрицы
Решение:
Характеристическое уравнение этой матрицы имеет вид
Корни характеристического уравнения
Для двух переменных система уравнений (2.17), эквивалентная
уравнению (2.15) собственного вектора, представляется в виде
Подставив сюда значения корней 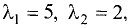
системы уравнений:
Каждая система является одним уравнением, что и следовало
ожидать. Это связано с тем, что определитель системы равен нулю.
Из первой системы для 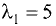
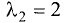
координаты собственных векторов связаны соотношениями
Поскольку 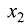
значению матрицы соответствует бесконечное множество собственных векторов различной длины. Положим 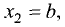
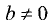
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Геометрическая интерпретация решения систем линейных уравнений.
Мы уже упоминали ранее, что прямая на плоскости описывается уравнением первой степени с двумя переменными:
Решению систем из уравнений такого вида в главе 1 мы уделили особое внимание. Добавим только, что система из двух уравнений такого вида означает, что ее решение, как и точки на координатной плоскости, должны принадлежать одновременно двум прямым, соответствующим уравнениям этой системы.
Отсюда возможны следующие варианты: а) прямые пересекаются, и тогда система имеет единственное решение; б) прямые параллельны, и система не имеет решений (несовместна); в) прямые совпадают, т.е. ранг системы равен единице, и система имеет бесчисленное множество решений.
Итак, вернемся к уравнению (2.9), в котором коэффициенты А и В не равны одновременно нулю, т.е.
1. Пусть В Ф 0. Тогда уравнение (2.9) можно записать в виде
Обозначим к = -AIВ, b = -CIB. Если А Ф 0, С Ф 0, то получим у = кх + b (уравнение прямой с угловым коэффициентом); если А Ф 0, С = 0, то у = кх (уравнение прямой, проходящей через начало координат); если А = 0, С Ф 0, то у = b (уравнение прямой, параллельной оси Оу); если А = 0, С = 0, то у = 0 (уравнение оси Ох).
2. Пусть В = 0, А Ф 0. Тогда уравнение (2.9) примет вид х =—.
Обозначим а = -С/А. Если С Ф 0, то получим х-а (уравнение прямой, параллельной оси Оу); если С = 0, то х = 0 (уравнение оси Оу).
Таким образом, при любых значениях коэффициентов А, В (не равных одновременно нулю) и С уравнение (2.9) есть уравнение некоторой прямой линии на плоскости Оху. Можно показать, что уравнение любой прямой на плоскости можно получить из (2.9) при некоторых значениях А, В, С.
Поэтому уравнение (2.9) называется общим уравнением прямой. Заметим, что в отличие от уравнения пучка прямых (2.5) общее уравнение (2.9) включает и уравнение любой вертикальной прямой, параллельной оси Оу.
📽️ Видео
ГРАФИК ЛИНЕЙНОГО УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСС видеоурокСкачать

Линейное уравнение с двумя переменными. 7 класс.Скачать

Нелинейные уравнения с двумя переменными и их геометрический смысл. 9 класс.Скачать

7 класс, 8 урок, Линейное уравнение с двумя переменными и его графикСкачать

Системы уравнений с двумя переменными. Алгебра 9 классСкачать

Решение систем уравнений второй степени. Алгебра, 9 классСкачать

Решение системы линейных уравнений графическим способом. 7 классСкачать

Системы нелинейных уравнений с двумя переменными. Способ подстановки. Алгебра 9 классСкачать

Графический способ решения систем уравнений. Алгебра, 9 классСкачать

ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать

Урок: Геометрическая интерпретация решения системы трёх линейных уравнений. Вырожденный случайСкачать

Решение систем уравнений методом подстановкиСкачать