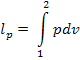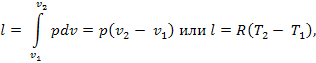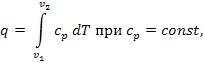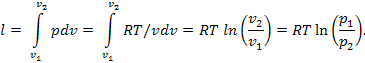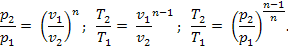Какому термодинамическому процессу соответствует уравнение v2 v1 t2 t1 (2 видео)

Содержание

Основы теплотехники
Термодинамические процессы
Изохорный процесс
Изобарный процесс
Изотермический процесс
Адиабатный процесс
Политропный процесс
Блог об энергетике
энергетика простыми словами
Основные термодинамические процессы
Изохорный процесс
Изобарный процесс
Изотермический процесс
Адиабатный процесс
Политропный процесс
Какому термодинамическому процессу соответствует уравнение v2 v1 t2 t1
🔍 Видео

Видео:Физика 10 класс (Урок№24 - Первый закон термодинамики.)Скачать

Основы теплотехники

Видео:Обратимые и необратимые процессы. Энтропия. Второй закон термодинамики. 10 класс.Скачать

Термодинамические процессы

Как упоминалось в предыдущей статье, термодинамическим процессом называют изменение состояния системы, в результате которого хотя бы один из ее параметров (температура, объем или давление) изменяет свое значение. Впрочем, если учесть, что все параметры термодинамической системы неразрывно взаимосвязаны, то изменение любого из них неизбежно влечет изменение хотя бы одного (в идеале) или нескольких (в реальности) параметров. В общем случае можно сказать, что термодинамический процесс связан с нарушением равновесия системы, и если система находится в равновесном состоянии, то никаких термодинамических процессов в ней протекать не может.

Равновесное состояние системы — понятие абстрактное, поскольку невозможно изолировать что-либо материальное от окружающего мира, поэтому в любой реальной системе неизбежно протекают разнообразные термодинамические процессы. При этом в некоторых системах могут иметь место настолько медленные, почти незаметные изменения, что связанные с ними процессы можно условно считать состоящими из последовательности равновесных состояний системы. Такие процессы называют равновесными или квазистатическими .
Еще один возможный сценарий последовательных изменений в системе, после которых она возвращается к исходному состоянию, называют круговым процессом или циклом . Понятия равновесного и кругового процесса лежат в основе многих теоретических выводов и прикладных приемов термодинамики.

Изучение термодинамического процесса заключается в определении работы, совершенной в данном процессе, изменения внутренней энергии, количества теплоты, а также в установлении связи между отдельными величинами, характеризующими состояние газа.

Из всех возможных термодинамических процессов наибольший интерес представляют изохорный , изобарный , изотермический , адиабатный и политропный процессы.

Изохорный процесс

Изохорным называют термодинамический процесс, протекающий при постоянном объеме. Такой процесс может совершаться при нагревании газа, помещенного в закрытый сосуд. Газ в результате подвода теплоты нагревается, и его давление возрастает.
Изменение параметров газа в изохорном процессе описывает закон Шарля: p₁/T₁ = p₂/T₂ , или в общем случае:

Давление газа на стенки сосуда прямо пропорционально абсолютной температуре газа.

Так как в изохорном процессе изменение объема dV равно нулю, то можно сделать вывод, что вся подведенная к газу теплота расходуется на изменение внутренней энергии газа (никакая работа не совершается) .

Изобарный процесс

Изобарным называют термодинамический процесс, протекающий при постоянном давлении. Такой процесс можно осуществить, поместив газ в плотный цилиндр с подвижным поршнем, на который действует постоянная внешняя сила при отводе и подводе теплоты.
При изменении температуры газа поршень перемещается в ту или иную сторону; при этом объем газа изменяется в соответствии с законом Гей-Люссака:

Это означает, что в изобарном процессе объем занимаемый газом, прямо пропорционален температуре.
Можно сделать вывод, что изменение температуры в этом процессе неизбежно приведет к изменению внутренней энергии газа, а изменение объема связано с выполнением работы, т. е. при изобарном процессе часть тепловой энергии тратится на изменение внутренней энергии газа, а другая часть – на выполнение газом работы по преодолению действия внешних сил. При этом соотношение между затратами теплоты на увеличение внутренней энергии и на выполнение работы зависит от теплоемкости газа.

Изотермический процесс

Изотермическим называют термодинамический процесс, протекающий при неизменной температуре.
Практически осуществить изотермический процесс с газом очень трудно. Ведь необходимо соблюсти условие, чтобы в процессе сжатия или расширения газ успевал обмениваться температурой с окружающей средой, поддерживая собственную температуру постоянной.
Изотермический процесс описывается законом Бойля-Мариотта: pV = const , т. е. при постоянной температуре величина давления газа обратно пропорциональна его объему.

Очевидно, что при изотермическом процессе внутренняя энергия газа не изменяется, поскольку его температура постоянна.
Чтобы выполнялось условие постоянства температуры газа, от него необходимо отводить теплоту, эквивалентную работе, затраченной на сжатие:

Используя уравнение состояния газа, проделав ряд преобразований и подстановок, можно сделать вывод, что работа газа при изотермическом процессе определяется выражением:

Адиабатный процесс

Адиабатным называют термодинамический процесс, протекающий без теплообмена рабочего тела с окружающей средой. Подобно изотермическому, осуществить на практике адиабатный процесс очень сложно. Такой процесс может протекать с рабочим телом, помещенным в сосуд, например, цилиндр с поршнем, окруженный высококачественным теплоизолирующим материалом.
Но какой бы качественный теплоизолятор мы не применяли в данном случае, некоторым, пусть даже ничтожно малым, количеством теплоты рабочее тело и окружающая среда неизбежно будут обмениваться.
Поэтому на практике можно создать лишь приближенную модель адиабатного процесса. Тем не менее, многие термодинамические процессы, осуществляемые в теплотехнике, протекают настолько быстро, что рабочее тело и среда не успевают обмениваться теплотой, поэтому с некоторой степенью погрешности такие процессы можно рассматривать как адиабатные.

Для вывода уравнения, связывающего давление и объем 1 кг газа в адиабатном процессе, запишем уравнение первого закона термодинамики:

Поскольку для адиабатного процесса теплопередача dq равна нулю, а изменение внутренней энергии есть функция теплопроводности от температуры: du = c_vdT , то можно записать:

Продифференцировав уравнение Клапейрона pv = RT , получим:

Выразим отсюда dT и подставим в уравнение (3) . После перегруппировки и преобразований получим:

С учетом уравнения Майера R = c_p – c_v последнее выражение можно переписать в виде:

Разделив полученное выражение на c_v и обозначив отношение c_p/c_v буквой k , после интегрирования уравнения (4) получим (при k = const) :

ln vk + ln p = const или ln pvk = const или pvk = const .

Полученное уравнение является уравнением адиабатного процесса, в котором k – показатель адиабаты.
Если предположить, что объемная теплоемкость c_v является величиной постоянной, т. е. c_v = const , то работу адиабатного процесса можно представить в виде формулы (приводится без вывода) :

Политропный процесс

В отличие от рассмотренных выше термодинамических процессов, когда какой-либо из параметров газа оставался неизменным, политропный процесс характеризуется возможностью изменения любого из основных параметров газа. Все рассмотренные выше термодинамические процессы являются частными случаями политропных процессов.
Общее уравнение политропного процесса имеет вид pv n = const , где n – показатель политропы — постоянная для данного процесса величина, которая может принимать значения от — ∞ до + ∞ .

Очевидно, что придавая показателю политропы определенные значения, можно получить тот или иной термодинамический процесс – изохорный, изобарный, изотермический или адиабатный.
Так, если принять n = 0 , получим p = const – изобарный процесс, если принять n = 1 , получим изотермический процесс, описываемый зависимостью pv = const ; при n = k процесс является адиабатным, а при n равном — ∞ или + ∞ . мы получим изохорный процесс.

Так как уравнение политропы по своему содержанию аналогично уравнению адиабатного процесса, то формулы, устанавливающие связь между параметрами политропного процесса будут аналогичны таковым для адиабатного процесса с той лишь разницей, что показатель адиабаты k нужно заменить на показатель политропы n .
Тогда:

Работа газа при политропном процессе может быть определена по формуле:

Теплоемкость при политропном процессе (приводится без вывода) :

Скачать теоретические вопросы к экзаменационным билетам
по учебной дисциплине «Основы гидравлики и теплотехники»
(в формате Word, размер файла 68 кБ)

Скачать рабочую программу
по учебной дисциплине «Основы гидравлики и теплотехники» (в формате Word):

Скачать календарно-тематический план
по учебной дисциплине «Основы гидравлики и теплотехники» (в формате Word):

Видео:Решение задач на термохимические уравнения. 8 класс.Скачать

Блог об энергетике

Видео:Применение первого закона термодинамики к изопроцессам. 10 класс.Скачать

энергетика простыми словами

Видео:Решение графических задач на тему Газовые законыСкачать

Основные термодинамические процессы

Основными процессами в термодинамике являются:

изохорный, протекающий при постоянном объеме;
изобарный, протекающий при постоянном давлении;
изотермический, происходящий при постоянной температуре;
адиабатный, при котором теплообмен с окружающей средой отсутствует;
политропный, удовлетворяющий уравнению pv n = const.

Изохорный, изобарный, изотермический и адиабатный процессы являются частными случаями политропного процесса.

При исследовании термодинамических процессов определяют:

уравнение процесса в p—v иT—s координатах;
связь между параметрами состояния газа;
изменение внутренней энергии;
величину внешней работы;
количество подведенной теплоты на осуществление процесса или количество отведенной теплоты.

Изохорный процесс

При изохорном процессе выполняется условие v = const.

Из уравнения состояния идеального газа (pv = RT) следует:

т. е. давление газа прямо пропорционально его абсолютной температуре:

Работа расширения в изохорном процессе равна нулю (l = 0), так как объем рабочего тела не меняется (Δv = const).

Количество теплоты, подведенной к рабочему телу в процессе 1-2 при c_v = const определяется по формуле:

Т. к.l = 0, то на основании первого закона термодинамики Δu = q, а значит изменение внутренней энергии можно определить по формуле:

Изменение энтропии в изохорном процессе определяется по формуле:

Изобарный процесс

Изобарным называется процесс, протекающий при постоянном давлении p = const. Из уравнения состояния идеального газа слуедует:

т. е. в изобарном процессе объем газа пропорционален его абсолютной температуре.

Работа будет равна:

Количество теплоты при c_p = const определяется по формуле:

Изменение энтропии будет равно:

Изотермический процесс

При изотермическом процессе температура рабочего тела остается постоянной T = const, следовательно:

т. е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении – снижается.

Работа процесса будет равна:

Так как температура остается неизменной, то и внутренняя энергия идеального газа в изотермическом процессе остается постоянной (Δu = 0) и вся подводимая к рабочему телу теплота полностью превращается в работу расширения:

При изотермическом сжатии от рабочего тела отводится теплота в количестве, равном затраченной на сжатие работе.

Изменение энтропии равно:

Адиабатный процесс

Адиабатным называется процесс изменения состояния газа, который происзодит без теплообмена с окружающей средой. Так как dq = 0, то уравнение первого закона термодинамики для адиабатного процесса будет иметь вид:

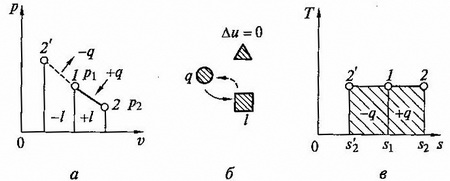
В адиабатном процессе работа расширения совершается только за счет расходования внутренней энергии газа, а при сжатии, происходящем за счет действия внешних сил, вся совершаемая ими работа идет на увеличение внутренней энергии газа.

Обозначим теплоемкость в адиабатном процессе через c_ад, и условие dq = 0 выразим следующим образом:

Это условие говорит о том, что теплоемкость в адиабатном процессе равна нулю (c_ад = 0).

и уравнение кривой адиабатного процесса (адиабаты) в p, v-диаграмме имеет вид:

В этом выражении k носит название показателя адиабаты (так же ее называют коэффициентом Пуассона).

k_{выхлопных газов ДВС} = 1,33

Из предыдущих формул следует:

Техническая работа адиабатного процесса (l_техн) равна разности энтальпий начала и конца процесса (i₁ – i₂).

Адиабатный процесс, происходящий без внутреннего трения в рабочем теле, называется изоэнтропийным. В T, s-диаграмме он изображается вертикальной линией.

Обычно реальные адиабатные процессы протекают при наличии внутреннего трения в рабочем теле, в результате чего всегда выделяется теплота, которая сообщается самому рабочему телу. В таком случае ds > 0, и процесс называется реальным адиабатным процессом.

Политропный процесс

Политропным называется процесс, который описывается уравнением:

Показатель политропы n может принимать любые значения в пределах от -∞ до +∞, но для данного процесса он является постоянной величиной.

Из уравнения политропного процесса и уравнения Клайперона можно получить выражение, устанавливающее связь между p, vи Tв любых двух точках на политропе:

Работа расширения газа в политропном процессе равна:

В случае идеального газа эту формулу можно преобразовать:

Количество подведенной или отведенной в процессе теплоты определяется с помощью первого закона термодинамики:

представляет собой теплоемкость идеального газа в политропном процессе.

При c_v, k и n = const c_n = const, поэтому политропный процесс иногда определят как процесс с постоянной теплоемкостью.

Политропный процесс имеет обобщающее значение, ибо охватывает всю совокупность основных термодинамических процессов.

Графическое представление политропа в p, v координатах в зависимости от показателя политропа n.

pv 0 = const (n = 0) – изобара;

pv = const (n = 1) – изотерма;

p 0 v = const, p 1/∞ v = const, pv ∞ = const – изохора;

n > 0 – гиперболические кривые,

n По материалам моего конспекта лекций по термодинамике и учебника «Основы энергетики». Автор Г. Ф. Быстрицкий. 2-е изд., испр. и доп. — М. :КНОРУС, 2011. — 352 с.

Видео:Первый закон термодинамики. 10 класс.Скачать

Какому термодинамическому процессу соответствует уравнение v2 v1 t2 t1

Характеристики основных видов термодинамических процессов идеальных газов при изменениях таких параметров, как температура, объем, давление и производимая газом работа.

Виды процессов. Основными процессами в технической термодинамике, весьма важными и в теоретическом, и в прикладном отношениях, являются:

изохорный – протекающий при постоянном объеме;

изобарный – протекающий при постоянном давлении;

изотермический – протекающий при постоянной температуре;

адиабатный – при котором отсутствует теплообмен с окружающей средой;

политропный – удовлетворяющий уравнению pv n = const.

Первые четыре процесса являются частными случаями политропного процесса.

При исследовании этих процессов определяют уравнение процесса в координатах p, v и T, s,связь между параметрами состояния газа, измерение внутренней энергии, величину внешней работы и количество отведенной теплоты.

Изохорный процесс. При изохорном процессе выполняется условие dv = 0 или v = const.Из уравнения идеального газа следует, что

т.е. давление газа прямо пропорционально его абсолютной температуре:

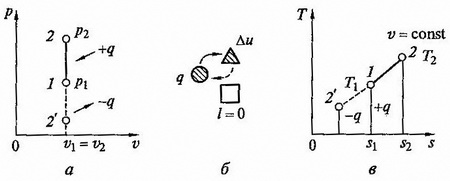
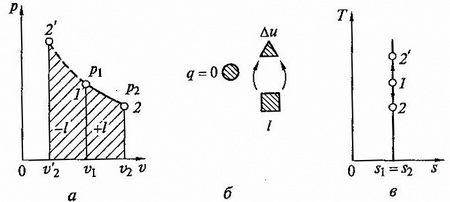
рис. 2.4 Изохорный процесс на p — v и T — s диаграммах (а, в) и схема энергобаланса (б)

Графики процесса на p – v и T – s – диаграммах, а также схема энергобаланса представлены на рисунке. Работа расширения в этом процессе равна нулю, так как dv = 0. Количество теплоты, подведенной к рабочему телу в процессе 1 – 2 при c_v = const, определяется из соотношения

Так как l = 0, то в соответствии с первым законом термодинамики

Изобарный процесс. Изобарным называется процесс, происходящий при постоянном давлении. Из уравнения состояния идеального газа при p = const находим

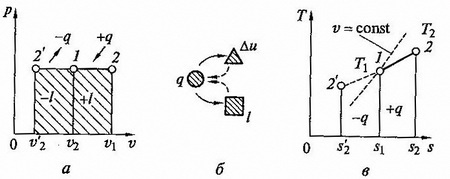
т.е. в изобарном процессе объем газа пропорционален его абсолютной температуре (закон Гей-Люссака). Графики процесса на p — v и T – s – диаграммах, а ттакже схема знергобалланса изображены на рис. 2.5.

рис.2.5. Изобарный процесс на p — v и T — s — диаграммах (а,в) и схема энергобаланса (б)

Количество теплоты сообщаемое газу при нагревании (или отдаваемое им при охлаждении), находим из уравнения

Изотермический процесс. При изотермическом процессе температура постоянная, следовательно, pv = RT = const или p₂/p₁ = v₁/v₂, т.е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении – падает (закон Бойля – Мариотта).

Графиком изотермического процесса в координатах p, v (рис.2.6,а) является равнобокая гипербола, для которой координатные оси служат асимптомами.

Так как энергия не меняется, то внутренняя энергия идеального газа в данном процессе остается постоянной (Δu = 0) и вся подводимая к газу теплота полностью превращается в работу расширения q = l.

рис. 2.6. Изотермический процесс на p — v и T — s — диаграммах (а,в) и схема энергобаланса (б)

При изотермическом сжатии от газа отводится теплота в количестве, равным затраченной на сжатие работе. Схема энергобаланса и и график изобарного процесса на T – s – диаграмме приведены на рис. 2.6, б,в.

Адиабатный процесс. Адиабатным называется процесс изменения состояния газа, который происходит без теплообмена с окружающей средой. Такой процесс соответствует случаю, когда сосуд или оболочка, вмещающие в себе газ, изолированы в тепловом отношении от окружающей среды. Для данного случая уравнение первого закона термодинамики, поскольку в нем по _{условию} _{dq = 0}_{, принимает вид}

Это означает, что в адиабатном процессе работа расширения совершается только за счет расходования внутренней энергии газа и что при сжатии, происходящем за счет действия внешних сил, вся совершаемая ими работа идет на увеличение внутренней энергии газа.

Обозначим теплоемкость в адиабатном процессе через с_ад и выразим условие du= 0 следующим образом:

Это условие говорит о том, что теплоемкость в адиабатном процессе равна нулю, т.е. с_ад = 0. Известно, что

Уравнение кривой адиабатного процесса (адиабаты) в координатах p, v (рис.2.7 а) имеет вид

где k – называется показателем адиабаты (эту величину называют также коэффициентом Пуассона).

т.е. техническая работа адиабатного процесса расширения равна разности энтальпий начала и конца процесса.

Рис.2.7 Адиабптный процесс на p — v и T — s lиаграммах (а, в) и схема энергобаланса (б)

Адиабатный процесс, происходящий без внутреннего трения в рабочем теле, называется изоэнтропийным. На T – s диаграмме (рис.2.7, в) он изображается вертикальной прямой.

Обычно реальные адиабатные процессы протекают при наличии внутреннего трения в рабочем теле, в результате которого всегда выделяется теплота, которая тут же сообщается самому рабочему телу. В этом случае ds > 0, процесс называется реальным адиабатным процессом.

Политропный процесс и его обобщающее значение. Политропным называется процесс, который происходит при постоянной теплоемкости и описывается уравнением

Показатель политропы n может принимать любое численное значение в пределах от -∞ до +∞, но для данного процесса он является величиной постоянной.

Из уравнения (2.13) и уравнения Клайперона нетрудно получить выражения, устанавливающие связь между p v и T в любых двух точках на политропе: