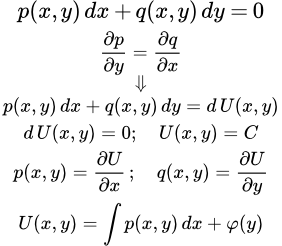Какое высказывание не отражает признак уравнения в полных дифференциалах тест

Видео:Дифференциальные уравнения, 6 урок, Уравнения в полных дифференциалахСкачать

Список вопросов теста

Вопрос 1

1. Вставить пропущенное слово

Дифференциальным уравнением (ДУ) называется уравнение, связывающее между собой независимую переменную x , искомую функции y и её … или дифференциалы.

Варианты ответов

• интеграл
• производные
• значения функции

Вопрос 2

ДУ первого порядка называется уравнение вида

Варианты ответов

• F(x,y,y’)=0
• F(x,y’,y» )=0
• aх+b=0

Вопрос 3

Варианты ответов

• линейное уравнение
• ДУ с разделяющими переменными
• ДУ второго порядка с постоянными коэффициентами

Вопрос 4

Характеристическое уравнение ДУ имеет вид

Варианты ответов

• а2х+с=0
• ( λ)^2+pλ+q=0
• ( λ)^2+pλ+q=с(х)

Вопрос 5

Общим решением дифференциального уравнения n-го порядка называется

Варианты ответов

• Решение, содержащее n независимых произвольных постоянных
• Решение, выраженное относительно независимой переменной
• Решение, полученное без интегрирования

Вопрос 6

Отношение двух однородных функций одинаковых степеней есть однородная функция

Варианты ответов

• Нулевой степени
• Первой степени
• Степени на одну ниже степеней исходных функций

Вопрос 7

Какое высказывание не отражает признак уравнения в полных дифференциалах?

Варианты ответов

• Левая часть уравнения представляет собой сумму частных дифференциалов
• Частная производная по одной переменной одного слагаемого и Частная производная по другой переменной другого слагаемого равны
• Выражение, зависящее от y, входит только в левую часть, а выражение, зависящее от x — только в правую часть

Вопрос 8

Решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами содержит тригонометрические функции, если

Варианты ответов

• Корни характеристического уравнения – комплексные
• Корни характеристического уравнения — действительные и различные
• Корни характеристического уравнения — вещественные и равные

Вопрос 9

При решении линейного дифференциального уравнения первого порядка не применяется

Варианты ответов

• Замена переменной
• Разделение переменных
• Метод неопределённых коэффициентов

Вопрос 10

Первым шагом решения уравнения является:

Видео:Уравнение в полных дифференциалахСкачать

Дифференциальные уравнения в полных дифференциалах

Видео:11. Уравнения в полных дифференциалахСкачать

Введение

Если найдена такая функция U ( x, y ) , то уравнение принимает вид:
dU ( x, y ) = 0 .
Его общий интеграл:
U ( x, y ) = C ,
где C – постоянная.

Если дифференциальное уравнение первого порядка записано через производную:
,
то его легко привести к форме (1). Для этого умножим уравнение на dx . Тогда . В результате получаем уравнение, выраженное через дифференциалы:
(1) .

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Свойство дифференциального уравнения в полных дифференциалах

Для того, чтобы уравнение (1) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось соотношение:
(2) .

Доказательство

Далее мы полагаем, что все функции, используемые в доказательстве, определены и имеют соответствующие производные в некоторой области значений переменных x и y . Точка x ₀ , y ₀ также принадлежит этой области.

Докажем необходимость условия (2).
Пусть левая часть уравнения (1) является дифференциалом некоторой функции U ( x, y ) :
.
Тогда
;
.
Поскольку вторая производная не зависит от порядка дифференцирования, то
;
.
Отсюда следует, что . Необходимость условия (2) доказана.

Докажем достаточность условия (2).
Пусть выполняется условие (2):
(2) .
Покажем, что можно найти такую функцию U ( x, y ) , что ее дифференциал:
.
Это означает, что существует такая функция U ( x, y ) , которая удовлетворяет уравнениям:
(3) ;
(4) .
Найдем такую функцию. Проинтегрируем уравнение (3) по x от x ₀ до x , считая что y – это постоянная:
;
;
(5) .
Дифференцируем по y считая, что x – это постоянная и применим (2):

.
Уравнение (4) будет выполнено, если
.
Интегрируем по y от y ₀ до y :
;
;
.
Подставляем в (5):
(6) .
Итак, мы нашли функцию, дифференциал которой
.
Достаточность доказана.

В формуле (6), U ( x ₀ , y ₀) является постоянной – значением функции U ( x, y ) в точке x ₀ , y ₀ . Ей можно присвоить любое значение.

Видео:Уравнение в полных дифференциалахСкачать

Как распознать дифференциальное уравнение в полных дифференциалах

Рассмотрим дифференциальное уравнение:
(1) .
Чтобы определить, является ли это уравнение в полных дифференциалах, нужно проверить выполнение условия (2):
(2) .
Если оно выполняется, то это уравнение в полных дифференциалах. Если нет – то это не уравнение в полных дифференциалах.

Пример

Проверить, является ли уравнение в полных дифференциалах:
.

Здесь
, .
Дифференцируем по y , считая x постоянной:

.
Дифференцируем по x , считая y постоянной:

.
Поскольку:
,
то заданное уравнение – в полных дифференциалах.

Видео:12. Интегрирующий множитель. Уравнения в полных дифференциалахСкачать

Методы решения дифференциальных уравнений в полных дифференциалах

Метод последовательного выделения дифференциала

Наиболее простым методом решения уравнения в полных дифференциалах является метод последовательного выделения дифференциала. Для этого мы применяем формулы дифференцирования, записанные в дифференциальной форме:
du ± dv = d ( u ± v ) ;
v du + u dv = d ( uv ) ;
;
.
В этих формулах u и v – произвольные выражения, составленные из любых комбинаций переменных.

Пример 1

Ранее мы нашли, что это уравнение – в полных дифференциалах. Преобразуем его:
(П1) .
Решаем уравнение, последовательно выделяя дифференциал.
;
;
;
;

.
Подставляем в (П1):
;
.

Метод последовательного интегрирования

В этом методе мы ищем функцию U ( x, y ) , удовлетворяющую уравнениям:
(3) ;
(4) .

Проинтегрируем уравнение (3) по x , считая y постоянной:
.
Здесь φ ( y ) – произвольная функция от y , которую нужно определить. Она является постоянной интегрирования. Подставляем в уравнение (4):
.
Отсюда:
.
Интегрируя, находим φ ( y ) и, тем самым, U ( x, y ) .

Пример 2

Решить уравнение в полных дифференциалах:
.

Ранее мы нашли, что это уравнение – в полных дифференциалах. Введем обозначения:
, .
Ищем Функцию U ( x, y ) , дифференциал которой является левой частью уравнения:
.
Тогда:
(3) ;
(4) .
Проинтегрируем уравнение (3) по x , считая y постоянной:
(П2)
.
Дифференцируем по y :

.
Подставим в (4):
;
.
Интегрируем:
.
Подставим в (П2):

.
Общий интеграл уравнения:
U ( x, y ) = const .
Объединяем две постоянные в одну.

Метод интегрирования вдоль кривой

Функцию U , определяемую соотношением:
dU = p ( x, y ) dx + q ( x, y ) dy ,
можно найти, если проинтегрировать это уравнение вдоль кривой, соединяющей точки ( x ₀ , y ₀) и ( x, y ) :
(7) .
Поскольку
(8) ,
то интеграл зависит только от координат начальной ( x ₀ , y ₀) и конечной ( x, y ) точек и не зависит от формы кривой. Из (7) и (8) находим:
(9) .
Здесь x ₀ и y ₀ – постоянные. Поэтому U ( x ₀ , y ₀) – также постоянная.

Пример такого определения U был получен при доказательстве свойства уравнения в полных дифференциалах:
(6) .
Здесь интегрирование производится сначала по отрезку, параллельному оси y , от точки ( x ₀ , y ₀ ) до точки ( x ₀ , y ) . Затем интегрирование производится по отрезку, параллельному оси x , от точки ( x ₀ , y ) до точки ( x, y ) .

В более общем случае, нужно представить уравнение кривой, соединяющей точки ( x ₀ , y ₀ ) и ( x, y ) в параметрическом виде:
x ₁ = s ( t ₁) ; y ₁ = r ( t ₁) ;
x ₀ = s ( t ₀) ; y ₀ = r ( t ₀) ;
x = s ( t ) ; y = r ( t ) ;
и интегрировать по t ₁ от t ₀ до t .

Наиболее просто выполняется интегрирование по отрезку, соединяющим точки ( x ₀ , y ₀ ) и ( x, y ) . В этом случае:
x ₁ = x ₀ + ( x – x ₀) t ₁ ; y ₁ = y ₀ + ( y – y ₀) t ₁ ;
t ₀ = 0 ; t = 1 ;
dx ₁ = ( x – x ₀) dt ₁ ; dy ₁ = ( y – y ₀) dt ₁ .
После подстановки, получается интеграл по t от 0 до 1 .
Данный способ, однако, приводит к довольно громоздким вычислениям.

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.

Автор: Олег Одинцов . Опубликовано: 10-08-2012 Изменено: 02-07-2015

Видео:Видеоурок "Уравнение в полных дифференциалах"Скачать

Тест с ответами: “Дифференциальные уравнения”

1. Уравнение, которое помимо функции содержит её производные:
а) дифференциальное уравнение +
б) иррациональное уравнение
в) тригонометрическое уравнение

2. Решите задачу Коши , . В ответе укажите значение его предел при :
а) 1
б) 0 +
в) 10

3. Порядок входящих в уравнение производных:
а) ограничен
б) может быть различен +
в) зависит от условия задачи

4. Дифференциальное уравнение порядка выше первого можно преобразовать в систему уравнений первого порядка, в которой число уравнений равно порядку исходного дифференциального уравнения, так ли это:
а) нет
б) да +
в) отчасти

5. Производные, функции, независимые переменные и параметры могут входить в уравнение в различных комбинациях или отсутствовать вовсе, кроме хотя бы одной производной, так ли это:
а) нет
б) да +
в) отчасти

6. Важнейшим вопросом для дифференциальных уравнений является существование и единственность их решения, так ли это:
а) нет
б) да +
в) отчасти

7. При решении дифференциальных уравнений ищется:
а) функция (семейство функций) +
б) число (несколько чисел)
в) оба варианта верны

8. После определения вида указанных постоянных и неопределённых функций решения становятся:
а) частными +
б) общими
в) практическими

9. Дифференциальное уравнение порядка выше первого можно преобразовать в систему уравнений первого порядка, в которой число уравнений равно порядку исходного дифференциального уравнения, так ли это:
а) нет
б) да +
в) отчасти

10. Решения дифференциальных уравнений подразделяются на:
а) теоретические
б) общие +
в) практические

11. Что является порядком дифференциального уравнения:
а) наивысший порядок входящих в него производных +
б) низший порядок входящих в него производных
в) средний порядок входящих в него производных

12. Решения дифференциальных уравнений подразделяются на:
а) дробные
б) частные +
в) цельные

13. Если дифференциальное уравнение является многочленом относительно старшей производной, то степень этого многочлена называется:
а) степенью дифференциального уравнения +
б) порядком дифференциального уравнения
в) объектом дифференциального уравнения

14. Решите задачу Коши , . В ответе укажите значение её решения при :
а) 5
б) 25
в) -25 +

15. Дифференциальное уравнение для функции от одной переменной:
а) обыкновенное дифференциальное уравнение +
б) простейшие дифференциальные уравнения первого порядка
в) дифференциальные уравнения в частных производных

16. Решите задачу Коши , . В ответе укажите значение её решения при :
а) 3
б) 2 +
в) 1

17. Одно из простейших применений дифференциальных уравнений — решение нетривиальной задачи нахождения траектории тела по известным проекциям ускорения, так ли это:
а) да +
б) нет
в) лишь отчасти

18. Найдите абсциссу точки пересечения прямой и решения уравнения , проходящего через точку :
а) 2
б) -1 +
в) 0

19. Класс дифференциальных уравнений первого порядка, наиболее легко поддающихся решению и исследованию:
а) дифференциальные уравнения в частных производных
б) обыкновенное дифференциальное уравнение
в) простейшие дифференциальные уравнения первого порядка +

20. Найдите решение уравнения удовлетворяющее начальному условию . В ответе укажите его предел при :
а) 4
б) -2
в) 2

21. Дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные производные:
а) дифференциальные уравнения в частных производных +
б) обыкновенное дифференциальное уравнение
в) простейшие дифференциальные уравнения первого порядка

22. Найдите решение уравнения удовлетворяющее начальному условию . В ответе укажите его значение при :
а) -4
б) 6 +
в) 4

23. Составьте дифференциальное уравнение семейства кривых :
а)
б)
в) +

24. Найдите решение уравнения удовлетворяющее начальному условию . В ответе укажите его значение при :
а) 1
б) -1 +
в) 10

25. Составьте дифференциальное уравнение семейства кривых :
а)
б)
в) +

26. Найдите решение уравнения удовлетворяющее начальному условию . В ответе укажите его значение при :
а) 1
б) -1 +
в) -10

27. Составьте дифференциальное уравнение семейства кривых :
а) +
б)
в)

28. Найдите решение уравнения , удовлетворяющее начальному условию . В ответе укажите его значение при :
а) 31
б) 51
в) 101 +

29. Найдите решение уравнения , удовлетворяющее начальному условию. В ответе укажите его значение при :
а) 30 +
б) 10
в) 20

30. Найдите решение уравнения , удовлетворяющее начальному условию . В ответе укажите его значение при :
а) 2
б) 1 +
в) 3

📽️ Видео

Дифференциальные уравнения в полных дифференциалах (часть 1)Скачать

Дифференциальные уравнения не разрешенные относительно производной | poporyadku.schoolСкачать

Дифференциальные уравнения в полных дифференциалах| poporyadku.schoolСкачать

Видеоурок "Интегрирующий множитель"Скачать

Восстановление функции по полному дифференциалу. Дифференциальное уравнение в полных дифференциалах.Скачать

ДУ Уравнения, не разрешенные относительно производнойСкачать

13. Как решить дифференциальное уравнение первого порядка?Скачать

Курс по ОДУ: Уравнения, не разрешённые относительно производной | Занятие 7Скачать

Составить дифференциальные уравнения семейств линийСкачать

6. Особые решения ДУ первого порядкаСкачать

Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать