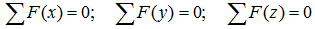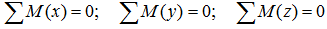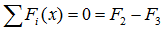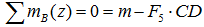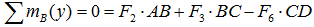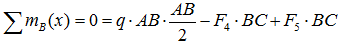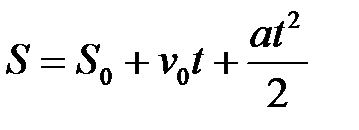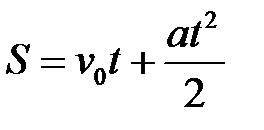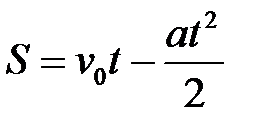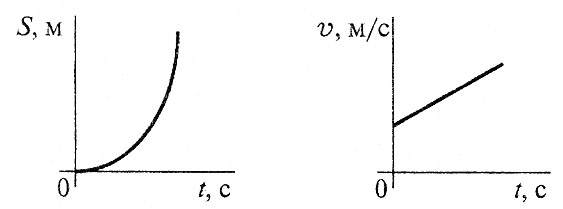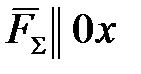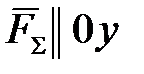- Плоская система сходящихся сил
- Геометрический способ определения равнодействующей плоской системы сходящихся сил
- Геометрическое условие равновесия плоской системы сходящихся сил
- Проекция силы на оси координат
- Аналитический способ определения равнодействующей плоской системы сил
- Аналитические условия равновесия плоской системы сходящихся сил
- iSopromat.ru
- Пример составления уравнений равновесия
- Суммы проекций сил
- Суммы моментов
- Решение задач, контрольных и РГР
- Ключи к тестам по «Технической механике»
- Момент силы. Условия равновесия рычага
- п.1. Устройство и виды рычагов
- п.2. Момент силы
- п.3. Правило моментов для двух сил
- п.4. Правило моментов для нескольких сил
- п.5. Применение рычагов в быту и технике
- п.6. Задачи
- п.7. Лабораторная работа №9. Проверка условия равновесия рычага
- 🔍 Видео
Видео:Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать

Плоская система сходящихся сил
Геометрический способ определения равнодействующей плоской системы сходящихся сил
Система сил, линии действия которых лежат в одной плоскости и все пересекаются в одной точке, называется плоской системой сходящихся сил.
Теорема
Плоская система сходящихся сил в общем случае эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих.
Пусть дана плоская система трех сил F1 , F2 и F3 , линии действия которых сходятся в точке А (см. рисунок а) .

R = F1 + F2 .
Пользуясь той же аксиомой параллелограмма, сложим равнодействующую R с силой F3 :
где FΣ – равнодействующая данной системы трех сил.
Аналогичные рассуждения можно провести для любого количества сходящихся сил, в результате чего получим:
FΣ = F1 + F2 + F3 +…+ Fn .
Сокращенно это равенство можно записать так:
FΣ = ΣFi , где i – все целые числа от единицы до n .
Очевидно, что построения, выполненные на рисунке a , можно заменить более простым, как показано на рисунке b . Многоугольник АВСD называют силовым многоугольником. Сторона AD , соединяющая начало первого с концом последнего вектора, называется замыкающей стороной.
Необходимо помнить, что стрелки векторов слагаемых сил образуют определенное направление обхода по контуру силового многоугольника, а замыкающая сторона, определяющая модуль и направление равнодействующей, имеет стрелку, направленную против обхода (см. рисунок b) .
Если определить равнодействующую из силового многоугольника с помощью геометрии и тригонометрии, то такой способ будет называться геометрическим.
Если сделать чертеж силового многоугольника в определенном масштабе, то равнодействующая определится простым измерением замыкающей стороны с последующим умножением на масштаб. Такой способ нахождения равнодействующей называется графическим.
Порядок сложения векторов при построении силового многоугольника на величину равнодействующей не влияет, так как векторная сумма от перемены мест слагаемых не меняется.
Геометрическое условие равновесия плоской системы сходящихся сил
При построении силового многоугольника возможен случай, когда конец последнего вектора совпадает с началом первого. В этом случае замыкающей стороны не будет, и такой силовой многоугольник называется замкнутым.
Очевидно, что равнодействующая FΣ системы сходящихся сил, образующих замкнутый силовой многоугольник, равна нулю, т. е. система сил находится в равновесии. Отсюда вытекает условие, при котором плоская система сходящихся сил будет находиться в равновесии. Это условие выражается равенством:
и формулируется так: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник был замкнут.
Условия равновесия, записанные в виде равенств, содержащих неизвестные величины, называются уравнениями равновесия.
Применяя геометрическое условие равновесия, удобно решать задачи, в которых на тело действуют три силы, так как в этом случае замкнутый силовой многоугольник представляет собой треугольник.
Решение большинства задач статики проводят в три этапа:
— выбирают тело, равновесие которого будет рассматриваться;
— отбрасывают связи, заменяя их реакциями, и устанавливают, какая система сил действует на тело;
— пользуясь условиями равновесия, находят неизвестные величины.
При решении задач статики следует строго соблюдать правило: размерности и единицы величин всех слагаемых и обеих частей равенства должны быть одинаковыми.
В сомнительных случаях целесообразно использовать это правило для проверки правильности хода решения задач, для чего следует подставить в слагаемые проверяемого равенства единицы всех входящих в них величин и, произведя возможные сокращения, сравнить полученные единицы правой и левой частей.
Пример решения задачи
В качестве примера решения задачи с использованием изложенных выше методов, определим натяжение веревки F и силу давления шара P на стену, если сила тяжести шара равна G .
Рассмотрим условие равновесия шара. Применив принцип освобождаемости, отбросим связи и заменим их реакциями. Реакция N гладкой стены перпендикулярна стене и проходит через центр шара (так как шар однородный, его геометрический центр совпадает с центром тяжести).
Реакция F веревки направлена вдоль линии натяжения веревки и тоже проходит через центр шара (согласно теореме о равновесии трех непараллельных сил). Применим к системе сил уравнение равновесия:
ΣFi = 0 , или G + N + R = 0.
Строим замкнутый силовой треугольник, начиная с изображения в произвольном масштабе вектора известной силы G (см. рисунок) . Направление обхода треугольника (т. е. направление стрелок) определяется направлением этой силы. Из построенного силового треугольника получим соотношения:
N = G tg α ; R = G/cos α
Искомая сила давления P шара на стену, согласно аксиоме взаимодействия, по модулю равна реакции N стены, но направлена в противоположную сторону.
Натяжение веревки F равно по модулю ее реакции R .
Эту же задачу можно решить, разложив силу тяжести шара G по реальным направлениям (направлениям реакций) на составляющие P (сила давления шара на стену) и F (натяжение веревки) , причем согласно аксиоме взаимодействия:
Из построенного параллелограмма (см. рисунок) легко определить искомые величины.
Такой метод решения задачи называют методом разложения силы.
Проекция силы на оси координат
В тех случаях, когда на тело действует более трех сил, а также когда неизвестны направления некоторых сил, удобнее при решении задач пользоваться не геометрическим, а аналитическим условием равновесия, которое основано на методе проекций сил на оси координат.
Проекцией силы на ось называют отрезок оси, заключенный между двумя перпендикулярами, опущенными на ось из начала и конца вектора силы.
На приведенном ниже рисунке видно, что проекции силы P на оси x и y можно определить при помощи тригонометрических функций:
Px = Pcos α, Py = Psin α .
Проекция силы на ось есть величина алгебраическая, которая может быть положительной или отрицательной, что устанавливается по направлению проекции — проекция, направленная в положительном направлении оси считается положительной, в противном случае — отрицательной.
Возможны два частных случая:
— если сила перпендикулярна оси, то ее проекция равна нулю (сила проецируется в точку) ;
— если сила параллельна оси, то она проецируется на ось в натуральную величину.
Зная проекции силы на координатные оси, можно определить ее величину (модуль) , используя теорему Пифагора, учитывая, что проекции являются катетами прямоугольного треугольника, а сама сила — гипотенузой.
Направляющий тангенс угла между вектором силы P и осью x можно определить из отношения:
tgα = Py/Px .
Отметим, что силу P можно представить, как равнодействующую двух составляющих сил Px и Py , параллельных осям координат, но эти составляющие не будут являться проекциями силы по определению, поскольку сила (в т. ч. и составляющая силы) есть величина векторная, а проекция — алгебраическая.
Аналитический способ определения равнодействующей плоской системы сил
Пусть дана плоская система сходящихся сил F1, F2, F3, F4. Fn .
Равнодействующая этой системы FΣ = ΣFi .
В плоскости действия данной системы сил выберем ось координат и спроецируем данные силы и их равнодействующую на эту ось. Из математики известно свойство проекции векторной суммы, на основании которого можно утверждать, что проекция равнодействующей на ось равна алгебраической сумме проекций составляющих сил на ту же ось, т. е. FΣx = ΣFix .
Правую часть этого равенства можно представить упрощенно: FΣx = ΣX .
Для того чтобы определить равнодействующую любой плоской системы сходящихся сил, спроецируем их на оси координат x и y , алгебраически сложим проекции всех сил и найдем таким образом проекции равнодействующей:
Зная проекции, определим модуль и направление равнодействующей:
Модуль равнодействующей:
FΣ = √(FΣx 2 + FΣy 2 ) (здесь и далее √ — знак корня);
Направляющий тангенс угла между вектором FΣ и осью x :
Линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил.
Аналитические условия равновесия плоской системы сходящихся сил
Если данная плоская система сходящихся сил находится в равновесии, то равнодействующая такой системы, а значит и проекции равнодействующей на оси координат равны нулю.
Математически это выражение можно записать так:
Учитывая, что FΣx = ΣX; FΣy = ΣY , получаем равенства, выражающие аналитические условия равновесия плоской системы сходящихся сил:
Формулируется это условие следующим образом: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраическая сумма проекций этих сил на каждую из двух координатных осей равнялась нулю.
С помощью уравнений равновесия можно определить два неизвестных элемента данной системы сил, например модуль и направление одной силы или модули двух сил, направления которых известны и т. п.
Выведенные условия равновесия справедливы для любой системы координат, но для упрощения расчетов рекомендуется оси координат по возможности выбирать перпендикулярными неизвестным силам, чтобы каждое уравнение равновесия содержало одно неизвестное.
Когда направление искомой силы неизвестно, ее можно разложить на две составляющие по заданным направлениям, обычно по направлениям координатных осей; по найденным двум составляющим легко определяется неизвестная сила.
Если при решении задач аналитическим способом искомая реакция получается отрицательной, то это означает, что действительное ее направление противоположно направлению, принятому при расчетах.
Видео:Статика. Момент сил. Условия равновесия тел | Физика ЕГЭ, ЦТ, ЦЭ | Физика для школьниковСкачать

iSopromat.ru
Уравнения равновесия (статики) характеризуют неподвижность заданной системы нагруженной комплексом внешних усилий.
При решении задач теоретической механики и сопротивления материалов (например, при определении опорных реакций или внутренних силовых факторов) исходя из условия неподвижности системы или ее частей, записываются уравнения равенства нулю сумм проекций всех сил на оси выбранной системы координат
что следует из условия отсутствия перемещения системы вдоль этих осей, и сумм моментов относительно произвольных точек системы
из условия отсутствия ее вращения относительно указанных осей.
Надо отметить что в случае действия плоской системы сил можно получить только три уравнения статики, а линейная схема нагружения позволяет записать лишь одно уравнение.
Видео:1 Решение задачи графическим и аналитическим методомСкачать

Пример составления уравнений равновесия
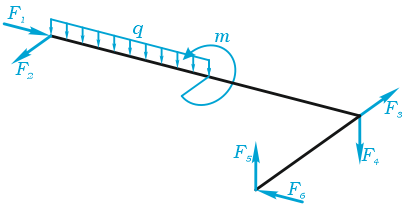
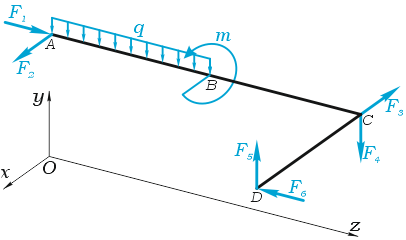
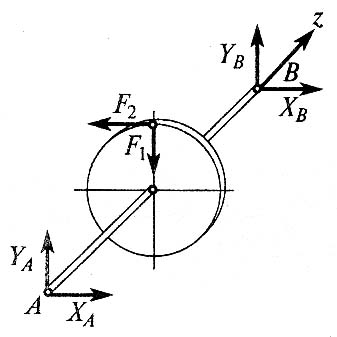
В качестве примера, рассмотрим общий случай пространственного нагружения, где комплекс усилий, включающий сосредоточенные силы F1-F6, равномерно распределенную нагрузку q, и момент m расположенный в плоскости перпендикулярной длинному стержню, удерживает L-образную систему в равновесии.
Обозначим характерные точки системы буквами A, B, C и D, зададим положение трехмерной системы координат xyz и запишем уравнения равновесия.
Суммы проекций сил
Сумма проекций всех сил на ось x (с учетом правила знаков для сил):
здесь при записи силы от распределенной нагрузки ее интенсивность q умножается на ее длину AB.
Суммы моментов
Суммы моментов всех нагрузок, например, относительно точки B (с учетом правила знаков для моментов):
- в плоскости xOy:
- в плоскости xOz:
- в плоскости yOz:
Из полученных шести уравнений можно определить не более шести неизвестных усилий.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Видео:Урок 71. Простейшие задачи на правило силСкачать
Решение задач, контрольных и РГР
По желанию можете добавить файл или фото задания
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ
— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку
Видео:Система сходящихся силСкачать
Ключи к тестам по «Технической механике»
КОМПЛЕКТ ТЕСТОВ
для оценки результатов освоения учебной дисциплины
основной профессиональной образовательной программы СПО
Инструкция по выполнению работы
Уровень А включает 25 заданий с выбором ответа. К каждому заданию дается четыре ответа, из которых только один правильный.
Уровень В состоит из 50 заданий с кратким ответом или выбором одного правильного ответа. К каждому заданию запишите краткий ответ на вопрос, окончание предложения или пропущенные слова.
Уровня С включает 25 заданий. Для выполнения заданий необходимо написать развернутый ответ в произвольной форме.
За каждый правильный ответ в зависимости от сложности задания дается один или более баллов. Баллы, полученные вами за все выполненные задания, суммируются.
Уровень — Уровень А
А1.Что изучает кинематика?
А) Движение тела под действием приложенных к нему сил.
Б) Виды равновесия тела.
В) Движение тела без учета действующих на него сил.
Г) Способы взаимодействия тел между собой.
А2.Какого способа не существует для задания движения точки (тела)?
А) Способность конструкции выдерживать заданную нагрузку не разрушаясь и без появления остаточных деформаций.
Б) Способность конструкции сопротивляться упругим деформациям.
В) Способность конструкции сохранять первоначальную форму упругого равновесия.
Г) Способность конструкции не накапливать остаточные деформации.
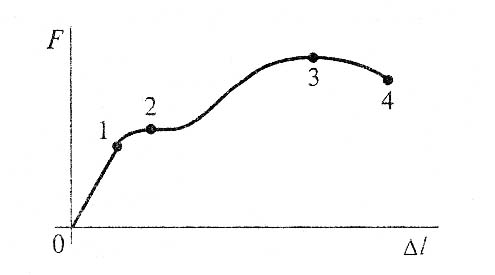
А4.Как называется график зависимости между растягивающей силой и соответствующим удлинением образца материала?
А5.Какого вида расчетов не существует в «сопротивлении материалов»?
А) Проектного расчета
Б) Расчета на допустимую нагрузку
В) Проверочного расчета
Г) Математического расчета
А6.Как называется брус, работающий на изгиб?
А7.Какого вида изгиба не существует?
А8.Для наиболее наглядного представления о характере изменения внутренних силовых
факторов при нагрузках на брус принято строить…
А9.Что называется силой?
А) Давление одного тела на другое.
Б) Мера воздействия одного тела на другое.
В ) Величина взаимодействия между телами.
Г) Мера взаимосвязи между телами (объектами).
А10.Назовите единицу измерения силы?
А11. Какой прибор служит для измерения силы?
А12.В какой точке диаграммы растяжения на образце образуется шейка?
А13.Равнодействующей двух сил приложенных в одной точке будет…
а) сторона параллелограмма
б) диагональ параллелограмма
в) высота треугольника
А14.Как направлена реакция связи гладкая опора?
а) параллельно опоре
б) под углом к опоре
в) перпендикулярно опоре
А15.Допускаемое напряжение это ____________ напряжение при котором материал должен нормально работать.
А16.Две силы считаются уравновешенными, если они находятся на одной прямой, _________________ .
а) равны по модулю и противоположно направлены
б) противоположно направлены
в) направлены в одну сторону
г) обе равны нулю
А17.Как называется тело у которого одно измерение размера много меньше двух других?
А18.Плоская система сходящихся сил находится в равновесии, если алгебраические суммы проекций всех сил на оси ОХ и ОУ равны __________________ .
в) минус единице
г) имеют переменное значение
А19.Систему из двух параллельных сил равных по значению и противоположно направленных называют ________________ .
в) удвоенными силами
г) направленными силами
А20.Чему равен момент пары сил?
а) произведению двух сил
б) расстоянию между силами
в) произведению модуля силы на расстояние между силами
А21.Главный вектор отличается от равнодействующей плоской системы произвольно расположенных сил _____________ .
б) ничем, это одно и то же
А22.Можно ли суммировать моменты сил приложенные к телу в одной плоскости?
г) можно, если они имеют одинаковый знак
А23.Может ли быть момент силы отрицательным числом?
б) всегда положителен
г) нет, т.к. равен нулю
А24.В каких случаях проекция вектора равна по значению самому вектору?
а) если вектор перпендикулярен оси
б) если вектор расположен под углом к оси
в) если вектор параллелен оси
г) если вектор и ось составляют острый угол
А25.Может ли проекция вектора иметь отрицательное значение?
б) может, если вектор равен единице
г) проекция всегда положительна по определению
Уровень — Уровень В
В1.Как называются тела, ограничивающие перемещение других тел?
В2.При каких условиях равнодействующая сила равна нулю?
А) если вектор равнодействующей силы вписывается в окружность
Б) если вектор равнодействующей силы соединяет начало первого силового вектора с концом последнего
В) если многоугольник составляющих сил является замкнутым
Г) если можно составить из всех составляющих сил квадрат
В3.Силы, с которыми два тела действуют друг на друга, всегда равны, находятся на одной прямой и _________________ .
А) направлены в одну сторону
Б) направлены в противоположные стороны
В) направлены под углом друг к другу
Г) смотрят друг на друга
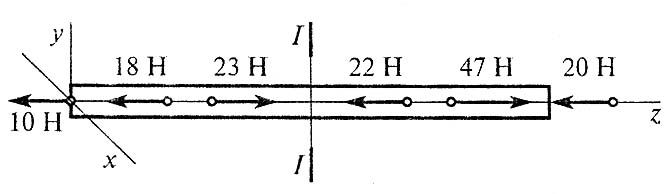
В4.Установить вид нагружения в сечении I–I
Б) брус растянут
В5.Как называется и обозначается напряжение, при котором деформации растут при постоянной нагрузке?
А) Предел текучести, sТ
б) Предел прочности, sВ
в) Допускаемое напряжение, [s]
г) Предел пропорциональности, sпц
В6.В каких единицах измеряется механическое напряжение в системе единиц СИ?
В7.Прямой брус нагружен силой F. Какую деформацию получил брус, если после снятия нагрузки форма бруса восстановилась до исходного состояния?
| L0 |
| F |
В8.Закон вращательного движения тела φ = 0,68t 3 + t . Определить ω в момент t = 1 с.
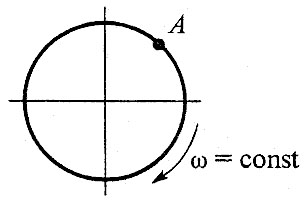
В9.Какие ускорения возникнут в точке А при равномерном вращении колеса?
В10.Закон вращательного движения тела φ = 0,25t 3 + 4t . Определить вид движения.
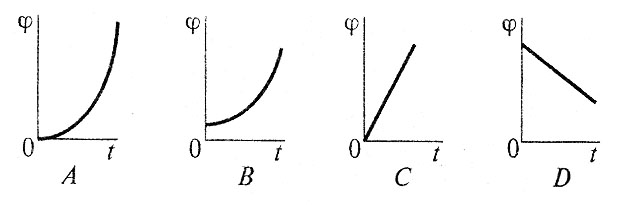
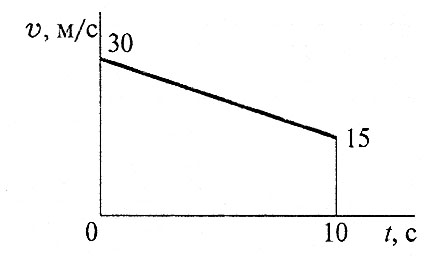
В12.По графику скоростей определить вид движения на третьем участке
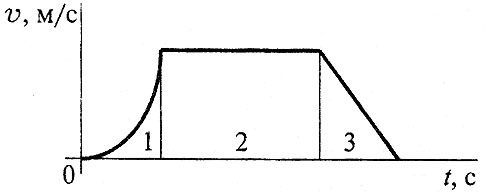
В13.По приведенным кинематическим графикам определить соответствующий закон движения точки.
Б)
В)
Г)
В14.В каком случае для определения положения центра тяжести необходимо определить две координаты расчетным путем?
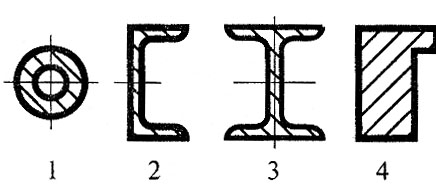
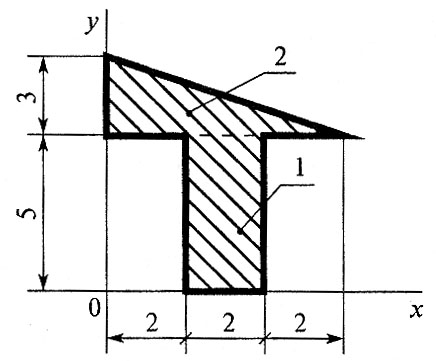
В15.Что произойдет с координатами хС и уС, если увеличить величину основания треугольника до 90 мм?
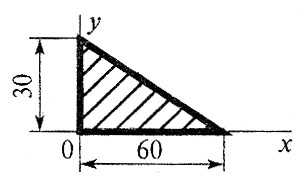
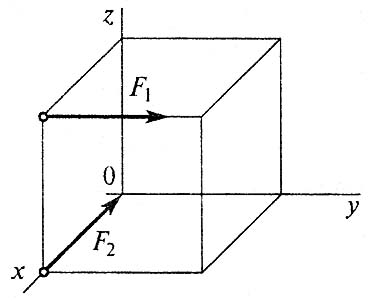
В16.Определить сумму моментов сил относительно 0z, если F1=2 Н; F2=13 Н, а сторона куба 0,5 м
В) 0
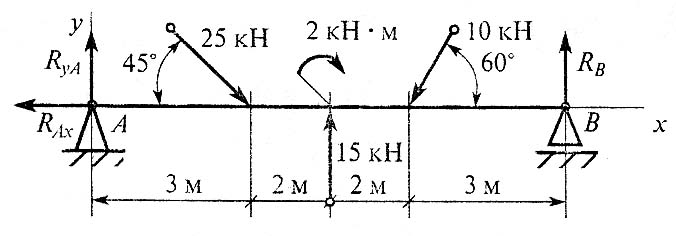
В17.Какие уравнения равновесия нужно использовать, чтобы найти XA?
В18. Тело равномерно вращается вокруг неподвижной оси. Чему равны главный вектор и главный момент системы сил?
В19.Какое уравнение равновесия можно использовать, чтобы сразу найти MA, зная F, q, α.
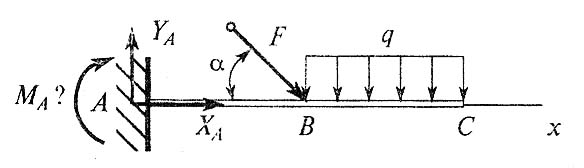
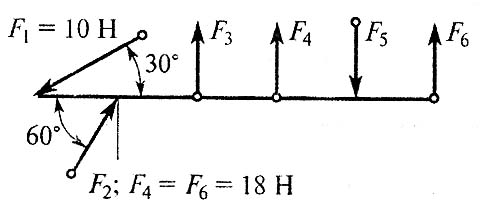
В21.Как изменится момент пары сил при повороте сил на угол равный 30º?
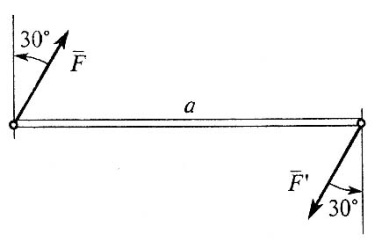
А) уменьшится в 1,15 раза
Б) увеличится в 1,15 раза
В) увеличится в 1,5 раза
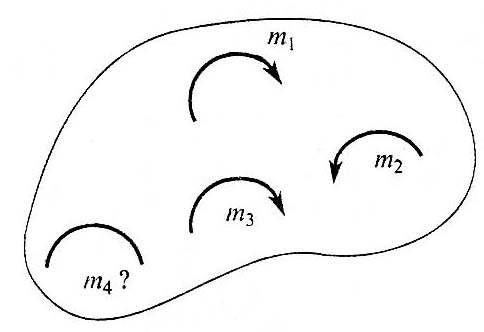
В22.. Тело находится в равновесии. Определить величину момента пары М4, если
М1=15 Н·м; М2=8 Н·м; М3=12 Н·м; М4=?
| М1 |
| М2 |
| М3М3 3 |
| М4 ? |




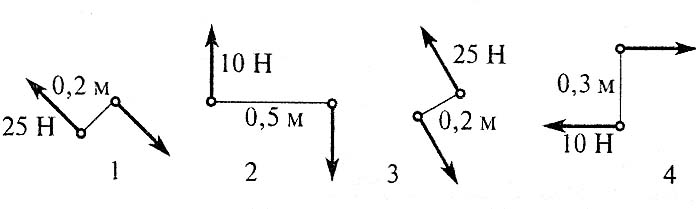
В23.Какие из изображенных пар сил эквиваленты?
В24.Как направлен вектор равнодействующей силы, если известно, что его проекции Fх=15 Н; Fу= -20 Н?
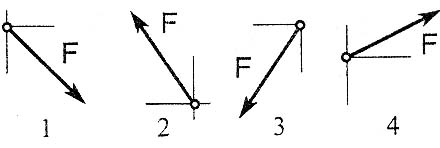
В25.Выбрать выражение для расчета проекции силы F1 на ось 0у.
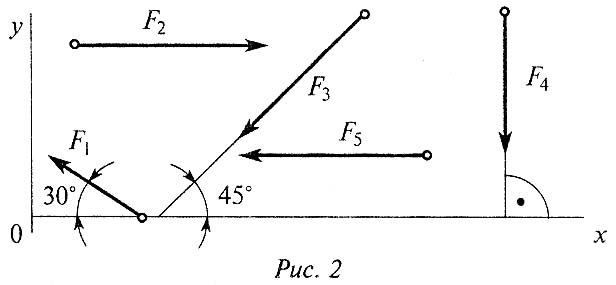
В26.При равномерном и прямолинейном движении тела главный вектор равен _________________ .
Б) главному моменту
В2 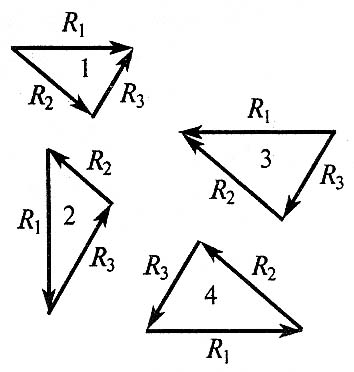
А) на границе тела
Б) в центре координат
В) на оси симметрии
Г) слева от оси симметрии
В28.Изменится ли положение центра тяжести тела, если его повернуть на 90 градусов?

в) зависит от массы тела
г)зависит от габаритных размеров тела
В29.Нормальная составляющая ускорения точки an характеризует изменение скорости по______________________.
В30.Движениеточки считается равномерным, если постоянна её__________________.

В32.Упругими деформациями называются деформации, которые полностью исчезают при снятии ________________.
В33.В отличии от внешних сил, силы упругости это_________________силы.
В34.Скольковнутренних силовых факторов влияет на деформацию тела? ________________________.
В35.Какой силовой фактор вызывает растяжение бруса? _______________________.
В36.Как распределены напряжения по сечению при растяжении и сжатии?
В37.График распределения внутренних сил по оси бруса называется _________________.
В38.Деформации, которые полностью не исчезают при снятии нагрузки, называют
В39.Метод сечения заключается в мысленном рассечении тела _____________ и рассмотрении равновесия любой из отсеченных частей.
В40.Модуль упругости характеризует ___________________ материала.
В41.Две силы F1=30Н и F2=40Н приложены к телу под углом 90° друг другу. Чему равна их равнодействующая?
В42.Момент силы считается отрицательным, когда тело под действием силы вращается __________________ часовой стрелки.
В43.Движение твердого тела при котором всякая прямая линия на теле при движении остается параллельной своему первоначальному положению называтся _______________.
В44.В задачах статики для абсолютно твердых тел нагрузку ________________ можно заменить сосредоточенной.
В45.Изменение размеров и формы тела под действием внешних сил называется _____________.
В46.Часть теоретической механики, изучающая условия, при которых тело находится в равновесии, называется __________________.
В47. Если вектор силы находится под углом α к оси, то _________силы на ось равна произведению силы на Соs α.
В48.Произведение модуля ___________ на её плечо, называется моментом пары.
В49.Если главный ___________ и главный момент равны нулю, то система сил
находится в равновесии.
В50. Геометрическая точка, которая может располагаться в самом теле или вне него называется _____________тяжести.
Уровень — Уровень С
С1. Составлено уравнение для расчета реакции в опоре А. Какого слагаемого в уравнении не хватает?
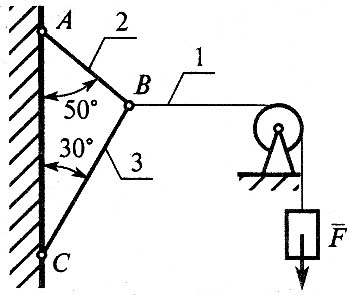
С2.Груз находится в равновесии. Указать, какой из силовых треугольников для шарнира B построен верно.
в) 3
С3.Точка М движется равномерно по кривой радиуса r. Выбрать направление силы инерции.
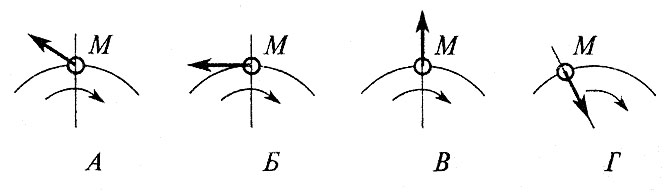
С4.По графику скоростей точки определить путь, пройденный за время движения.
С5.Определить координаты центра тяжести фигуры 2:
а) 2; 1
А)
Б)
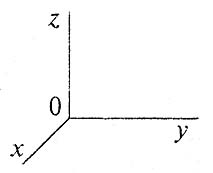
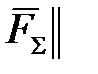
Г) 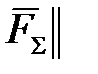
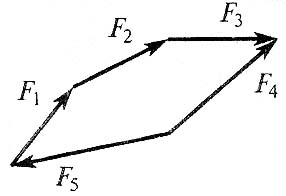
С7.Какой вектор силового многоугольника является равнодействующей силой?
в) F5
С8.Какие из сил данной системы можно назвать уравновешенными?
| F2 |
| F1b F2 |
| F3 |
| F4 |
| F5 |
| F6 |
б) F2 и F5
г) Уравновешенных сил нет
С9.Автомобиль движется по круглому арочному мосту r=50 м согласно уравнению S=10t. Определить полное ускорение автомобиля через 3 с движения
С10.Составляющие главного вектора R и главного момента M внутренних
сил по координатным осям X; Y; Z называют ____________ .
а) нормальными и касательными напряжениями;
б) внутренними силовыми факторами
в) напряженным состоянием в точке;
г) тензором напряжений
С11.Пластичностью называется свойство материала_______________ .
а) сопротивляться проникновению в него другого более твердого тела;
б) сохранять некоторую часть деформации после снятия нагрузки;
в) восстанавливать свою форму и размеры после снятия нагрузки;
г) сопротивляться разрушению.
С12.Нагрузки, числовое значение, направление и место приложения которых остаются постоянными или
меняются медленно и незначительно называются __________
С13. К передачам трением относятся________________
а) фрикционные, ременные
б) зубчатые, червячные
в) ременные, цепные
С14. Основные достоинства фрикционной передачи ______________.
а) бесшумность и плавность работы
б) постоянство передаточного отношения
в) нагрузка на опоры
г) низкая стоимость и доступность материала
С15. Центр тяжести прямоугольника находится на пересечении _______________ .
С16 Ускорение точки в криволинейном движении раскладывается на ____________ .
а) поступательное и вращательное
б) нормальное и касательное
в) прямолинейное и криволинейное
С17.При поступательном движении все точки твердого тела имеют ___________ .
а) разные траектории, скорости и ускорения
б) переменные траектории, скорости и ускорения
в) одинаковые траектории, скорости и ускорения
С18.Установите соответствие единиц измерения.
С19.Нагрузки, которые многократно меняют свое значение или знак и значение, называются______________ .
С20.Нагрузки, которые меняют свое значение в короткий промежуток времени, называют __________________.
С21.Если в поперечном сечении возникает только продольная сила N, то имеем деформацию _______________ .
а) сжатие, растяжение
С22.Если в поперечном сечении возникает только один внутренний силовой фактор — поперечная сила Q, то это деформация _______________ .
а) сжатие, растяжение
С23 Если в поперечном сечении возникает только один внутренний силовой фактор — крутящий момент, то это деформация ______________
С24.Внутренняя сила, отнесенная к единице площади сечения, называется _______________ .
в) изгибающий момент
С25.Допускаемое напряжение это _____________ напряжение, при котором материал должен нормально работать
Ключи к тестам по «Технической механике»
Видео:4.3 Формула определения равнодействующей силыСкачать

Момент силы. Условия равновесия рычага
п.1. Устройство и виды рычагов
 | Рычаг – это твёрдое тело, которое может вращаться вокруг неподвижной опоры. |
Рычаг состоит из перекладины и опоры.
Точка опоры делит перекладину рычага на два плеча рычага.
Назначение рычага – получить выигрыш в силе или расстоянии.
Если к плечу рычага достаточно приложить меньшую силу, то переместить конец рычага придётся на бóльшее расстояние: выигрыш в силе оборачивается проигрышем в расстоянии.
И наоборот, если удаётся сократить перемещение конца рычага, придётся приложить бóльшую силу: выигрыш в расстоянии оборачивается проигрышем в силе.
В зависимости от взаимного расположения точки опоры и нагрузки различают три вида рычагов.
Рычаг 1-го рода  Опора располагается между точками приложения сил  Даёт выигрыш в силе | Рычаг 2-го рода  Точки приложения сил располагаются по одну сторону от опоры, нагрузка приложена между точкой опоры и точкой приложения силы  Даёт выигрыш в силе |
Рычаг 3-го рода   Точки приложения сил располагаются по одну сторону от опоры, усилие приложено между точкой опоры и нагрузкой. Проигрыш в силе – выигрыш в расстоянии | |
п.2. Момент силы
Чтобы найти плечо силы, нужно из точки опоры провести перпендикуляр на линию действия силы.
На рисунке (l_1) – плечо силы (F_1, l_2) — плечо силы (F_2).
Силы вращают рычаг вокруг точки опоры – по часовой или против часовой стрелки.
Ось вращения проходит через точку опоры перпендикулярно плоскости вращения.
На рисунке сила (F_1) вращает рычаг против часовой стрелки, а сила (F_2) — по часовой стрелке.
Момент силы определяется не для всего тела, а для некоторой его точки, удалённой от центра (оси) вращения. Эта величина имеет смысл только для вращающихся тел.
п.3. Правило моментов для двух сил
 | $$ F_1l_1=F_2l_2 $$ |
п.4. Правило моментов для нескольких сил
 | Силы (F_1, F_2, F_3) вращают рычаг против часовой стрелки, а сила (F_4) — по часовой стрелке. Поэтому: $$ F_1l_1+F_2l_2+F_3l_3=F_4l_4 $$ |
п.5. Применение рычагов в быту и технике
Рычаги первого рода
 Весы Предмет, вес которого нужно измерить, — это нагрузка, а гиря создает усилие. Они равны, так как находятся на одном расстоянии от точки опоры. |  Рычажные весы Точка опоры смещена относительно центра. Грузило передвигается по основанию, пока не уравновесит взвешиваемый объект. |
 Гвоздодёр Усилие ручки увеличивается плечом и вытаскивает гвоздь. Нагрузкой здесь является сопротивление гвоздя. |  Ручная тележка Небольшое усилие, прикладываемое к ручкам тележки, позволяет поднимать тяжелый груз. |
 Плоскогубцы Составной рычаг, пара простых рычагов, соединенных в точке опоры. Нагрузка — сопротивление предмета захвату инструментом. |  Ножницы Составной рычаг первого рода, развивают мощное режущее действие очень близко к месту крепления. Нагрузка — сопротивление материала лезвиям. |
Рычаги второго рода
 Тачка Небольшое усилие, приложенное к ручкам тачки, поднимает тяжелый груз, расположенный ближе к колесу. |  Открывалка Давление на ручку преодолевает сопротивление крышки бутылки. |  Щипцы для орехов Составной рычаг второго рода. Нагрузка — сопротивление скорлупы. |
Рычаги третьего рода
 Молоток Точка опоры — плечевой сустав (рука — продолжение рукоятки), а нагрузка — сопротивление дерева. Во время удара по гвоздю головка молотка двигается быстрее, чем рука с рукояткой. |  Удочка Одна рука прикладывает усилие для движения удочки, вторая становится точкой опоры. Нагрузка — это вес рыбы, который поднимается на большую высоту легким движением руки. |
 Пинцет Составной рычаг третьего рода. На кончиках пинцета усилие меньше, чем со стороны пальцев, так что можно захватывать хрупкие предметы. Нагрузка — сопротивление предмета. | |
п.6. Задачи
Задача 1. Для каждого положения тела укажите плечо силы.
При необходимости достраиваем линию действия силы и опускаем на неё перпендикуляр из точки опоры. Этот перпендикуляр и есть искомое плечо.
Задача 2. Грузы уравновешены на рычаге. Отношение плеч рычага 1:5. Масса большего груза 2,5 кг. Найдите массу меньшего груза.
По правилу моментов begin F_1l_1=F_2l_2 end На обоих концах рычага действуют силы тяжести: $$ F_1=m_1g, F_2=m_2g $$ Получаем: begin m_1gl_1=m_2gl_2\[7pt] m_2=frac end Подставляем: $$ m_2=2,5cdot frac 15=0,5 (text) $$ Ответ: 0,5 кг
Задача 3. На концах рычага действуют силы 15 Н и 60 Н, направленные вниз. Рычаг находится в равновесии. Расстояние между точками приложения сил 1 м. Где расположена точка опоры?
По правилу моментов begin F_1l_1=F_2l_2. end Получаем систему уравнений begin left< begin 15l_1=60l_2 \ l_1+l_2=1 end right. Rightarrow left< begin l_1=4l_2 \ l_1+l_2=1 end right. Rightarrow left< begin l_1=4l_2 \ 4l_2+l_2=1 end right. Rightarrow \[7pt] Rightarrow left< begin l_1=4l_2 \ 5l_2=1 end right. Rightarrow left< begin l_1=0,8 \ l_2=0,2 end right. end Ответ: 0,8 м от точки приложения первой силы и 0,2 м от точки приложения второй силы.
Задача 4*. К балке, расположенной на двух опорах А и В подвешен груз массой 500 кг. Расстояние от точки подвеса груза к одному из концов балки в 4 раза больше, чем к другому. С какой силой балка давит на каждую из опор? Примите (gapprox 10 text^2). Ответ запишите в килоньютонах.
Сила тяжести (F_<text>=mg), направленная вниз, уравновешивается силами реакции опор (F_A) и (F_B), направленными вверх. begin F_A+F_B=mg end По правилу моментов при равновесии begin F_Acdot OA=F_Bcdot OB=F_Bcdot 4OARightarrow F_A=4F_B \[7pt] F_A+F_B=5F_B=mgRightarrow F_B=frac end Получаем: begin F_B=frac=1000 text=1 text, F_A=4cdot 100=4000 text=4 text end Ответ: 4 кН и 1 кН
п.7. Лабораторная работа №9. Проверка условия равновесия рычага
Цель работы
Исследовать условия равновесия рычага под действием двух параллельных сил.
Рычаг – это твёрдое тело, которое может вращаться вокруг неподвижной опоры.
В работе используется рычаг 1-го рода, в котором опора располагается между точками приложения сил.
Плечо силы – это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг. Чтобы найти плечо силы, нужно из точки опоры провести перпендикуляр на линию действия силы.
Момент силы – это произведение силы, вращающей тело, на её плечо: (M=Fl).
Правило моментов для двух сил
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по ходу часовой стрелки, равен моменту силы, вращающей его против хода часовой стрелки.
 | begin M_1=M_2\[7pt] F_1l_1=F_2l_2 end |
В работе используется лабораторный рычаг с отверстиями диаметром 4 мм, находящимися на расстоянии 5 см друг от друга. Отверстий нечетное количество; центральное отверстие (центр тяжести) используется для подвеса рычага на штативе в положении равновесия. Абсолютную погрешность определения плеча на данном рычаге принимаем равной половине диаметра отверстия $$ Delta l=frac D2=2 text $$
Для измерения веса груза используется динамометр с ценой деления $$ d=0,1 text. $$
Абсолютная погрешность определения веса $$ Delta_F=frac d2=0,05 text. $$
Относительные погрешности измерений: $$ delta_l=frac, delta_F=frac, delta_M=delta_l+delta_F $$
Абсолютная погрешность определения момента силы $$ Delta_M=Mcdot delta_M $$
Приборы и материалы
Лабораторный рычаг, штатив, стержень, динамометр, набор грузов.
Ход работы
1. Закрепите стержень в штативе, наденьте на него рычаг. Если стержень проходит через центральное отверстие рычага, он находится в равновесии.
2. Подвесьте три груза на динамометре, запишите их вес (F_1).
3. Подвесьте грузы слева от оси вращения рычага на расстоянии 5 см.
4. С помощью динамометра определите, какую силу нужно приложить на расстоянии 15 см справа от оси вращения, чтобы удерживать рычаг в равновесии.
5. Как направлены в этом случае силы, действующие на рычаг? Запишите длину плеч этих сил.
6. Найдите моменты сил (M_1) и (M_2), их относительные и абсолютные погрешности.
7. Вычислите отношение сил (frac) и плеч (frac) для этого случая, погрешности их определения.
8. Сделайте выводы.
Результаты измерений и вычислений
| (F_1, text) | (l_1, text) | (F_2, text) | (l_2, text) | (F_1/F_2) | (l_2/l_1) |
| 2,9 | 5 | 1,0 | 15 | 2,9 | 3,0 |
Погрешности прямых измерений: $$ Delta_l=2 text=0,2 text, Delta_F=0,05 text $$ Найдем моменты сил и погрешности вычислений: begin M_1=F_1cdot l_1=2,9cdot 5=14,5 (textcdot text)\[7pt] delta_=frac+frac=frac+fracapprox 0,04+0,017=0,057=5,7text \[7pt] Delta_=M_1cdot delta_=14,5cdot 0,057approx 0,8 (textcdot text)\[7pt] M_1=(14,5pm 0,8) textcdot text\[7pt] \[7pt] M_2=F_2cdot l_2=1,0cdot 15=15,0 (textcdot text)\[7pt] delta_=frac+frac=frac+fracapprox 0,013+0,05=0,063=6,3 text \[7pt] Delta_=M_2cdot delta_=15,0cdot 0,063approx 0,9 (textcdot text)\[7pt] M_2=(15,0pm 0,9) textcdot text end Таким образом, с учетом вычисленных погрешностей: $$ M_1=M_2 $$
Погрешность вычислений для (frac) begin delta_=frac+frac=frac+fracapprox 0,04+0,013=0,053=5,3text\[7pt] Delta_=fraccdot delta_=3,0cdot 0,053approx 0,2\[7pt] frac=3,0pm 0,2 end Таким образом, с учетом вычисленных погрешностей: $$ frac=frac $$
Выводы
На основании проделанной работы можно сделать следующие выводы.
Моменты сил, приложенных слева и справа от оси вращения рычага, равны $$ M_1=(14,5pm 0,8) textcdot text, M_2=(15,0pm 0,9) textcdot text $$ Таким образом, с учетом вычисленных погрешностей, (M_1=M_2) — правило моментов выполняется.
Отношения сил и плечей равны begin frac=2,9pm 0,2, frac=3,0pm 0,2 end
Таким образом, с учетом вычисленных погрешностей (frac=frac) — правило отношений выполняется.
Эксперименты подтвердили условие равновесия рычага.
🔍 Видео
Система сходящихся сил. Решение задач по МещерскомуСкачать

Определение реакций опор простой рамыСкачать

Определение опорных реакций балки. Сопромат для чайников ;)Скачать

Теоретическая механика. Нахождение реакций связей на при плоской системе сил. Задача 1, часть 1Скачать

4.2 Проекция силы на ось координатСкачать

Задача №1 Система сходящихся силСкачать

определение реакций в стержнях от действия грузовСкачать

Момент силыСкачать

Видеоурок 2. Определение реакций двухопорных балок.Скачать

Урок 77. Решение задач статики (часть 1)Скачать

Видеоурок 1. Определение реакций жёстких стержней.Скачать

Условия равновесияСкачать

Урок 1. Условия равновесия твердого тела. Теория. ЕГЭСкачать

Урок 81 (осн). Задачи на правило моментовСкачать