Какое из приведенных уравнений соответствует рисунку i2 i3 i4 i1

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

При последовательном соединении двух конденсаторов, подключенных к источнику питания, один из них оказался пробитым. Как изменится запас прочности другого конденсатора?

Длину и диаметр проводника увеличили в два раза. Как изменится сопротивление в проводнике?

-не изменится;
+ уменьшится в два раза;
— увеличится в два раза;

Как изменится проводимость проводника при увеличении площади его поперечного сечения S?

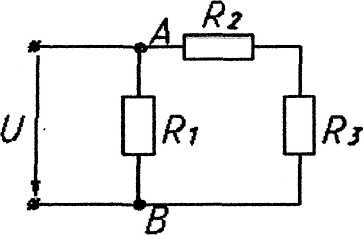
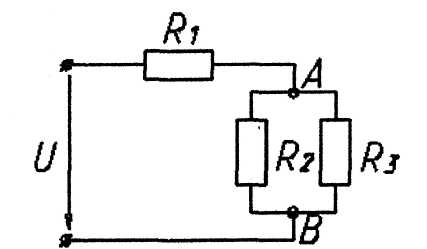
В приведенной схеме сопротивление R3 увеличилось?

Как изменится напряжение на других участках цепи, если напряжение U считать постоянным?

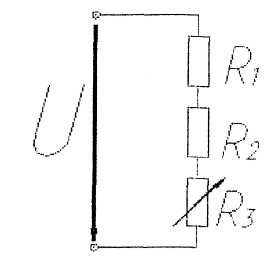
-не изменится;
+ уменьшится;
— увеличится;

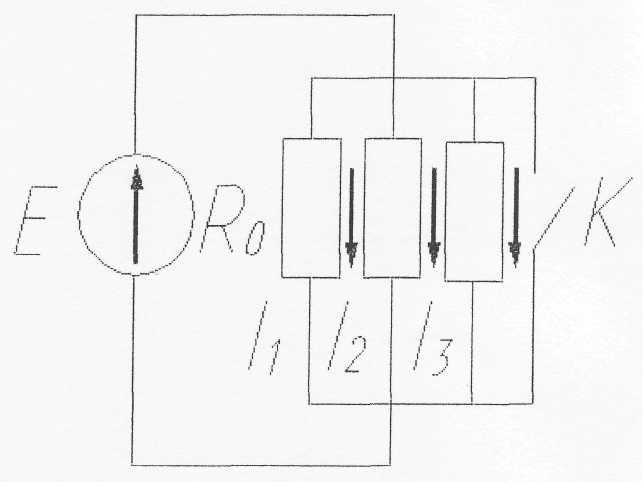
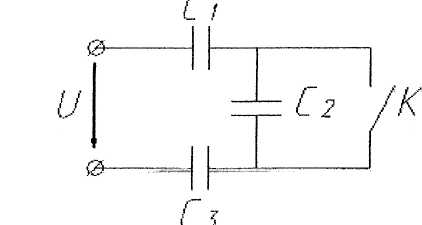
4. Как изменится напряжение на участках R2 и R3 при замыкании ключа К (U=const)?

+ увеличится;

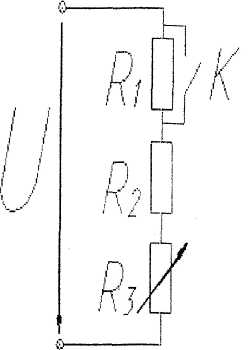
5. Каким должно быть сопротивление амперметра R_a, чтобы он не влиял на режим работы цепи?

-Rа больше R₁+R₂;

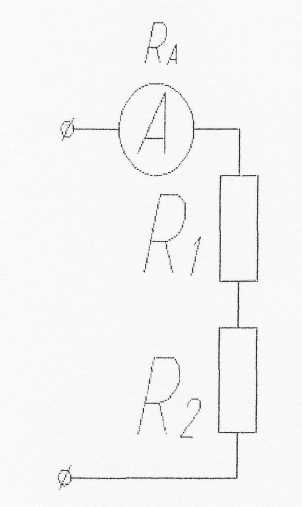
-Ra примерно равно Rl+R2;

6. Как изменятся токи I₁; I₂; I₃ при замыкании ключа?

+ станут равны нулю.

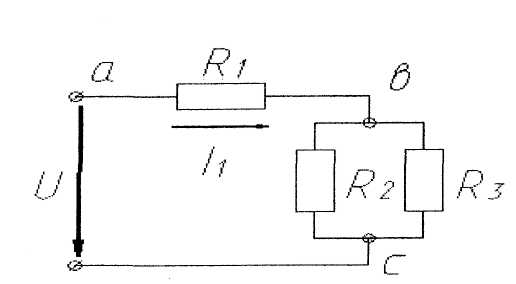
7. Какое соединение представлено на схеме?

8.Как изменится напряжение на участке АВ, если параллельно ему включить еще одно сопротивление (U=const)?

-не изменится;
+ уменьшится;

9. Можно ли считать, что сопротивления R₁ и R₂ соединены параллельно?

Можно ли считать, что сопротивления R2 и R4 включены последовательно?

— можно;

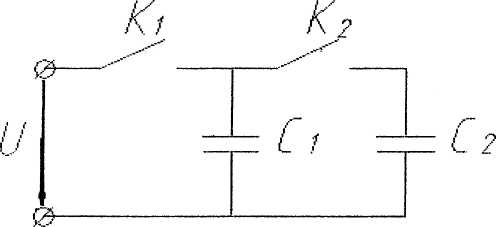
При каком положении ключей К, и эквивалентное сопротивление цепи будет минимальным?

+ ключ К1 замкнут, ключ К2 замкну;

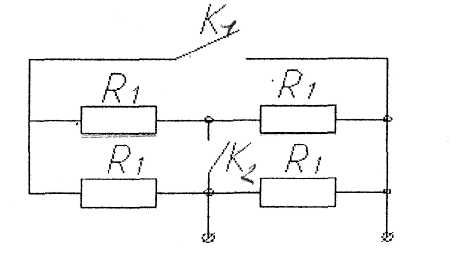
— ключ К1 разомкнут, ключ К2 разомкнут;

— ключ К1 замкнут, ключ К2 разомкнут;

— ключ К1 разомкнут, ключ К2 замкнут.

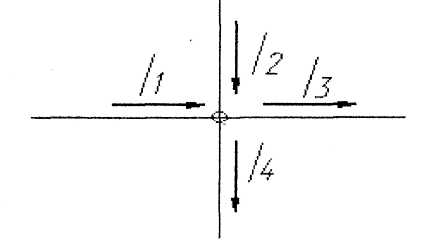
Какое из приведенных уравнений соответствует рисунку?

— I₁+ I ₂ = I ₃ + I ₄;

13. Является ли движение электрона вокруг ядра электрическим током?

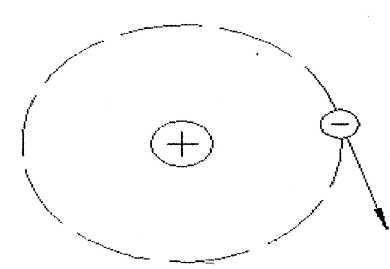
Какой из приведенных графиков является графиком постоянного тока?

— правый;

За 1 час при постоянном токе был перенесен заряд в 180 Кл. Определить силу тока?

Можно ли, пользуясь графиком постоянного тока, определить какое количество электричества прошло за проводник за данное время?

17. В результате изменения сопротивления нагрузки ток в цепи увеличился. Как это будет влиять на напряжение на зажимах цепи?

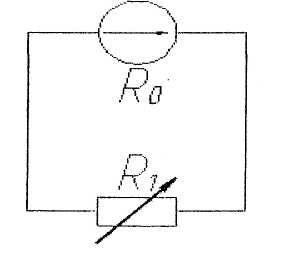
-напряжение U будет расти;

+ напряжение U будет уменьшаться;

-напряжение U будет неизменным;

В каком положении ключа К показания вольтметра будет больше?

+ в разомкнутом;

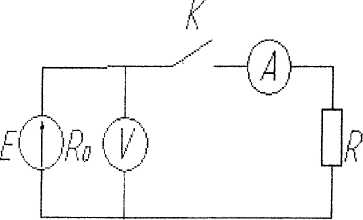
— напряжение не зависит от положения ключа.

Какая из приведенных формул для определения тока I верна?

20. В данной схеме C1»C2, Какой из этих емкостей можно пренебречь при приближенном определении общей емкости?

21.В данной схеме C1»C2. Какой из этих емкостей можно пренебречь при приближенном определении общей емкости?

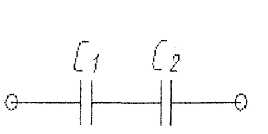
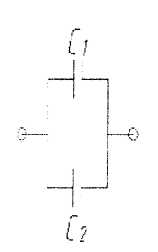
Для правильного регулирования емкости используются конденсаторы переменной емкости Си?

Пусть С1 = 100пФ, Сп=10-500 пФ.

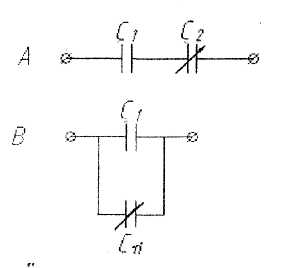
В какой из приведенных схем общая емкость меняется в более широких пределах?

-в обеих схемах пределы изменяются одинаково;

-в схеме В;
+ в схеме А:

Конденсатор переменной емкости состоящий из группы неподвижных А и подвижных пластин В, которые поворачиваются относительно неподвижных . Какое соединение представляет собой схема конденсатора?

-последовательное;
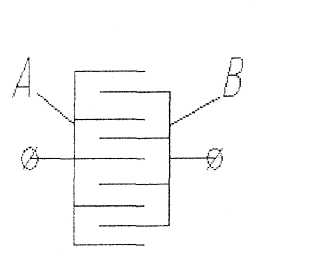
+ параллельное;

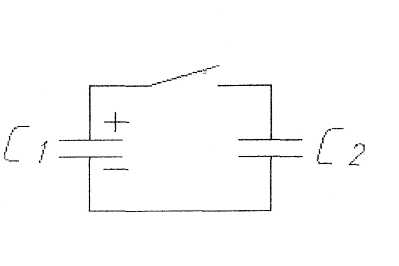
Конденсатор С1, заряжен до напряжения U1, замыкают на разряженный конденсатор С2. Как изменится энергия батареи конденсаторов после заряда конденсатора С2?

— не изменится;

При параллельном соединении трех конденсаторов, подключенных к источнику питания, один из них (С3) оказался пробитым. Как изменится напряжение на конденсаторах и какой станет их обща емкость?

— U = const; С обш = С1+С2

— U — 0; С общ = С1+ С2
+ U — 0; С общ = 0;

— U = 0; С общ = бесконечности

26.Три конденсатора, подключенные к источнику питания соединены последовательно. С1>С2>С3. Как будет распределяться напряжение на конденсаторах?

При последовательном соединении двух конденсаторов, подключенных к источнику питания, один из них оказался пробитым. Как изменится запас прочности другого конденсатора?

28.Как изменится величина энергии последовательно включенных конденсаторов и их заряд при замыкании ключа К?

— энергия увеличится, заряд уменьшится.

— энергия увеличится, заряд не изменится.

— энергия увеличится, заряд увеличится.

+ энергия уменьшится, заряд не изменится.

29. При разомкнутом ключе К2 замыкающий ключ K1 и конденсатор C1 заряжаются до напряжения U. Затем ключ K1 размыкают, а К2 замыкают. Как изменится напряжение на конденсаторах C1 и С2 и общий заряд, если ёмкость C1 > С2?

+ U1=U2

Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Какое из приведенных уравнений соответствует рисунку?

Число узловых уравнений в системе при расчете электрических цепей методом уравнений Кирхгофа должно быть (q – число узлов в схеме):

Число контурных уравнений в системе при расчете электрических цепей методом уравнений Кирхгофа должно быть (Р – число ветвей в схеме; Р_Т – число ветвей с источником тока; q – число узлов):

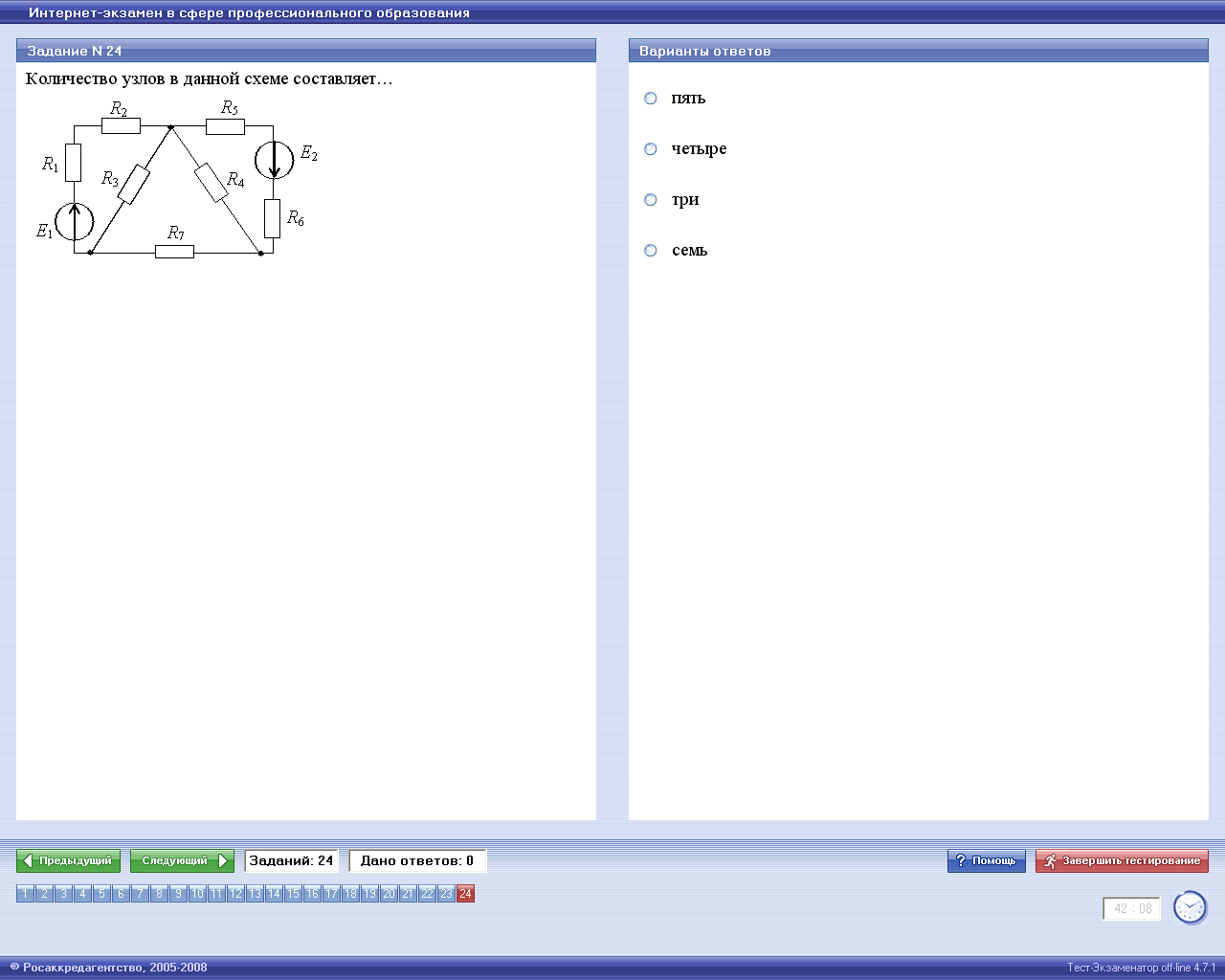
Количество узлов в данной схеме составляет…

Если сопротивления R₁=100 Ом, R₂=20 Ом, R₃=200 Ом, то в ветвях будут наблюдаться следующие токи…

Полярность на вольтметре показывает направление напряжения. Если показание вольтметра pV=50 В, то показание амперметра pA равно…

Эквивалентное сопротивление цепи относительно источника ЭДС составит…

Закон Ома графически выражается в виде ###

+: прямой, проходящей через начало координат

Определить эквивалентное сопротивление цепи, если: R₁ = 10 Ом, R₂ = R₃ = 5 Ом, R₄ = R₅=10

При увеличении числа параллельных ветвей в цепи постоянного тока эквивалентная проводимость:

Определить показание вольтметра, если U = 50В, R₁=R₂ =20 Ом

Найти эквивалентную проводимость цепи, если R₁ = 4 Ом, R₂ = 2 Ом, R₃ = 3 Ом

Определить показание амперметра, если U = 50В, R₁=R₂ =20 Ом

Определить показание амперметра, если U = 50В, R₁=R₂ =20 Ом

Согласно закону Ома:

+:

Определить сопротивления R₁ и R₂, если известно: R₁= R₂, U=50В, I = 1 А:

Определить ток в цепи если известно: R₁= R₂= 20 Ом, R₃=30 Ом, U=70В:

Определить показание вольтметра, если I₁ = 4 А, R₁=R₂ =20 Ом

Определить эквивалентное сопротивление цепи, если R₁ = R₂ = R₃ = R₄ = 1 Ом

Если сопротивления всех резисторов R одинаковы и равны 6 Ом, то входное сопротивление схемы, изображенной на рисунке, равно ###

Если сопротивления всех резисторов одинаковый равны по 6 Ом, то эквивалентное сопротивление пассивной резистивной цепи, изображенной на рисунке, равно ###

Если сопротивления R₁=100 Ом, R₂=20 Ом, R₃=200 Ом, то на резисторах будут наблюдаться следующие напряжения ###

Эквивалентное сопротивление цепи относительно источника ЭДС составит ###

Эквивалентное сопротивление участка цепи, состоящего из трех последовательно соединенных сопротивлений номиналом 1 Ом, 10 Ом, 1000 Ом, равно ###

Если напряжения на трех последовательно соединенных резисторах относятся как 1:2:4, то отношение сопротивлений резисторов ###

+: подобно отношению напряжений 1:2:4

Если номинальный ток I = 100 А, тогда номинальное напряжение U источника напряжения с ЭДС Е = 230 В и внутренним сопротивлением R_ВТ = 0,1 Ом равно ###

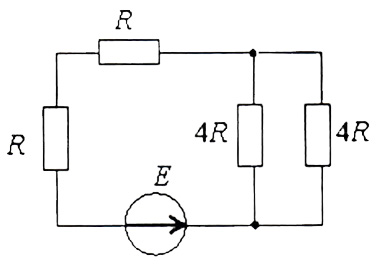
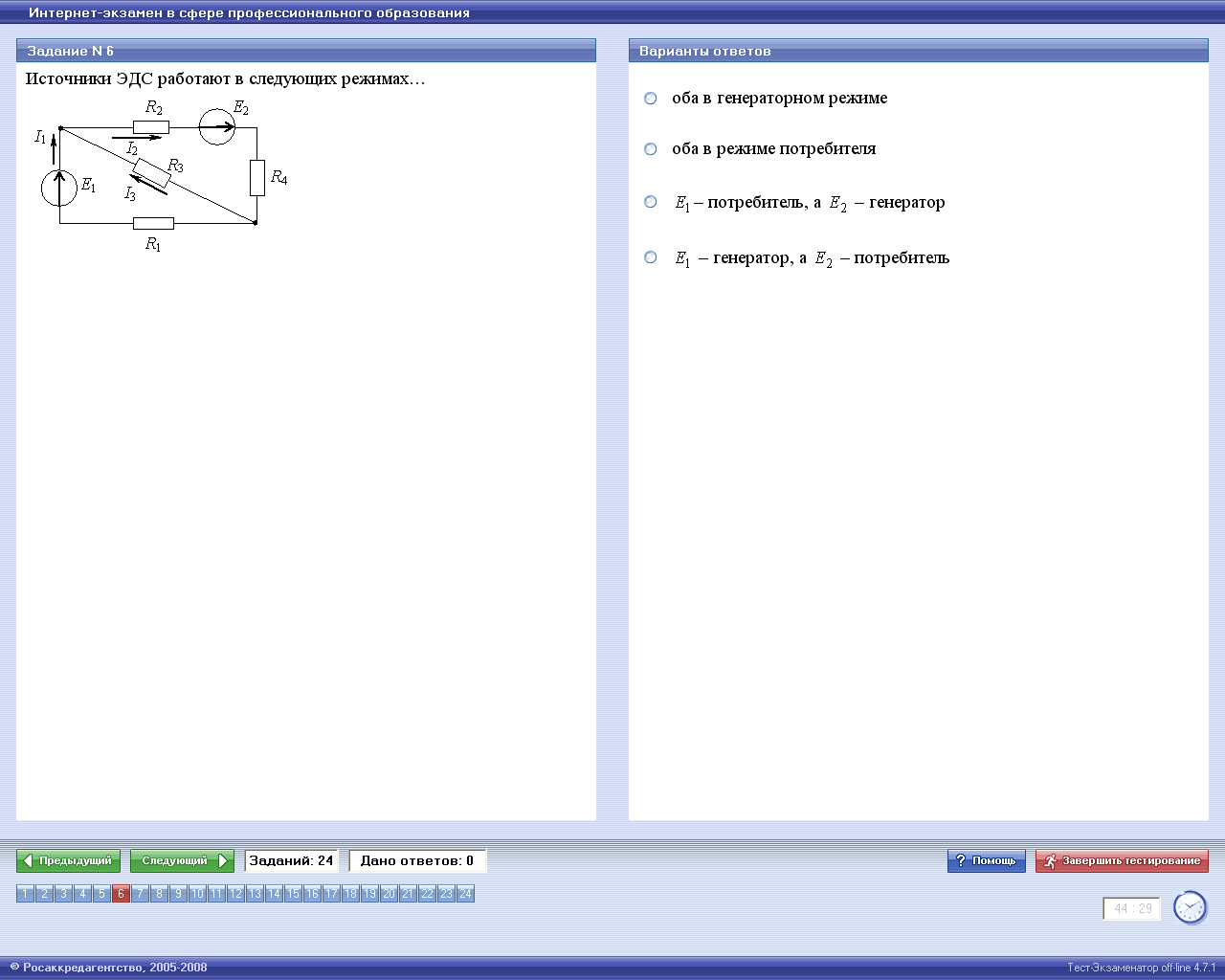
Источники ЭДС работают в следующих режимах…

+: оба в генераторном режиме

Уравнение баланса мощностей представлено выражением…

Если сопротивления цепи заданы в Омах, а токи в ветвях составляют I₁=1 А, I₂=2 А, I₃=1 А, то потребляемая мощность имеет величину…

При известных величинах токов и сопротивлений, потребляемая мощность составит…

Выражение для мощности P₀, выражающейся на внутреннем сопротивлении источника R₀ имеет вид…

+:

Мощность источника питания определяется формулой:

+:

В цепи известны сопротивления резисторов R₁=20 Ом, R₂=30 Ом, ЭДС источника E=120 B и мощность Р=120 Вт всей цепи. Мощность Р₂ второго резистора будет равна ###

Выражение для мощности Р, выделяющейся в нагрузке с сопротивлением R, имеет вид ###

Эквивалентное сопротивление цепи будет равно:

Если пять резисторов с сопротивлениями R₁ = 100 Ом, R₂ = 10 Ом, R₃ = 20 Ом, R₄ = 500 Ом, R₅ = 100 Ом соединены последовательно, то ток будет ###

В цепи известны сопротивления R₁ = 30 Ом, R₂ = 60 Ом, R₃ = 120 Ом и ток в первой ветви I₁ = 4 А. Тогда ток I и мощность Р цепи соответственно равны ###

Видео:Решение задачи. Расчет электрической цепи по законам КирхгофаСкачать

Правила (законы) Кирхгофа простыми словами

На практике часто встречаются задачи по расчётам параметров токов и напряжений в различных разветвлённых цепях. В качестве инструмента для расчётов используют правила Кирхгофа (в некоторой литературе их называют еще законами, хотя это не совсем корректно) – одни из фундаментальных правил, которые совместно с законами Ома позволяет определять параметры независимых контуров в самых сложных цепях.

Учёный Густав Киргхоф сформулировал два правила [1], для понимания которых введено понятие узла, ветви, контура. В нашей ситуации ветвью будем называть участок, по которому протекает один и тот же ток. Точки соединения ветвей образуют узлы. Ветви вместе с узлами образуют контуры – замкнутые пути, по которым течёт ток.

Видео:Расчет электрической цепи постоянного тока методом узловых и контурных уравненийСкачать

Первое правило Кирхгофа

Первое правило Густава Кирхгофа сформулировано исходя из закона сохранения заряда. Физик понимал, что заряд не может задерживаться в узле, а распределяется по ветвям контура, образующим это соединение.

Кирхгоф предположил, а впоследствии обосновал на основании экспериментов, что количество зарядов зашедших в узел такое же, как и количество тока вытекающего из него.

На рисунке 1 изображена простая схема, состоящая из контуров. Точками A, B, C, D обозначены узлы контура в центре схемы.

Рис. 1. Схема контура

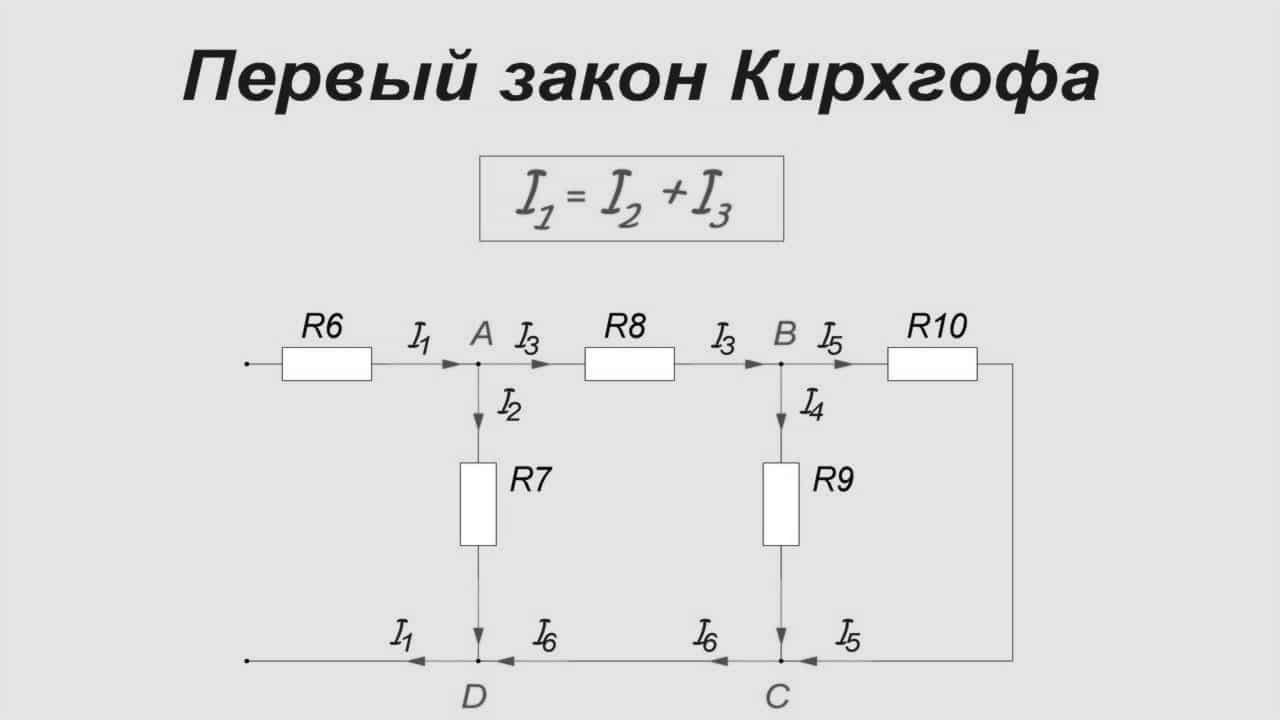
Ток I₁ входит в узел A, образованный ветвями контура. На схеме электрический заряд распределяется в двух направлениях – по ветвям AB и AD. Согласно правилу Кирхгофа, входящий ток равен сумме выходящих: I₁ = I₂ + I₃.

На рисунке 2 представлен абстрактный узел, по ветвям которого течёт ток в разных направлениях. Если сложить векторы i₁, i₂, i₃, i₄ то, согласно первому правилу Кирхгофа, векторная сумма будет равняться 0: i₁ + i₂ + i₃ + i₄ = 0. Ветвей может быть сколько угодно много, но равенство всегда будет справедливым, с учётом направления векторов.

Запишем наши выводы в алгебраической форме, для общего случая:

Для использования этой формулы, требуется учитывать знаки. Для этого необходимо выбрать направление одного из векторов тока (не важно, какого) и обозначить его знаком «плюс». При этом знаки всех других величин определить, исходя от их направления, по отношению к выбранному вектору.

Чтобы избежать путаницы, ток, направленный в точку узла, принято считать положительным, а векторы, направленные от узла – отрицательными.

Изложим первое правило Кирхгофа, выраженное приведённой выше формулой: «Алгебраическая сумма сходящихся в определённом узле токов, равна нулю, если считать входящие токи положительными, а отходящими – отрицательными».

Первое правило дополняет второе правило, сформулированное Кирхгофом. Перейдём к его рассмотрению.

Видео:Как составить уравнения по законам Кирхгофа?Скачать

Второе правило Киргхофа

Из третьего уравнения Максвелла вытекает правило Кирхгофа для напряжений. Его ещё называют вторым законом.

Это правило гласит, что в замкнутом контуре, на резистивных элементах, алгебраическая сумма напряжений (включая внутренние), равна сумме ЭДС, присутствующих в этом же замкнутом контуре.

При этом токи и ЭДС, векторы которых совпадают с направлением (выбирается произвольно) обхода контура, считаются положительными, а встречные к обходу токи – отрицательными.

Рис. 4. Иллюстрация второго правила Кирхгофа

Формулы, которые изображены на рисунке применяются в частных случаях для вычисления параметров простых схем.

Формулировки уравнений общего характера:

, где где L_k и C_k – это индуктивности и ёмкости, соответственно.

Линейные уравнения справедливы как для линейных, так и для нелинейных линеаризованных цепей. Они применяются при любом характере временных изменений токов и напряжений, для разных источников ЭДС. При этом законы Кирхгофа справедливы и для магнитных цепей. Это позволяет выполнять вычисления для поиска соответствующие параметров.

Видео:Метод контурных токов - определение токов. ЭлектротехникаСкачать

Закон Кирхгофа для магнитной цепи

Применение независимых уравнений возможно и при расчётах магнитных цепей. Сформулированные выше правила Кирхгофа справедливы и для вычисления параметров магнитных потоков и намагничивающих сил.

То есть, для магнитных потоков первое правило Кирхгофа можно выразить словами: «Алгебраическая сумма всевозможных магнитных потоков относительно узла магнитной цепи равняется нулю.

Сформулируем второе правило для намагничивающих сил F: «В замкнутом магнитном контуре алгебраическая сумма намагничивающих сил приравнивается к сумме магнитных напряжений». Данное утверждение выражается формулой: ∑F=∑U или ∑Iω = ∑НL, где ω – количество витков, H – напряжённость магнитного поля, символ L обозначает длину средней линии магнитопровода. ( Условно принимается, что каждая точка этой линии совпадает с линиями магнитной индукции).

Второе правило, применяемое для вычисления магнитных цепей, есть не что иное, как альтернативная форма представления закона полного тока.

Примечание: Составляя уравнения с использованием формул, вытекающих из правил Кирхгофа, надо прежде определиться с положительным направлением потоков, функционирующих в ветвях, сопоставив их с направлением обходов существующих контуров.

При совпадении векторов магнитного потока с направлениями обхода (на некоторых участках), падение напряжения на этих ветвях берём со знаком « + », а встречные ему – со знаком « – ».

Видео:Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать

Примеры расчета цепей

Рассмотрим ещё раз рисунок 3. На нём изображено 4 разнонаправленных вектора: i₁, i₂, i₃, i₄. Из них – два входящие ( i₂, i₃) и два исходящие из узла (i₁, i₄). Положительными будем считать те векторы, которые направлены в точку соединения ветвей, а остальные – отрицательными.

Тогда, по формуле Кирхгофа, составим уравнение и запишем его в следующем виде: – i₁ + i₂ + i₃ – i₄ = 0.

На практике такие узлы являются частью контуров, обходя которые можно составить ещё несколько линейных уравнений с этими же неизвестными. Количество уравнений всегда достаточно для решения задачи.

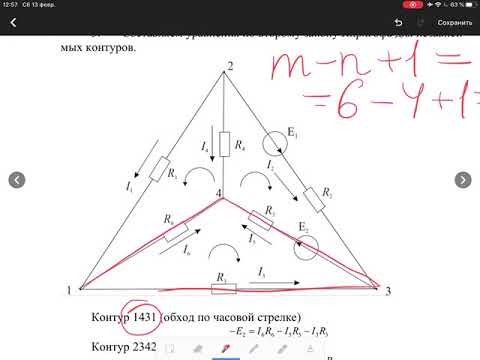
Рассмотрим алгоритм решения на примере рис. 5.

Рис. 5. Пример для расчёта

Схема содержит 3 ветви и два узла, которые образуют три пары по два независимых контура:

Запишем независимое уравнение, выполняющееся, например, в точке а. Из первого правила Кирхгофа вытекает: I₁ + I₂ – I₃ = 0.

Воспользуемся вторым правилом Кирхгофа. Для составления уравнений можно выбрать любой из контуров, но нам необходимы контуры с узлом а, так как для него мы уже составили уравнение. Это будут контуры 1 и 2.

Пишем уравнения:

Решаем систему уравнений:

Так как значения R и E известны (см. рисунок 5), мы придём к системе уравнений:

Решая эту систему, получим:

Потенциал узла а равен: U_a = I₃*R₃ = 3,55 × 3 = 10,65 В. Чтобы убедиться в верности наших расчётов, проверим выполнение второго правила по отношению к контуру 3:

E₁ – E₂ + I₁R₁+ I₂R₂ = 12 – 15 + 1,36 – 4,38 = – 0,02 ≈ 0 (с учётом погрешностей, связанных с округлениями чисел при вычислениях).

Если проверка выполнения второго правила успешно завершена, то расчёты сделаны правильно, а полученные данные являются достоверными.

Применяя правила (законы) Кирхгофа можно вычислять параметры электрической энергии для магнитных цепей.

📽️ Видео

8 класс, 21 урок, Расчет электрических цепейСкачать

Лекция 020-1. Цепи постоянного тока. Расчет при помощи уравнений КирхгофаСкачать

РЕАКЦИИ ИОННОГО ОБМЕНА, ИОННОЕ УРАВНЕНИЕ - Урок Химия 9 класс / Подготовка к ЕГЭ по ХимииСкачать

Правила Кирхгофа: пример расчёта цепи с источниками токаСкачать

Законы Кирхгофа. Метод контурных уравненийСкачать

7 класс, 35 урок, Графическое решение уравненийСкачать

Метод узловых и контурных уравненийСкачать

Лекция по электротехнике 2.5 - Составление уравнений КирхгофаСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

021 Расчет электрической цепи по законам КирхгофаСкачать

Разветвленные цепи. Правила КирхгофаСкачать