Какое из представленных уравнений есть уравнение производственной функции кобба дугласа

Производственная функция — экономико-математическая количественная зависимость между величиной выпуска (объемом продукции фирмы) и факторами производства, такими как затраты ресурсов, уровень технологий.

Наиболее известные примеры производственных функций: функция Кобба-Дугласа вида $Y=Acdot L^cdot K^$, в которой предполагается постоянные эластичности ($alpha$ и $beta$) выпуска по факторам производства $K$ и $L$ соответственно (капитал и трудовые затраты); линейная производственная функция: $Y=aK+bL$, функция Леонтьева и т.д.

В этом разделе вы найдете подробно решенные задачи, касающиеся производственной функции (в том числе модели Кобба-Дугласа).

Видео:Анализ производственной функции Кобба-ДугласаСкачать

Производственная функция: задачи с решениями

Задача 1. Производственная функция коммерческого предприятия имеет вид $f=10sqrtcdot sqrt$, где $f$ — товарооборот, тыс. руб.; $x_1$ — производственная площадь, м ; $x_2$ — численность работников, сотни человек. Рассмотрите изокванту уровня $y_0$ и найдите точку $C_1$ и точку $C_2$. Сделайте вывод о возможности замены ресурсов. Полученные результаты изобразите графически.

Задача 2. Исходные данные. Фирма, производящая продукцию при заданной рынком системе цен по технологии, отображающейся производственной функцией $Q = 20 L^$, может продавать любой объем своей продукции по цене Р = 6. Фирма может использовать любое количество труда по цене w = 40.
1. Какой тип производственной функции представлен в задании? В чем ее особенность? Приведите пример подобного производства. Изобразите график заданной производственной функции, а также графики среднего и предельного продуктов переменного фактора (труда).
2. На основе представленных данных выведите функции общих, средних и предельных затрат фирмы, функцию индивидуального предложения фирмы и определите объем предложения при заданной цене блага.
3. Дайте характеристику статуса фирмы на товарном и факторном рынках в представленном примере. Раскройте различия в поведении фирмы-совершенного конкурента и фирмы-монопсониста на рынке фактора. Приведите примеры подобного поведения фирм на рынке труда.
4. Выведите функцию спроса фирмы на труд, если цена блага P = 6 и остается неизменной. Определите объем спроса на труд при w = 40. Решение сопроводите графиком. Укажите несколько факторов (не менее трех), влияющих на спрос фирмы на труд.

Задача 3. Процесс производства некоторого товара описывается с помощью производственной функции $q=f(x_1, x_2)=54x_1^x_2^$. Для плана (2,5) найти первый второй предельные продукты. Дайте экономическую интерпретацию полученным результатам. Выясните, характеризуется ли ПФ той или иной разновидностью эффекта масштаба. Предполагая, что производитель приобретает ресурсы по ценам (2,7) найдите функцию переменных издержек $C_v(q)$.

Видео:Теория потребителя. Функция Кобба-ДугласаСкачать

Модель Кобба-Дугласа: задачи с решениями

Задача 4. Производственная функция фирмы имеет вид: $Q = К^cdot L^$. Предположим, что в день затрачивается 4 часа труда (L = 4) и 4 часа работы машин (К = 4).
Определить:
1) максимальное количество выпускаемой продукции;
2) средний продукт труда;
3) допустим, что фирма увеличила затраты обоих факторов в два раза. Каков будет объем выпускаемой продукции?

Задача 5. Задана производственная функция Кобба-Дугласа
Изобразить изокванту, соответствующую плану (36,27). Какое количество продукта выпускается при этом плане?
Найти первый, второй предельные продукты для плана (36,27) и дать экономическую интерпретацию полученным результатам.
Каким эффектом от расширения масштабов производства характеризуется производственная функция
Каковы затраты производителя на покупку ресурсов при плане производства (36,27) и заданном векторе цен на ресурсы (3,4)?
Найти самый дешевый (оптимальный) план по ресурсам, обеспечивающий выпуск такого же количества продукции, что и для плана (36,27). Найти аналитически решение этой задачи
методом Лагранжа
методом подстановки.
Сделать геометрическую иллюстрацию решения задачи, изобразив ОДР и целевую функцию линиями уровня.

Задача 6. На основании представленных в таблице ниже данных построить ПФ типа Кобба-Дугласа. Сделать прогноз объема производства отрасли на 2000 год, если планируются увеличение основных фондов на 20% и одновременное уменьшение трудовых ресурсов на 5% относительно предыдущего года. Пусть заданы агрегированные основные показатели некоторой отрасли за четыре года:

Задача 7. Для построенной в самостоятельной работе производственной функции рассчитать предельные производительности, предельные нормы замещения ресурсов в 1993 и 1999 годах, сделать сравнительный экономический анализ. При расчетах предположить, что ресурсы в исследуемом году заданы, объем производства вычисляется.

Задача 8. Пусть производственная функция имеет вид $Y = 0.94 cdot K^cdot L^$. Для базового года $K_0 = 727$ млн ден. ед., $L_0 = 97.7$ тыс. человек. Для отчётного года $K_1 = 977$ млн ден. ед., $L_1 = 127.7$ тыс. человек. Подсчитать индексы изменения характеристик, масштаб и экономическую эффективность производства. Дать экономическую интерпретацию.

Задача 9. Производственная функция фирмы, выпускающая линолеум, имеет вид $Y=177 K^ L^$. Здесь $Y$ – сотни м*м, $K$ – тыс. ден. ед., $L$ – сотня рабочих (сот. р.).
Стоимость ресурсов W=5,13 тыс. ден. ед./сот. раб.
q = 10 тыс. ден. ед./тыс. ден. ед.
Издержки производства ограничены суммой C = 1770 тыс. ден. ед.
Найти максимальный выпуск продукции, оптимальное количество рабочих и стоимость капитальных фондов.
Построить график изокванты и изокосты. Отметить оптимальную точку.
Оценить, как изменится выпуск продукции, если:
а) увеличить заработную плату на 8%;
б) уменьшить цену на фонды в два раза;
в) ввести дополнительные инвестиции в производство в количестве 57,7 тыс. ден. ед.

Задача 10. Найти объем продукции, произведенной за период $[0;52]$, если функция Кобба-Дугласа имеет вид: $f(t)=(364+7t)e ^$

Задача 11. 1. Выпуск продукции фирмой описывается функцией Кобба-Дугласа $Y=AK^L^$. Ставка заработной платы равна $p_L$, норма процента на используемый капитал — $p_K$.
2. По заданному уровню выпуска продукции $Y$ определить объемы факторов $K$ и $L$, при которых общие издержки будут минимальны, и величину этих издержек.
3. По известной величине общих издержек $TC$ определить объем факторов $K$ и $L$, обеспечивающие максимальный выпуск продукции, и соответствующий объем выпуска.

Задача 12. На основании следующих данных построить производственную функцию Кобба-Дугласа.
Здесь $Y_i$ — производственный национальный доход (млрд. руб.), $K_i$ — среднегодовые основные производственные фонды (млрд. руб.), $L_i$ — среднегодовая численность занятых в материальном производстве (млн. чел.). Имеется прогноз на 1997 год: основных производственных фондов $K_cdot N$ млн. руб. и трудовых ресурсов $L_cdot N$, где $N$ (номер) млн. чел. На основании полученной производственной функции сделать точечный прогноз национального дохода на 1997 год.

Задача 13. Производственная функция задается формулой $Q = 150 K^L^$, где Q — выпуск, K – капитал, L — труд.
Найти:
a) Предельные продукты труда и капитала при K=16, L=125.
б) Коэффициенты эластичности выпуска по труду и капиталу и объяснить их экономический смысл для полученных значений.

Видео:Построение производственной функции Кобба-ДугласаСкачать

Производственная функция Кобба-Дугласа

Под производством в экономике понимают применение ресурсов и технологий для того, чтобы получить продукт, который можно было бы продать. Это процесс, в результате которого создается товар или предоставляется услуга, обладающая полезностью для покупателя. Спрос и предложение на рынке определяют их цену. Количество выпущенного товара, а в конечном счете и его стоимость, показывают производство и производственная функция. На спрос влияют ценовые и другие факторы. К последним относят доходы потребителей, их вкусы, стоимость товаров-субститутов.

Экономическое благосостояние создается в процессе производства. Это означает, что любая хозяйственная деятельность прямо или косвенно направлена на удовлетворение человеческих потребностей. От последнего как раз и зависит экономическое благосостояние государства. Чем больше степень удовлетворения потребностей и доля среднего класса в населении, тем выше национальное развитие. Производственная функция объясняет это улучшение благосостояния людей в процессе выпуска продукции.

Видео:Микра для начинающих/Основы теории производства.Функция Кобба-ДугласаСкачать

Общие сведения

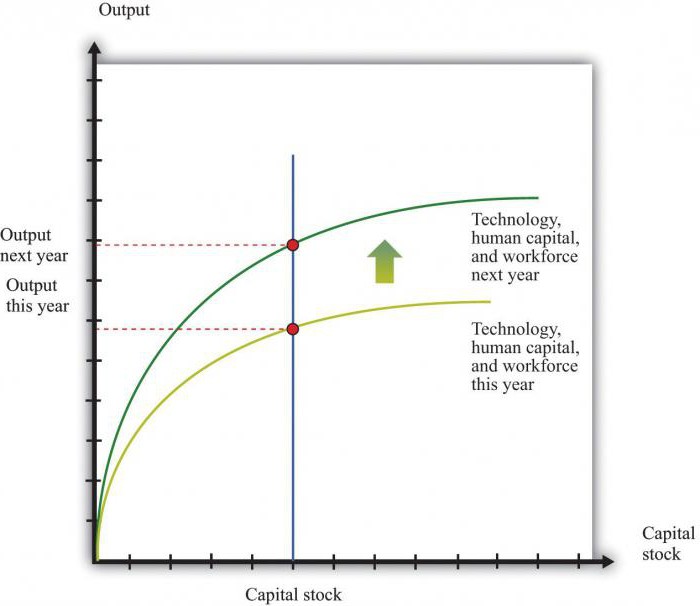
Производственная функция в экономике соотносит фактический выпуск с ресурсами, которые были вложены в процессе для его получения. Данное понятие является ключевым в неоклассических теориях. Производственная функция используется для того, чтобы определить маржинальный продукт и общую эффективность. Последняя является краеугольным камнем всех экономических исследований. Первостепенная задача, которую решает производственная функция, это определение эффективности использования факторов производства и распределение полученных доходов между ними без учета технологических проблем, которые могут возникнуть.

В макроэкономике агрегированные показатели рассчитываются для того, чтобы понять, как происходит экономический рост: в частности, благодаря аккумуляции капитала или совершенствованию технологии. Следует отметить, что есть ученые, отвергающие концепцию агрегированной производственной функции, но эта точка зрения не является распространенной.

Видео:Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Теория производственных функций

В строгом смысле выпуск продукции нельзя представить математически как сумму или произведение вложенных ресурсов. Поскольку каждый из наборов факторов производства можно использовать для создания целого ряда товаров. Для того чтобы соответствовать математическому определению, делается предположение, что производственная функция отображает максимально возможный выпуск товаров из данного набора ресурсов. Таким образом, она обозначает минимальное соотношение факторов, которое необходимо для создания оговоренного количества продукции. Предположение о максимально возможном выпуске позволяет экономистам абстрагировать от технологических и управленческих проблем и сфокусировать свое внимание исключительно на проблеме совокупной эффективности. Ее решение позволяет разобраться, до какой степени один ресурс может быть заменен другим. Производственная функция фирмы не отображает монетарную зависимость между выпуском и задействованными факторами, хотя и включает физические объемы. Цена продукции и стоимость факторов остаются за кадром.

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Виды производственных функций

Экономико-математическия модели, которые характеризуют зависимость выпуска от различных факторов и национального хозяйства в целом, могут учитывать следующие показатели: объем произведенной продукции (в стоимостном или натуральном выражении), затраченный основной капитал и фонды, вложенные трудовые ресурсы, расход электроэнергии, количество станков и оборудования. Выделяют три группы производственных функций:

1. Однофакторные. К этой группе относят линейную, параболическую, степенную и показательную функцию.
2. Двухфакторные. К этой группе относят функции Леонтьева, Кобба-Дугласа, Аллена, Солоу, линейную, с постоянной эластичностью замены используемых ресурсов.
3. Многофакторные.

Функция Леонтьева используется для моделирования полностью автоматизированных или мелкомасштабных процессов. Она не допускает отклонения от строго детерминированных технологических норм ресурсов на единицу выпуска. Функция Кобба-Дугласа описывает среднемасштабные процессы (от промышленного объединения до целой отрасли). Главное условие ее использования – стабильное и относительно устойчивое их функционирования. Функция Аллена описывает мелкомасштабные процессы, в которых ограничены возможности переработки ресурсов. Она предназначена для ситуаций, когда чрезмерный рост каждого из факторов оказывает отрицательное воздействие на выпуск. Функция Солоу рекомендуется к использованию в случае моделирования систем любого масштаба. Основное условие ее использования – зависимость нормы замещения от пропорций ресурсов.

Видео:21 функция полезности Кобба Дугласа и квазилинейная функция полезностиСкачать

Функция Кобба-Дугласа в экономике

Двумя основными факторами производства являются труд и капитал. Их соединение в определенной пропорции позволяет создать продукт. Производственная функция Кобба-Дугласа отражает технологическое соотношение между объемом труда и капитала для выпуска некоторого количества товара. Данная модель является двухфакторной и была проверена статистически двумя учеными, по фамилиям которых она и была названа, в 1927-1947 годах. Иногда термин «производственная функция Кобба-Дугласа» имеет более узкое значение, указывая на постоянную отдачу от масштаба (в этом случае b=1-a в основной формуле).

Видео:Проверка адекватности производственной функции Кобба-ДугласаСкачать

Основная формула

Производственная функция Дугласа-Кобба отражает зависимость выпуска определенного товара от соотношения двух факторов: труда и капитала. В наиболее общем виде формула выглядит следующим образом: Y=A*L b *K a , где буквами обозначены следующие показатели:

• Y – общий объем производства (реальная стоимость всех товаров, выпущенных в этом году);
• L – вклад труда (количество человеко-часов, отработанных за данный период);
• K –объем затраченного капитала (реальная стоимость машин, оборудования и зданий);
• A – общая продуктивность факторов;
• a и b – эластичность труда и капитала соответственно (эти значения определяются имеющимися технологиями);

Производственная функция Кобба-Дугласа была разработана на основе статистических данных. Они свидетельствовали о том, что доля вклада труда и капитала была постоянной на протяжении времени в развитых странах. На сегодняшний день у многих ученых это положение вызывает большие сомнения.

Видео:4.2 Производственная деятельность фирмыСкачать

Эластичность факторов производства

Параметры a и b играют важную роль в расчете предполагаемого объема выпуска товаров по формуле Кобба-Дугласа. Эластичность факторов отражает то, как изменение их соотношения повлияет на физическое производство при прочих равных условиях. Например, если a=0,45, то увеличение на 1% использования трудовых ресурсов приведет к приблизительному росту объема выпуска товаров на 0,45%.

Рассмотрим три основных случая значений, которые могут принимать коэффициенты в формуле:

• a+b=1. В этом случае считается, что производственная функция имеет постоянную отдачу от масштаба. Это означает, что увеличение использования капитала и труда на 100 %, приведет к удвоению общего объема выпуска товаров;
• a+b;
• a+b>1. Этот случай связан с уменьшением отдачи от масштаба.

В условиях совершенной конкуренции и равенства эластичности труда и капитала коэффициенты a и b показывают доли каждого из факторов в общем объеме производства.

Видео:6.2.1. Производственная функцияСкачать

История разработки формулы

Пол Дуглас первоначально занимался изучением вклада человеко-часов и объема капитала в выпуск. Он искал функциональную зависимость между данными показателями. Он поговорил со своим коллегой Чарльзом Коббом и вместе они вывели формулу с одним коэффициентом: Y=A*L b *K 1- b . Ранее данное равенство уже использовалось Кнутом Викселлем. Оценивая результат вычисления с помощью метода наименьших квадратов, Дуглас определил, что экспонента труда равна 0,75. Позже его подтвердил расчет Национального бюро экономических исследований. Дальнейшие работы в области разработки формулы указали на то, что экспоненты труда и капитала не должны быть постоянными. Как следствие, это позволило более точно определять продуктивность.

Самым большой проблемой данной модели оставалось то, что производственная функция выпуска основывалась на слишком маленьком объеме статистических данным, поэтому ей нельзя было полностью доверять. Дуглас решил использовать данные американской переписи населения, который охватывал многие сферы и обеспечивал значительное количество наблюдения. Результаты своих новых исследований для США и других стран ученый представил в 1947 году на заседании Американской экономической ассоциации, президентом которой он являлся. Вскоре Дуглас стал политиком, но плохое здоровье не позволило ему развить свою концепцию дальше. Однако двадцать лет спустя его производственная функция была популяризирована выдающимися экономистами – Полом Самуэльсоном и Робертом Солоу.

Видео:показать, что функция удовлетворяет соотношениюСкачать

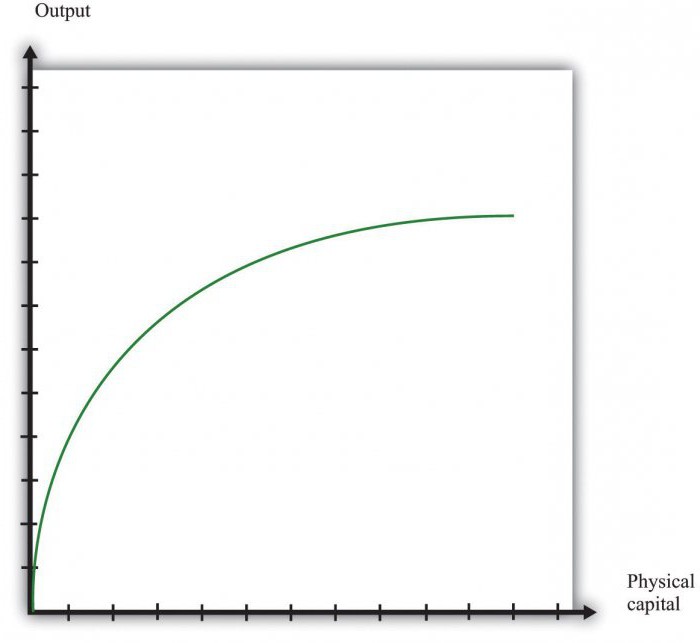
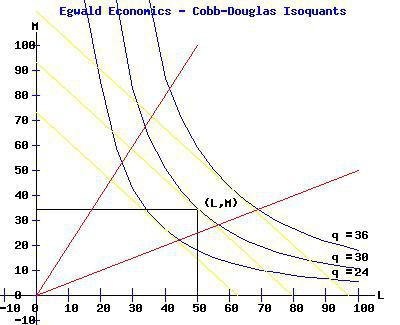
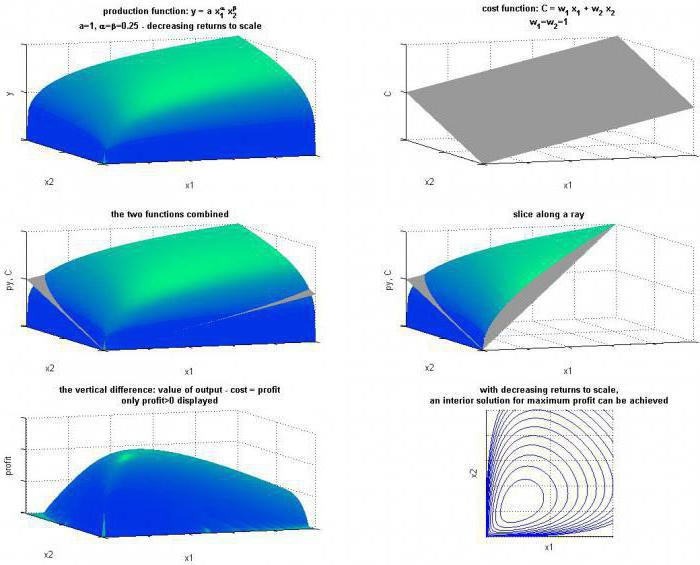
Графическое изображение

Влияние изменений в затратах труда и капитала на объем производства можно отобразить не только с помощью формул, но и изоквант. Последние представляют собой кривые, которые показывают разные комбинации используемых ресурсов, обеспечивающих одинаковый выпуск продукции. Карта изоквант представляет собой альтернативный способ описания производственной функции. Чем дальше от начала координат размещена кривая, тем больший объем выпуска обеспечивают комбинации факторов на ней. Угловой коэффициент любой изокванты может быть выражен пропорцией, где один ресурс может быть замещен другим в процессе производства. Его абсолютное значение равно норме технологического замещения.

Видео:Производственная функция и этапы ее анализаСкачать

Проблемы и критика

Национальное хозяйство – это сложная система, которая включает множество элементов и их взаимосвязей. Поэтому так трудно, если вообще возможно, построить идеальную модель. Основные проблемы использования функции Кобба-Дугласа можно разделить на две сферы:

1. Анализ размерностей. Представители австрийской школы экономики критиковали модель Кобба-Дугласа из-за отсутствия точных показателей. Они утверждали, что в формуле отсутствуют значимые и экономически правильные меры измерения. Однако другие экономисты в ответ Барнетту заявили, что имеющиеся показатели не являются менее точными, чем широко используемые в физике логарифмы температур или квадраты расстояний.
2. Отсутствие микроэкономических оснований. Факторы производственной функции Кобба-Дугласа не были разработаны на основе знания инжиниринга, технологии или управления процессом выпуска. Напротив, ее стали использовать потому, что у нее были красивые математические характеристики, в частности, закон убывающей полезности каждого из факторов и свойство, что расход на производство – это постоянная доля от общей стоимости. И для этого нет микроэкономических оснований. На сегодняшний день многие экономисты стараются строить свои модели на основе поведения отдельных индивидов, а не пытаться наложить свои концепции на целую экономику. Однако современные экономисты (в частности, неокейнсианцы) разработали производственные функции труда и капитала, начиная с микроуровня, которые только подтверждают выводы Кобба и Дугласа. Тем не менее нельзя утверждать, что применимость модели в отдельных отраслях автоматически означает необходимость ее использования для агрегированной экономики.

Видео:7.2.3. Связь эффекта масштаба с производственными функциямиСкачать

Области применения

Несмотря на критику в ее адрес, функция Кобба-Дугласа получила широкое распространение в экономической теории. Ее можно применить для нахождения полезности (u). Если x1 и x2 – это объемы потребления первого и второго товара, то u=x1 a *x2 b .

Видео:Производственная функция. Изокванты и изоклиналиСкачать

Производство как процесс внутри предприятия

Процесс выпуска продукции можно разделить на несколько стадий. Каждая из них имеет свою логику, цели и ключевые фигуры. Важно изучать их отдельно, но понимать, что все стадии являются частью целого. Выделяют следующие процессы внутри предприятия:

• Реальный.
• Распределения доходов.
• Производственный.
• Монетарный.
• Рыночной стоимости.

Видео:Производственная функция | Эффективное комбинирование факторов производстваСкачать

Увеличение выпуска и выработка

Целью любого предприятия является рост собственной прибыльности. А для этого нужно либо увеличить количество единиц производимой продукции, либо сократить расход ресурсов. Увеличение выпуска обычно обозначают в процентах к аналогичному периоду в прошлом. Производственная функция как раз и отображает реальный процесс изготовления товаров на предприятии. Одновременно она показывает механизм создания доходов во время выпуска. Она состоит из двух элементов: изменение объема товаров и продуктивности.

В целом существуют только два основных процесса в экономике – производство и потребление. И столько же основных рыночных субъектов – продавец и покупатель. Благосостояние государства и его жителей зависит от эффективности производства и коммуникации между акторами. Формула Кобба-Дугласа – это первая функция агрегированного производства. С помощью нее стало возможным моделировать не только мелкомасштабные процессы, но и целые отрасли. Ее появление ознаменовало новый этап развития макроэкономики, поскольку она позволила оценить эффективность производства в масштабах всего национального хозяйства государства.

Видео:Производственная функция Задачи с решениями и без.Скачать

Производственная функция Кобба-Дугласа: понятие и формула расчета

Производственная функция Кобба-Дугласа — это модель, которая говорит нам о взаимосвязи между общим продуктом, общей факторной производительностью, количеством труда и капитала и их эластичностью по выпуску.

Производственная функция Кобба-Дугласа является наиболее широко используемой производственной функцией, поскольку позволяет по-разному оценить различные сочетания труда и капитала.

Другие варианты производственных функций, такие как линейная производственная функция и производственная функция с фиксированной пропорцией (Леонтьева), представляют собой экстремальные сценарии.

В первом случае имеет место совершенное замещение между трудом и капиталом, во втором – нулевое замещение.

Производственная функция Кобба-Дугласа была разработана экономистом Полом Дугласом и математиком Чарльзом Коббом.

Видео:Уравнение окружности (1)Скачать

Формула

Математическое уравнение для функции Кобба-Дугласа выглядит следующим образом:

Q = A × K α × L β , где

Q — общий продукт,

K — единицы капитала,

L — единицы труда,

A — общая факторная производительность, а

α и β – показатели эластичности выпуска капитала и труда соответственно.

Исторические данные об общем объеме производства, трудозатратах и реальной стоимости капитала используются для определения A, α и β методом наименьших квадратов.

Общая факторная производительность (A) — это коэффициент, отражающий влияние факторов, отличных от труда и капитала, на общий продукт.

Эластичность выпуска труда (a) и капитала (b) измеряет отклик выпуска на изменения в труде и капитале соответственно, то есть a и b говорят нам о процентном изменении общего объема производства, которое соответствует увеличению труда и капитала соответственно на 1 %.

Функция Кобба-Дугласа представляет собой типичную выпуклую изокванту.

Видео:Парная регрессия: линейная зависимостьСкачать

Предельный продукт труда/капитала

Когда производственная функция Кобба-Дугласа частично дифференцируется относительно L и K, мы получаем значения предельного продукта труда (MP_L) и предельного продукта капитала (MP_K) соответственно:

MP_L = β × A × K α × L β -1

MP_K = α × A × K α-1 × L β

Производственная функция Кобба-Дугласа дает представление об отдаче от масштаба. Историческая основа функции Кобба-Дугласа является ее самой значительной слабостью.

Кроме статистической элегантности, она не имеет под собой никакой практической основы, и предположение о том, что эластичность выпуска труда и капитала и общая факторная производительность в будущем будут такими же, как и в прошлом, увы, не более чем легковесная гипотеза.

🎦 Видео

Составляем уравнение прямой по точкамСкачать

Составляем уравнение оригинала и вычисляем изображениеСкачать