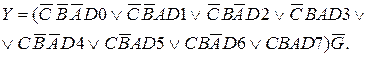Каким логическим уравнением описывается работа мультиплексора 2х1 с управляющим входом (7 видео)

Содержание

Исследование мультиплексоров
Проектирование комбинационных цифровых устройств
Мультиплексор
Уравнение мультиплексора
Исследование мультиплексоров
🎬 Видео

Видео:Шифраторы, дешифраторы. Назначение, принцип работы, типовые схемы.Скачать

Исследование мультиплексоров

1. Ознакомление с принципом работы мультиплексора.

2. Реализация и исследование функциональных модулей на основе мультиплексоров.

Краткие сведения из теории

1. Мультиплексоры. Мультиплексор — комбинационная логическая схема, представляющая собой управляемый переключатель, который подключает к выходу один из информационных входов данных. Номер подключаемого входа равен числу (адресу), определяемому комбинацией логических уровней на входах управления. Кроме информационных и управляющих входов, схемы мультиплексоров содержат вход разрешения, при подаче на который активного уровня мультиплексор переходит в активное состояние. При подаче на вход разрешения пассивного уровня мультиплексор перейдет в пассивное состояние, для которого сигнал на выходе сохраняет постоянное значение независимо от значений информационных и управляющих сигналов. Число информационных входов у мультиплексоров обычно 2, 4, 8 или 16. На рис. 13.9 представлен мультиплексор 8х1 с инверсным входом разрешения G, прямым Y и инверсным W-выходами

2. Уравнение мультиплексора. Функционирование мультиплексора, представленного нарис. 13.9, описывается характеристическим уравнением, связывающим сигнал на выходе (Y) с разрешающим (G), входными информационными (DO. D7) и управляющими (А, В, С) сигналами:

Как видно из уравнения, на мультиплексоре можно реализовать логические функции, для чего нужно определить, какие сигналы и логические константы следует подавать на входы мультиплексора.

3. Реализация заданной функции с помощью мультиплексора. Логическая функция п переменных определена для 2″ комбинация значений переменных. Это позволяет реализовать функцию п-переменных на мультиплексоре, имеющем п-управляющих и 2n информационных входов. В этом случае каждой комбинации значений аргументов соответствует единственный информационный вход мультиплексора, на который подается значение функции. Например, требуется реализовать функцию

Эта функция определена только для 8 комбинаций значений переменных, поэтому для её реализации молено использовать мультиплексор 8х1 с тремя управляющими входами. Составим таблицу истинности функции:

Из таблицы видно, что для реализации функции на мультиплексоре необходимо подать на информационный вход мультиплексора с номером N сигнал, значение которого равно соответствующему значению функции F1, т. е. на входы с номерами 1, 2, 4, 5 следует подать уровень логического нуля, а на остальные — уровень логической единицы. Таким образом, при подаче комбинации логических уровней на управляющие входы мультиплексора, к его выходу подключится вход, значение сигнала на котором равно соответствующему значению функции. Схемная реализация приведена на рис. 13.10. При реализации логических функций на информационные входы можно подавать не только константы, но и изменяющиеся входные сигналы. Так, например, рассмотрим другой способ реализации функции F1, рассмотренной выше. Для этого минимизируем выражение функции:

Составим таблицу истинности функции в зависимости от значений переменных а и b:

Заданную такой таблицей функцию реализуют, как и в предыдущем случае, подав на вход с номером N сигнал, значение которого соответствует значению функции F1. В данном случае сигналы с и с’, соответствующие переменной с, подаются на информаци-

онные входы, как указано в таблице истинности. При этом сокращается число управляющих входов. Схемная реализация такого способа задания функции представлена на рис. 13.11. Так как используются только два адресных входа, управляющий вход С можно заземлить. При этом состояние информационных входов D4. D7 безразлично. Уровень сигнала на выходе схемы определяется комбинацией уровней сигналов в точках А, В, С, соответствующих переменным а, Ь, с. Схема рис.13.11. по существу представляет собой мультиплексор 4х1 с двумя управляющими и четырьмя информационными входами. Если функцию можно представить в виде произведения одночлена на многочлен, то её также можно реализовать при помощи мультиплексора. Как следует из уравнения мультиплексора, сигнал, соответствующий одночлену, нужно подать на вход разрешения. Например, требуется реализовать функцию F2, описываемую следующим выражением:

При реализации данной функции на мультиплексоре сигнал, соответствующий переменной х, следует подать на его разрешающий вход. Рассмотрим, какие сигналы необходимо подать на управляющие входы мультиплексора. Выражение в скобках можно рассматривать как некоторую функцию / пяти переменных: а, Ь, с, d, e, из которых наиболее часто используются переменные а, Ь и с. Поэтому сигналы, соответствующие этим переменным, нужно подать на управляющие входы мультиплексора. Определим, какие сигналы следует подать на информационные входы, чтобы реализовать функцию /. Для этого составим таблицу истинности функции в зависимости от значений переменных а, Ь и с: Из таблицы видно, что на информационные входы с номерами N = 0, 2, 4, 6 нужно подать уровень логического нуля. Сигнал, соответствующий переменной d, нужно подать на входы с номерами N = 1, 5, сигнал, соответствующий переменной e, — на вход с номером 3. Соответствующая схемная реализация представлена на рис. 13.12.

Порядок проведения экспериментов

Эксперимент 1. Исследование мультиплексора.

а). Откройте файл с13_06 со схемой, изображенной на. рис. 13.13. Включите схему. С помощью ключа G установите на входе G мультиплексора уровень логического нуля. Поочередно подавая все возможные комбинации логических уровней при помощи ключей А, В, С на соответствующие входы мультиплексора, для каждой комбинации с помощью логических пробников определите, переключение какого из ключей в левой части схемы изменяет состояние выходов мультиплексора. Обозначение соответствующего входа мультиплексора запишите в таблицу 13.10 в разделе «Результаты экспериментов», указав при этом, как передается входной сигнал на выходы мультиплексора (напрямую или с инверсией). Например, если переключение ключа 4 изменяет состояние выходов мультиплексора, в таблице в строке с соответствующей комбинацией уровней сигналов на входах А, В, С следует записать для выхода Y — D4, для выхода W — D4. б). Установите при помощи ключа G уровень логической единицы на входе G микросхемы. В раздел «Результаты экспериментов» запишите обозначения выводов, которые при переключении соответствующих ключей в левой части схемы не влияют на состояние выходов микросхемы.

Эксперимент 2. Исследование мультиплексора с помощью генератора слов.

Откройте файл с13_07 со схемой, изображенной на рис. 13.14. Включите схему. Подавая в пошаговом режиме слова от генератора слов на входы мультиплексора и наблюдая уровни сигналов на выходах Y и W при помощи логических пробников, заполните таблицу 13.11 в разделе «Результаты экспериментов».

Эксперимент 3. Реализация заданной функции с помощью мультиплексора. а). Определите значение функции F1 для каждой комбинации значений аргументов и заполните графу F1paсч в разделе «Результаты экспериментов». Откройте файл с13_08 со схемой, изображенной на рис. 13.15. Включите схему. Подайте при помощи ключей А, В, С все возможные комбинации логических сигналов на входы мультиплексора и, определяя уровень сигнала на выходе Y логическим пробником F1, заполните графу F1a) в таблице 13.12 в разделе «Результаты экспериментов». Убедитесь, что функция, реализуемая мультиплексором, описывается выражением:

б). Откройте файл с13_09 со схемой, изображенной на. рис. 13.16. Включите схему. Подавая в пошаговом режиме слова от генератора слов на входы мультиплексора и наблюдая уровень сигнала на выходе Y логическим пробником F1, заполните графу F16) в таблице 13.12 в разделе «Результаты экспериментов». Убедитесь, что сигнал на выходе также определяется функцией F1. в). Откройте файл с13_10 со схемой, изображенной на рис. 13.17. Последовательно подавая на входы схемы все возможные комбинации уровней логических сигналов, убедитесь, что уровень логической единицы на выходе появляется только в случаях, когда на входах схемы действуют комбинации, описываемые шестнад-цатеричными эквивалентами 07Н, 09Н, ОСН, ODH, OFH, 13h, 17H, 19Н, 1ВН, 1СН, 1DH, 1FH, при которых функция F2 принимает значение 1.

Эксперимент 4. Исследование мультиплексора 74153.

а). Откройте файл с13_11 со схемой, изображенной на рис. 13.18. Исследуйте работу сдвоенного четырехканального мультиплексора (микросхема 74153). Составьте таблицу функционирования схемы для выходов Y1 и Y2. Для этого установите ключами 1 и 2 уровень логического нуля на входах G1 и G2. Затем в пошаговом режиме последовательно подайте от генератора все слова последовательности для каждой комбинации логических уровней на входах А и В. Для каждого шага определите входы, сигналы с которых проходят на выходы микросхемы. Обозначения входов занесите в таблицу 13.12 в разделе «Результаты экспериментов».

б). При помощи ключа 1 установите уровень логической единицы на входе 1G микросхемы. Подавая на входы микросхемы слова от генератора, определите, какой из выходов микросхемы перестал реагировать на изменение состояния входов. Запишите обозначение этого вывода в раздел «Результаты экспериментов». в). Повторите действия пункта б), установив на входе 2G уровень логической единицы, а на входе 1G — уровень логического нуля.

Эксперимент 1. Исследование мультиплексора. а).

Видео:Мультиплексоры и демультиплексорыСкачать

Проектирование комбинационных цифровых устройств

Видео:Лекция 91. МультиплексорСкачать

Мультиплексор

Мультиплексор — это устройство передающие (подключающие) сигнал одного из входов на выход под управлением входа управления (входов управления).

Условное графическое обозначение (УГО) мультиплексора «2 в 1» представлено в форме «черного ящика» (рис.29):

«А» — вход управления (адресный вход)

«x₀» ч «x₁» — информационные входы

«y» — информационный выход

Рис. 29. УГО мультиплексора на два входа

В зависимости от количества входов мультиплексоры называются «2 в 1», «4 в 1», «8 в 1» и т.д.

Логика работы простейшего мультиплексора «2 в 1» следующая:

1. Если на вход А подать «0», то мультиплексор логически соединяет вход x0 с выходом y, и на выходе y появится сигнал x0 (независимо от того что находится в этот момент на входе x1). Логическая коммутация показана пунктирной линией (рис. 30):

Рис.30. Логика работы MUX при подачи на входе управления «0»

2. Если на вход А подать «1», то мультиплексор логически соединяет вход x1 с выходом y, и на выходе y появится сигнал поданный на вход x1 (в независимости от того что находится в этот момент на входе x0). Логическая коммутация показана пунктирной линией (рис. 31):

Рис. 31. Логика работы MUX при подачи на вход управления «1»

Соответствие может быть реализовано включением светодиода по выходу y и установлением на входе А уровня сигнала «1», на входе x₁ уровня сигнала «1» (рис. 32).

Рис. 32. Логика работы мультиплексора

Выполним проектирование цифрового устройства мультиплексор «2 в 1» используя:

— различные логические элементы;
— только элементы 2И-НЕ;
— только элементы 2ИЛИ-НЕ.

Этап 1. Зададим математическую модель в форме таблицы истинности.

Построим таблицу истинности исходя из логики работы мультиплексора «2 в 1» описанной выше (табл. 14) .

Таблица 14 — Таблица истинности мультиплексора «2 в 1»

Первые три столбца представляют собой возможные комбинации уровня входных сигналов. Заметим, что первые две строчки определяют комбинацию сигналов при наличии на входе управления уровня сигнала «0», (при этом информационный вход x₁ не задействован).

Последние две стройки, наоборот, определяют состояние устройства при наличии на входе управления уровня сигнала «1».

Последний столбец показывает значение логического уровня на выходе с учетом заданных входных сигналов. Так, например, третья строчка (1 — 0 0) означает следующие: на вход управления подан сигнал «1», на вход x₁ подан логический «0», вход x₀ не играет роли, значит, на выходе y появится сигнал входа x₁, т.е. «0».

Этап 2. Построение булевых уравнений.

На основе таблицы истинности 13 построим математическую модель в алгебраической форме булевых уравнений.

Выделим те строки, при которых y принимает значение «1»: строки 3 и 5. Пусть строке 3 соответствует уравнение (минтерм) y₁, а строке 5 уравнение y₂.

Булево уравнение будет иметь вид:

где оператор «v» — дизъюнкция, логическое «ИЛИ».

Строка 3: Вход A имеет значение «0», значит, проставляем инверсию над А, x₀ имеют значения «1», вход x₁ не задействован (не указываем в уравнении для этой строки). Таким образом, для строки 3 уравнение примет следующий вид .

Строка 5: Вход A имеет значение «1», инверсию над А не ставим, вход x₀ не задействован, x₁ имеют значения «1» инверсия не ставится. Итак, для строки 5 уравнение примет следующий вид .

Составим для строки № 3 и № 5 (где y имеет уровень сигнала «1») таблицу значений «минтермов» (табл.15).

Таблица 15 — Таблица значений «минтермов»

«Минтерм» (термин булевой алгебры) — операция логического умножения входных сигналов для строки, где у =1 при условии, что уровень логической «1» принят за «истину».

Тогда булево уравнение запишем в виде:

Полученное уравнение представлено в дизъюнктивной нормальной форме (ДНФ) и является минимальным.

Этап 3. Синтез схемы мультиплексора «2 в 1».

Исходя из полученного булевого уравнения, построение схемы потребует применения следующих элементов:

— инвертора, для получения инверсии сигнала управления A;

— два элемента И, для получения конъюнкций между соответствующими сигналами минтермов ;
— один элемент ИЛИ, для объединения минтермов в единое булево уравнение.

Составим описанную выше схему (рис. 33).

Рис. 33. Синтез схемы мультиплексора «2 в 1»

Рассмотрим синтез схемы выполненный на элементах 2И-НЕ. Для этого приведем уравнение к базису «2И-НЕ».

Поставим над всем уравнением двойную инверсию:

Преобразуем данное уравнение, на основе законов булевой алгебры:

По итоговому уравнению синтезируем схему мультиплексора (рис. 34).

Рис. 34. Схема мультиплексора «2 в 1» на элементах 2И-НЕ

Выполним синтез схемы на элементах 2ИЛИ-НЕ. Для этого приведем уравнение к базису «2ИЛИ-НЕ».

Поставим над всем уравнением и над каждым выражением конъюнкций в дизъюнкции двойную инверсию:

Преобразуем данное уравнение, на основе законов булевой алгебры:

По итоговому уравнению синтезируем схему мультиплексора (рис. 35).

Рис. 35. Схема мультиплексора «2 в 1» на элементах 2ИЛИ-НЕ

УГО мультиплексора «1 в 4» показан на рис. 36.

Рис. 36. Схема мультиплексора «2 в 1» на элементах 2ИЛИ-НЕ

Отметим, что здесь присутствуют уже два входа управления, что даёт возможность управления 2 2 = 4 входами. Поясним это, составив таблицу истинности (табл. 16).

Таблица 16 — Таблица истинности мультиплексора «1 в 4»

Видео:Буфер, регистр, мультиплексор, дешифратор, счётчик, сдвиговый регистр, линия задержки.Скачать

Уравнение мультиплексора

Дата добавления: 2014-11-27 ; просмотров: 2874 ; Нарушение авторских прав

Простейший мультиплексор 2–1 применяется довольно часто. Как было показано, его работа описывается уравнением

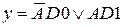
где D0, D1 информационные входы, A – вход управления.

Функционирование мультиплексора, представленного на рис. 3.3,а, описывается уравнением

связывающим сигнал на выходе Y с входными информационными D0,…,D3 и управляющими А, В сигналами.

Для мультиплексора рис. 3.3,б уравнение будет таким

Как видно из этого уравнения, при E = 0 значение выходного сигнала Y будет равно 0, независимо от значений входных и управляющих сигналов.

В интегральном исполнении число информационных входов у мультиплексоров обычно 2, 4, 8 или 16.

На рис. 3.4 представлен мультиплексор 8-1 с инверсным входом разрешения G’, прямым Y и инверсным W выходами ( ).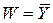

Функционирование мультиплексора, представленного на рис. 3.4, описывается уравнением

Рис. 3.3. Схемы мультиплексоров 4-1:

а) без входа разрешения; б) с входом разрешения Е

Видео:Лекция 94. Применение мультиплексораСкачать

Исследование мультиплексоров

Мультиплексоры. Мультиплексор — комбинационная логическая схема, представляющая собой управляемый переключатель, который подключает к выходу один из информационных входов данных. Номер подключаемого входа равен числу (адресу), определяемому комбинацией логических уровней на входах управления. Кроме информационных и управляющих входов, схемы мультиплексоров содержат вход разрешения, при подаче на который активного уровня мультиплексор переходит в активное состояние. При подаче на вход разрешения пассивного уровня мультиплексор перейдет в пассивное состояние, для которого сигнал на выходе сохраняет постоянное значение независимо от значений информационных и управляющих сигналов. Число информационных входов у мультиплексоров обычно 2, 4, 8 или 1 На рис. 13.9 представлен мультиплексор 8х1 с инверсным входом разрешения G, прямым Y и инверсным W-выходами

Уравнение мультиплексора. Функционирование мультиплексора, представленного нарис. 13.9, описывается характеристическим уравнением, связывающим сигнал на выходе (Y) с разрешающим (G), входными информационными (DO. D7) и управляющими (А, В, С) сигналами:

Реализация заданной функции с помощью мультиплексора. Логическая функция п переменных определена для 2″ комбинация значений переменных. Это позволяет реализовать функцию п-переменных на мультиплексоре, имеющем п-управляющих и 2n информационных входов. В этом случае каждой комбинации значений аргументов соответствует единственный информационный вход мультиплексора, на который подается значение функции. Например, требуется реализовать функцию

Из таблицы видно, что для реализации функции на мультиплексоре необходимо подать на информационный вход мультиплексора с номером N сигнал, значение которого равно соответствующему значению функции F1, на входы с номерами 1, 2, 4, 5 следует подать уровень логического нуля, а на остальные — уровень логической единицы. Таким образом, при подаче комбинации логических уровней на управляющие входы мультиплексора, к его выходу подключится вход, значение сигнала на котором равно соответствующему значению функции. Схемная реализация приведена на рис. При реализации логических функций на информационные входы можно подавать не только константы, но и изменяющиеся входные сигналы. Так, например, рассмотрим другой способ реализации функции F1, рассмотренной выше. Для этого минимизируем выражение функции:

Заданную такой таблицей функцию реализуют, как и в предыдущем случае, подав на вход с номером N сигнал, значение которого соответствует значению функции F В данном случае сигналы с и с’, соответствующие переменной с, подаются на информаци-

онные входы, как указано в таблице истинности. При этом сокращается число управляющих входов. Схемная реализация такого способа задания функции представлена на рис. Так как используются только два адресных входа, управляющий вход С можно заземлить. При этом состояние информационных входов D4. D7 безразлично. Уровень сигнала на выходе схемы определяется комбинацией уровней сигналов в точках А, В, С, соответствующих переменным а, Ь, с. Схема рис. по существу представляет собой мультиплексор 4х1 с двумя управляющими и четырьмя информационными входами. Если функцию можно представить в виде произведения одночлена на многочлен, то её также можно реализовать при помощи мультиплексора. Как следует из уравнения мультиплексора, сигнал, соответствующий одночлену, нужно подать на вход разрешения. Например, требуется реализовать функцию F2, описываемую следующим выражением:

При реализации данной функции на мультиплексоре сигнал, соответствующий переменной х, следует подать на его разрешающий вход. Рассмотрим, какие сигналы необходимо подать на управляющие входы мультиплексора. Выражение в скобках можно рассматривать как некоторую функцию / пяти переменных: а, Ь, с, d, e, из которых наиболее часто используются переменные а, Ь и с. Поэтому сигналы, соответствующие этим переменным, нужно подать на управляющие входы мультиплексора. Определим, какие сигналы следует подать на информационные входы, чтобы реализовать функцию /. Для этого составим таблицу истинности функции в зависимости от значений переменных а, Ь и с: Из таблицы видно, что на информационные входы с номерами N = 0, 2, 4, 6 нужно подать уровень логического нуля. Сигнал, соответствующий переменной d, нужно подать на входы с номерами N = 1, 5, сигнал, соответствующий переменной e, — на вход с номером Соответствующая схемная реализация представлена на рис.

а). Откройте файл с13_06 со схемой, изображенной на. рис. Включите схему. С помощью ключа G установите на входе G мультиплексора уровень логического нуля. Поочередно подавая все возможные комбинации логических уровней при помощи ключей А, В, С на соответствующие входы мультиплексора, для каждой комбинации с помощью логических пробников определите, переключение какого из ключей в левой части схемы изменяет состояние выходов мультиплексора. Обозначение соответствующего входа мультиплексора запишите в таблицу 13.10 в разделе «Результаты экспериментов», указав при этом, как передается входной сигнал на выходы мультиплексора (напрямую или с инверсией). Например, если переключение ключа 4 изменяет состояние выходов мультиплексора, в таблице в строке с соответствующей комбинацией уровней сигналов на входах А, В, С следует записать для выхода Y — D4, для выхода W — D б). Установите при помощи ключа G уровень логической единицы на входе G микросхемы. В раздел «Результаты экспериментов» запишите обозначения выводов, которые при переключении соответствующих ключей в левой части схемы не влияют на состояние выходов микросхемы.