- теория по физике 🧲 гидростатика
- Закон Архимеда
- Воздухоплавание
- Архимедова сила и законы Ньютона
- Условия плавания тел
- Варианты условий задач на условия плавания тел
- Статика. Условие плавания тел.
- Закон Архимеда и условия плавания тел
- Жидкость и гидростатическое давление
- Закон Архимеда
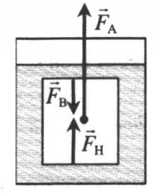
- Силы, действующие на погруженное в жидкость тело
- Когда тела будут плавать?
- Где используется рассмотренное явление?
- Пример решения задачи
- Условия плавания тел
- Сила: что это за величина
- Закон Архимеда
- Плавание тел
- 🎦 Видео
теория по физике 🧲 гидростатика
Архимедова сила (выталкивающая сила, подъемная сила) — сила, с которой жидкость или газ выталкивают погруженное в них тело.
Полезно знать и понимать!
- Причина возникновения выталкивающей силы: нижняя грань тела находится на большей глубине, чем верхняя, поэтому давление жидкости снизу больше, чем сверху. Из-за разницы в давлениях возникает выталкивающая сила.
- Архимедова сила всегда направлена вертикально вверх.
- Архимедова сила равна разности сил давления на нижнюю и верхнюю грани:
- Также выталкивающая сила равна разности веса тела в воздухе и веса тела в жидкости:
- Модуль выталкивающей силы определяется с помощью закона Архимеда.
Закон Архимеда
Выталкивающая сила равна весу вытесненной жидкости.
Частные случаи определения архимедовой силы
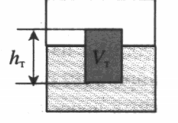
Полное погружение
Архимедова сила равна произведению плотности жидкости, объема тела и ускорения свободного падения:
Vт — объем погруженного в жидкость тела.
Неполное погружение
Архимедова сила равна произведению плотности жидкости, объема погруженной части тела и ускорения свободного падения:
Vп.ч. — объем погруженной в жидкость части тела.
Внимание! Если тело погружено в газ, то в формуле нужно использовать плотность этого газа.
Пример №1. При взвешивании груза в воздухе показание динамометра равно 1 Н. При опускании груза в воду показание динамометра уменьшается до 0,6 Н. Найдите значение выталкивающей силы.
Выталкивающая сила равна разности веса тела в воздухе и веса тело в воде. Следовательно:
Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

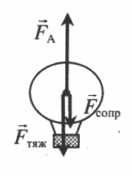
Воздухоплавание
Подъемной силой воздушного шара служит архимедова сила, равная:
Подъемной силе противостоят сила тяжести и сила сопротивления воздуха:
Управление шаром:
- чтобы взлететь, шар заполняют нагретым воздухом или газом, плотность которого меньше плотности окружающего воздуха;
- чтобы увеличить высоту полета, с шара сбрасывают балласт;
- чтобы спуститься на землю, газ охлаждают.
Пример №2. Аэростат объемом 1000 м 3 заполнен гелием. Плотность гелия 0,18 кг/м 3 , плотность воздуха 1,29 кг/м 3 . Какая выталкивающая сила действует на аэростат?
Выталкивающая сила зависит только от плотности
Окружающая среда — это комплекс окружающих человека или другой живой организм физических, географических, биологических, социальных, культурных и политических условий, который определяет форму и характер его существования.
Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Архимедова сила и законы Ньютона
Если тело полностью погружено в жидкость (или газ):
- Архимедова сила равна: FA = ρжVтg.
- Сила тяжести, действующая на тело: Fтяж = mg = ρтVтg.
Частный случай
Определить минимальную массу груза, который следует положить на плоскую однородную льдину площадью S, чтобы она полностью погрузилась в воду. Толщина льдины h, а плотность льда ρл, плотность воды ρв.
Второй закон Ньютона в векторной форме для льдины, полностью погруженной в воду (она не тонет и не всплывает):
→ F A + → F т я ж = 0
Так как эти силы направлены в противоположные стороны:
Архимедова сила, действующая только на льдину, равна:
Сила тяжести равна сумме масс льдины и груза:
Массу льдины можно выразить через произведение ее плотности на объем, равные произведению ее площади на толщину:
Пример №3. Какую силу надо приложить, чтобы поднять под водой камень, масса которого 30 кг, а объем 12 000 см 3 ?
12 000 куб. см = 0,012 куб. м
Чтобы поднять под водой камень, потребуется сила, равная разности силе тяжести и архимедовой силы, действующей на этот камень:
Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Условия плавания тел
На любое тело, погруженное в жидкость или газ, действуют две противоположно направленные силы: сила тяжести и архимедова сила. Направление движения тела зависит от того, какая из этих сил больше по модулю:
- Тело тонет, если: mg > FA; ρт > ρж.
- Тело плавает в толще среды, если: mg = FA; ρт = ρж.
- Тело всплывает, если: mg
Если тело плавает на поверхности:
- Архимедова сила и сила тяжести, действующие на него, равны: FA= Fтяж.
- Сила тяжести равна: Fтяж = mg = ρтVтg.
- Архимедова сила равна: FA = ρжVп.ч.g.
- Взаимосвязь между объемом и высотой тела правильной формы: V = Sh.
Варианты условий задач на условия плавания тел
Сплошное тело объемом Vт плавает в воде. Причем под водой находится 3/4 его объема. Определите силу тяжести, действующую на тело. Плотность воды ρв.
Второй закон Ньютона в векторной форме:
→ F A + → F т я ж = 0
Отсюда (проекция на вертикальную ось):
Какая часть (в процентах) айсберга находится под водой? Плотность льда ρл, а воды ρв.
Второй закон Ньютона в векторной форме:
→ F A + → F т я ж = 0
Отсюда (проекция на вертикальную ось):
Ускорение свободного падения взаимоуничтожается. Чтобы найти погруженную часть айсберга в процентах, нужно:
V п . ч . V л . . = ρ л ρ в . .
Найденное отношение остается умножить на 100%.
Полое тело плотностью ρтплавает в воде, погрузившись на 1/5 своего объема. Найдите объем полости Vп, если объем тела Vт, а плотность воды ρв.
Второй закон Ньютона в векторной форме:
→ F A + → F т я ж = 0
Отсюда (проекция на вертикальную ось):
Преобразовав выражение, получим:
V п = V т ( 5 ρ т − ρ в ) 5 ρ т . .
Пример №4. Кубик массой 40 г и объемом 250 см 3 плавает на поверхности воды. Найдите значение выталкивающей силы, действующей на кубик.
250 см 3 = 250∙10 –6 м 3
Так как тело плавает, Архимедова сила будет равна по модулю силе тяжести, которая определяется формулой:

Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Записать условие плавания тел.
- На основании условия плавания тел сделать вывод о том, как изменятся указанные физические величины.
Решение
По условию задачи деревянный шарик плавает на поверхности воды. Но это возможно, лишь когда архимедова сила равна силе тяжести:
Если шарик будет плавать в подсолнечном масле, также можно применить условие плавания тел:
Сила тяжести зависит только от массы тела, которая остается неизменной. Поэтому сила тяжести тоже не меняется. Но из этого следует:
Это возможно благодаря тому, что объем погруженной части шарика в масло будет больше объема погруженной части шарика в воду. Этим компенсируется разница в плотностях жидкостей, но архимедова сила при этом остается неизменной.
Верный ответ: 33.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Ученик изучает силу Архимеда, действующую на тела, полностью погружённые в жидкость. В его распоряжении имеется установка, состоящая из ёмкости с водой и сплошного деревянного шарика объёмом 30 см 3 . Какая из следующих установок необходима ещё ученику для того, чтобы на опыте обнаружить зависимость силы Архимеда от объёма тела?
| № «>№ установки | Жидкость, налитая в ёмкость | Объём шарика | Материал, из которого сделан шарик |
| 1 | вода | 30 см 3 | сталь |
| 2 | вода | 20 см 3 | дерево |
| 3 | керосин | 20 см 3 | дерево |
| 4 | подсолнечное масло | 30 см 3 | сталь |
а) установка № «>№ 1
б) установка № «>№ 2
в) установка № «>№ 3
г) установка № «>№ 4
Алгоритм решения
- Сделать анализ задачи. Определить, какие величины в опыте остаются постоянными.
- Определить, какие величины должны быть в опыте переменными.
Решение
Ученик изучает силу Архимеда, действующую на тела, полностью погружённые в жидкость. В формулировке слово «жидкость» используется в единственном числе. Следовательно, жидкость во всех опытах будет одной и той же (плотность жидкости будет постоянной). У ученика уже есть установка, в которую входит емкость с водой. Поэтому во второй установке в качестве жидкости тоже должна использоваться вода. Варианты 3 и 4 исключаются.
В формулировки задачи также говорится о «телах». Они могут быть выполнены из разных материалов, и они могут иметь разный объем. Но известно, что архимедова сила зависит только от объема тела. Поэтому во второй установке нужно использовать тело другого объема. В вариантах 1 и 2 этому условию соответствует деревянный шарик объемом 20 куб. см (так как в первой установке используется шарик объемом 30 куб. см).
Отсюда верный ответ: б.
pазбирался: Алиса Никитина | обсудить разбор | оценить
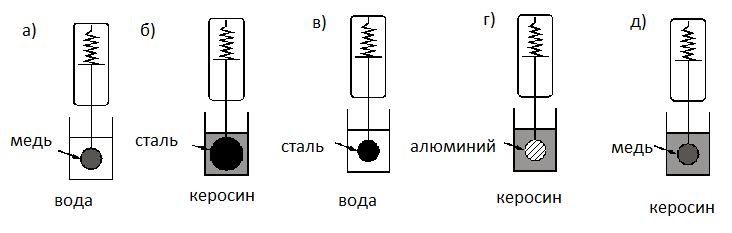
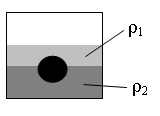
Необходимо экспериментально изучить зависимость силы Архимеда, действующей на тело, погружённое в жидкость, от плотности жидкости.
Какие две установки следует использовать для проведения такого исследования?
Алгоритм решения
- Установить цели опыта.
- Сделать вывод о том, какие величины в опыте должны быть постоянными, а какие — переменными.
- Выбрать установки, соответствующие выводу.
Решение
В опыте нужно изучить зависимость силы Архимеда, действующей на тело, погружённое в жидкость, от плотности жидкости. Это значит, что плотность жидкости — величина переменная. Все остальные величины при этом должны оставаться постоянным. Поэтому нам нужны установки с разными жидкостями, но одинаковыми телами. Этому условию соответствуют две установки: «а» и «д».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Видео:Уравнение состояния идеального газаСкачать

Статика. Условие плавания тел.
Плавание тел — состояние равновесия твердого тела, частично или полностью погруженного в жидкость (или газ).
Основная задача теории плавания тел — определение равновесия тела, погруженного в жидкость, выяснение условий устойчивости равновесия. На простейшие условия плавания тел указывает закон Архимеда. Рассмотрим эти условия.
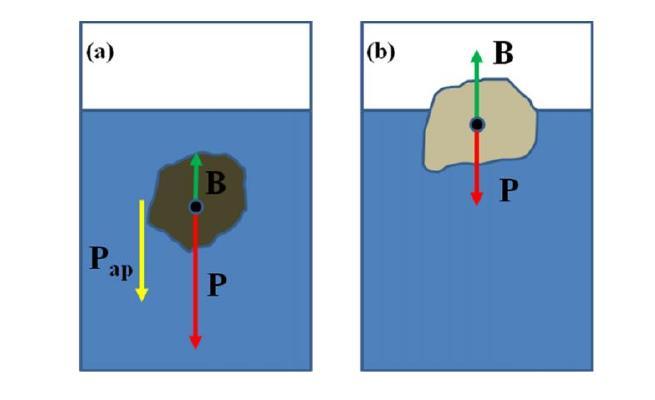
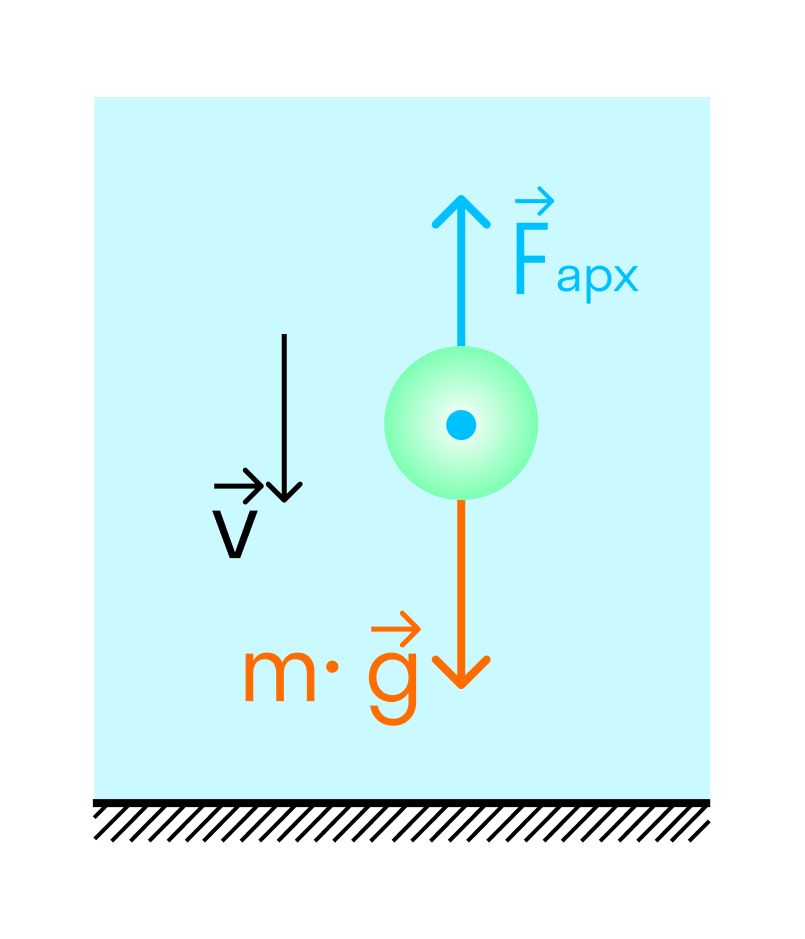
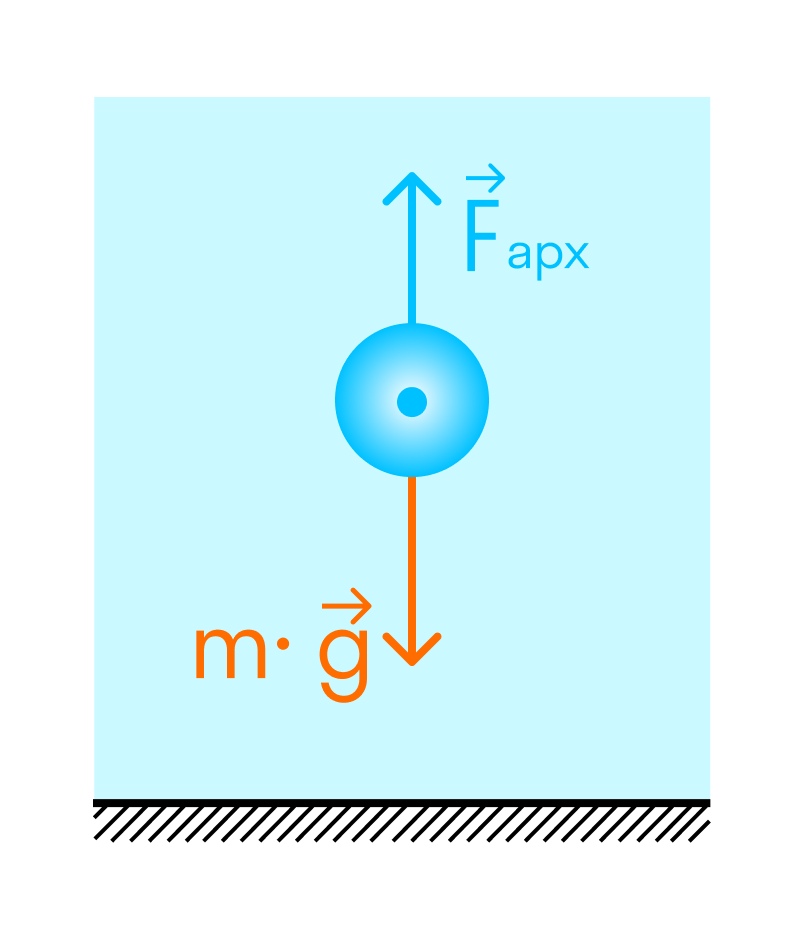
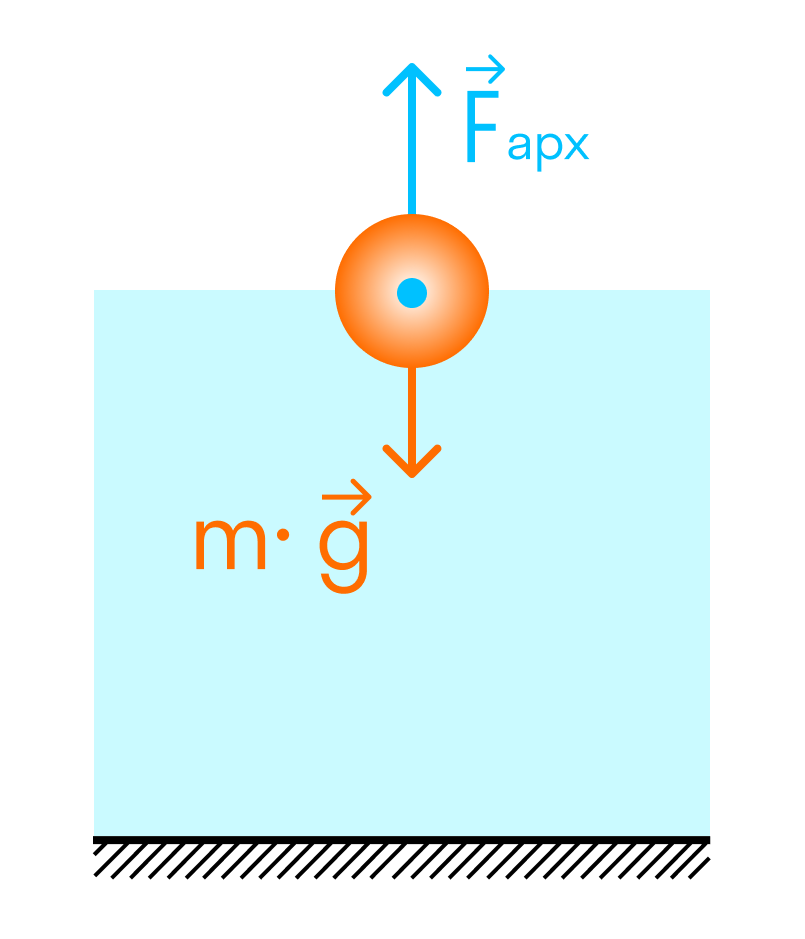
Как известно, на все тела, погруженные в жидкость, действует сила Архимеда FA (выталкивающая сила), направленная вертикально вверх, однако всплывают далеко не все. Чтобы понять, почему одни тела всплывают, а другие тонут, необходимо учесть еще одну силу, действующую на все тела, — силу тяжести F т которая направлена вертикально вниз, т. е. противоположно FA. Если тело оставить внутри жидкости в состоянии покоя, то оно начнет двигаться в сторону, в которую направлена большая из сил. При этом возможны следующие случаи:
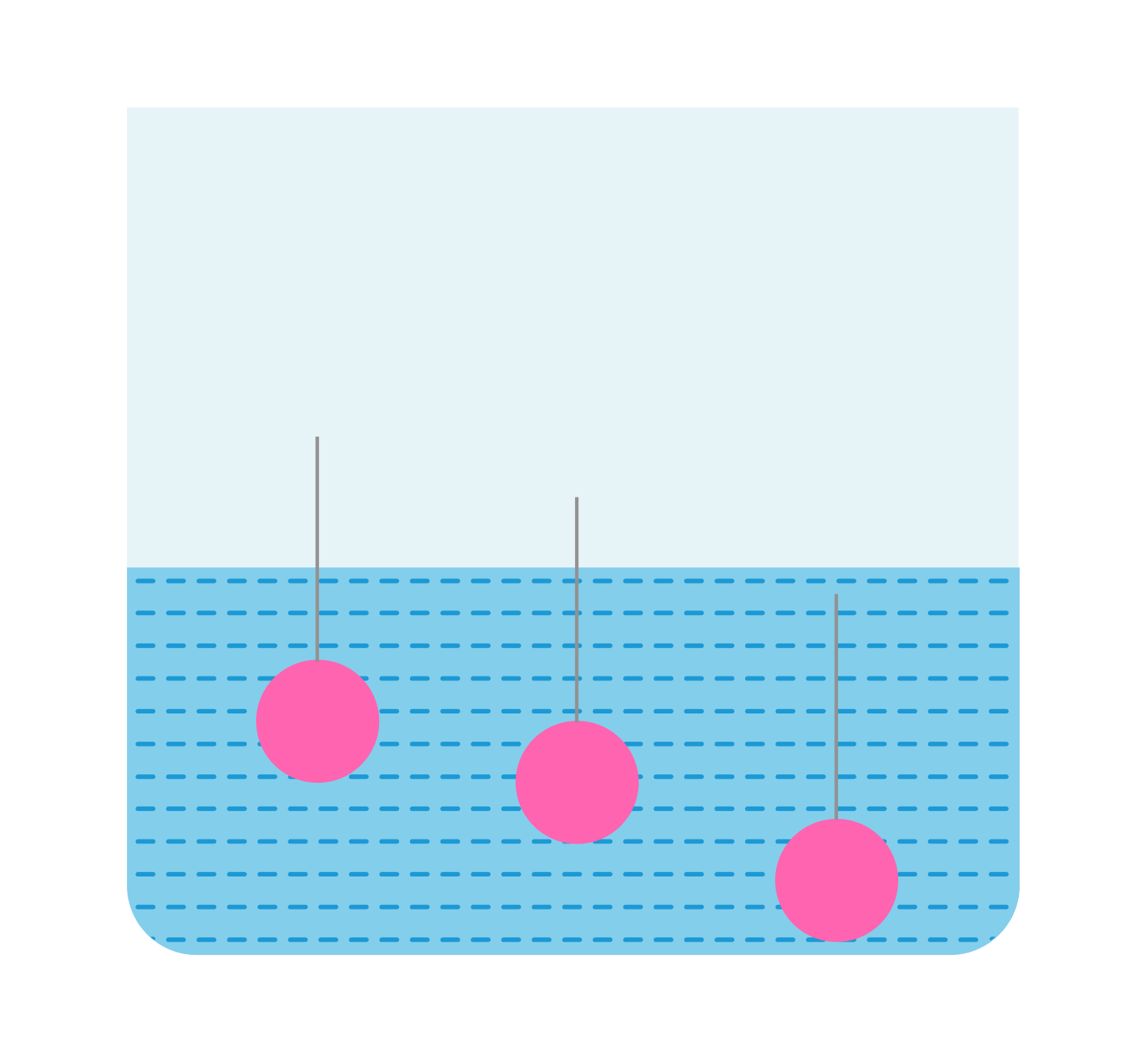
- если архимедова сила меньше силы тяжести (FA Fт), то тело всплывет (рис. б);
3) если архимедова сила равна силе тяжести (FA = Fт), то тело останется в покое. Последнее условие является условием равновесия тела в жидкости:
Равенство FA = Fт выражает условие плавания тел: для того, чтобы тело плавало, необходимо, чтобы действующая на него сила тяжести уравновешивалась архимедовой (выталкивающей) силой.
Условию плавания тел можно придать другую форму. Представим архимедову силу в виде:
где ρж — плотность жидкости, Vm — объем жидкости, вытесненный телом, g — ускорение свободного падения. Силу тяжести, действующую на тело, тоже можно выразить через объем V и плотность тела ρ:
Разделив обе части этого равенства на g, получим условие плавание тел в новой форме:
Из полученного соотношения можно вывести два важных следствия.
1. Для того чтобы тело плавало, будучи полностью погруженным в жидкость, необходимо, чтобы плотность тела была равна плотности жидкости.
2. Для того чтобы тело плавало, частично выступая над поверхностью жидкости, необходимо, чтобы плотность тела была меньше плотности жидкости.
При ρ > ρж плавание тел невозможно, так как в этом случае сила тяжести превышает архимедову силу, и тело тонет.
Что будет происходить с телом, у которого ρ возд V g,
Если эта сила окажется больше силы тяжести, действующей на тело, то тело взлетит. На этом основано воздухоплавание.
Летательные аппараты, применяемые в воздухоплавании, называют аэростатами (от греч. aer — воздух, status — стоящий). Неуправляемые аэростаты свободного полета с оболочкой, имеющей форму шара, называют воздушными шарами. Для исследования верхних слоев атмосферы (стратосферы) еще не так давно применялись огромные воздушные шары — стратостаты. Управляемые аэростаты (имеющие двигатель и воздушные винты) называют дирижаблями.
Воздушный шар не только сам поднимается вверх, но может поднять и некоторый груз: кабину, людей, приборы. Для того, чтобы определить, какой груз способен поднять воздушный тар, следует знать его подъемную силу. Подъемная сила воздушного шара равна разности между архимедовой силой и действующей на шар силой тяжести:
Чем меньше плотность газа, наполняющего воздушный шар данного объема, тем меньше действующая на него сила тяжести и тем больше возникающая подъемная сила. Воздушные шары можно наполнять гелием, водородом или нагретым воздухом. Хотя у водорода меньше плотность, чем у гелия, все же чаще в целях безопасности применяют гелий (водород — горючий газ).
Гораздо проще осуществить подъем и спуск шара, наполненного горячим воздухом. Для этого под отверстием, находящимся в нижней части шара, располагают горелку. Она позволяет регулировать температуру воздуха, а значит, и его плотность и подъемную силу.
Можно подобрать такую температуру шара, при которой вес шара и кабины будет равен выталкивающей силе. Тогда шар повиснет в воздухе, и с него будет легко проводить наблюдения.
Видео:Закон Архимеда ● 1Скачать

Закон Архимеда и условия плавания тел
Каждый знает, что одни тела, брошенные в воду, тонут, другие же предметы остаются на поверхности жидкости и плавают в ней. В чем заключается физическая причина такого поведения? На этот вопрос ответит данная статья, в которой рассматриваются условия плавания тел.
Видео:Физика. 10 класс. Уравнение состояния идеального газа /23.11.2020/Скачать

Жидкость и гидростатическое давление
Прежде чем излагать условия плавания тел, следует изучить свойства среды, в которой они находятся. Жидкость является неупорядоченным состоянием вещества, в котором молекулы и атомы имеют энергию связи, приблизительно равную их кинетической энергии. Последний факт позволяет им свободно перемещаться по всему объему жидкости. При этом для указанного перемещения не существует определенного направления. То есть каждая молекула смещается равновероятно на любой вектор в трехмерном пространстве.

Если рассмотреть микроскопический объем жидкости внутри нее, то на него со всех сторон молекулы будут оказывать давление. Все давления равны по величине и противоположны по направлению, поэтому они уравновешиваются, а рассматриваемый объем находится в покое.

Действие силы тяжести приводит к появлению так называемого гидростатического давления (для газов оно называется аэростатическим). Возникает это давление по причине того, что верхние слои жидкости давят своим весом на нижние. Гидростатическое давление Pg рассчитывается по формуле:
Здесь ρ — плотность жидкости, h — глубина, g=9,81 м/с2. Таким образом, чем больше глубина, тем выше величина Pg.
Видео:Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Закон Архимеда
Условия плавания тел тесным образом связаны с законом, открытым древнегреческим философом Архимедом. Этот закон можно сформулировать так: всякое твердое тело, погруженное частично или полностью в текучую субстанцию (газ или жидкость) испытывает выталкивающую силу, величина которой равна весу вытесненной субстанции. Отметим, что закон справедлив как для жидкостей, так и для газов. Указанная выталкивающая сила получила название архимедовой.
Причину появления силы Архимеда можно понять, если мысленно провести следующий эксперимент: предположим, что у нас имеется некоторое твердое тело, которое мы погружаем полностью в жидкость, например, в воду. Будем считать, что тело ограничено тремя поверхностями: боковой, верхней и нижней. Гидростатическое давление действует на все эти поверхности, однако его результирующая величина на поверхность боковую будет равна нулю.
На низ тела действует гидростатическое давление, направленное вверх. На верх тела оно также действует, но направлено вниз. Разница этих давлений приводит к образованию выталкивающей силы FA. Для рассматриваемого эксперимента можно записать следующее выражение:
FA = (P2 — P1)*S = ρ*g*S*(h2-h1) = ρ*g*V.
Здесь S — площадь верхней и нижней поверхностей, h2 и h1 — глубины, на которых находятся нижняя и верхняя поверхности тела, соответственно. Величина V — это объем тела (здесь для простоты мы предположили, что оно имеет форму прямоугольной призмы).
Таким образом, мы получили формулу для определения архимедовой силы. Заметим, что произведение плотности на объем вытесненной жидкости (в эксперименте он равен объему тела) — это масса жидкости.
Видео:Уравнение состояния идеального газа. Практическая часть. 10 класс.Скачать

Силы, действующие на погруженное в жидкость тело
Как уже отмечалось, архимедова сила и условия плавания тел связаны между собой. Рассмотрим эту связь с точки зрения математики.
Первый закон Ньютона гласит, что тело будет сохранять состояние покоя, если на него не действуют внешние силы. Применительно к случаю погруженного в жидкость тела можно сказать, что оно будет плавать, когда все силы, которые оказывают на него воздействие, уравновесят друг друга. Таких сил всего две:
Если первая будет больше второй, то тело никогда не сможет плавать и будет тонуть. Если же вторая больше первой, то тело никогда не сможет утонуть. Чтобы погрузить его в жидкость полностью, придется приложить некоторое внешнее усилие.
Физика условия плавания тел заключается в численном соотношении рассмотренных сил.
Видео:идеальный газ УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗАСкачать

Когда тела будут плавать?
Выше уже было названо основное условие плавания тел. Здесь рассмотрим его с математической точки зрения и получим некоторые важные выводы.
Тело будет находиться в равновесии в жидкости, если его вес и архимедова сила равны:
Здесь m — масса тела, ρl, Vl — плотность жидкости и ее вытесненный объем. Поскольку тело погружено полностью в субстанцию, то справедливо равенство:
Здесь Vs — объем тела. Записывая массу m через плотность и объем тела, получаем:
Мы получили простую формулу, отражающую условие плавания тел в жидкости. Оказывается, что плавучесть тел не зависит от их массы, формы, объема. И даже не зависит от материала, из которого они сделаны. Плавучесть определяется лишь соотношением между средней плотностью тела и жидкости. Если плотность ρs будет больше, чем ρl, то сила тяжести превысит величину выталкивания. И тело начнет тонуть. Наоборот, если ρs будет меньше ρl, то тело останется на поверхности жидкости.
Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Где используется рассмотренное явление?
Закон Архимеда находит применение в ряде природных явлений и технологических решений. Перечислим лишь некоторые из них:
- Плавание кораблей в воде и аэростатов в воздухе было бы невозможным без присутствия выталкивающей силы. Хотя корабль сделан из материалов, плотность которых намного больше, чем эта величина для воды, но он имеет внутри себя много пустот (каюты, трюм), заполненных воздухом. Последний факт приводит к тому, что средняя плотность корабля оказывается меньше, чем воды.
- Изменение глубины погружения рыб обусловлено изменением их средней плотности за счет сокращения или раздувания плавательного пузыря.
- Измерительный прибор, служащий для определения содержания спирта или проверки чистоты молока, использует для своего функционирования принцип Архимеда.
Видео:СИЛА АРХИМЕДА. ЕГЭ Физика. Николай Ньютон. ТехноскулСкачать

Пример решения задачи
Применим изложенный теоретический материал для решения практической задачи. Известно, что куб со стороной 20 см имеет массу 7,2 кг. Будет ли плавать этот куб в воде?
Чтобы ответить на вопрос задачи, следует воспользоваться условием плавания тел. Для этого необходимо вычислить плотность куба и сравнить ее с этой величиной для пресной воды (плотность 1 г/см3). Имеем:
ρs = m/V = m/a3 = 7200/203 = 0,9 г/см3.
Плотность куба ρs на 10 % меньше, чем эта величина для воды, поэтому куб плавать в жидкости будет.
Видео:Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Условия плавания тел
О чем эта статья:
Видео:Уравнение состояния идеального газаСкачать

Сила: что это за величина
Перед тем, как разобраться в процессе плавания тел, нужно понять, что такое сила.
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причина любого действия или взаимодействия — ее величество сила.
- Сила — это физическая векторная величина, которая воздействует на данное тело со стороны других тел.
Она измеряется в Ньютонах — единице измерения, которую назвали в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В этом случае результат выражается в направлении движения.
Видео:Физика 10 класс: Уравнение состояния идеального газаСкачать

Закон Архимеда
Этот закон известен преимущественно не своей формулировкой, а историей его возникновения.
Легенда гласит, что царь Герон II попросил Архимеда определить, из чистого ли золота сделана его корона, при этом, не причиняя вреда самой короне. То есть, нельзя ее расплавить или в чем-нибудь растворить.
Взвесить корону Архимеду труда не составило, но этого было мало — нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото.
Это можно сделать по формуле плотности.
Формула плотности тела
ρ — плотность тела [кг/м 3 ]
m — масса тела [кг]
V — объем тела [м 3 ]
Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну — и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему.
Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый закричал «Эврика!» и побежал докладывать о своей победе в царский дворец (по легенде он даже не оделся).
Выталкивающая сила, действующая на тело, погруженное в жидкость, равна по модулю весу вытесненной жидкости и противоположно ему направлена.
На поверхность твердого тела, погруженного в жидкость или газ, действуют силы давления. Эти силы увеличиваются с глубиной погружения, и на нижнюю часть тела будет действовать со стороны жидкости большая сила, чем на верхнюю.
Равнодействующая всех сил давления, действующих на поверхность тела со стороны жидкости, называется выталкивающей силой или силой Архимеда. Истинная причина появления выталкивающей силы — наличие различного гидростатического давления в разных точках жидкости.
Сила Архимеда
ρ ж — плотность жидкости [кг/м 3 ]
V погр — объем погруженной части тела [м 3 ]
g — ускорение свободного падения [м/с 2 ]
На планете Земля: g = 9,8 м/с 2
А теперь давайте порешаем задачки.
Задача 1
В сосуд погружены три железных шарика равных объемов. Одинаковы ли силы, выталкивающие шарики? (Плотность жидкости вследствие ничтожно малой сжимаемости на любой глубине считать примерно одинаковой).
Решение:
Да, так как объемы одинаковы, а архимедова сила зависит от объема погруженной части тела, а не от глубины.
Задача 2
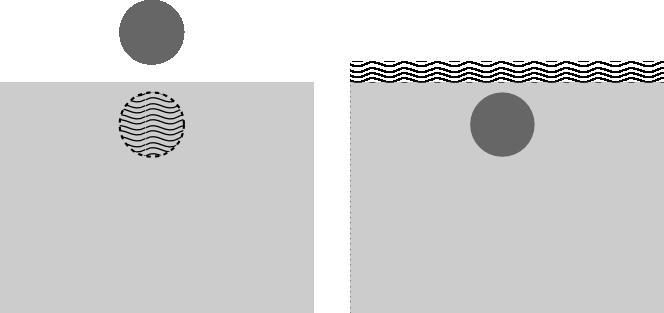
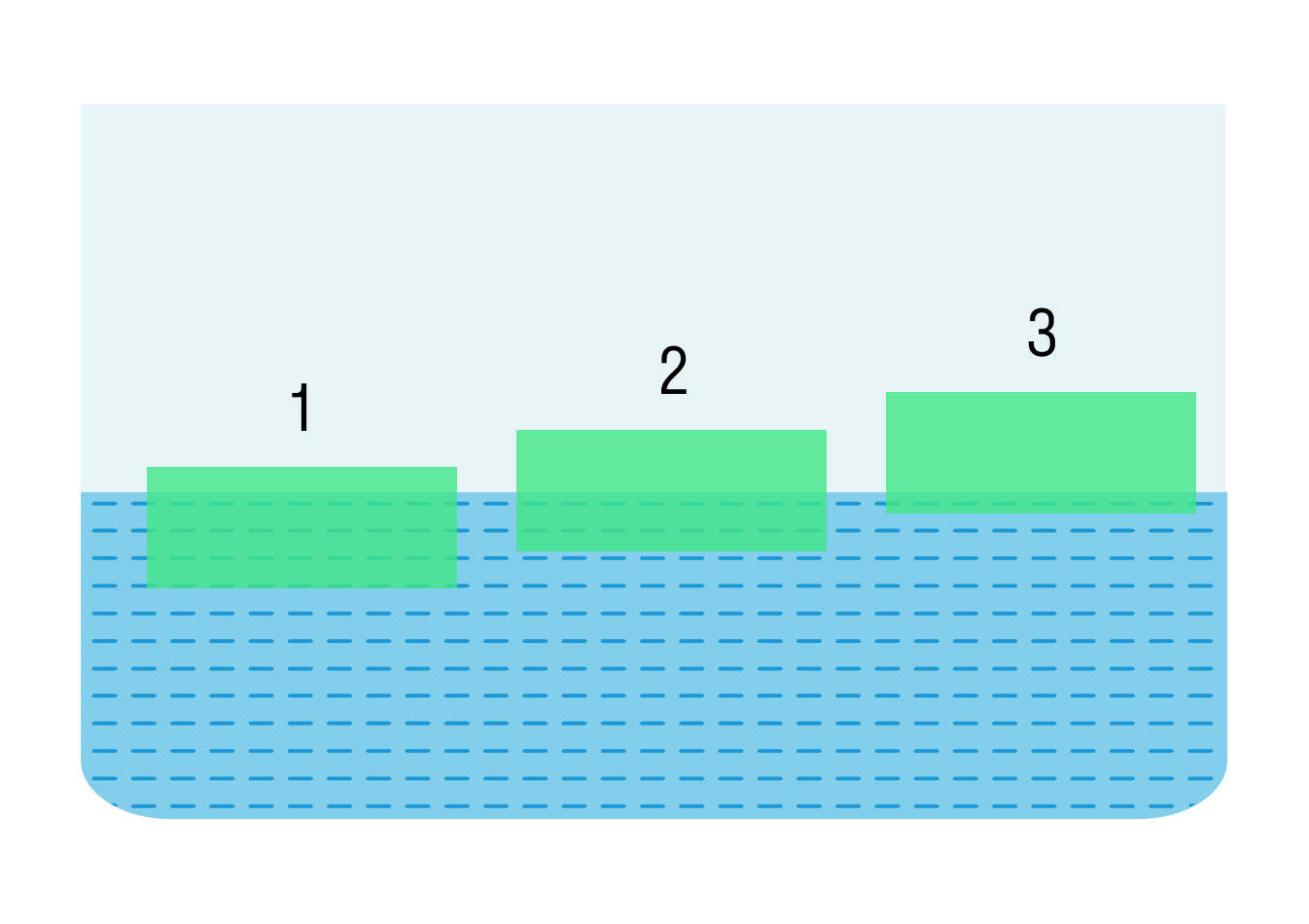
На поверхности воды плавают бруски из дерева, пробки и льда. Укажите, какой брусок из пробки, а какой изо льда? Какая существует зависимость между плотностью тела и объемом этого тела над водой?
Решение:
Чем меньше плотность тела, тем большая часть его находится над водой. Дерево плотнее пробки, а лед плотнее дерева. Значит изо льда — материал №1, а из пробки — №3.
Задача 3
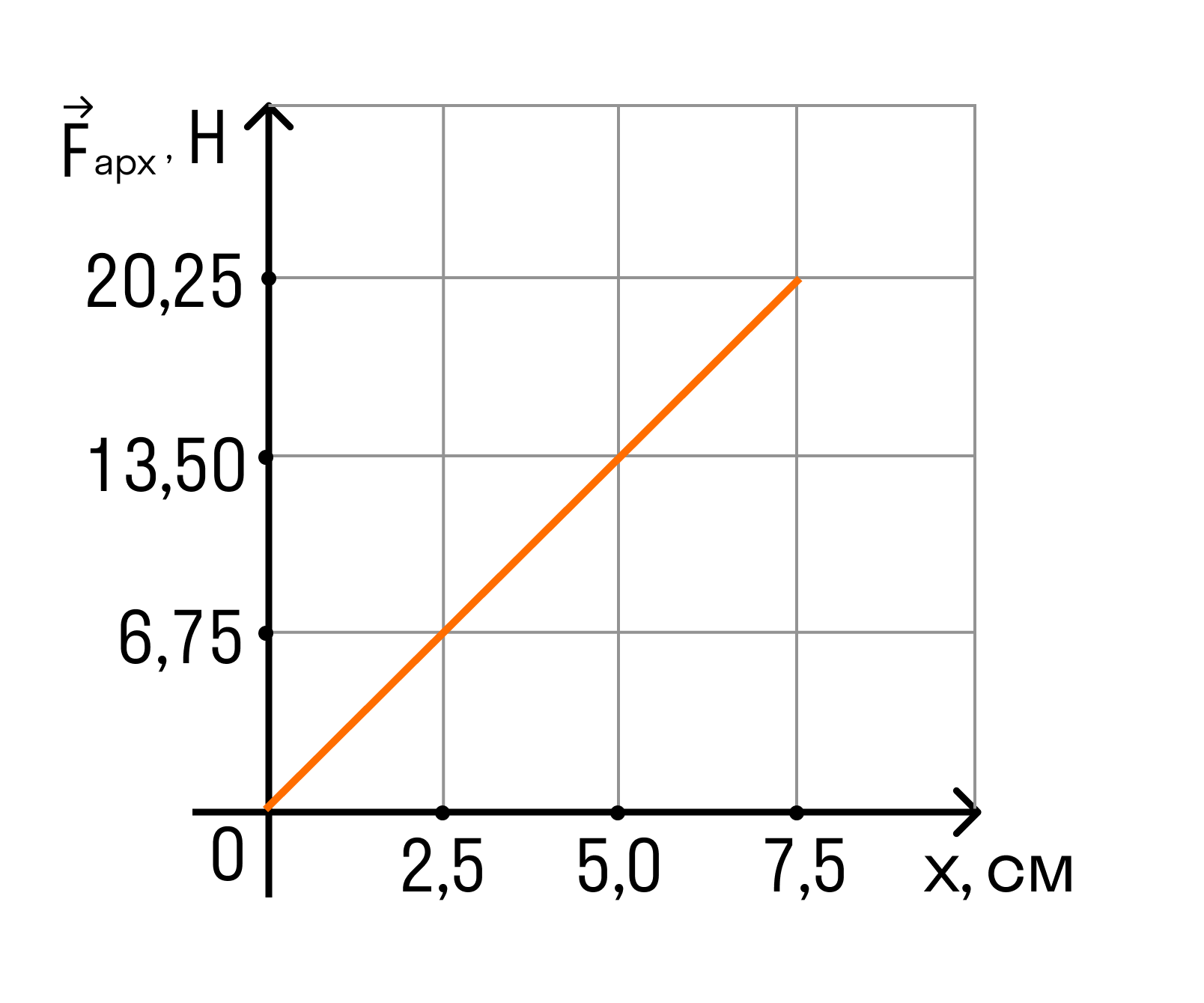
На графике показана зависимость модуля силы Архимеда FАрх, действующей на медленно погружаемый в жидкость кубик, от глубины погружения x. Длина ребра кубика равна 10 см, его нижнее основание всё время параллельно поверхности жидкости. Определите плотность жидкости. Ускорение свободного падения принять равным 10 м/с 2 .
Решение:
Сила Архимеда, действующая на кубик равна FАрх = ρж * g * Vпогр
V — объём погруженной части кубика,
ρ — плотность жидкости.
Учитывая, что нижнее основание кубика всё время параллельно поверхности жидкости, можем записать:
а — длина стороны кубика.
ρ = FАрх / (g * a 2 * x)
Рассматривая любую точку данного графика, получим:
ρ = FАрх / (g * a 2 * x) = 20,25 / (10 * 7,5 * 10 -2 ) = 2700 кг/м3
Ответ: плотность жидкости равна 2700 кг/м 3
Задача 4
В сосуде с водой, не касаясь стенок и дна, плавает деревянный кубик с длиной ребра 20 см. Кубик вынимают из воды, заменяют половину его объёма на материал, плотность которого в 6 раз больше плотности древесины, и помещают получившийся составной кубик обратно в сосуд с водой. На сколько увеличится модуль силы Архимеда, действующей на кубик? (Плотность сосны — 400 кг/м 3 .)
Решение:
В первом случае кубик плавает в воде, а это значит, что сила тяжести уравновешивается силой Архимеда:
FАрх1 = mg = ρт * g * a 3 = 400 * 0,2 3 * 10 = 32 Н
После замены части кубика его средняя плотность станет равной
0,5 * 400 + 0,5 * 2400 = 1400 кг/м 3
Получившаяся плотность больше плотности воды = 100 кг/м 3 . Это значит, что во втором случае кубик полностью погрузится в воду. Сила Архимеда в этом случае будет равна:
FАрх2 = ρт * g * Vт = 1000 * 10 * 0,23 = 80 Н
Отсюда получаем, что сила Архимеда увеличится на 48 Н.
Ответ: сила Архимеда увеличится 48 Н
Курсы подготовки к ОГЭ по физике помогут снять стресс перед экзаменом и получить высокий балл.
Видео:Урок 2. Уравнение состояния идеального газа. Теория. База. ЕГЭСкачать

Плавание тел
Из закона Архимеда есть следствия об условиях плавания тел.
Условия плавания тел
Плавание внутри жидкости
Плавание на поверхности жидкости
Если плотность тела меньше плотности жидкости или газа — оно будет плавать на поверхности.
Почему корабли не тонут?
Корабль сделан из металла, плотность которого больше плотности воды. И, по идее, он должен тонуть. Но дело в том, что корпус корабля заполнен воздухом, поэтому общая плотность судна оказывается меньше плотности воды, и сила Архимеда выталкивает его на поверхность. Если корабль получит пробоину, то пространство внутри заполнится водой — следовательно, общая плотность корабля увеличится. Судно утонет.
В подводных лодках есть специальные резервуары, заполняемые водой или сжатым воздухом. Если нужно уйти на глубину — водой, если подняться — сжатым воздухом. Рыбы используют такой же принцип в плавательном пузыре — наполняют его воздухом, чтобы подняться наверх.
Человеку, чтобы не утонуть, тоже достаточно набрать в легкие воздух и не двигаться — вода будет выталкивать тело на поверхность. Именно поэтому важно не тратить силы и кислород в легких на панику и борьбу, а расслабиться и позволить физическим законам сделать все за нас.
🎦 Видео
10 класс урок №39 Уравнение состояния идеального газаСкачать

Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Уравнение состояния идеального газа. Изопроцессы.Закон ДальтонаСкачать