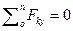Уравнения равновесия (статики) характеризуют неподвижность заданной системы нагруженной комплексом внешних усилий.
При решении задач теоретической механики и сопротивления материалов (например, при определении опорных реакций или внутренних силовых факторов) исходя из условия неподвижности системы или ее частей, записываются уравнения равенства нулю сумм проекций всех сил на оси выбранной системы координат
что следует из условия отсутствия перемещения системы вдоль этих осей, и сумм моментов относительно произвольных точек системы
из условия отсутствия ее вращения относительно указанных осей.
Надо отметить что в случае действия плоской системы сил можно получить только три уравнения статики, а линейная схема нагружения позволяет записать лишь одно уравнение.
- Пример составления уравнений равновесия
- Суммы проекций сил
- Суммы моментов
- Равновесие пространственной системы сходящихся сил в теоретической механике
- Правило параллелепипеда сил
- Проекция силы на три взаимно перпендикулярные оси. Определение равнодействующей системы пространственных сил, приложенных к точке
- Равновесие пространственной системы сходящихся сил
- Момент силы относительно оси
- Равновесие произвольной пространственной системы сил
- Разновидности опор балочных систем
- 🔥 Видео
Видео:Определение реакций опор простой рамыСкачать

Пример составления уравнений равновесия
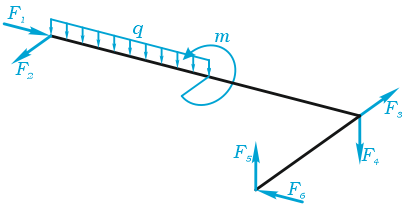
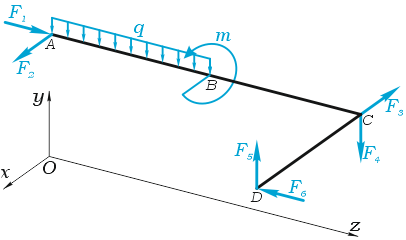
В качестве примера, рассмотрим общий случай пространственного нагружения, где комплекс усилий, включающий сосредоточенные силы F1-F6, равномерно распределенную нагрузку q, и момент m расположенный в плоскости перпендикулярной длинному стержню, удерживает L-образную систему в равновесии.
Обозначим характерные точки системы буквами A, B, C и D, зададим положение трехмерной системы координат xyz и запишем уравнения равновесия.
Суммы проекций сил
Сумма проекций всех сил на ось x (с учетом правила знаков для сил):
здесь при записи силы от распределенной нагрузки ее интенсивность q умножается на ее длину AB.
Суммы моментов
Суммы моментов всех нагрузок, например, относительно точки B (с учетом правила знаков для моментов):
- в плоскости xOy:
- в плоскости xOz:
- в плоскости yOz:
Из полученных шести уравнений можно определить не более шести неизвестных усилий.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Видео:Статика. Условия равновесия плоской системы сил (23)Скачать

Равновесие пространственной системы сходящихся сил в теоретической механике
Пространственная система сил:
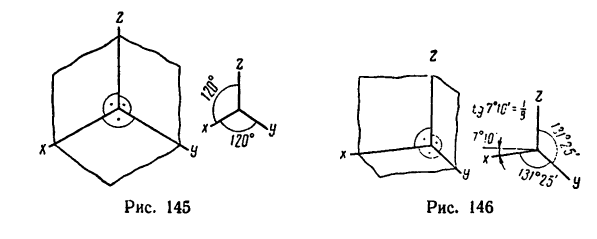
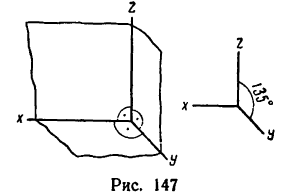
При решении задач, приведенных в этой главе, необходимо использовать не две оси координат, которые всегда можно расположить в одной плоскости —в плоскости рисунка, иллюстрирующего задачу, а три взаимно перпендикулярные оси.
Эти оси нельзя расположить в одной плоскости и при изображении пространственной системы сил на рисунке надо использовать одну из принятых в машиностроительном черчении аксонометриейческих проекций (ГОСТ 2.305—68. Изображения — виды, разрезы, сечения).
На рис. 145 показано изображение трех взаимно перпендикулярных плоскостей в изометрической проекции. Пересечение двух вертикальных плоскостей определяет положение вертикальной оси z,
пересечением обеих вертикальных плоскостей с горизонтальной определяются положения двух горизонтальных осей х и у.
На рис. 146 представлены те же три взаимно перпендикулярные плоскости в диметрической проекции, а на рис. 147—в фронтальной диметрической проекции. На каждом рисунке справа показано положение осей при изображении соответствующей проекции.
Если при решении задач, в которых рассматривается пространственная система сил, трудно представить взаимное расположение сил или их расположение относительно выбранных осей координат, то следует изготовить из плотной бумаги модель трех пересекающихся под прямым углом плоскостей, а линии пересечения плоскостей выделить цветными линиями и обозначить их соответственно х, у и z, В такой модели трех взаимно перпендикулярных осей можно помещать модели систем сил, рассматриваемых в задаче, изготовленные из пластилина, проволочек и спичек.
Видео:Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать

Правило параллелепипеда сил
Простейшую пространственную систему сходящихся сил образуют три силы, приложенные к одной точке.
Для сложения таких трех сил применяется правило параллелепипеда (рис. 148). Если даны силы 
В частном случае, который наиболее характерен для решения практических задач, три данные силы 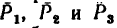
В этом случае модуль равнодействующей
а направление R относительно каждой из составляющих сил можно найти по формулам
Так же как и правило параллелограмма (см. § 1-1, 5-2 и 6-2), правило параллелепипеда можно использовать не только при сложении сил, но и при разложении данной силы на три составляющие. Наиболее часто производят разложение силы на составляющие, действующие по трем взаимно перпендикулярным направлениям.
Задача №
Три цепи одинаковой длины l соединены вместе кольцом А (рис. 150, о). Оставшиеся свободными концы цепей закреплены в трех точках В, С и D таким образом, что эти точки образуют вершины куба. Как необходимо установить под кольцо А подпорку АЕ и какую длину она должна иметь, чтобы кольцо А располагалось относительно точек В, С и D как четвертая вершина куба? При этом цепь АВ должна быть натянута силой Р, а цепи AD и ИС—силами 2Р каждая. Определить также усилие в подпорке АЕ. Весом подпорки пренебречь.
1. Из точки А (рис. 150, б) вдоль цепей отложим заданные силы: вдоль цепи АВ — силу Р, вдоль цепей АС и AD — силы 2Р. Построив на них параллелепипед, получим в нем диагональ ААХ, выражающую равнодействующую трех усилий в цепях.
Вдоль линии действия равнодействующей R нужно установить подпорку АЕ, которая должна соответствовать диагонали параллелепипеда 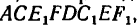
2. Находим модуль равнодействующей:
3. Из подобия двух показанных на рис. 150, б параллелепипедов следует пропорция
Зная, что длина цепи АС — 1, находим длину подпорки АЕ:
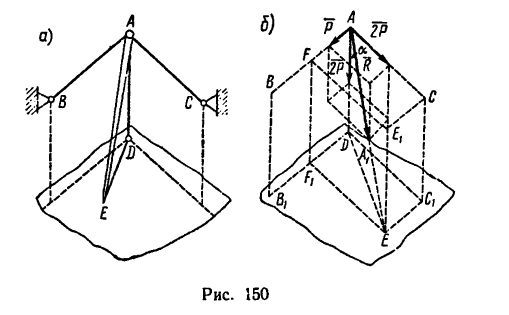
а также расстояние 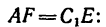
Таким образом, усилие в подпорке равно 3Р, длина подпорки 1,5l, а установить ее нужно так, чтобы нижний конец Е находился
от 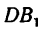
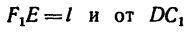
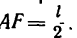
Решение этой задачи после выполнения пункта 2 можно продолжать иным путем. Можно найти угол а, образуемый 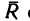

Задача №
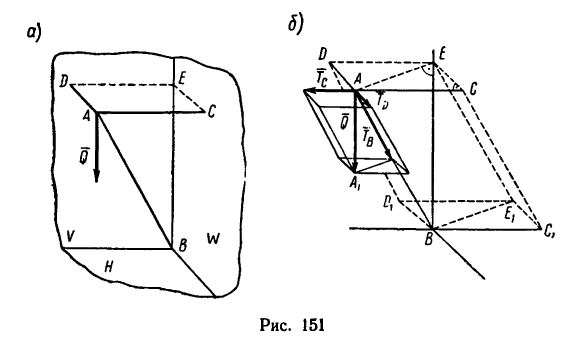
Найти усилия в стержне АВ и цепях АС и AD, поддерживающих груз Q весом 42 кГ, если AВ = 145сл, AС=80сл, AD = 60 см. Плоскость прямоугольника CADE горизонтальна, а плоскости V п W вертикальны. Крепление в точке В шарнирное (рис. 151, а).
1. Разложим силу Q на три составляющие 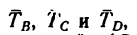
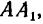
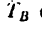
стержень АВ, а составляющие 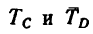
2. Соответственно приняв отрезок BE за диагональ, а стержень АВ и цепи АС и AD—за ребра, построим параллелепипед, подобный силовому (см. рис. 151, б).
3. Из подобия параллелепипедов, полученных на рис. 151, б, следует пропорция
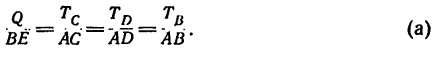
4. Длины трех отрезков из четырех, входящих в пропорцию, известны. Длина отрезка BE неизвестна. Найдем ее из рассмотрения прямоугольных треугольников АВЕ и АСЕ:
5. Рассматривая теперь первое отношение пропорции (а) вместе со вторым, а затем с третьим и четвертым, находим
Проекция силы на три взаимно перпендикулярные оси. Определение равнодействующей системы пространственных сил, приложенных к точке
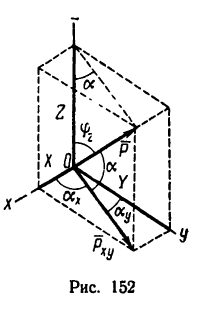
Если требуется определить проекции силы 
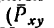
Легко заметить, что на трех взаимно перпендикулярных проекциях можно построить прямоугольный параллелепипед, диагональю которого является проектируемый вектор.
Из рис. 152 видно, что проекция на горизонтальную плоскость
поэтому 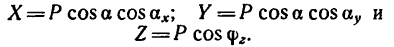
Если же известны углы 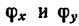
При помощи проекций сил на три оси легко определить равнодействующую системы сил, приложенных к точке.
Для этого необходимо:
1) выбрать расположение осей так, чтобы проекции всех сил определились простейшим образом;
2) найти проекции всех сил на каждую из осей;
3) сложить проекции всех сил на каждую из осей и найти таким образом три проекции искомой равнодействующей на оси:
4) определить модуль равнодействующей Р:
5) определить направление равнодействующей, найдя какие-либо два угла из трех:
Задача №
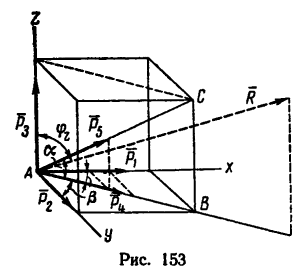
На одну из вершин куба действуют пять сил таким образом, что три силы направлены вдоль ребер, сходящихся в этой вершине; четвертая сила направлена по диагонали грани, а пятая—вдоль диагонали самого куба. Определить равнодействующую.
1. Приняв точку А за вершину куба, изобразим данные силы. Силы 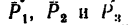
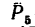
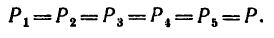
2. Ось х совместим с ребром куба, вдоль которого действует сила 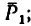
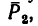
3. Найдем проекции сил на каждую из осей: 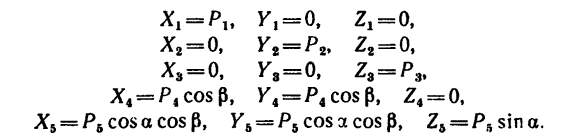
4. Сложим проекции на каждую ось и найдем проекции равнодействующей, учитывая, что модули всех сил равны между собой
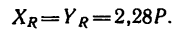
Равенство проекций получается из-за симметричности расположения сил относительно диагональной плоскости куба (плоскости, в которой расположен 
5. Определим модуль равнодействующей:
6. Так как силы расположены симметрично относительно диагональной плоскости куба, линия действия равнодействующей находится в плоскости симметрии расположения сил, проходящей через ось z. Поэтому направление равнодействующей определяется углом 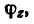
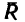
чему соответствует угол
На рис. 153 положение равнодействующей показано штриховым вектором
Равновесие пространственной системы сходящихся сил
Если система сходящихся сил уравновешена, то ее равнодействующая R = 0, а это означает, что и проекции равнодействующей на.три взаимно перпендикулярные оси равны нулю 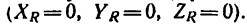
При помощи этих уравнений и решаются задачи на равновесие пространственной системы сходящихся сил.
Уравнений равновесия —три, следовательно, статически определимой является такая пространственная система сходящихся сил, в которой неизвестных сил не более трех.
Задача №
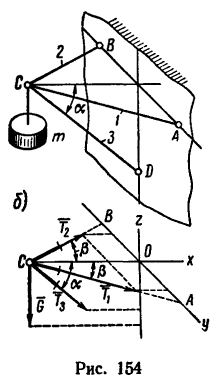
Груз, масса которого m= 500 кГ, подвешен на кронштейне ABCD, состоящем из трех стержней 1,2 и 3. Стержни 1 и 2 образуют в месте соединения прямой угол и расположены в горизонтальной плоскости. Стержень 3 образует с горизонтальной плоскостью угол а = 40° (рис. 154, а). Определить усилия, вызванные действием груза в стержнях. Соединения стержней между собой и с вертикальной стенкой шарнирные. Весом стержней пренебречь.
1. Решаем задачу в единицах системы СИ. На точку С кронштейна действует вертикальная нагрузка, равная весу массы груза, поэтому
2. Действие веса G на кронштейн уравновешивается реакциями трех стержней. Известно, что реакции направлены вдоль стержней (так как соединения стержней шарнирные). Нужно определить их модули и направление каждой реакции, т. е. определить, какой из стержней сжат, а какой растянут.
Мысленно разрежем стержни вблизи точки С и изобразим узел С, образуемый соединением трех стержней отдельно (рис. 154, б) вместе с четырьмя действующими на него силами: вертикально вниз действует известная сила G = 4,9 кн, а вдоль стержней действуют три их реакции: 
3. Расположим оси координат, как показано на рисунке. Замечая, что осью х прямой угол АСВ разделен пополам
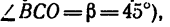
4 Решаем полученную систему уравнений. Из уравнения (3) 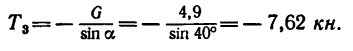
Знак «минус» показывает, что реакция 
Из уравнения (I) 
Числовые значения реакций 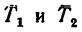
5. Если найденные значения реакций стержней перевести в единицы технической системы, то
Правильность перевода из единиц системы СИ в единицы технической системы рекомендуется проверить самостоятельно.
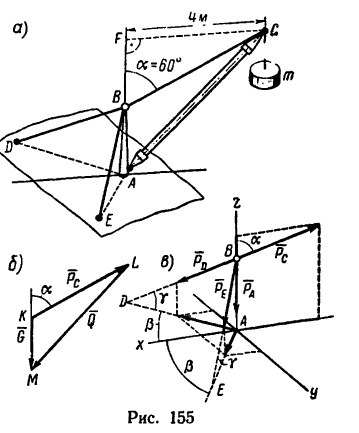
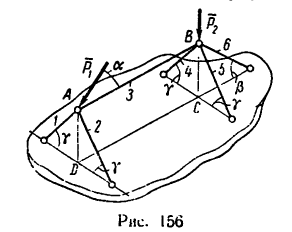
Задача №
Переносный кран, поднимающий груз массой m = 2000/кг, устроен так, как указано на рис. 155, a; AB = AD = АЕ=2м; угол DAE —120″, плоскость АВС, в которой расположена стрела АС крана, делит двугранный угол DAE пополам.
Определить силу, сжимающую вертикальную стойку АВ, и силы, растягивающие тросы BD и BF весом частей крана пренебречь.
1. В задаче рассматривается равновесие системы тел—стрелы и стойки, связанных струной ВС. Прежде чем приступить к определению усилий в стойке и тросах, необходимо найти натяжение струны ВС.
2. В точке С на кран действует вес 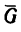
Разложим вес G на две составляющие, действующие вдоль струны ВС и стрелы АС, воспользовавшись правилом треугольника (рис. 155, б). Для этого из произвольной точки К построим вектор G, а затем из его начала и конца проведем линии, параллельные ВС и АС. В получившемся силовом треугольнике KLM (KL || ВС и LM|| СА) сторона KL изображает силу 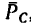
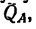
Из построения следует, что
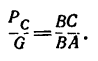
Отсюда 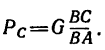
Не известную по условию задачи длину струны ВС легко найти, рассмотрев прямоугольный треугольник BCF (см. рис. 155, а)
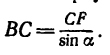
Таким образом, 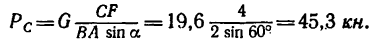
3. Перенесем силу 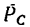
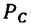
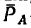
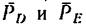
4. Расположим систему координатных осей, как показано на рис. 155, в и составим три уравнения равновесия:
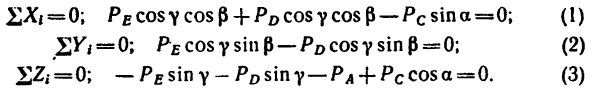
Замечая, что y = 45° (так как треугольники ВАЕ и BAD имеют равные катеты: BA=AE — AD) и а = 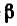
Теперь уравнения (1) и (3) примут такой вид:
Умножим обе части уравнения (5) на cos 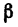
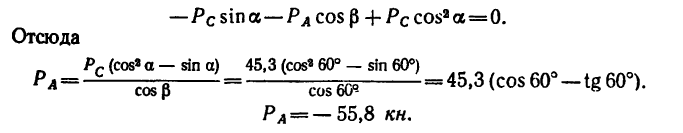
Знак «минус» указывает на то, что реакция 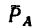
Подставив найденное значение 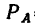
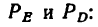
Отсюда 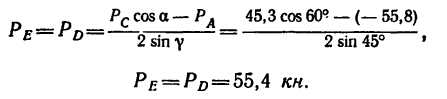
Тросы AD и AE растянуты усилиями по 55,4 кн.
Следующую задачу рекомендуется решить самостоятельно.
Момент силы относительно оси
Чтобы определить момент силы 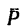
- 1) расположить плоскость Н перпендикулярно оси z;
- 2) определить проекцию силы Р на плоскость H — найти
- 3) из точки пересечения о.си с плоскостью (из точки О) провести перпендикуляр к направлению проекции
этого перпендикуляра О А — плечо силы
- 4) определить знак момента, придерживаясь такого правила: посмотрим на плоскость H со стороны положительного направления оси, если увидим, что проекция
поворачивает плечо против хода часовой стрелки, значит момент имеет положительный знак; а если проекция
поворачивает плечо по часовой стрелке (как это показано, например, на рис. 157), момент имеет отрицательный знак;
- 5) находим числовое значение момента силы Р относительно оси; для этого
—модуль проекции силы Р на плоскость, перпендикулярную к оси, умножаем на плечо О А.
Таким образом (см. рис. 157) 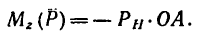
Момент силы относительно оси, так же как и момент силы относительно точки, измеряется по Международной системе (СИ) в ньютон-метрах (н м) или в килоньютон-метрах (н-м), а по технической системе
Для успешного решения задач и облегчения составления уравнений моментов относительно осей нужно иметь в виду три частных случая, в которых момент силы относительно оси равен нулю (рис. 158):
Случай 1-й (рис. 158, а). Сила Р или линия ее действия пересекает ось; в этом случае плечо О А — 0, поэтому
Случай 2-й (рис. 158, б). Линия действия силы 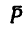
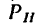
Случай 3-й (рис. 158, в). Линия действия силы Р совпадает с осью; в этом случае и 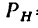
Задача №
К вершинам квадрата ABCD (AB = AD = 2 м), расположенного в горизонтальной плоскости, приложены силы 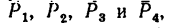
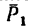
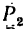
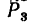
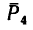
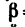
Модули сил
1. Замечаем, что расположение осей, показанное на рис. 159, определяет положение трех взаимно перпендикулярных плоскостей; плоскости , перпендикулярной к оси у, плоскости II, перпендикулярной к оси г, и плоскости III, перпендикулярной к оси х.
2. Определяем моменты силы 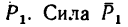
3. Определяем моменты силы
Сила 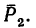
Чтобы определить момент силы 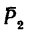
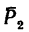
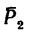
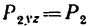
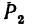
4. Определяем моменты силы
Сила 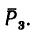
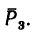
Плоскость, в которой расположена сила 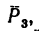
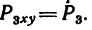
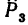
Знак момента положительный (если посмотреть на плоскость II со стороны оси z). Поэтому
5. Определяем моменты силы
Линия действия силы 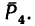
Спроектируем силы 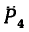
плечом силы 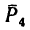
Равновесие произвольной пространственной системы сил
Произвольную пространственную систему сил, так же как и плоскую, можно привести к одной точке и заменить главным вектором 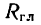
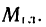
Если 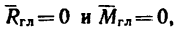
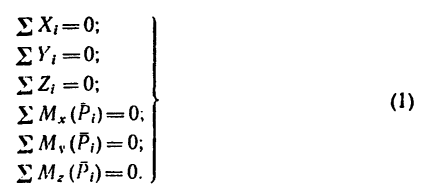
Первые три уравнения (уравнения проекций) получены из условия 
Последние три уравнения (уравнения моментов) получены из условия 
Для облегчения составления уравнений равновесия тело, равновесие которого рассматривается, целесообразно изображать вместе с действующими на него силами в проекциях на три основные
плоскости, т. е. изображать вид спереди, вид сверху и один боковой вид —вид слева или вид справа (см. задачи 115-22, 116-22 и 117-22).
В частном случае линии действия сил, образующих пространственную систему, могут оказаться параллельными. Тогда одну из осей (например, ось z) выгодно расположить параллельно силам (рис. 160), а две другие оси расположатся в плоскости, перпендикулярной к линиям действия сил.
Легко понять, что для уравновешенной пространственной системы параллельных сил вместо шести уравнений можно составить лишь три: алгебраическую сумму проекций сил на ось, параллельную данным силам, и два уравнения моментов относительно двух других осей. Остальные уравнения превратятся в тождество вида 0 = 0.
В соответствии с расположением осей (см. рис. 160) уравнения равновесия имеют вид:
Для пространственной системы параллельных сил можно составить лишь три уравнения равновесия, поэтому, чтобы задача была статически определимой, в ней должно содержаться не более трех неизвестных сил.
Задача 114-22. На рис. 161 схематично изображена трехколесная платформа для перевозки грузов. На платформе лежит груз Р = 8кн таким образом, что его вес можно считать приложенным в точке D, причем EO = DF = 0,1 м и DE = OF = 0,5 м.
Определить силы давления, производимые колесами на горизонтальную опорную плоскость.
Собственным весом платформы пренебречь.
1. Давления, производимые колесами, численно равны реакциям опоры, поэтому приложим к каждому колесу перпендикулярно к опорной плоскости реакции 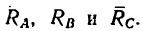
2. Расположим оси координат, как показано на рис. 161, и составим уравнения равновесия:
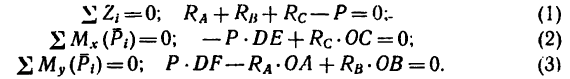
3. Решаем полученную систему уравнений. Из уравнения (2) 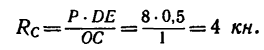
Затем решение можно продолжить так. Подставляя известные числовые значения в уравнения (1) и (3) и перенеся известные члены в правую сторону, получаем такую систему двух уравнений:
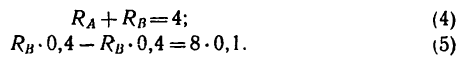
Разделим обе части уравнения (5) на 0,4, тогда система уравнений приобретает такой простой вид:
Сложив эти уравнения, найдем
Вычтем из первого второе, найдем
Как видно, реакции не равны между собой, следовательно, соответственно колеса давят на опорную плоскость также неодинаково.
Как нужно поместить груз Р, чтобы силы давления, производимые колесами, равнялись между собой?
В следующих задачах рассматриваются системы сил, произвольно расположенные в пространстве.
Задача №
Квадратная крышка весом 400 н удерживается приоткрытой на 60э над горизонтальной плоскостью противовесом Q (рис. 162). Определить, пренебрегая трением на блоке D,
вес противовеса Q и реакции шарниров А и В, если блок D укреплен на одной вертикали с шарниром А и AD=AC.
1. Выбрав за начало координат точку А и расположив оси так, как показано на рис. 162, покажем на этом же рисунке активные силы и реакции опор.
На крышку действует сила тяжести G, которую считаем приложенной в точке Е (центр симметрии квадрата), и реакция 
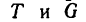
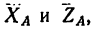
2. Если составление уравнений равновесия по рис. 162 затруднительно, можно предварительно изобразить крышку вместе с действующими на нее силами в трех проекциях, как это сделано на рис. 163:
а) вид спереди, ось х перпендикулярна к плоскости проекции;
б) вид сверху, ось г перпендикулярна к плоскости проекции;
в) вид слева, ось у перпендикулярна к плоскости проекции.
3. Составим уравнения равновесия.
Для составления уравнений проекций на ось х воспользуемся рис. 163, б или 163, в:
На ось у силы не проектируются, так как все они перпендикулярны к этой оси.
Для составления уравнений проекций на ось z воспользуемся рис. 163, а или 163, в:
Для составления уравнения моментов относительно оси х воспользуемся рис. 163, а:
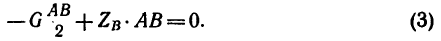
Для составления уравнения моментов относительно оси у воспользуемся рис. 163, в:
Для составления уравнения моментов относительно оси г воспользуемся рис. 163, б:

4. Решаем полученные уравнения.
Из уравнения (5) находим (так как 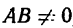
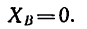
Из уравнения (4)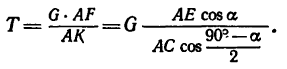
Так как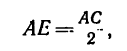
то
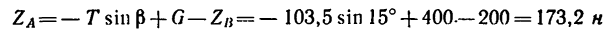
(угол 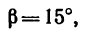
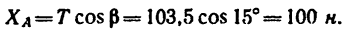
Таким образом, чтобы крышка находилась в равновесии приоткрытой под углом 60°, вес противовеса должен быть Q = T = 103,5 н. При этом реакция шарнира А имеет две составляющие: горизонтальную 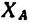
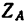
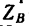
Задача №
На вал 1 ворота намотана веревка, удерживающая груз Q (рис. 164). Радиус колеса 2 ворота в четыре раза больше радиуса вала. Веревка, прикрепленная к ободу колеса и натягиваемая грузом силой Р =80 н, сходит с колеса в точке F по касательной; радиус DF колеса образует с вертикалью угол а=60и. Определить величину груза Q, при котором ворот остается в равновесии, а также реакции подшипников А и В, если общий вес вала и колеса G = 600 н и приложен в точке С (АС = 0,4 м).
1. Три нагрузки-вес 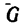
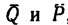
действуют в плоскостях, перпендикулярных к оси вала, и, следовательно, не смещают вал вдоль оси, поэтому и реакции подшипников расположатся в плоскостях, перпендикулярных к этой же оси. Заменим их составляющими 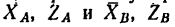
Следует учесть, что обычный подшипник не создает реакции, направленной вдоль оси вала. Нели на вал действуют нагрузки, смещающие вал вдоль оси, то один из подшипников должен быть заменен подпятником.
2. Изобразим ворот со всеми действующими на него силами в трех проекциях (рис. 165 а, б, в) и при помощи их составим уравнения равновесия.
Так же как и в предыдущей задаче, уравнение проекций на ось у превратится в тождество вида 0 = 0. При составлении уравнения моментов относительно оси у- уравнения (4)—нужно учитывать, что радиус колеса R в четыре раза больше радиуса вала 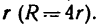
3. Из уравнения (5)
3. Из уравнения (5)
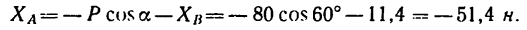
Задача 117-22. Деревянный брус прямоугольного поперечного сечения b= 20 см и h= 25 см жестко заделан в стене таким образом, что выступающая из стены часть бруса горизонтальна и имеет длину 
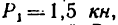
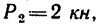
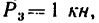
Определить реакции заделки.
1. Освободим брус от связи (от стены) и заменим ее реакциями (рис. 166, б). Как известно, равновесие балки, жестко заделанной одним концом, обеспечивается двумя реактивными факторами: реактивной силой и реактивным моментом. В данной задаче нагрузки, действующие
на брус, расположены не в одной плоскости, поэтому нельзя заранее определить, в каких плоскостях расположатся реактивная сила и реактивный момент.
Заменим реактивную силу тремя составляющими: 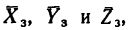
2. Таким образом, на брус, кроме трех заданных сил, действуют шесть неизвестных реактивных факторов три силы и три момента. Для пространственной системы сил можно составить шесть уравнений равновесия — значит задача статически определима.
* Как известно, пару сил можно тоже представить в виде вектора. Вектор пары сил, так же как и вектор силы, можно разложить на три составляющих вектора, направленных вдоль осей (рис. 167, а), а зачем каждый составляющий вектор пары заменить парой сил, действующей в плоскости, перпендикулярной к тон оси, вдоль которой направлен вектор нары (рис. 167 б, в, г).
3. Для облегчения составления уравнений равновесия изобразим брус вместе с действующими на него силами в трех проекциях (рис. 168, а) и составим уравнение равновесия.
Можно, конечно, при составлении уравнений пользоваться только одним рис. 166, б:
4. Решая эти уравнения, получаем:
- из (1)
- из (2)
- из (3)
- из (4)
- из (5)
- из (6)
Одной из типичных задач, в которых применяются уравнения равновесия пространственной системы сил, является задача определения реакций опор вала какой-либо машины.
Задачи этого типа можно решать так же, как задачи 115-22 или 116-22, т. е. при помощи проекций вала вместе с векторами заданных и искомых сил на три взаимно перпендикулярные плоскости. Но в некоторых случаях оказывается более рациональным несколько иной прием решения, основанный на приведении сил к оси вала. В качестве примера для такого решения возьмем вал одного из многочисленных видов редукторов *.
Задача №
На вале редуктора жестко укреплены два зубчатых колеса: коническое / и цилиндрическое 2 (рис. 169, а). Левая цапфа вала опирается на подшипник, воспринимающий только радиальную силу давления, действующую перпендикулярно к оси вала, а правая цапфа (пята) опирается на подпятник, т. е. на опору, способную, кроме радиальной силы давления, воспринимать и осевую (силу, действующую вдоль оси вала).
На колесо 1 действуют три силы: касательная 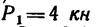
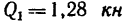
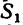
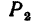
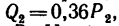
1. Заданные и искомые силы, приложенные к колесам 1 и 2, приведем к точкам 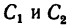
Сила 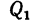
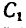
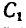
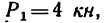
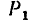
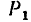
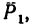
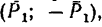
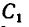
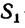
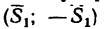
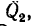
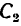
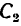
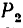

2. Освободив вал в точках A и В от опор, заменяем действие опор их реакциями: подшипник А нс препятствует горизонтальному смещению вала, поэтому его реакцию, расположенную в плоскости, перпендикулярной к оси вала, заменяем двумя составляющими: горизонтальной 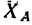
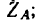
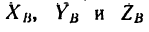
• Редуктором называется механическое устройство для передачи мощности от двигателя, вал которого вращается с большой скоростью, к рабочей машине, вал которой имеет скорость вращения, в несколько раз меньшую.
3. При известном навыке решения задач вместо расчетной схемы, показанной на рис. 169, б, можно получить более простую схему (рис. 169, в), на которой вместо пар сил круговыми стрелками обозначены их моменты. Так, круговой стрелкой 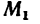

перпендикулярной к оси у; 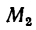
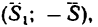
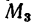
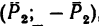
Если силы выражать в кн, а плечи пар в м, то получим такие абсолютные числовые значения моментов
а момент 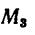
4. Составим шесть уравнений равновесия. 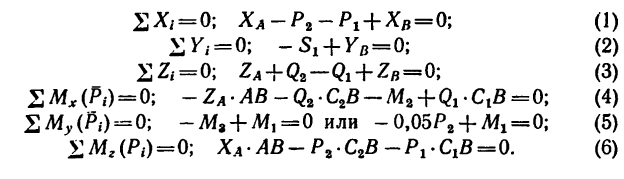
5. Решая эти уравнения последовательно, получим: из уравнения (5)
Так как
то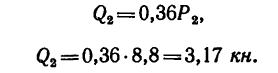
Из уравнения (6) 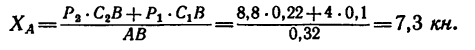
Из уравнения (4)
Реакция 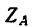
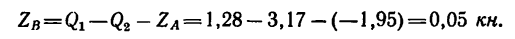
Из уравнения (2)
Из уравнения (1)
Следующие три задачи рекомендуется решить самостоятельно.
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Определение положения центра тяжести тела
- Равномерное прямолинейное движение точки
- Равномерное криволинейное движение точки
- Равнопеременное движение точки
- Определение равнодействующей сходящихся сил
- Равновесие сходящихся сил
- Равновесие трех непараллельных сил
- Сочлененные системы
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Графический способ определения равнодействующейСкачать

Разновидности опор балочных систем
Читайте также:
|
| < |  |
 | |
 |
Контрольные вопросы и задания
1. Замените распределенную нагрузку сосредоточенной и определите расстояние от точки приложения равнодействующей до опоры А (рис. 6.9).
2. Рассчитайте величину суммарного момента сил системы относительно точки А (рис. 6.10).
3. Какую из форм уравнений равновесия целесообразно использовать при определение реакций в заделке?
4. Какую форму системы уравнений равновесия целесообразно использовать при определении реакций в опорах двухопорной балки и почему?
5. Определить реактивный момент в заделке одноопорной балки, изображенной на схеме (рис. 6.11).
6. Определите вертикальную реакцию в заделке для балки, представленной на рис. 6.11.
Дата добавления: 2015-04-11 ; просмотров: 16 ; Нарушение авторских прав
🔥 Видео
1 Решение задачи графическим и аналитическим методомСкачать

Система сходящихся сил. Решение задач по МещерскомуСкачать

Определение реакций опор в балке. Сопромат.Скачать

Равновесие системы телСкачать

Произвольная плоская система сил. Задача 1Скачать

4.4 Аналитические уравнения равновесияСкачать

4.1 Плоская система сил. Графическое условие равновесия (решение задач)Скачать

Метод сил. Расчет стержневой системы с одной неизвестнойСкачать

Равновесие тел. Условие равновесия тел. Центр масс и центр тяжести. Практическая часть. 10 класс.Скачать

Статика. Теорема Пуансо. Лекция (20)Скачать

Химическое равновесие. Константа равновесия. 10 класс.Скачать

Как выучить Химию с нуля за 10 минут? Принцип Ле-ШательеСкачать

Геометрический способ определения равнодействующей силыСкачать

4.3 Формула определения равнодействующей силыСкачать

Задача о составной конструкцииСкачать

Статически неопределимые системы. Метод силСкачать


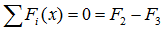
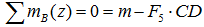
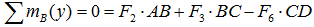
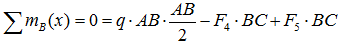
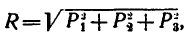
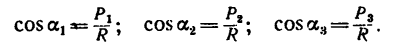
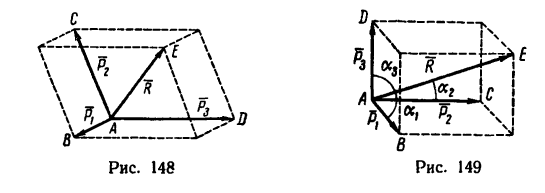
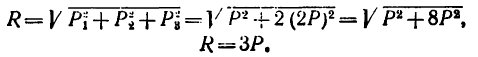
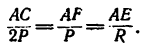
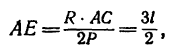
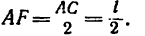
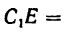
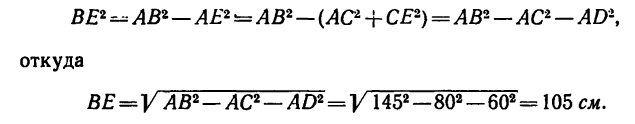
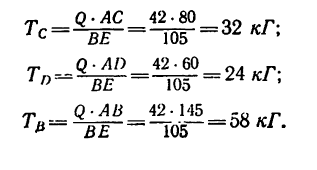
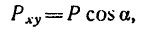
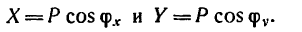
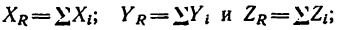
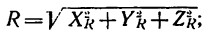
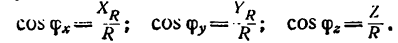
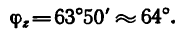
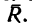
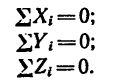
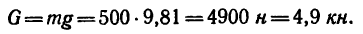
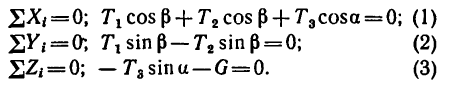
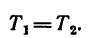
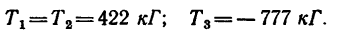
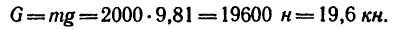
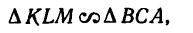
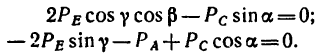
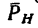 этого перпендикуляра О А — плечо силы
этого перпендикуляра О А — плечо силы 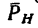
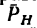 поворачивает плечо против хода часовой стрелки, значит момент имеет положительный знак; а если проекция
поворачивает плечо против хода часовой стрелки, значит момент имеет положительный знак; а если проекция 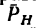 поворачивает плечо по часовой стрелке (как это показано, например, на рис. 157), момент имеет отрицательный знак;
поворачивает плечо по часовой стрелке (как это показано, например, на рис. 157), момент имеет отрицательный знак;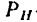 —модуль проекции силы Р на плоскость, перпендикулярную к оси, умножаем на плечо О А.
—модуль проекции силы Р на плоскость, перпендикулярную к оси, умножаем на плечо О А.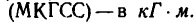
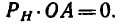
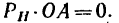
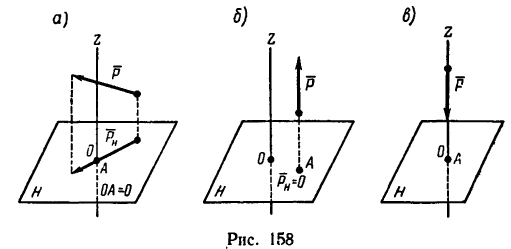
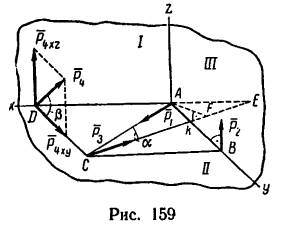
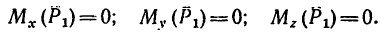
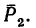
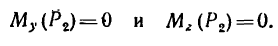
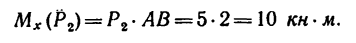
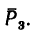
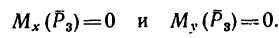
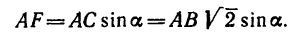
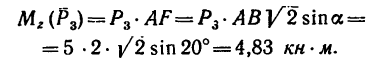
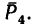
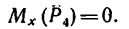
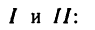
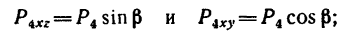
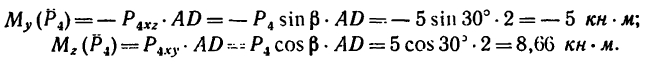
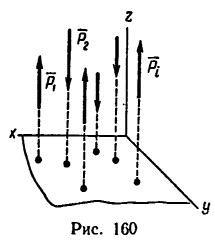

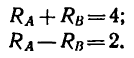
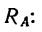
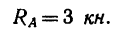
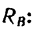
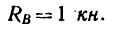
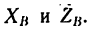
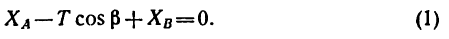
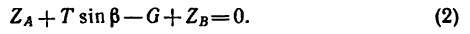
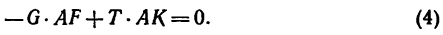
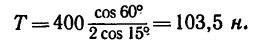
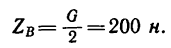
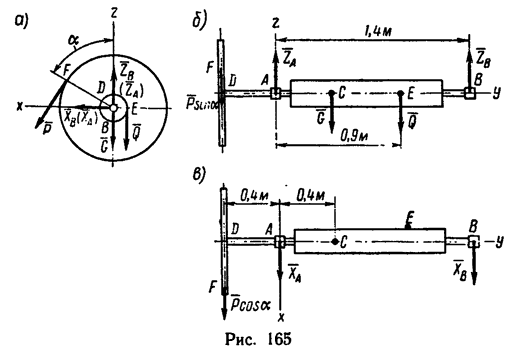
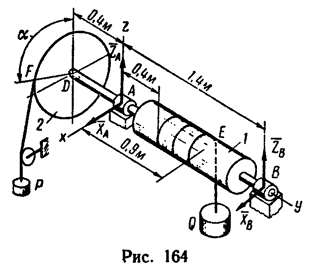
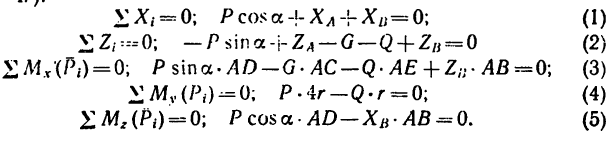
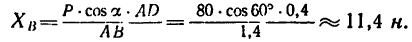
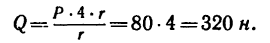
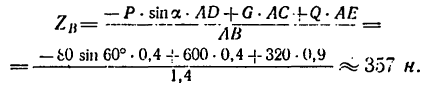
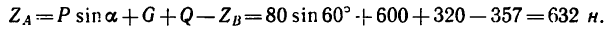
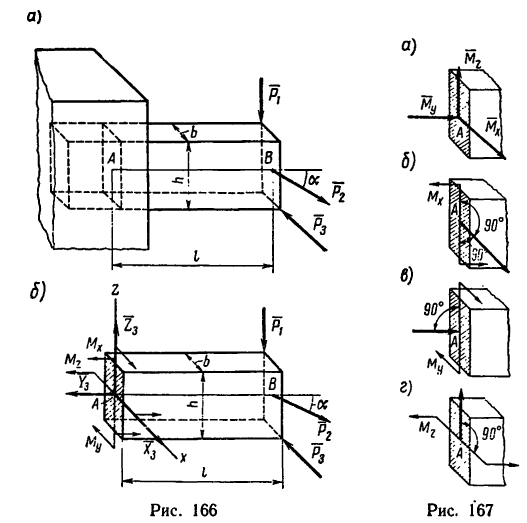
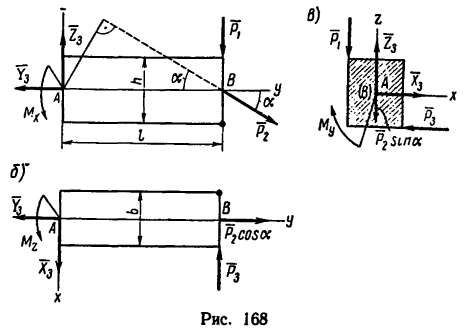
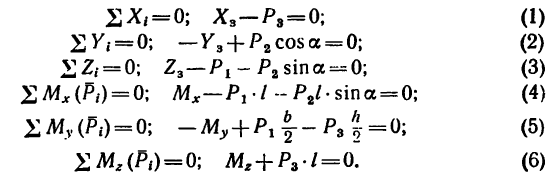
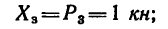
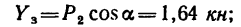
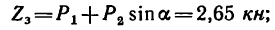
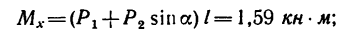
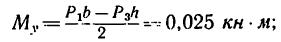
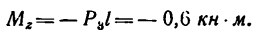
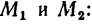
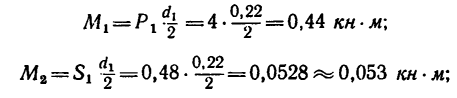
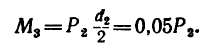
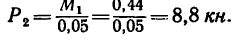

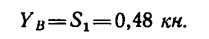
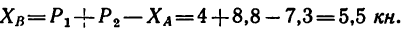




 Рис. 6.2
Рис. 6.2

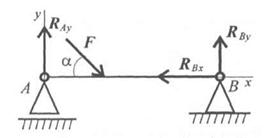

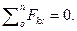
 определяется реакция RBx.
определяется реакция RBx. определяется реакция RBy.
определяется реакция RBy. определяется реакция RAy.
определяется реакция RAy.