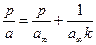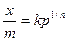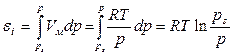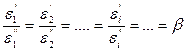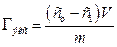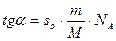Какие уравнения описывают зависимость поверхностного натяжения

Видео:Коэффициент поверхностного натяженияСкачать

Поверхностное натяжение

О чем эта статья:

Видео:Урок 197. Поверхностная энергия. Коэффициент поверхностного натяженияСкачать

Понятие и характеристики поверхностного натяжения

С явлением поверхностного натяжения жидкости мы сталкиваемся каждый день:

• капли воды стремятся принять форму, близкую к шарообразной (а в невесомости они совсем шарообразные);
• струя воды из-под крана стремится к цилиндрической форме;
• булавка не тонет на поверхности воды в стакане;
• многие насекомые могут скользить по поверхности воды.

Силы поверхностного натяжения действуют вдоль поверхности жидкости, стремясь сократить ее площадь. Как будто жидкость заключена в упругую пленку, которая стремится сжать свое содержимое.

Потенциальная энергия взаимного притяжения молекул жидкости примерно равна их кинетической энергии. Это позволяет веществу сохранять объем (но не форму), и этот объем ограничивается поверхностью жидкости.

На молекулу жидкости, которая находится внутри, действуют силы притяжения со стороны других молекул, и они уравновешивают друг друга. А на ту молекулу, что находится на поверхности, действуют силы притяжения не только со стороны других молекул жидкости, но и со стороны газа (внешней среды). Эти вторые значительно меньше первых, поэтому равнодействующая сила притяжения направлена внутрь жидкости, что способствует удержанию молекулы на поверхности.

Поверхностное натяжение — это величина, которая показывает стремление жидкости сократить свою свободную поверхность, то есть уменьшить избыток своей потенциальной энергии на границе раздела с газообразной фазой.

Чем больше площадь поверхности жидкости, тем больше молекул, которые обладают избыточной потенциальной энергией, и тем больше поверхностная энергия. Этот факт можно записать в виде следующего соотношения:

Поверхностная энергия жидкости

W = σS

W — поверхностная энергия жидкости [Дж]

S — площадь свободной поверхности [м 2 ]

σ — коэффициент поверхностного натяжения [Н/м]

Отсюда мы можем вывести формулу коэффициента поверхностного натяжения.

Коэффициент поверхностного натяжения — это физическая величина, которая характеризует данную жидкость и численно равна отношению поверхностной энергии к площади свободной поверхности жидкости.

Коэффициент поверхностного натяжения

σ = W/S

W — поверхностная энергия жидкости [Дж]

S — площадь свободной поверхности [м 2 ]

σ — коэффициент поверхностного натяжения [Н/м]

Коэффициент поверхностного натяжения жидкости зависит:

• от природы жидкости;
• температуры жидкости;
• свойств газа, который граничит с данной жидкостью;
• наличия поверхностно-активных веществ (например, мыло или стиральный порошок), которые уменьшают поверхностное натяжение.

Коэффициент поверхностного натяжения не зависит от площади свободной поверхности жидкости, хотя может быть рассчитан с ее помощью.

Если на жидкость не действуют другие силы или их действие мало, жидкость будет стремиться принимать форму сферы, как капля воды или мыльный пузырь. Так же ведет себя вода в невесомости. Жидкость ведет себя так, как будто по касательной к ее поверхности действуют силы, стягивающие эту поверхность. Эти силы называются силами поверхностного натяжения.

Сила поверхностного натяжения

F = σl

F — сила поверхностного натяжения [Н]

l — длина контура, ограничивающего поверхность жидкости [м]

σ — коэффициент поверхностного натяжения [Н/м]

В химической промышленности в воду часто добавляют специальные реагенты-смачиватели, не дающие ей собираться в капли на какой-либо поверхности. Например, их добавляют в жидкие средства для посудомоечных машин. Попадая в поверхностный слой воды, молекулы таких реагентов заметно ослабляют силы поверхностного натяжения, вода не собирается в капли и не оставляет на поверхности пятен после высыхания.

Видео:Поверхностное натяжениеСкачать

Какое уравнение описывает зависимость поверхностного натяжения водных растворов ПАВ от их концентрации?

Как уже отмечалось выше, основным для изучения адсорбции водорастворимых ПАВ на границе раздела вода-воздух является метод измерения зависимости поверхностного натяжения раствора ПАВ от его концентрации. Построение изотермы поверхностного натяжения позволяет перейти впоследствии к искомой изотерме адсорбции.

Б. Шишковский, исследуя зависимость поверхностного натяжения водных растворов гомологов карбоновых кислот от их концентрации, получил эмпирическое уравнение, которое на современном этапе развития коллоидной химии имеет следующий вид:

– уравнение Шишковского,

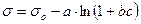
где σ – поверхностное натяжение раствора, σ_о – поверхностное натяжение воды, с – равновесная концентрация ПАВ, a и b – эмпирические константы.

Впоследствии было обнаружено, что такая зависимость справедлива не только для карбоновых кислот, но и для других растворимых в воде органических ПАВ (спирты, амины, альдегиды, сульфокислоты и др.).

Параметр a в уравнении Шишковского совпадает для всех членов гомологического ряда некоторых классов дифильных органических соединений, обладающих поверхностно-активными свойствами.

Константа b отличается для членов одного гомологического ряда, и в его пределах ее значение увеличивается в 3-3,5 раза при переходе к каждому следующему гомологу. Отметим, что указанная закономерность была уже установлена ранее и известна как правило Дюкло-Траубе.

Вопросы и задания для самоконтроля знаний по материалу 10-й лекции

1 Какие процессы, происходящие на границе конденсированных фаз с воздухом, могут вызывать понижение энергии гетерогенной системы?

2 Чем отличается хемосорбция от физической адсорбции?

3 Какие величины используются для количественного описания адсорбции?

4 Получите уравнение, связывающее полную адсорбцию с гиббсовской.

5 Что Вы знаете о классификации ПАВ?

6 Что такое изотерма поверхностного натяжения?

7 Какие уравнения, характеризующие адсорбцию, Вы знаете?

8 Что такое поверхностная активность? Как ее определяют по экспериментальным данным?

9 Что такое работа адсорбции?

10 Как определить параметры молекул ПАВ?

11 Взаимосвязь между какими характеристиками поверхностного слоя устанавливает уравнение Шишковского?

Знакомимся с основными понятиями физической химии (для курсантов военного факультета)

Повторяем курс физической химии (для студентов химического факультета)

ЛЕКЦИЯ 11

«По некоторым версиям причиной болезни И. Ньютона и Наполеона Бонапарта явились адсорбция в одном случае паров ртути, которые были обнаружены в волосах великого ученого (до болезни Ньютон 18 лет работал с ртутью), а во втором – паров мышьяка (в обоях спальни Наполеона обнаружили арсенид мышьяка)»

Поглощение паров древесным углем было впервые описано К. Шееле в 1773 г и аббатом Ф. Фонтана в 1777 г. Первое систематическое изучение адсорбции было проведено Т. Сосюром, исследовавшим поглощение различных газов некоторыми адсорбентами. К настоящему времени известны многочисленные области практического применения адсорбции, среди которых важнейшими являются: очистка газов от примесей (например, очистка аммиака перед его контактным окислением, очистка воздуха в подводных лодках и противогазах); извлечение и рекуперация веществ (например, извлечение газолина из природного газа, рекуперация паров летучих растворителей в производстве полимерных пленок, волокон); гетерогенный катализ (например, реакция между оксидом углерода и водородом при синтезе метанола, протекающая при контакте с высокодисперсным кизельгуром или силикагелем, на которые нанесена смесь Co–TiO₂–MgO); фракционирование и анализ многокомпонентных систем (адсорбционная хроматография).

«Классические» теории адсорбции были разработаны в начале XX в. Они рассматривают обратимые процессы, исходя из общей трактовки сил межмолекулярного взаимодействия и охватывают процессы физической адсорбции и обратимые хемосорбционные процессы.

В 1915 г И. Ленгмюр и М. Поляни одновременно и независимо друг от друга создали две совершенно разные теории.

Ленгмюр исходил из предположения, что адсорбция является химическим процессом, и адсорбированные молекулы на поверхности адсорбента располагаются в виде одного слоя атомов или молекул. Поляни считал, что адсорбция представляет собой физический процесс и что адсорбционная фаза состоит из многих слоев молекул. Обе теории были во многих отношениях плодотворны и обе имели определенные ограничения. Теория Поляни применима только к ван-дер-ваальсовой адсорбции, теория Ленгмюра, с известными ограничениями, применима как к химической, так и к физической адсорбции.

Известны три вывода уравнения Ленгмюра: кинетический, данный самим Ленгмюром, термодинамический, данный М. Фольмером, и статистический вывод Р. Фаулера. (Выведите уравнение Ленгмюра, приняв, как и он, что число активных центров на поверхности равно единице, а долю активных мест, связанных с адсорбированными молекулами, т. е. ту часть поверхности, которая занята молекулами адсорбата, обозначьте через Θ.)

Для обработки экспериментальных данных обычно используется линейная форма уравнения Ленгмюра:

В этом случае изотерма адсорбции, т. е. зависимость адсорбции от давления адсорбата представляется в виде прямой линии, и появляется возможность определить важнейшие адсорбционные константы (k и p_∞). (Вы помните, какой физический смысл имеют эти величины?)

К сожалению, изотерма адсорбции не дает конкретных сведений о скорости адсорбции. Кинетика адсорбции является самостоятельной областью исследований. Экспериментальные данные свидетельствуют о том, что адсорбция газов и паров протекает чрезвычайно быстро. Например, противогазный уголь извлекает из воздуха, содержащего 7000 частиц хлорпикрина на миллион частиц смеси, 99,99 % этого вещества за 0,03 секунды.

Скорость адсорбции (как и любой другой гетерогенной реакции) пропорциональна числу возможных соударений молекул со свободной поверхностью. Каждая молекула задерживается на поверхности в течение короткого времени, затем в результате флуктуаций энергии молекулы отрываются от активного центра, уступая место новым. Отношение констант адсорбции и десорбции является постоянной величиной.

Опыт показывает, что уравнение изотермы адсорбции Ленгмюра

,

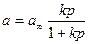
где p – равновесное парциальное давление газа или пара, сравнительно удовлетворительно дает количественную характеристику адсорбции при низких и высоких концентрациях поглощаемого вещества.

Адсорбция газов на твердой поверхности в области средних давлений может быть также описана полуэмпирическим уравнением Бедекера-Фрейндлиха:

где x – количество адсорбированного вещества; m – масса адсорбента; k и 1/n – константы; p – равновесное давление пара или газа в системе.

Несмотря на то, что уравнение Фрейндлиха широко применяется на практике, оно имеет определенные недостатки. Многочисленные исследования показали, что значения величины адсорбции, вычисляемые на основании этого уравнения, не соответствуют данным опыта в области малых и больших концентраций. Константы k и 1/n не имеют определенного физического смысла и являются исключительно эмпирическими.

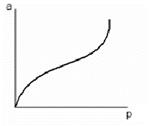
Было установлено, что наряду с изотермами монослойной адсорбции, на практике часто встречаются изотермы, не имеющие второго участка, почти параллельного оси абсцисс и отвечающего насыщению адсорбента адсорбатом:

Для объяснения этого явления М. Поляни предложил теорию полимолекулярной адсорбции, называемую также потенциальной теорией Поляни.

По теории Ленгмюра молекулы адсорбата, притянутые к отдельным активным точкам, между собой не взаимодействуют. Однако при накоплении в адсорбционном слое молекул веществ с большой молекулярной массой, между ними могут возникнуть значительные силы сцепления. В этом случае уравнение Ленгмюра дает неверные результаты. В ряде случаев, в частности при применении пористых адсорбентов, таких, как уголь, силикагель и др., формула Фрейндлиха дает лучшие результаты, чем уравнение Ленгмюра.

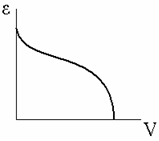
В соответствии с теорией Поляни для каждой пары адсорбент-адсорбат характеристическая кривая, т. е. зависимость адсорбционного потенциала ε от объема V, заключенного между поверхностью, соответствующей данному потенциалу, и поверхностью адсорбента, устанавливается по экспериментально определяемой изотерме адсорбции. Эта зависимость имеет вид:

где V_м – молярный объем газа; p_s – равновесное давление в газовой фазе вне адсорбционного слоя; p – давление насыщенного пара в области поверхностного слоя.

(Дайте определение ε как работы!)

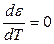
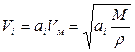
Характеристические кривые инвариантны по температуре: . Указанное свойство характеристической кривой имеет огромное практическое значение, так как позволяет по одной экспериментальной изотерме адсорбции построить через кривую ε–V, семейство изотерм для любых заданных значений по схеме:

( , где ρ – плотность вещества в жидком состоянии)

Для другого адсорбата изотерму можно вычислить по уже найденной характеристической кривой.

Адсорбционный потенциал для данного адсорбента ε₁ изменяется одинаково для всех адсорбируемых веществ. Поэтому при равных заполнениях адсорбционного слоя отношение адсорбционных потенциалов двух адсорбатов является постоянной величиной:

Кривые с постоянным отношением ординат называются аффинными (от лат. affinus – родственный, соответственный). Поэтому β называют коэффициентом аффинности.

В целом, теория Поляни, несмотря на свою ограниченность (отсутствие аналитического выражения для изотермы), отнюдь не потеряла практического значения и до настоящего времени остается теорией, пригодной для описания адсорбции на адсорбентах с резкой энергетической неоднородностью, например, на активированных углях.

Делались попытки обобщить теории Ленгмюра и Поляни. Одной из наиболее удачных попыток является так называемая теория БЭТ (теория Брунауэра-Эммета-Теллера, 1935-1940 гг).

Основные положения теории БЭТ:

1. На поверхности адсорбента имеется определенное число активных центров.
2. Взаимодействием адсорбированных молекул в первом и последующих слоях пренебрегают.
3. Каждая молекула первого слоя может стать активным центром для адсорбции образования последующих слоев.
4. Предполагается, что во втором и последующих слоях все молекулы имеют такую же сумму статистических состояний, как и жидкости.

Уравнение изотермы адсорбции в линейном виде (Запишите его!) позволяет графически определить параметры c и Γ_∞. (Вспомните, c – это концентрация?)

От адсорбции газов и паров существенно отличается адсорбция из растворов на твердой поверхности. Так при адсорбции газов поверхность адсорбента с ростом давления постепенно заполняется адсорбатом в соответствии с изотермой адсорбции. При адсорбции из жидких растворов поверхность адсорбента всегда полностью занята молекулами растворителя и растворенного вещества. Растворенное вещество может адсорбироваться на адсорбенте, только вытесняя молекулы растворителя с его поверхности.

Для характеристики равновесной адсорбции из раствора используют какую-либо изотерму адсорбции.

Для достаточно разбавленных растворов адсорбция хорошо описывается уравнением Ленгмюра или Бедекера-Фрейндлиха, которое для адсорбции из растворов имеет вид:

.

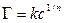
Для экспериментального исследования адсорбции из растворов используют другие уравнения, например:

где Г_экс – количество вещества, адсорбированного 1 г адсорбента, моль/г; c_o и c – начальная и равновесная концентрации адсорбата, моль/дм 3 ; V – объем раствора, из которого происходит адсорбция, дм 3 ; m – масса адсорбента.

Существенную роль при адсорбции из жидких растворов играет природа растворителя и адсорбента. Общее правило: чем лучше данный растворитель смачивает адсорбент, тем меньше адсорбция растворенного вещества и наоборот. Адсорбция растворенного вещества на твердой поверхности будет тем больше, чем больше разность полярностей между растворителем и адсорбентом, и наоборот. Таким образом, адсорбция идет в сторону уравнивания полярностей и тем сильнее, чем больше разность полярностей (правило уравнивания полярностей Ребиндера).

Адсорбция электролитов из водных растворов на твердых адсорбентах является еще более сложным процессом, чем молекулярная адсорбция. На адсорбции ионов существенно сказывается природа адсорбента. Так, ионы, способные поляризоваться, адсорбируются обычно на поверхностях, состоящих из полярных молекул или ионов. Процесс адсорбции ионов усложняется еще и тем, что он, как правило, необратим.

Радиус ионов сильно влияет на их способность адсорбироваться. Так, из ионов одинаковой валентности лучше адсорбируются ионы, имеющие больший радиус, т. к., во-первых, такие ионы сильнее поляризуются, а во-вторых, меньше гидратируются. Среди ионов, имеющих различные заряды, как правило, лучше адсорбируются ионы с бóльшим зарядом. Ряды ионов, составленные в порядке уменьшения их способности связывать воду, называются лиотропными рядами (рядами Гедройца или рядами Гофмейстера).

Несомненный интерес для коллоидной химии представляет адсорбция ионов поверхностью кристалла. В этом случае адсорбцию можно рассматривать как кристаллизацию, т. е. достройку кристаллической решетки способным адсорбироваться ионом (Вспомните правило Панета-Фаянса о способности ионов достраивать кристаллическую решетку, которое Вы изучали, когда рассматривали формирование мицелл в золях!) При этом на кристалле образуется двойной электрический слой (ДЭС).

Если же на поверхности адсорбента уже имеется ДЭС, то при контакте этого адсорбента с электролитом почти всегда в той или иной степени происходит ионообменная адсорбция. Подвижные противоионы электрического слоя способны обмениваться на другие ионы того же знака, находящиеся в растворе.

Первые сообщения об ионообменной адсорбции были сделаны Томпсоном и Уэсли в 1850 г. Они установили, что между водными растворами солей и почвами происходит обмен ионами. Вещества, способные к ионному обмену и используемые для адсорбции ионов, получили название ионообменников или ионитов.

Иониты имеют каркасную структуру, «сшитую» ковалентными связями. Заряд каркаса скомпенсирован противоположным зарядом подвижных противоионов, находящихся в адсорбционной и диффузионной частях ДЭС.

Иониты делятся на органические и неорганические (по составу), на природные и синтетические (по происхождению), на катиониты, аниониты и амфолиты (по заряду обмениваемых ионов; последние способны обменивать как катионы, так и анионы).

Под емкостью ионита понимают его способность обменивать ионы, которая определяется числом функциональных групп и теоретически является величиной постоянной, а практически – зависит от ряда условий.

Статическая обменная емкость (СОЕ) – полная емкость, характеризующая общее число обменных групп (ммоль экв на 1 г воздушно сухого ионита или на 1 см 3 набухшего).

Динамическая обменная емкость (ДОЕ) – определяется той частью ионогенных групп, которая участвует в обмене в технологических условиях, например, в ионообменной колонке при движении раствора относительно ионита. ДОЕ всегда меньше СОЕ, она зависит от скорости движения раствора, размера колонки и др.

Вопросы и задания для самоконтроля знаний по материалу 11-й лекции

1 Сформулируйте основные положения теории Ленгмюра и запишите уравнение изотермы адсорбции.

2 Проанализируйте уравнение при а) c → ∞; б) c → 0; в) Г=Г/2. Чему равна константа k?

3 Как Вы понимаете термины «мономолекулярная адсорбция» и «полимолекулярная адсорбция»?

4 Входит ли в теорию Поляни представления о локализованной адсорбции?

5 Что такое адсорбционный объем, адсорбционный потенциал, характеристическая кривая?

6 Охарактеризуйте практические возможности теории Поляни, исходя из того, что Вы имеете изотерму адсорбции вещества на адсорбенте. Какие зависимости можно получить, пользуясь этой теорией и экспериментальной изотермой адсорбции?

7 Каковы основные положения теории БЭТ и ее практическое значение? Какую важнейшую характеристику адсорбента получают, пользуясь этой теорией?

8 В чем заключаются особенности адсорбции из растворов?

9 Объясните, почему при высоких концентрация растворенного вещества удельная адсорбция 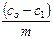часто становится отрицательной величиной, т. е. кривая зависимости удельной адсорбции от концентрации опускается ниже оси абсцисс.

10 Будет ли отличаться ориентация молекул ПАВ при адсорбции из водных растворов на угле и силикагеле?

11 Какое правило установил П. Ребиндер для адсорбции из растворов?

12 К. Гедройц установил, что носителем обменной адсорбции в почве является почвенный поглощающий комплекс, который представляет собой высокодисперсную смесь нерастворимых в воде алюмосиликатных, органических и органоминеральных соединений. В обмене участвуют только катионы. Какой из перечисленных ионов вытесняет больше бария из образца черноземной почвы: Mg 2+ , Li + , K + , Rb + , Cu 2+ ? Расположите эти ионы в порядке увеличения вытеснительной способности.

Знакомимся с основными понятиями физической химии (для курсантов военного факультета)

Повторяем курс физической химии (для студентов химического факультета)

ЛЕКЦИЯ 12

«Джона Мангльса вдруг осенила идея. «Жир! – вскричал он. – Жир, ребята. Тащите сюда баки с тюленьим жиром». Команда сразу поняла мысль капитана. Он хотел применить средство, иногда дающее отличные результаты: можно умерить ярость волн, вылив на них слой жидкого жира; этот слой всплывает на поверхность и ослабляет волны. Жир успокаивает волны мгновенно, но действие его кратковременно»

Вы, наверное, неоднократно могли наблюдать образование тонких пленок различных веществ на поверхности воды или других жидкостей. Приведите примеры таких пленок. Каков механизм их образования?

В качестве примера можно привести образование на поверхности воды пленок нефти, бензина, масел, ПАВ. Такие пленки могут быть невидимы невооруженным глазом (пленки моющих веществ), проявляться в виде интерференционной картины (тонкие слои бензина, нефти) или могут быть обнаружены как достаточно толстые окрашенные пленки (пленки нефти, нафталина).

Пленки на поверхности жидкости могут образовываться двумя способами:

-Адсорбцией веществ из объема раствора на его поверхности (слои Гиббса). По такому механизму образуются пленки малорастворимых в данном растворителе веществ, которые являются по отношению к нему поверхностно-активными (водные растворы моющих средств, малорастворимых спиртов, кислот и др.). Возможен также механизм адсорбции веществ из газовой фазы.

-Непосредственным нанесением вещества на поверхность жидкости получают пленки нерастворимых веществ (слои Ленгмюра). В случае жидкостей (нефть, масла и др.) пленки формируются за счет самопроизвольного растекания. (Сформулируйте условия, при которых реализуется неограниченное растекание жидкости по поверхности другой жидкости с образованием монослоя.) Твердые вещества наносят либо в виде порошка, либо в виде раствора в легколетучем растворителе, который впоследствии может быть удален испарением (нафталин, камфара и др.).

Молекулы вещества, образующие поверхностную пленку на поверхности жидкости, взаимодействуют не только с ее молекулами, но и друг с другом. Интенсивность обоих взаимодействий существенно зависит (помимо температуры) как от природы вещества и жидкости, так и от толщины пленки. Поверхностные пленки по аналогии с резиновыми пленками (Почему такая аналогия не может быть полной?) характеризуются давлением, которое называют поверхностным или двухмерным. Опишите устройство и принцип действия прибора, сконструированного Ленгмюром для измерения двухмерного давления поверхностных пленок.

Прибор Ленгмюра представляет собой плоскую кювету с гидрофобизированными парафином стенками. На поверхности кюветы помещают легкий плавающий барьер, соединенный с динамометром. В современных вариантах прибора используют высокочувствительные автоматические силоизмерители. В кювету наливают до краев воду и в промежуток между подвижным (измерительным) и неподвижным (вспомогательным) барьерами наносят измеряемое вещество (ПАВ), образующее поверхностную пленку. Двухмерное давление π, создаваемое пленкой, действует на измерительный барьер. Оно пропорционально показаниям динамометра:

,

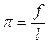
где f – сила, фиксируемая динамометром; l – ширина барьера.

Для изменения площади поверхности, на которой нанесено заданное количество вещества (т. е. для изменения степени заполнения поверхности, которое влияет на состояние пленки), передвигают неподвижный вспомогательный барьер. (Каково типичное значение двухмерного давления нерастворимых пленок?)

Проанализируйте зависимость π–s_м, получаемую в результате проведения описанного эксперимента. Какую информацию об исследуемом веществе можно получить из данной зависимости?

По зависимости поверхностного давления пленки от значения адсорбции Γ (или площади поверхности, приходящейся на 1 молекулу (или 1 моль) вещества пленки s_м (S_м), можно судить об агрегатном состоянии пленки. Эта зависимость аналогична изотерме для реальных газов и паров. Так, при больших значениях s_м (пленка сильно растянута) молекулы пленки расположены на большом расстоянии друг от друга и ведут себя подобно двухмерному газу, поэтому зависимость π–s_м представляет собой линейный участок, параллельный оси абсцисс. В результате выполнения многочисленных исследований Ленгмюра и его последователей (Н. Адама, Е. Райдила и др.) было показано, что для широкого круга веществ независимо от природы молекул ПАВ при Γ → 0 справедливо выражение π∙s_м → k_Б∙T.

По мере увеличения s_м (за счет приближения вспомогательного барьера к измерительному и/или увеличения концентрации ПАВ) молекулы ПАВ приближаются друг к другу. При достижении некоторого предела молекулы образуют сплошную жидкую пленку в виде монослоя, что соответствует резкому увеличению π вследствие малой сжимаемости жидкости. Если притяжение молекул выражено слабо, то зависимость двухмерного давления от площади поверхности, приходящуюся на одну молекулу, может быть описана предложенным Фольмером выражением, аналогичным уравнению идеального газа с введенной поправкой на собственный объем молекулы:

.

Однако рост двухмерного давления при сжатии адсорбционного слоя ограничен некоторой величиной π_max, которая называется давлением коллапса, так как при этом мономолекулярный слой, как правило, теряет свою устойчивость, на его поверхности образуются складки и возникают полимолекулярные участки.

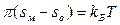
По изотермам поверхностного давления можно не только установить тип поверхностной пленки, но и определить размеры и форму молекул ПАВ, образующих пленку.

Значение s_o, соответствующее π_max, можно принять за площадь, занимаемую одной молекулой ПАВ при предельном заполнении монослоя, т. е. она равна площади поперечного сечения одной молекулы ПАВ:

.

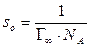
Величина s_o приблизительно постоянна для неразветвленных членов гомологического ряда некоторых классов ПАВ (вспомните правило Дюкло-Траубе!). Более того, s_o не зависит от природы полярной группы, что свидетельствует о том, что она определяется площадью поперечного сечения углеводородной цепи.

Часто изотерму поверхностного давления строят в координатах πs_м – π:

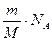
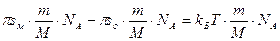
Если неизвестна молекулярная масса ПАВ, то надо преобразовать полученное выражение, умножив его каждый член на . В результате получим:

,

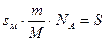
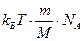
где – макроплощадь, занятая пленкой.

Далее обозначим как в и построим график в координатах πS – π:

Так находят молекулярную массу белков.

(Каким образом изменяются свойства жидкости при образовании на ее поверхности пленки ПАВ?)

Видео:Галилео. Эксперимент. Поверхностное натяжениеСкачать

1.5. Поверхностное натяжение растворов и адсорбция

Свободная поверхностная энергия самопроизвольно может только уменьшаться, что проявляется в уменьшении либо поверхности раздела фаз, либо межфазного (поверхностного) натяжения. Поверхностное натяжение может уменьшаться в результате самопроизвольного перераспределения компонентов системы между объемами фаз a и b и поверхностью их раздела. В поверхности раздела фаз будут преимущественно концентрироваться те компоненты, которые способны уменьшать избыточную свободную поверхностную энергию. Это явление получило название «адсорбция». Количественно мерой адсорбции служит избыток вещества в поверхностном слое определенной толщины по сравнению с его количеством в таком же слое в объеме фазы. Этот избыток обычно относят к единице площади поверхности (или к единице массы адсорбента). Такая адсорбция называется гиббсовской и обозначается буквой Г_i. Поверхностный избыток является алгебраической величиной. Если он положителен, то вблизи поверхности данный компонент присутствует в избытке, если отрицателен, то концентрация компонента на поверхности фазы ниже, чем в ее объеме .

Рассмотрим распределение в системе i -го компонента, предполагая, что это вещество способно понижать поверхностное натяжение. В соответствии с уравнением (1.1.6) число молей n вещества i-го компонента в системе определяется как .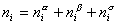

Количество вещества в обеих фазах составляет

. (1.1.81)

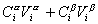
где С a , С b — концентрация вещества в фазах a, b.

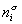
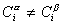
Количество вещества на поверхности раздела фаз , избыточное по отношению к объемам фаз V a и V b , оказывается зависимым от положения разделяющей плоскости, так как концентрации вещества в различных фазах не равны, .

Учитывая уравнение (1.1.81) ,

. (1.1.82)

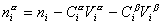
Разделив выражение (1.1.82) на площадь поверхности раздела фаз А, можем определить гиббсовскую адсорбцию:

. (1.1.83)

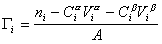
Фундаментальным уравнением физической химии поверхностей является взаимосвязь между адсорбцией и межфазным натяжением, которую можно определить экспериментально при одновременном изменении многих факторов. Остановимся на системах, в которых адсорбция протекает при постоянной температуре. Связь между адсорбцией и межфазным натяжением при постоянной температуре T называется изотермой адсорбции, фундаментальное уравнение которой известно как уравнение Гиббса. Рассмотрим его вывод.

При небольшом обратимом изменении энергии системы dU с учетом формулы (1.1.4) можем написать

, (1.1.84)

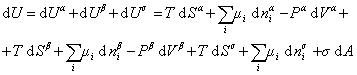
где U – полная внутренняя энергия системы; U a , U b , U s – внутренняя энергия фаз aиb и поверхности их раздела; P a , P b — давление в фазах aиb; m — химический потенциалi-того компонента; S a , S b , S s – энтропия фаз a иb и их поверхности раздела; s — поверхностное натяжение.

Поскольку из курса химической термодинамики известно, что

(1.1.85)

, (1.1.86)

. (1.1.87)

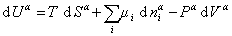
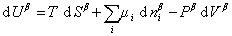
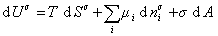
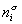
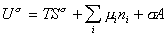
Если энергию, энтропию и количество компонентов увеличивать от нуля до некоторого определенного значения при постоянстве температуры T, площади поверхности раздела фаз A и количестве вещества на этой поверхности , то уравнение (1.1.87) переходит в общее уравнение

, (1.1.88)

дифференцирование которого приводит к выражению

. (1.1.89)

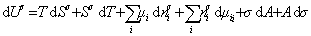
Сравнивая его с уравнением (1.1.88), получаем

. (1.1.90)

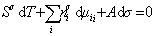
В расчете на единицу поверхности

, (1.1.91)

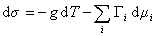
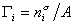
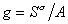
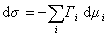
где – гиббсовская адсорбция; – удельная энтропия поверхностного слоя.

. (1.1.92)

Для двухкомпонентной системы

, (1.1.93)

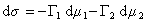
где индекс 1 относится к растворителю, а индекс 2 – к растворенному веществу.

Рис. 1.15. Схема реальной (I) межфазовой области и идеальной (II) и (III) разделяющей межфазовой поверхности (поверхности Гиббса)

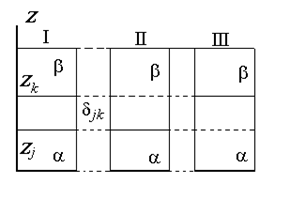
Разделяющая поверхность Гиббса может быть проведена так, чтобы обратилась в нуль адсорбция любого наперед заданного компонента, но только одного, как это показано на рис. 1.15.

Расстояние между двумя плоскостями (разделяющими поверхностями), одна из которых соответствует условию Г_j = 0, а другая — Г_k = 0, обозначим d_kj:

, (1.1.94)

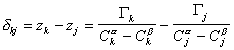
где Г_k, Г_j– избытки рассматриваемых компонентов в поверхностном слое ; C_k a , C_k b , C_j a , C_j b – концентрация компонентов k и j в фазах a и b; z_k, z_j – координаты разделяющей поверхности.

Поскольку значения Г₁ в уравнении (1.1.93) определены относительно произвольно выбранного положения разделяющей плоскости, то ее можно расположить так, чтобы избыток растворителя в поверхностном слое был равен нулю ( Г₁ = 0).

, (1.1.95)

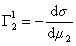
где верхний индекс 1 означает, что для выбранной поверхности раздела Г₁=0.

, (1.1.96)

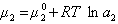
получаем после дифференцирования уравнения (1.1.96)

, (1.1.97)

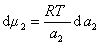
где 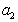— активность растворенного вещества.

Поэтому, подставляя уравнение (1.1.97) в уравнение (1.1.95), получаем

. (1.1.98)

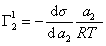
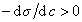
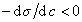
Из уравнения (1.1.98) следует, что если , то адсорбция положительна, а при возникает дефицит растворенного вещества на разделяющей поверхности .

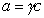
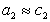
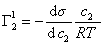
Поскольку , где g – коэффициент активности, который для разбавленных растворов стремится к единице, то и

. (1.1.99)

Уравнение (1.1.99) представляет собой наиболее употребляемую форму изотермы адсорбции Гиббса, причем так как рассматривается адсорбция именно растворенного вещества, индексы при адсорбции и концентрации опускают, т.е.

. (1.1.100)

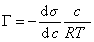
Исследования показывают, что существуют такие вещества, растворение которых приводит к резкому снижению поверхностного натяжения раствора. Эти вещества называют поверхностно-активными. В соответствии с уравнением Гиббса адсорбция их всегда положительна, т.е. концентрация в поверхностном слое выше объемной концентрации. По предложению Ребиндера мера поверхностной активности обозначается первой буквой фамилии Гиббса. Обычно используют значения поверхностной активности в бесконечно разбавленных растворах

. (1.1.101)

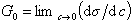
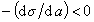
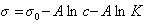
К классу поверхностно-активных веществ (ПАВ) относятся жирные кислоты и их соли (мыла), сульфокислоты, их соли, спирты, алкилсульфоэфиры и др. Если , то Г >1, то единицей в уравнении Шишковского (1.1.105 ) можно пренебречь, тогда

. (1.1.106)

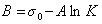
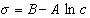
Обозначим постоянной В постоянные при изотермических условиях величины , тогда

. (1.1.107)

Следовательно, при относительно высокой концентрации растворов ПАВ их поверхностное натяжение должно уменьшаться экспоненциально с увеличением концентрации.

Уравнение (1.1.107) может быть получено непосредственно из уравнения изотермы адсорбции Гиббса:

.

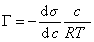
При достаточно высокой концентрации растворенного вещества адсорбция достигает предела , т.е. Г = Г_max , поэтому

, (1.1.108)

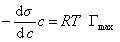
где при постоянной температуре правая часть представляет собой постоянную величину и может быть обозначена RT Г_max = A. Следовательно,

,

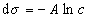
откуда после интегрирования получаем

. (1.1.109)

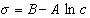
Таким образом, уравнение Шишковского может быть выведено из уравнения Гиббса, так как уравнения (1.1.107) и (1.1.109) идентичны. Точность уравнения Шишковского связана с тем, что в нем уже заложено условие насыщения адсорбционного слоя.

Если уравнение Шишковского в форме

(1.1.110)

, (1.1.111)

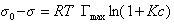
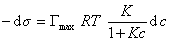
и подставить в уравнение Гиббса величину

, (1.1.112)

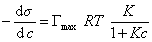
то уравнение изотермы адсорбции примет вид

. (1.1.113)

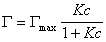
В такой форме уравнение изотермы адсорбции носит название изотермы Ленгмюра. Американский ученый И. Ленгмюр в 1917 г. развил представление о мономолекулярной адсорбции и на основании молекулярно- кинетической теории получил уравнение (1.1.113) .

Уравнение Шишковского позволяет определить предел адсорбции (при Kc>>1), так как в таком случае это уравнение принимает вид

. (1.1.114)

Рис. 1.16. Зависимость поверхностного натяжения от концентрации растворов ПАВ в координатах уравнения Шишковского

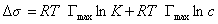
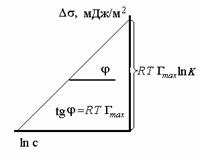
Построив график 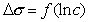, как это показано на рис. 1.16, по углу наклона можно определить предел адсорбции, а по отрезку, отсекаемому наклонной линией на оси ординат при ln c = 0, рассчитать постоянную равновесия процесса адсорбции K.

Понимание адсорбционных процессов имеет чрезвычайно важное значение, так как они лежат в основе многих процессов, протекающих на границе раздела фаз, например крашения, отмывания загрязнений, отделки текстильных материалов и т.д., т.е. в основе всех коллоидно -химических процессов на границе жидкость–газ.

🌟 Видео

Поверхностное натяжение и адгезия (видео 17) | Жидкости | ФизикаСкачать

Поверхностное натяжение (видео 3) | Силы межмолекулярного взаимодействия | ХимияСкачать

4.1. Поверхностное натяжениеСкачать

Поверхностные явления. Адсорбция.Скачать

Адсорбция на поверхностях растворовСкачать

5.1. Адсорбция. Классификация адсорбцииСкачать

Поверхностные явления: адгезия, смачивание, адсорбция | Коллоидная химияСкачать

Насыщенный и ненасыщенный пар. Влажность воздуха. 10 класс.Скачать

Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать

4.2. Межмолекулярные и межфазные взаимодействияСкачать

Поверхностное натяжениеСкачать

АдсорбцияСкачать

Свойства поверхностного слоя жидкости. 10 класс.Скачать

5.2. Молекулярная адсорбция ПАВ на поверхности раздела раствор-воздухСкачать

Урок 198. Простейшие задачи на поверхностное натяжениеСкачать

Физика. 10 класс. Поверхностное натяжениеСкачать