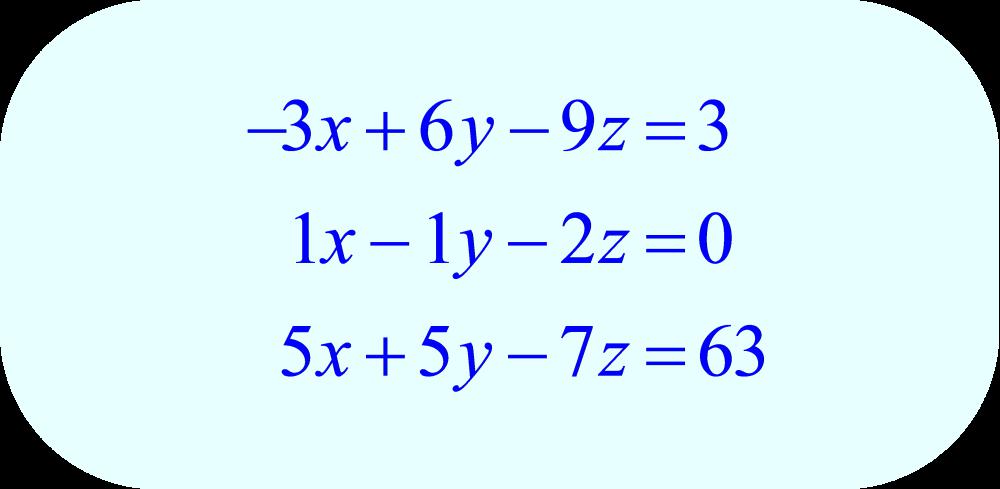Какие уравнения не имеют решений 2 класс (6 видео)

ГДЗ учебник по математике 2 класс Петерсон. Урок 33. Связь умножения и деления. Номер №8

Какие уравнения не имеют решений, а в каких решением является любое число?
x * 1 = x
0 * x = 2
x : 1 = x
x : 0 = 0

Содержание

Решение
Пушкин сделал!
Урок 33. Связь умножения и деления. Л.Г. Петерсон Математика 2 класс Ответы
4. Объясни по рисунку смысл равенств, где а и b — длина и ширина прямоугольника, а S — его площадь.
8. Какие уравнения не имеют решений, а в каких решением является любое число?
10. Составь слова и исключи лишнее слово:
УДБ НЁКЛ АНИБЯР ФАШК АИСОН
Какое уравнение не имеет корней? Примеры уравнений
Какое уравнение не имеет корней?
1. Линейное уравнение
2. Квадратное уравнение
3. Тригонометрические уравнения
4. Системы уравнений
Обобщение и советы по нахождению корней уравнения
🎬 Видео

Решение

Не имеют решений:
0 * x = 2 − при умножении любого числа на 0, произведение всегда будет равно 0 ;
x : 0 = 0 − на 0 делить нельзя.

Решением является любое число:
x * 1 = x − при умножении любого числа на 1, произведение всегда будет равно этому числу;
x : 1 = x − при делении любого числа на 1, частное всегда будет равно этому числу.

Видео:Математика 2 класс (Урок№26 - Уравнение. Решение уравнений подбором неизвестного числа.)Скачать

Пушкин сделал!

Разбор домашних заданий 1-4 класс

Home » Петерсон Математика » Урок 33. Связь умножения и деления. Л.Г. Петерсон Математика 2 класс Ответы

Видео:РЕШЕНИЕ УРАВНЕНИЙ |ПОДРОБНОЕ ОБЪЯСНЕНИЕ КАК РЕШИТЬ УРАВНЕНИЯ / ПРОСТЫЕ УРАВНЕНИЯ 2 КЛАСС МАТЕМАТИКАСкачать

Урок 33. Связь умножения и деления. Л.Г. Петерсон Математика 2 класс Ответы

Объясни по рисункам смысл равенств. Что ты замечаешь?

Решение

Если взять по два три раза или по три два раза, то получим одно и то же произведение 6. Если произведение разделим на один из множителей, то получим другой множитель.

2. Объясни по рисунку смысл равенств.

Что означают первые два равенства? Третье и четвертое равенства? Что тебе напоминают эти 4 равенства?

Решение

Первые два равенства означают, если нужно вычислить произведение чисел 3 и 4, то от перемены их местами все равно получится 12. Если произведение 12 разделить на один из множителей 3 или 4, то получим другой множитель 4 или 3. Эти равенства напоминают таблицу умножения и деления.

3. Пользуясь таблицей умножения, составь 4 равенства из чисел:

а) 3, 6 и 18; б) 8, 3 и 24; в) 3, 7 и 21.

Решение

Видео:Система уравнений не имеет решений или имеет бесчисленное множество решенийСкачать

4. Объясни по рисунку смысл равенств, где а и b — длина и ширина прямоугольника, а S — его площадь.

Что ты замечаешь? Сделай вывод.

Решение

Первые два равенства показывают, как найти площадь прямоугольника, которая равна произведению его сторон а и b или b и а. Если площадь разделить на одну из сторон прямоугольника, то получится его другая сторона.

Зная площадь прямоугольника и длину одной из сторон, можно найти длину другой стороны.

5. Найди длину неизвестной стороны прямоугольника:

Решение

а) Чтобы найти неизвестную сторону прямоугольника, надо площадь разделить на известную сторону.

б) Чтобы найти неизвестную сторону прямоугольника, надо площадь разделить на известную сторону.

в) Чтобы найти неизвестную сторону прямоугольника, надо площадь разделить на известную сторону.

6. Площадь прямоугольника 14 см², а длина — 7 см. Найди ширину и периметр прямоугольника.

Решение

1) 14 : 7 = 2 (см) – ширина прямоугольника.

2) (7 + 2) ∙ 2 = 18 (см) — периметр прямоугольника.

Ответ: 2 см, 18 см.

7. а) Длина прямоугольника 6 см. Это на 4 см больше, чем ширина. Построй этот прямоугольник, найди его периметр и площадь.

б) Составь все возможные равенства из чисел, выражающих длины сторон и площадь построенного прямоугольника.

Решение

а) 1) 6 – 4 = 2 (см) – ширина прямоугольника.

2) (6 + 2) ∙ 2 = 16 (см) — периметр прямоугольника.

3) 6 ∙ 2 = 12 (см²) – площадь прямоугольника.

Видео:Решение уравнений сложной структуры 2 классСкачать

8. Какие уравнения не имеют решений, а в каких решением является любое число?

х ∙ 1 = х 0 ∙ х = 2 х : 1 = х х : 0 = 0

Решение

х ∙ 1 = х Решением уравнения является любое число, так как при умножении любого числа на 1 получается то же самое число.

0 ∙ х = 2 У этого уравнения нет решений, так как при умножении нуля на любое число получается нуль

х : 1 = х Решением уравнения является любое число, так как при делении любого числа на 1 получается то же самое число. х : 0 = 0 У этого уравнения нет решений, так как нуль делить нельзя.

9. Составь программу действий и вычисли:

Решение

Видео:Уравнение | Математика 2 класс #19 | ИнфоурокСкачать

10. Составь слова и исключи лишнее слово:

Видео:Математика 2 класс. «Сложные уравнения и их решение»Скачать

УДБ НЁКЛ АНИБЯР ФАШК АИСОН

Решение

ДУБ КЛЁН РЯБИНА ШКАФ ОСИНА

Лишнее слово – ШКАФ, так как это мебель, а все остальные слова – названия деревьев.

Здравствуйте! Меня зовут Мария, я автор сайта Пушкин сделал. Надеюсь, что мой сайт вам помогает, в свою очередь прошу помощи у вас. Моему сыну поставили диагноз аутизм. Ему необходимы ежедневные коррекционные занятия, если вы можете помочь, буду вам благодарна. Каждые ваши 10 рублей — еще один шанс для моего ребенка жить полноценной жизнью. Страница для сбора здесь

Видео:6. ПРИ КАКИХ ЗНАЧЕНИЯХ ПАРАМЕТРА УРАВНЕНИЕ НЕ ИМЕЕТ КОРНЕЙСкачать

Какое уравнение не имеет корней? Примеры уравнений

Решение уравнений в математике занимает особое место. Этому процессу предшествует множество часов изучения теории, в ходе которых ученик узнает способы решения уравнений, определения их вида и доводит навык до полного автоматизма. Однако далеко не всегда поиск корней имеет смысл, так как их может попросту не быть. Существуют особые приемы нахождения корней. В данной статье мы разберем основные функции, их области определения, а также случаи, когда их корни отсутствуют.

Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Какое уравнение не имеет корней?

Уравнение не имеет корней в том случае, если не существует таких действительных аргументов х, при которых уравнение тождественно верно. Для неспециалиста данная формулировка, как и большинство математических теорем и формул, выглядит очень размытой и абстрактной, однако это в теории. На практике все становится предельно просто. Например: уравнение 0 * х = -53 не имеет решения, так как не найдется такого числа х, произведение которого с нулем дало бы что-то, кроме нуля.

Сейчас мы рассмотрим самые базовые типы уравнений.

Видео:Математика. Уравнения. Решение уравнений. 2 класс.Скачать

1. Линейное уравнение

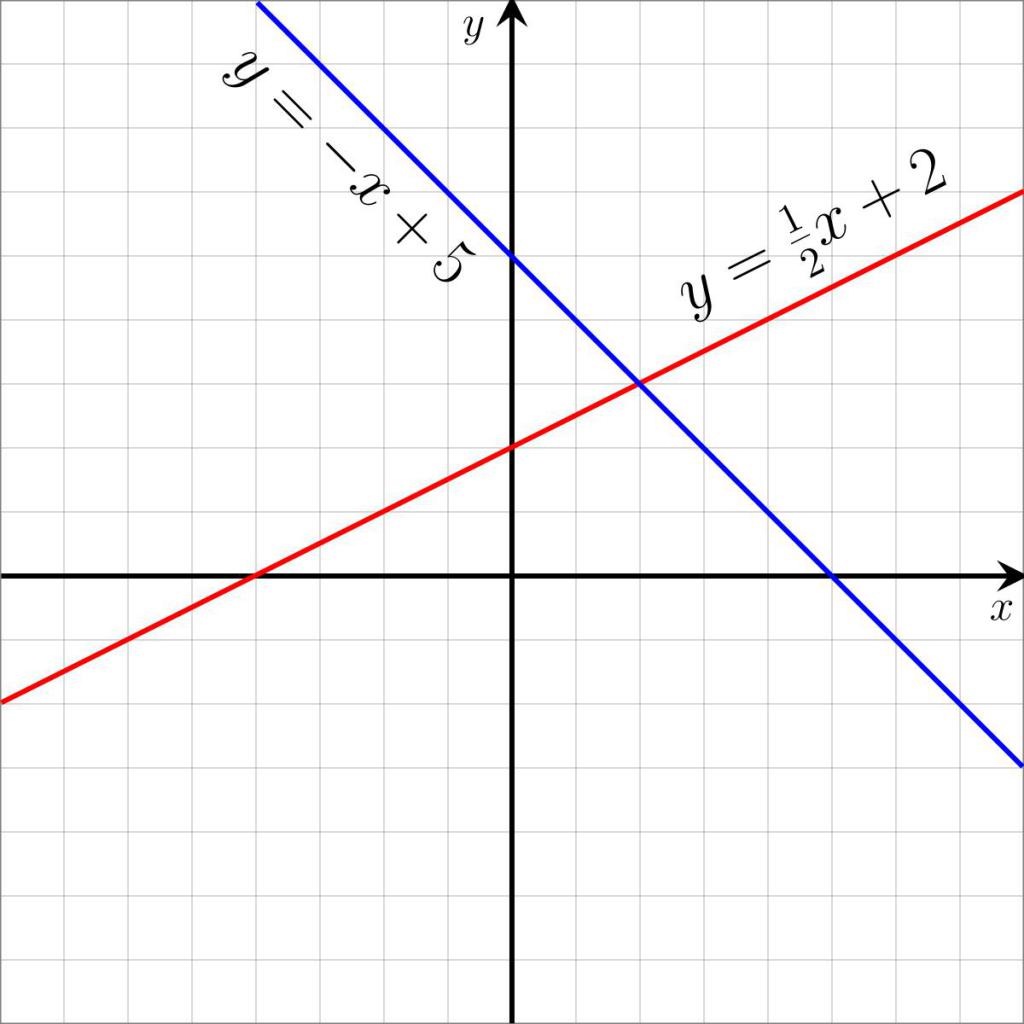
Уравнение называется линейным, если его правая и левая части представлены в виде линейных функций: ax + b = cx + d или в обобщенном виде kx + b = 0. Где а, b, с, d — известные числа, а х — неизвестная величина. Какое уравнение не имеет корней? Примеры линейных уравнений представлены на иллюстрации ниже.

В основном линейные уравнения решаются простым переносом числовой части в одну часть, а содержимого с х — в другую. Получается уравнение вида mx = n, где m и n — числа, а х — неизвестное. Чтобы найти х, достаточно разделить обе части на m. Тогда х = n/m. В основном линейные уравнения имеют только один корень, однако бывают случаи, когда корней либо бесконечно много, либо нет вовсе. При m = 0 и n = 0 уравнение принимает вид 0 * х = 0. Решением такого уравнения будет абсолютно любое число.

Однако какое уравнение не имеет корней?

При m = 0 и n = 0 уравнение не имеет корней из множества действительных чисел. 0 * х = -1; 0 * х = 200 — эти уравнения не имеют корней.

Видео:МАТЕМАТИКА 2 КЛАСС: ВИДЕО УРОК 22 - РЕШЕНИЕ УРАВНЕНИЙ | ДИСТАНЦИОННОЕ ОБРАЗОВАНИЕСкачать

2. Квадратное уравнение

Квадратным уравнением называется уравнение вида ax 2 + bx + c = 0 при а = 0. Самым распространенным способом решения квадратного уравнения является решение через дискриминант. Формула нахождения дискриминанта квадратного уравнения: D = b 2 — 4 * a * c. Далее находится два корня х_1,2= (-b ± √D) / 2 * a.

При D > 0 уравнение имеет два корня, при D = 0 — корень один. Но какое квадратное уравнение не имеет корней? Пронаблюдать количество корней квадратного уравнения проще всего по графику функции, представляющем собой параболу. При а > 0 ветви направлены вверх, при а 2 – 8x + 72 = 0 не имеет корней, так как имеет отрицательный дискриминант D = (–8) 2 – 4 * 1 * 72 = -224. Это значит, что парабола не касается оси абсцисс и функция никогда не принимает значение 0, следовательно, уравнение не имеет действительных корней.

Видео:Уравнение 2 класс Школа РоссииСкачать

3. Тригонометрические уравнения

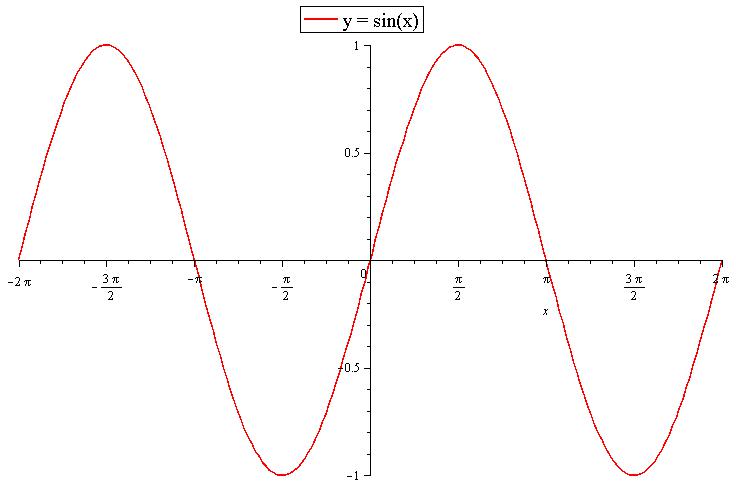
Тригонометрические функции рассматриваются на тригонометрической окружности, однако могут быть представлены и в декартовой системе координат. В данной статье мы рассмотрим две основные тригонометрические функции и их уравнения: sinx и cosx. Так как данные функции образуют тригонометрическую окружность с радиусом 1, |sinx| и |cosx| не могут быть больше 1. Итак, какое уравнение sinx не имеет корней? Рассмотрим график функции sinx, представленный на картинке ниже.

Мы видим, что функция является симметричной и имеет период повторения 2pi. Исходя их этого, можно говорить, что максимальным значением этой функции может быть 1, а минимальным -1. Например, выражение cosx = 5 не будет иметь корней, так как по модулю оно больше единицы.

Это самый простой пример тригонометрических уравнений. На самом деле их решение может занимать множество страниц, в конце которых вы осознаете, что использовали неправильную формулу и все нужно начинать сначала. Порой даже при правильном нахождении корней вы можете забыть учесть ограничения по ОДЗ, из-за чего в ответе появляется лишний корень или интервал, и весь ответ обращается в ошибочный. Поэтому строго следите за всеми ограничениями, ведь не все корни вписываются в рамки задачи.

Видео:Уравнения для 2 класса Математика Как объяснить ребенку решение уравнений 2 классСкачать

4. Системы уравнений

Система уравнений представляет собой совокупность уравнений, объединенных фигурной или квадратной скобками. Фигурные скобки обозначают совместное выполнение всех уравнений. То есть если хотя бы одно из уравнений не имеет корней или противоречит другому, вся система не имеет решения. Квадратные скобки обозначают слово «или». Это значит, что если хотя бы одно из уравнений системы имеет решение, то вся система имеет решение.

Ответом системы с квадратными скобками является совокупность всех корней отдельных уравнений. А системы с фигурным скобками имеют только общие корни. Системы уравнений могут включать абсолютно разнообразные функции, поэтому такая сложность не позволяет сказать сразу, какое уравнение не имеет корней.

Видео:Вариант 40, № 2. Линейное уравнение, не имеющее корнейСкачать

Обобщение и советы по нахождению корней уравнения

В задачниках и учебниках встречаются разные типы уравнений: такие, которые имею корни, и не имеющие их. В первую очередь, если у вас не получается найти корни, не думайте, что их нет совсем. Возможно, вы совершили где-нибудь ошибку, тогда достаточно лишь внимательно перепроверить ваше решение.

Мы рассмотрели самые базовые уравнения и их виды. Теперь вы можете сказать, какое уравнение не имеет корней. В большинстве случаев сделать это совсем не трудно. Для достижения успеха в решении уравнений требуется лишь внимание и сосредоточенность. Практикуйтесь больше, это поможет вам ориентироваться в материале гораздо лучше и быстрее.

Итак, уравнение не имеет корней, если:

в линейном уравнении mx = n значение m = 0 и n = 0;
в квадратном уравнении, если дискриминант меньше нуля;
в тригонометрическом уравнении вида cosx = m / sinx = n, если |m| > 0, |n| > 0;
в системе уравнений с фигурными скобками, если хотя бы одно уравнение не имеет корней, и с квадратными скобками, если все уравнения не имеют корней.