Какие уравнения лежат в основе динамических методов определения момента инерции

Видео:Урок 94. Вычисление моментов инерции телСкачать

К о н т р о л ь н ы е в о п р о с ы

Работа №5. Определение момента инерции тела, скатывающегося

С наклонной поверхности

ЦЕЛЬ: определить момент инерции тела относительно мгновенной оси вращения расчётным и экспериментальным методом

ОБОРУДОВАНИЕ: установка, набор тел, секундомер

В работе используются тела, осью которых является цилиндрический стержень радиусомr. Одно из тел 1 (рис. 1) помещают на параллельные направляющие 2, образующие с горизонтом углы a₁ и a₂.

Если тело отпустить, то оно, скатываясь, достигнет нижней точки и, двигаясь далее по инерции, поднимется вверх по направляющим. Движение тела, при котором траектории всех точек лежат в параллельных плоскостях, называется плоским. Плоское движение можно представить двумя способами: либо как совокупность поступательного движения тела со скоростью центра масс и вращательного вокруг оси, проходящей через центр масс; либо как только вращательное движение вокруг мгновенной оси вращения (МОВ), положение которой непрерывно изменяется. В нашем случае эта мгновенная ось Z проходит через точки касания направляющих с движущимся стержнем.

ОПИСАНИЕ МЕТОДА ИЗМЕРЕНИЙ

При скатывании тело, опускаясь с высоты , проходит путь l_о, а поднимаясь по инерции на высоту , проходит путь l. В нижней точке скорость поступательного движения центра масс , а угловая скорость тела

, (10)

где t – время движения от верхней точки до нижней, r – радиус стержня (оси).

На скатывающееся тело действует момент сил сопротивления М_тр. Работа его на пути l_о равна А=М_трj, где угловой путь j₀=l₀/r.

Закон сохранения энергии на отрезке пути l_о имеет вид

, (11)

где I – момент инерции скатывающегося тела относительно МОВ,

m – масса тела, включающая в себя массу стержня.

При движении тела вниз с высоты h_о и вкатывании его на высоту h работа сил сопротивления на пути (l+l_о) равна убыли потенциальной энергии (см. (2)):

. (12)

Решая совместно (10)–(12), получаем формулу для определения момента инерции динамическим методом:

. (13)

Здесь величина (a₁+ a₂) является константой для данной установки.

Момент инерции тела относительноМОВ определяется теоремой Штейнера

,

где I_O – момент инерции, относительно центра масс;

a – расстояние от центра масс тела до оси вращения(в этом опытеa=r).

Задание 1. Аналитический расчёт момента инерции тела

Для расчёта момента инерции маховика I необходимо измерить массу тела (написана на телах) или объём (массу рассчитать, используя плотность) и радиусы цилиндрических тел. Методика расчёта величины I дана в приложении 1. В соответствии с ней результаты всех измерений и вычислений вносите в табл. 1.

Таблица 1

Индекс	Элементтелавращения	Масса m, кг	Диаметр d, мм, иа, мм	Момент инерции I,кг×м 2
формула	значение
Диск

Далее задание выполняется, как описано в Приложении 1.

Задание 2. Определение момента инерции тела динамическимметодом

1. Определите массу т тела, запишите ее значение, а также постоянную установки (a₁+a₂) в табл. 2.

2. Проверьте правильность положения установки.При скатывании тело не должно смещаться к одной из направляющих. Для регулировки используйте винты основания. Измерьте штангенциркулем диаметр dстержня в различных местах, определите егоcреднее значение и средний радиус r.

3. Установите тело на направляющие на расстоянии l_o от нижней точки, за его положение фиксируется магнитом по нажатию кнопки «Сброс» секундомера.

4. Нажмите кнопку секундомера « Пуск». При этом электромагнит отключится и тело начинает двигаться. Когда тело достигнет нижней точки, секундомер автоматически выключится. Запишите время движения тела до нижней точки в табл. 2.

5. Наблюдая далее за движением тела по инерции, отметьте расстояние l, на которое оно поднимется до остановки.

6. Опыт повторите еще четыре раза при том же расстоянии l_о, записывая результаты в табл. 2.

Таблица 2

№п.п.	d, мм	t, с	l, м	a1+a2= рад m = кг lо = м м
…
Среднее значение	I = кг×м 2

7. Найдите средние значения величин r, t, l и по формуле (3.13) рассчитайте момент инерции тела I относительно МОВ.

Задание3.Изучение зависимости момента инерции от распределения массы относительно оси вращения

В этом задании используется тело в виде крестовины, по которой могут перемещаться грузы (цилиндры). Все результаты измерений заносятся в табл. 3.

1. Определите массу т тела и радиус r оси тела, и запишите постоянную установки (a₁ + a₂).

2. Установите подвижные цилиндры на равном расстоянии bот оси вращения и измерьте это расстояние.

Примечания. 1. Когда грузы находятся на одинаковом расстоянии от оси вращения, тело должно находиться в безразличном положении равновесия на горизонтальных направляющих. 2. Так как цилиндры имеют одинаковый размер, расстояние между центрами грузов равно расстоянию между их торцами,которое можно измерить значительно точнее(рис. 2).

3. Установите тело на направляющие на расстоянии l_o от нижней точки, его положение фиксируется магнитом нажатием кнопки «Сброс» секундомера.

4. Нажмите кнопку секундомера «Пуск». При этом электромагнит отключится и тело начинает двигаться. Когда тело достигнет нижней точки, секундомер автоматически выключится. Запишите время движения тела до нижней точки в табл. 3.

5. Отметьте расстояние l, на которое продвинется тело, поднимаясь по инерции.

6. Повторите измерения пп. 3-5 при других расстояниях b цилиндров, относительно оси вращения.

7. Рассчитайте b 2 и момент инерции тела I (формула 3-13) для каждого опыта.

8. Постройте график зависимости (см. рекомендации построения и обработки графиков) и по графику определите момент инерции крестовиныI_КРи массуmподвижных грузов.

9. Сделайте выводы.

Задание 4.Оценка погрешности измерений

В качестве систематической погрешности в данных опытах следует взять

приборную погрешность, равную цене деления измерительного прибора.

Случайная погрешность определяется по разбросу выборки:

,

где х_max и х_min– максимальное и минимальное значение измеряемой величины в серии из N повторных измерений. Этой границе доверительного интервала соответствует доверительная вероятность

.

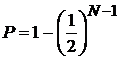
1. В табл. 4 занесите средние значения прямых измерений, выполненных в одном из упражнений и значения погрешностей этих величин – систематической и случайной.

2. Для каждой величины выберете наибольшую из погрешностей и рассчитайте наибольшую относительную погрешность δ измерения каждой величины. В окончательном выводе следует отметить для каких величин желательно увеличить (и как?) точность измерений, а для каких её можно и уменьшить без ущерба для конечного результата.

Таблица 4

ВЕЛИЧИНА	ПОГРЕШНОСТЬ
абсолютная	наибольшая
название	значение	систематич.	случайная	абсолютная	относит.
	рад	––
т	кг	––
	м	––
l	м
r	м
t	с

3. В качестве относительной погрешности результатов измерений примите наибольшую из погрешностей прямых измерений (см. табл. 2)

К о н т р о л ь н ы е в о п р о с ы

1. Укажите величины кинетической и потенциальной энергии при скатывании тела: в начале и в конце движения, в нижней точке и в произвольной точке.

2. Опишите характер движения тела по направляющим. Какая сила создаёт момент относительно оси вращения?

3. Как измеряют угловую скорость w в данной работе?

4. Какие величины измеряют для определения скорости w, момента сил трения, работы сил трения?

5. Какие уравнения лежат в основе динамических методов определения момента инерции?

6. Что составляет основу методики расчётного метода определения величины I?

7. Укажите возможные источники случайных и систематических погрешностей при измерениях.

МЕТОДИКА РАСЧЕТА МОМЕНТА ИНЕРЦИИ ТЕЛ СЛОЖНОЙ ФОРМЫ

ЦЕЛЬ: приобрести навык расчёта момента инерции тел, состоящих из простых элементов.

1. Исследуйте форму тела. Приняв во внимание, что момент инерции любого тела равен сумме моментов инерции отдельных его элементов, мысленно разделите исследуемое тело на простые элементы, для которых формулы расчёта величины I_i даны в табл. 1.

2. Сделайте эскиз исследуемого тела, а если необходимо, то и его элементов, обозначая символами все размеры, подлежащие измерению. Например, тело (рис. 1а) состоит из насаженных на вал 1 шкива 2 и маховика 3 с двумя отверстиями 4. Это тело можно представить (рис. 1б) как совокупность трёх сплошных цилиндров 1, 2 и 3 за вычетом двух малых дисков 4, расположенных на месте отверстий маховика.

Для расчёта момента инерции такого тела

(6)

необходимо знать массы указанных элементов, их радиусы, а также расстояние a от центра отверстий до оси вращения. В случае, если массы m_i неизвестны, то для их определения через плотность и объём деталей нужно измерить ещё их длины l₁, l₂ и l₃.

№ п.п.	Элемент тела вращения	Масса m, кг	Диаметр d, мм, и a, мм	Момент инерции I,кг×м 2
формула	значение
Диск
Вал–шкив
Ось
4а)	Кольцо
б)	Цилиндр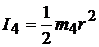
в)	Шар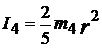
г)	Стержень
д)	Пластина	(bxd)
Тело		a=

а) значения I_i и I_с даны относительно оси, проходящей через центр масс;

б) для стержня длиной l и пластины размером b´dзначения I даны относительно оси, перпендикулярной их плоскости;

в) в формуле для I_с: n – число одинаковых элементов; знак «минус» для случая, если отверстия в диске имеют форму четвертого элемента.

3. Получите формулу вида (3.6) для расчёта момента инерции тела относительно оси, проходящей через центр масс системы.

4. Запишите в табл. 1 массы m_i отдельных частей тела, а если они неизвестны, то плотность вещества r.

5. Измерьте линейкой или штангенциркулем (в отчёте объясните выбор инструмента) величины, необходимые для расчёта момента инерции каждого элемента тела. Результаты измерений записывайте в табл. 1.

6. Вычислите моменты инерции отдельных элементов, а затем момент инерции тела I_с относительно оси, проходящей через центр масс.

7. Рассчитайте, если это необходимо в данной работе, момент инерции тела относительно МОВ, используя теорему Штейнера (3.5).

8. Оцените систематическую (приборную) погрешность прямых измерений (с. 7), сделанных для расчёта величины I. Результаты внесите в табл. 2.

Измеряемый параметр	Величина	Систематическая погрешность DS	Относительная погрешность d
di

9. В выводе оцените соотношение величин I_i частей тела. Какие из них пренебрежимо малы и по какой причине? По данным табл. 2 сделайте вывод о том, какие измерения проведены с достаточной точностью, а какие – нет; связано ли последнее с используемым инструментом?

Видео:Момент инерции абсолютно твердого тела. 10 класс.Скачать

Лабораторная работа №7 Определение момента инерции тела, скатывающегося с наклонной плоскости

Видео:Момент инерцииСкачать

Лабораторная работа №7

Видео:Зависимость углового ускорения от момента инерцииСкачать

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛА, СКАТЫВАЮЩЕГОСЯ С НАКЛОННОЙ ПЛОСКОСТИ

ЦЕЛЬ: приобрести навык расчёта момента инерции тел, состоящих из простых элементов, определить момент инерции тела относительно мгновенной оси враще­ния расчётным и экспериментальным методом

ОБОРУДОВАНИЕ: установка, набор тел, секундомер

Видео:Момент инерции абсолютно твердого тела. Практическая часть. 10 класс.Скачать

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

В работе используются тела, осью которых является цилиндрический стер­жень радиусом r. Одно из рис. 1) помещают на параллельные направ­ляющие 2, образующие с горизонтом углы α1 и α2.

Если тело отпустить, то оно, скатываясь, достигнет нижней точки и, двига­ясь далее по инерции, поднимется вверх по направляющим. Движение тела, при котором траектории всех точек лежат в параллельных плоскостях, называется плоским. Плоское движение можно представить двумя способами: либо как со­вокупность поступательного движения тела со скоростью центра масс и враща­тельного вокруг оси, проходящей через центр масс; либо как только враща­тельное движение вокруг мгновенной оси вращения (MOB), положение которой непрерывно изменяется. В нашем случае эта мгновенная ось Z проходит через точки касания направляющих с движущимся стержнем.

ОПИСАНИЕ МЕТОДА ИЗМЕРЕНИЙ

При скатывании тело, опускаясь с высоты проходит путь l0, а поднимаясь по инерции на высоту проходит путь l. В нижней точке скорость поступательного движения центра масс , а угловая скорость тела

, (1)

где t — время движения от верхней точки до нижней, г — радиус стержня (оси).

На скатывающееся тело действует момент сил сопротивления Мтр. Работа его на пути l0 равна A = Мтрφ где угловой путь φ = l0/r.

Закон сохранения энергии на отрезке пути l0 имеет вид

, (2)

где J — момент инерции скатывающегося тела относительно MOB, m — масса тела, включающая в себя массу стержня.

При движении тела вниз с высоты h0 и вкатывании его на высоту h работа сил сопротивления на пути (l + l0) равна убыли потенциальной энергии

. (3)

Запишем формулу для определения момента инерции динамическим методом:

(4)

Здесь величина (α1 и α2) является константой для данной установки.

Момент инерции тела относительно MOB определяется теоремой Штейнера J = J0 + ma2, (5)

где J0 — момент инерции, относительно центра масс; а — расстояние от центра масс тела до оси вращения (в этом опыте a = r).

Видео:5. Момент инерции простейших телСкачать

ПРАКТИЧЕСКАЯ ЧАСТЬ

Задание 1. Расчёт момента инерции тела сложной формы

Для расчёта момента инерции маховика I необходимо измерить массу тела (написана на телах) или объём (массу рассчитать, используя плотность) и ра­диусы цилиндрических тел.

1. Исследуйте форму тела. Приняв во внимание, что момент инерции любо­го тела равен сумме моментов инерции отдельных его элементов, мысленно разделите исследуемое тело на простые элементы, для которых формулы расчё­та величины Ji даны в табл. 1.

2. Сделайте эскиз исследуемого тела, а если необходимо, то и его элемен­тов, обозначая символами все размеры, подлежащие измерению. Например, те­ло (рис. 1а) состоит из насаженных на вал 1 шкива 2 и маховика 3 с двумя от­верстиями 4. Это тело можно представить (рис. 16) как совокупность трёх сплошных цилиндров 1, 2 и 3 за вычетом двух малых дисков расположенных на месте отверстий маховика.

Для расчёта момента инерции такого тела необходимо знать массы указанных элементов, их радиусы, а также расстояние а от центра отверстий до оси вращения.

(5)

В случае, если массы тi неизвестны, то для их определения через плотность и объём деталей нужно измерить ещё их длины l1, l2 и l3.

Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Лабораторная работа №6

Видео:Расчёт момента инерции тела относительно оси вращения. Момент инерции однородного стержняСкачать

ОПРЕДЕЛЕНИЕ момента инерции системы: маховое колесо – ось – вал динамическим методом

Фамилия И.О. _________________ Группа __________ Дата ______

Введение

В динамике вращательного движения твердого тела понятия “сила” и “масса” заменяются понятиями “момент силы” и “момент инерции”.

При вращении твердого тела вокруг некоторой оси эффект действия силы зависит не только от величины силы, но и от расстояния точки приложения силы до оси вращения. Поэтому вместо силы вводится момент силы, равный произведению величины действующей силы на плечо (кратчайшее расстояние от оси вращения до направления действующей силы)

Роль массы играет момент инерции. Свойство инертности во вращательном движении зависит не только от массы материальной точки, но и от расстояния этой точки до оси вращения.

Моментом инерции материальной точки называют произведение массы материальной точки на квадрат расстояния ее от оси вращения:

,

где m – масса материальной точки; r – расстояние материальной точки до оси вращения.

Так как тело состоит из множества точек и при вращении тела около некоторой оси каждая точка обладает некоторым моментом инерции относительно этой оси, то моментом инерции тела относительно этой оси вращения называют сумму моментов инерции всех материальных точек тела:

В этой работе ставится задача определения момента инерции системы, состоящей из махового колеса оси и вала.

Небольшое маховое колесо, которое может вращаться с очень малым трением около горизонтальной оси, расположено на высоте h ₀ от пола. Ось вращения проходит через центр тяжести махового колеса. На оси колеса находится небольшого диаметра вал, на который наматывается шнур (рис. 15).

Если к шнуру подвесить гирю массой m ₀, и закрутить вал так, чтобы гиря поднялась на высоту g , то гиря и вся система маховое колесо – ось – вал приобретут потенциальную энергию:

,

где m – масса гири , g – ускорение свободного падения , h – высота гири над полом.

Если отпустить гирю, то она начнет падать, раскручивая шнур и вращая всю систему.

Потенциальная энергия гири будет превращаться в кинетическую энергию падающей гири и вращающейся системы маховое колесо – ось – вал

.

Следовательно, пренебрегая трением, по закону сохранения энергии можно записать:

(33)

где — скорость падения гири в момент приземления,

— угловая скорость вращения системы в тот же момент,

-момент инерции системы маховое колесо – ось – вал.

Считая движение гири равноускоренным, можно написать:

где а – ускорение падения гири: t – вре6мя падения.

Следовательно, определив и подставив его значение в формулу скорости , получим

Линейная скорость вращения точки на внешней поверхности вала равна скорости падения гири. Связь между линейной и угловой скоростями вращения:

,

где r – радиус вала и или .Подставляем значения и в формулу (33):

.

(34)

I . Приборы и установка

В нашей лаборатории установка система маховое колесо – ось – вал смонтирована на кронштейне, который укреплен на стене (рис.15).

Шнур укреплен на валу. Установка имеет тормоз, с помощью которого гиря освобождается для падения.

При установке имеется 2 гири разных масс, метровая линейка или рулетка, секундомер и штангенциркуль.

II , Порядок выполнения работы

1. Измерить метровой линейкой или рулеткой с точностью до 1 см высоту поднятия гири от пола до нижней поверхности гири. Штангенциркулем измерить диаметр вала. Эти данные записать.

2. Снять гирю и взвесить на технико-химических весах с точностью до 0,5 г.

3. Повесить гирю на шнур и освободить маховое колесо от тормоза. В этот момент включить секундомер.

4. Гиря начнет падать, раскручивая вал и маховое колесо. В момент удара гири о пол выключить секундомер. Время падения записать.

5. Закручивая маховое колесо, поднять гирю на прежнюю высоту и повторить опыт, как сказано в пунктах 3-м и 4-м еще два-три раза.

Среднее арифметическое значение времени из этих измерений войдет в расчетную формулу (34).

6. Повторить опыт с другой гирей и сделать те же расчеты.

Подсчитать момент инерции системы маховое колесо – ось – вал по формуле (34).

Среднее арифметическое значение момента инерции из всех измерений принимается за значение момента инерции системы маховое колесо – ось – вал.

7. Вычислить относительную и абсолютную ошибки измерений.

Видео:Теория механизмов и машин. Лекция: динамические модели механизмов и определение их параметровСкачать

Определение момента инерции однородного шара динамическим методом Текст научной статьи по специальности « Физика»

Видео:Урок 93. Основное уравнение динамики вращательного движенияСкачать

Аннотация научной статьи по физике, автор научной работы — Сушкин К.Ю.

В статье рассматривается инерция однородного шара динамическим методом. Автор статьи ставит цель определить расчётную формулу для момента инерции однородного шара.

Видео:Принцип ДаламбераСкачать

Похожие темы научных работ по физике , автор научной работы — Сушкин К.Ю.

Видео:Механика Л9. 2022. Моменты инерции сферы и шара. Тензор момента инерции 1Скачать

Текст научной работы на тему «Определение момента инерции однородного шара динамическим методом»

3. Махмудов Б.М., Сокуров В.Ф. и др. Исследование функции пространственного распределения черенковского излучения ШАЛ на установке СамГУ. М.: Изв. АН СССР, Сер. физ., 1982. Т. 9.

4. Глушков А.В., Сокуров В.Ф. и др. Флуктуации продольного развития ШАЛ и состав первичного излучения с Ео > 1017 эВ. М.: Изв. АН СССР, Сер. физ., 1985. Т. 49. № 7.

5. Сокуров В.Ф. Физика космических лучей: космическая радиация. Ростов-н/Д.: Феникс, 2005.

6. Сокуров В.Ф. Проблемы физики сверхвысоких энергий. Рук. деп. в ВИНИТИ 6.05.93. № 1439-B93. 1993.

6. Сокуров В.Ф. Поток электромагнитных вспышек в приземном слое. Рук. деп. в ВИНИТИ 01.02.02. № 209-В2002.

8. Glushkov A.V., SokurovV.F. et al. The Cerenkov Radiation Densities. Proc. 16-th ICRC, Kyoto, 1979. vol. 8, p.156-160.

9. Efimov N.N., Sokurov V.F. Measurement of Spectrum of the EAS Cerenkov Radiation Densities. Proc.16-th ICRC, Kyoto, 1979. vol. 8, p.152-155.

10. Diminshtein O.S., Egorov T.A., Sokurov V.F. et al. Electrons and Muons in EAS with Given Primary Energy. Proc. 14-th ICRC, Munchen, 1975. vol. 12, p. 4318-4323.

11. Efimov N.N., Sokurov V.F. Density Spektrum of the EAS Cerenkov Radiation and Primary Energy Spektrum. Proc. 18-th ICCR, Bongolor, India, 1983. v. 2.

12. Glushkov A.V., Grigoriev V.M., Sokurov V.F. et al. Lateral Distribution and Total Flux of EAS Cerenkov Radiation with E ICCR, Paris, 1981. v. 12.

13. Христиансен Г.Б., Сокуров В.Ф.и др. Исследование структурной функции пространственного распределения черенковского излучения ШАЛ: Доклад на Всесоюзной конференции по космическим лучам. Самарканд, 1982.

14. Сокуров В.Ф. Исследование первичного энергетического спектра космических лучей в интервале 1015-1017 эВ и прозрачнасти атмосферы по спектру плотностей черенковского излучения ШАЛ // Диссертация на соиск. степ. канд. физ.-мат. наук. М., 1983. 141 c.

15. Сокуров В.Ф. Результаты исследования спектра плотностей черенковского излучения ШАЛ / Космические лучи с энергией выше 1017 эВ. Якутск: ЯФ СО АН СССР, 1983. C. 61-76.

16. Глушков А.В., Сокуров В.Ф. и др. Энергетический спектр космических лучей экстремальных энергий / Характеристики широких атмосферных ливней космических лучей сверхвысоких энергий. Якутск: Изд. ЯФ СО АН СССР, 1976. C. 45-86.

17. Сокуров В.Ф. Радиоизлучение ШАЛ экстремально высоких энергий в ОНЧ диапазоне / Широкие атмосферные ливни с энергией выше 1017 эВ. Якутск: Изд. ЯФ СО АН СССР, 1987. C. 45-86.

18. Сокуров В.Ф. Механизмы радиоизлучения ШАЛ в ОНЧ диапазоне. М., 1991. — Деп. в ВИНИТИ. № 4770-В91.

19. Сокуров В.Ф. Связь космических лучей сверхвысоких энергий с ОНЧ радиоизлучением. М., 1991. — Деп. в ВИНИТИ. № 4767-В91.

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ОДНОРОДНОГО ШАРА ДИНАМИЧЕСКИМ МЕТОДОМ

Если к телу, которое может вращаться около неподвижной оси, приложен вращающий момент относительно данной оси, то под его действием тело получает упругое угловое ускорение, то есть начинает вращаться. При этом вращающий момент М и угловое ускорение ¡5, связаны соотношением:

где I момент инерции тела относительно оси вращения, характеризует инертность тела во вращательном движении.

Момент инерции тела относительно данной оси вращения рассчитывается по формуле:

где mi — масса ьтой материальной точки тела, Г — расстояние ьтой материальной точки до оси вращения.

Если к телу приложен вращающий момент М , величина которого в процессе вращения остается постоянной, то вращение тела будет равноускоренным. Наблюдая равноускоренное вращения тела, под действием постоянного момента, и измеряя соответствующим образом угловое ускорение Р, можно определить момент инерции тела относительно оси вращения:

Ниже предлагается описание установки и динамического метода определения инерции однородного шара. Однородный шар 1 (смотрите рисунок) жестко укреплён на валу 2. Вал может вращаться в подшипниках 3 с малым трением около горизонтальной оси. Ось вращения проходит через центр тяжести шара, через один из его диаметров. На валу шара также жестко закреплен плексигласовый шкив 4. В шкиве имеется маленькое отверстие для продевания капроновой нити 5; нить наматывается в несколько оборотов на шкив. На свободный конец нити подвешивается груз Р, приводящий всю систему в равноускоренное движение. Также крепится сантиметровая линейка.

Под действием груза Р на маховик будет действовать вращающий момент М , равный

произведению силы натяжения нити р на плечо = —, то есть:

Где d — диаметр шкива 4.

Если груз действует на нить с силой Р , то нить действует с силой Р и в соответствии с третьим законом Ньютона эти силы равны по величине и противоположны по направлению, то есть:

Для определения силы Р рассмотрим движение груза вниз. На груз действуют две силы: со стороны Земли — mg (вес груза Р), и со стороны нити Р. Под действием этих сил груз будет двигаться равноускоренно с ускорением а. Согласно второму закону Ньютона имеем:

где т — масса груза. Отсюда, в проекции на вертикальную координатную ось, получим:

где g — ускорение силы тяжести.

Вращающий момент М с учётом (4) и (6) определяется выражением

Тогда момент инерции однородного шара на основании (2), равен:

где Р — угловое ускорение однородного шара и шкива. Угловое ускорение шкива /? и тангенциальное ускорение ат точек, лежащих на его ободе, связаны следующим образом:

Понятно, что тангенциальное ускорение С1Т с которым вращаются точки лежащие на ободе шкива (нить, накручена на шкив) и линейное ускорение а с которым опускается груз равны

Величину линейного ускорения а можно выразить из закона пути для равноускоренного

где Н — высота с которой опускается груз.

С учётом (10) и (9) окончательно получим расчётную формулу для момента инерции одно родного шара:

💡 Видео

Моменты инерции сечения из простых фигурСкачать

Урок 97. Теорема ШтейнераСкачать

Расчет момента инерции тонкого стержняСкачать

Моменты силы, импульса, инерции. Динамика вращательного движенияСкачать

Лекция 06 Динамика твердого телаСкачать

Урок 79. Центр масс тела и методы определения его положенияСкачать

Динамические уравнения ЭйлераСкачать