Исследование объективно существующих связей между явлениями — важнейшая задача статистики. В процессе статистического исследования зависимостей выявляются причинно-следственные отношения между явлениями. Причинно-следственные отношения — это такая связь явлений и процессов, когда изменение одного из них — причины ведет к изменению другого — следствия.
Признаки явлений и процессов по их значению для изучения взаимосвязи делятся на два класса. Признаки, обуславливающие изменения других, связанных с ними признаков, называют факторными, или просто факторами. Признаки, изменяющиеся под действием факторных признаков, называют результативными.
В статистике различают функциональные и стохастические (вероятностные) связи явлений и процессов:
- Функциональной называют такую связь, при которой определенному значению факторного признака соответствует одно значение результативного.
- Если причинная зависимость проявляется не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений, то такая зависимость называется стохастической (вероятностной). Частным случаем стохастической связи является корреляционная связь.
Кроме того, связи между явлениями и их признаками классифицируются по степени тесноты, направлению и аналитическому выражению.
По направлению выделяют связь прямую и обратную:
- Прямая связь — это такая связь, при которой с увеличением (уменьшением) значений факторного признака происходит увеличение (уменьшение) значений результативного. Так, например, рост производительности труда способствует увеличению уровня рентабельности производства.
- В случае обратной связи значения результативного признака изменяются под воздействием факторного, но в противоположном направлении по сравнению с изменением факторного признака. Так с увеличением уровня фондоотдачи снижается себестоимость единицы производимой продукции.
По аналитическому выражению выделяют связи прямолинейные (или просто линейные) и нелинейные:
- Если статистическая связь между явлениями может быть приблизительно выражена уравнением прямой линии, то ее называют линейной связью вида: у=а+bх.
- Если же связь может быть выражена уравнением какой-либо кривой линии (параболы, гиперболы и др.), то такую связь называют нелинейной (криволинейной) связью.
Теснота связи показывает меру влияния факторного признака на общую вариацию результативного признака. Классификация связи по степени тесноты представлена в таблице 1.
| Величина коэффициента корреляции | Характер связи |
|---|---|
| До ±3 | Практически отсутствует |
| От ±3 до ±0,5 | Слабая |
| От ±0,5 до ±0,7 | Умеренная |
| От ±0,7 до ±1,0 | Сильная |
Для выявления наличия связи, ее характера и направления в статистике используются следующие методы: приведения параллельных данных, аналитических группировок, графический, корреляции. Основным методом изучения статистической взаимосвязи является статистическое моделирование связи на основе корреляционного и регрессионного анализа.
Корреляция — это статистическая зависимость между случайными величинами, не имеющая строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой. В статистике принято различать следующие виды корреляции:
- парная корреляция — связь между двумя признаками (результативным и факторным, или двумя факторными);
- частная корреляция — зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков;
- множественная корреляция — зависимость результативного и двух или более факторных признаков, включенных в исследование.
Задачей корреляционного анализа является количественное определение тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи).
Теснота связи количественно выражается величиной коэффициентов корреляции, которые давая количественную характеристику тесноты связи между признаками, позволяют определять «полезность» факторных признаков при построении уравнения множественной регрессии.
Корреляция взаимосвязана с регрессией, поскольку первая оценивает силу (тесноту) статистической связи, вторая исследует ее форму.
Регрессионный анализ заключается в определении аналитического выражения связи в виде уравнения регрессии.
Регрессией называется зависимость среднего значения случайной величины результативного признака от величины факторного, а уравнением регрессии – уравнение описывающее корреляционную зависимость между результативным признаком и одним или несколькими факторными.
Формулы корреляционно-регрессионного анализа для прямолинейной связи при парной корреляции представлены в таблице 2.
| Показатель | Обозначение и формула |
|---|---|
| Уравнение прямой при парной корреляции | yx = a +bx, где b — коэффициент регрессии |
| Система нормальных уравнений способом наименьших квадратов для определения коэффициентов a и b | 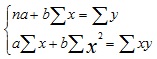 |
| Линейный коэффициент корреляции для определения тесноты связи, его интерпретация: r = 0 – связь отсутствует; 0 2012 © Лана Забродская. При копировании материалов сайта ссылка на источник обязательна Содержание Видео:Математика #1 | Корреляция и регрессияСкачать  Тест по статистике с ответами 1 курсКакие два основных элемента имеется в таблице? 2. Какие существуют виды статистических таблиц? 3. Как называется график,созданный на основании накопленных частот? 4. Какое максимальное значение кумуляты? 5. Сколько показателей существует в составе абсолютных величин? 6. В консервной промышленности емкость банки, равной 353,4 см3, 7. Что такое относительная величина в статистике? 8. В чем выражается относительная величина структуры? 9. Что характеризуют относительные величины динамики? 10. По какой формуле можно рассчитать относительную величину структуры? 11. Какое основополагающе условие для применения средних величин? 12. Когда применяется средняя арифметическая взвешенная? 13. Как рассчитать величину средней арифметической способом моментов? 14. Что называется модой? 15. Что такое медианный интервал? 16. Какие существую виды уравнения прямолинейной и криволинейной связи? 17. Как обозначается коэффициент детерминации? 18. На основе какой шкалы даётся качественная оценка полученному коэффициенту корреляции? 19. Сколько существуют видов дисперсий? 20. Какой из видов дисперсии отражает случайную вариацию? 21. Сколько существует видов рядов динамики? 22. Какие основные показатели имеются в каждом ряду динамики? 23. Какие существуют способы сопоставления показателей динамики? 24. Что такое темп роста в статистике? 25. Что характеризует типичную величину абсолютных уровней? 26. На основе какой взаимосвязи можно определить средний темп прироста? 27. Сколько существует основных методов в статистике для получения данных об общих тенденциях развития? 28. Как называется метод в основу которого положено определение по исходным данным теоретических уровней, в которых случайные 29. Что такое центрирование? 30. Как определяется индекс сезонности? Видео:Математика это не ИсламСкачать  Прямая и обратная связьПо направлению различают прямую и обратную связь. Если с увеличением аргумента х функция у также увеличивается без всяких единичных исключений, то такая связь называется полной прямой связью. Если с увеличением аргументам функция у уменьшается без всяких единичных исключений, то такая связь называется полной обратной. Кроме того, в виде исключений, которые, однако, не нарушают общей тенденции, встречается частичная связь — прямая или обратная. Когда признаки варьируют независимо друг от друга, говорят о полном отсутствии связи. Видео:Коэффициент корреляции. Статистическая значимостьСкачать  Прямолинейная и криволинейная связьПо аналитическому выражению корреляционная связь может быть прямолинейной и криволинейной. Прямолинейной называется связь, когда величина явления изменяется приблизительно равномерно в соответствии с изменением величины влияющего фактора. Математически прямолинейная связь может быть выражена уравнением прямой: которое называется линейным уравнением регрессии. Если происходит неравномерное изменение явления в связи с изменением величины влияющего фактора, то такая связь называется криволинейной. Математически криволинейная зависимость может быть выражена уравнением криволинейной связи. В экономическом анализе для ее выражения часто пользуются уравнением параболы второго порядка: Уравнение криволинейной связи может быть выражено и в виде дробной функции: показательной функции: Однако корреляционные связи могут быть выражены лишь приблизительно, в то время как функциональные связи имеют точное аналитическое выражение. 🎬 ВидеоЭконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать  Химия | Молекулярные и ионные уравненияСкачать  Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать  ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать  Теория вероятностей #13: виды ПРВ: гауссовая, равномерная, рэлея, экспоненциальнаяСкачать  КОРРЕЛЯЦИЯ Спирмена Пирсона Кенделла | АНАЛИЗ ДАННЫХ #12Скачать  Эконометрика Линейная регрессия и корреляцияСкачать  Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать  Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать  КОРРЕЛЯЦИЯ Спирмена Пирсона STATISTICA #08Скачать  Корреляционный анализСкачать  §31.1 Приведение уравнения кривой к каноническому видуСкачать  Эконометрика. Множественная регрессия и корреляция.Скачать  Коэффициент корреляции, уравнение прямой регрессии, элементы математической статистикиСкачать  Корреляционно-регрессионный анализ. Функциональная и корреляционная связиСкачать  Удалили с экзамена ОГЭ Устное Собеседование shorts #shortsСкачать  Статистика # 12. Исследование связи между ранжируемыми качественными признакамиСкачать  |