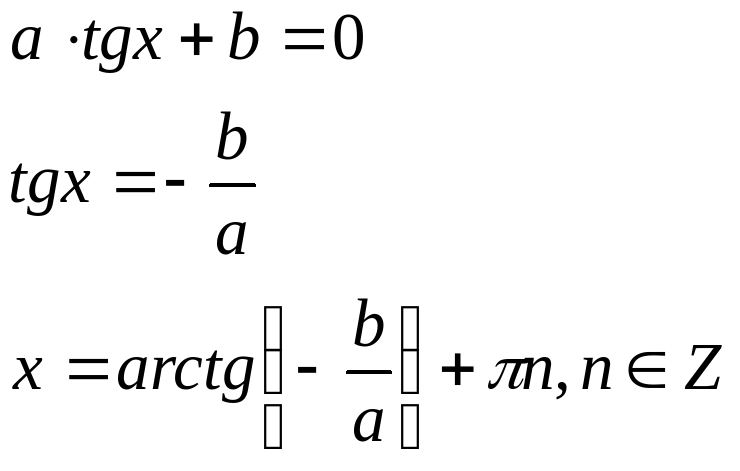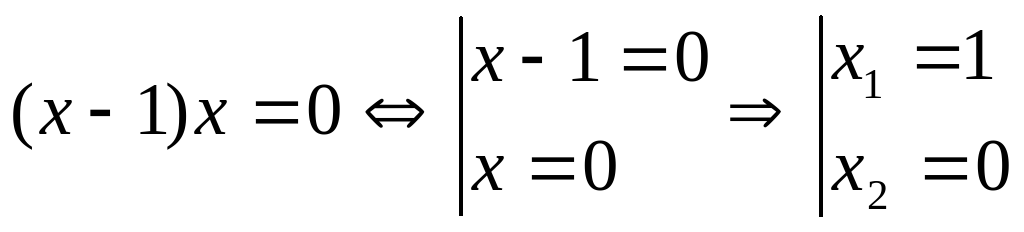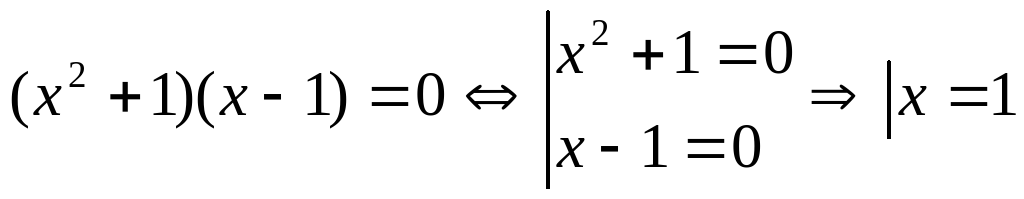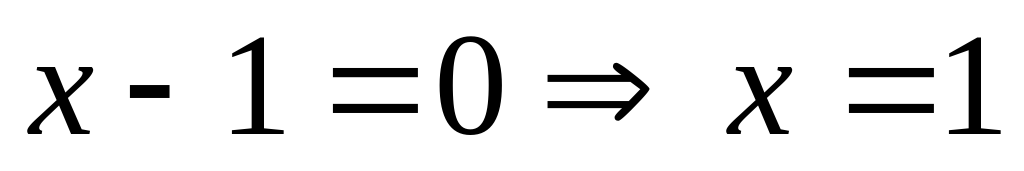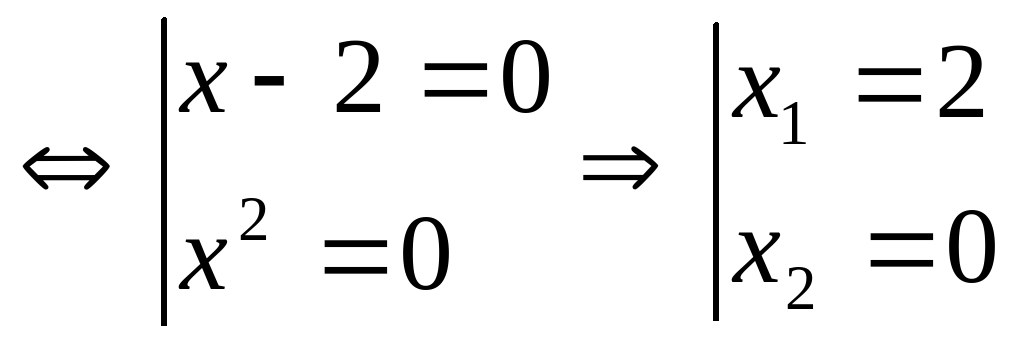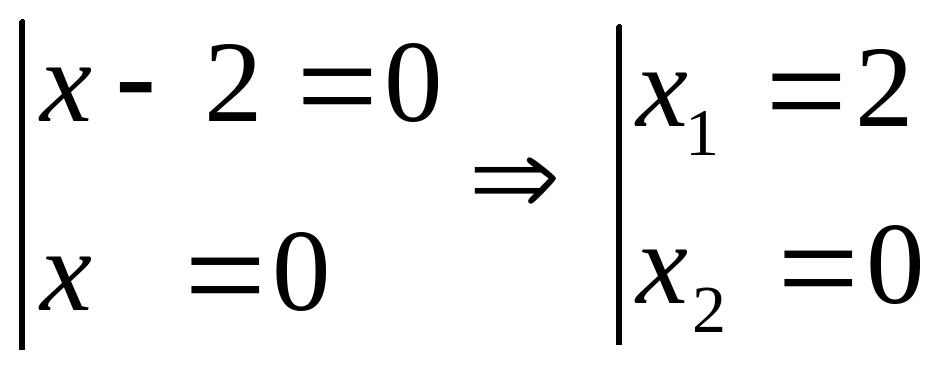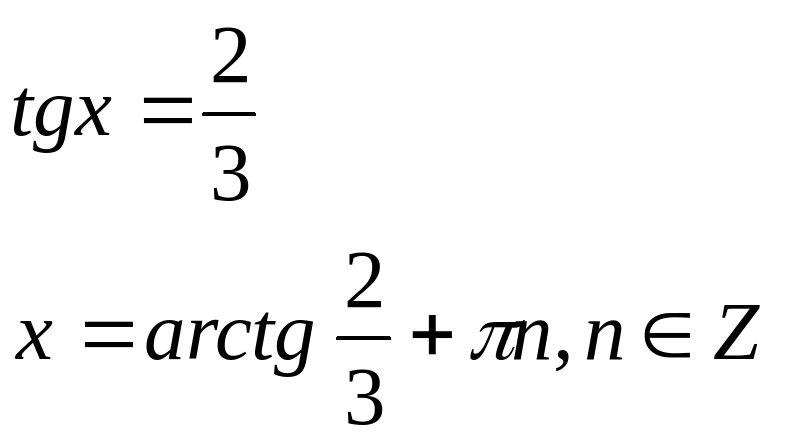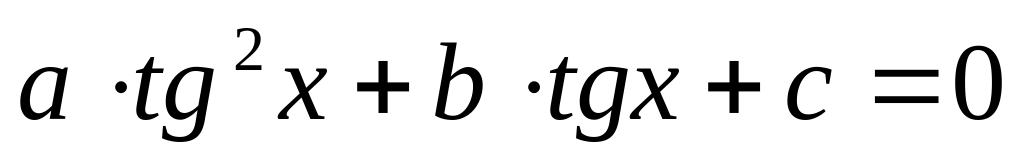Какие слагаемые могут содержаться в однородных тригонометрических уравнениях первой степени

Видео:Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать

Алгебра и начала анализа. Урок по теме «Однородные тригонометрические уравнения» (10-й класс)

Разделы: Математика

Класс: 10

• ввести понятие однородных тригонометрических уравнений I и II степени ;
• сформулировать и отработать алгоритм решения однородных тригонометрических уравнений I и II степени;
• научить учащихся решать однородные тригонометрических уравнений I и II степени;
• развивать умение выявлять закономерности, обобщать;
• стимулировать интерес к предмету, развивать чувство солидарности и здорового соперничества.

Тип урока: урок формирования новых знаний.

Форма проведения: работа в группах.

Оборудование: компьютер, мультимедийная установка

I. Организационный момент

Приветствие учащихся, мобилизация внимания.

На уроке рейтинговая система оценки знаний (учитель поясняет систему оценки знаний, заполнение оценочного листа независимым экспертом, выбранным учителем из числа учащихся). Урок сопровождается презентацией . Приложение 1.

II. Актуализация опорных знаний..

Домашняя работа проверяется и оценивается независимым экспертом и консультантами до урока и заполняется оценочный лист.

Учитель подводит итог выполнения домашнего задания.

Учитель: Мы продолжаем изучение темы “Тригонометрические уравнения”. Сегодня на уроке мы познакомимся с вами с еще одним видом тригонометрических уравнений и методами их решения и поэтому повторим изученное. Все виды тригонометрических уравнений при решении сводятся к решению простейших тригонометрических уравнений.

Проверяется индивидуальное домашнее задание, выполняемое в группах. Защита презентации “Решения простейших тригонометрических уравнений”

(Оценивается работа группы независимым экспертом)

III. Мотивация обучения.

Учитель: нам предстоит работа по разгадыванию кроссворда. Разгадав его, мы узнаем название нового вида уравнений, которые научимся решать сегодня на уроке.

Вопросы спроецированы на доску. Учащиеся отгадывают, независимый эксперт заносит в оценочный лист баллы отвечающим учащимся.

Разгадав кроссворд, ребята прочитают слово “однородные”.

IV. Усвоение новых знаний

Учитель: Тема урока “Однородные тригонометрические уравнения”.

Запишем тему урока в тетрадь. Однородные тригонометрические уравнения бывают первой и второй степени.

Запишем определение однородного уравнения первой степени. Я на примере показываю решение такого вида уравнения, вы составляете алгоритм решения однородного тригонометрического уравнения первой степени.

Уравнение вида аsinx + bcosx = 0 называют однородным тригонометрическим уравнение первой степени.

Рассмотрим решение уравнения, когда коэффициенты а и в отличны от 0.

Пример: sinx + cosx = 0

Разделив обе части уравнения почленно на cosx, получим

Внимание! Делить на 0 можно лишь в том случае, если это выражение нигде не обращается в 0. Анализируем. Если косинус равен 0, то получается и синус будет равен 0, учитывая что коэффициенты отличны от 0, но мы знаем, что синус и косинус обращаются в нуль в различных точках. Поэтому эту операцию производить можно при решении такого вида уравнения.

Алгоритм решения однородного тригонометрического уравнения первой степени:

• Деление обеих частей уравнения на cosx, cosx 0

Уравнение вида аsin mx + bcos mx = 0 тоже называют однородным тригонометрическим уравнение первой степени и решат также деление обеих частей уравнения на косинус mх.

Уравнение вида a sin 2 x + b sinx cosx + c cos2x = 0 называют однородным тригонометрическим уравнением второй степени.

Пример: sin 2 x + 2sinx cosx – 3cos 2 x = 0

Коэффициент а отличен от 0 и поэтому как и предыдущем уравнении соsх не равен0 и поэтому можно воспользоваться способом деления обеих частей уравнения на соs 2 х.

Получим tg 2 x + 2tgx – 3 = 0

Решаем путем введения новой переменной пусть tgx = а , тогда получаем уравнение

Возвращаемся к замене

Ответ:

Если коэффициент а = 0, то уравнение примет вид 2sinx cosx – 3cos 2 x = 0 решаем способом вынесения общего множителя cosx за скобки

Если коэффициент с = 0, то уравнение примет вид sin 2 x +2sinx cosx = 0

решаем способом вынесения общего множителя sinx за скобки .

Алгоритм решения однородного тригонометрического уравнения первой степени:

1. Посмотреть, есть ли в уравнении член asin 2 x.
2. Если член asin 2 x в уравнении содержится (т.е. а 0), то уравнение решается делением обеих частей уравнения на cos 2 x и последующим введение новой переменной.
3. Если член asin 2 x в уравнении не содержится (т.е. а = 0), то уравнение решается методом разложения на множители: за скобки выносят cosx.

Однородные уравнения вида a sin 2 m x + b sin mx cos mx + c cos 2 mx = 0 решаются таким же способом

Алгоритм решени однородных тригонометрических уравнений записан в учебнике на стр. 102.

V. Формирование навыков решения однородных тригонометрических уравнений

Открываем задачники стр. 53

1-я и 2-я группа решают № 361 в)

3-я и 4-я группа решают № 363 в)

Показывают решение на доске, объясняют, дополняют. Независимый эксперт оценивает.

Решение примеров из задачника

№ 361в)
sinx – 3cosx = 0
делим обе части уравнения на cosx 0, получаем

№ 363в)
sin 2 x + sinxcosx – 2cos 2 x = 0
разделим обе части уравнения на cos 2 x, получим
tg 2 x + tgx – 2 = 0
решаем путем введения новой переменной
пусть tgx = а , тогда получаем уравнение
а 2 + а – 2 = 0
Д = 9
а₁ = 1 а₂ = –2
возвращаемся к замене

VI. Самостоятельная работа

1. 2 cosx – 2 = 0
2. tg2x +1 = 0
3. 2cos 2 x – 3cosx +1 = 0
4. 3 sin 2 x + sinx cosx – 2 cos 2 x = 0

По окончанию самостоятельной работы меняются работами и взаимопроверка. Правильные ответы проецируются на доску.

Потом сдают независимому эксперту.

Решение самостоятельной работы

VII. Подведение итогов урока

1. С каким видом тригонометрических уравнений мы познакомились на уроке?
2. Алгоритм решения тригонометрических уравнений первой и второй степени.

VIII. Задание на дом

§ 20.3 читать. № 361(г), 363(б), повышенной трудности дополнительно

Если вписать верные слова, то получится название одного из видов тригонометрических уравнений.

1. Значение переменной, обращающее уравнение в верное равенство? (Корень)
2. Единица измерения углов? (Радиан)
3. Числовой множитель в произведении? (Коэффициент)
4. Раздел математики, изучающий тригонометрические функции? (Тригонометрия)
5. Какая математическая модель необходима для введения тригонометрических функций? (Окружность)
6. Какая из тригонометрических функций четная? (Косинус)
7. Как называется верное равенство? (Тождество)
8. Равенство с переменной? (Уравнение)
9. Уравнения, имеющие одинаковые корни? (Равносильные)
10. Множество корней уравнения? (Решение)

Рейтинговая система оценки знаний

• Домашнее задание – 12 баллов (на дом было задано 3 уравнения 4 х 3 = 12)
• Презентация – 1балл
• Активность уч-ся – 1ответ – 1 балл (4 балла максимально)
• Решение уравнений 1 балл
• Самостоятельная работа – 4 балла

“5” – 22 балла и более
“4” – 18 – 21 балл
“3” – 12 – 17 баллов

За высокую активность ставится дополнительная оценка.

Видео:Как решать однородные тригонометрические уравненияСкачать

Однородные тригонометрические уравнения

Однородные тригонометрические уравнения. теория и прмеры решения уравнений

Просмотр содержимого документа
«Однородные тригонометрические уравнения»

Однородные тригонометрические уравнения

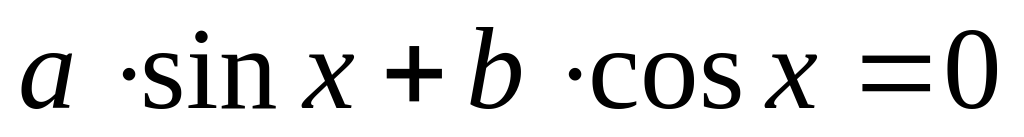
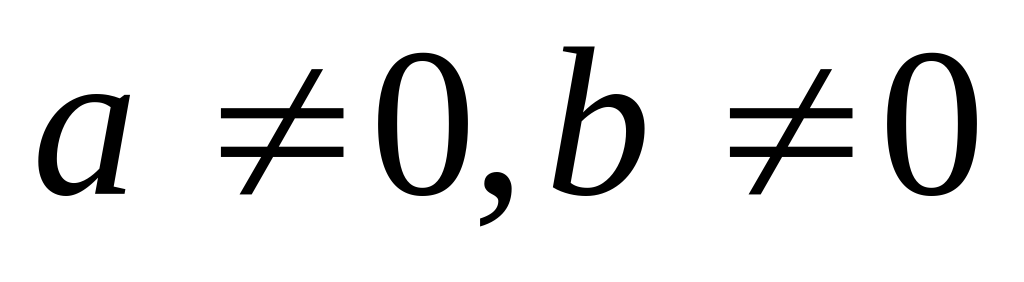
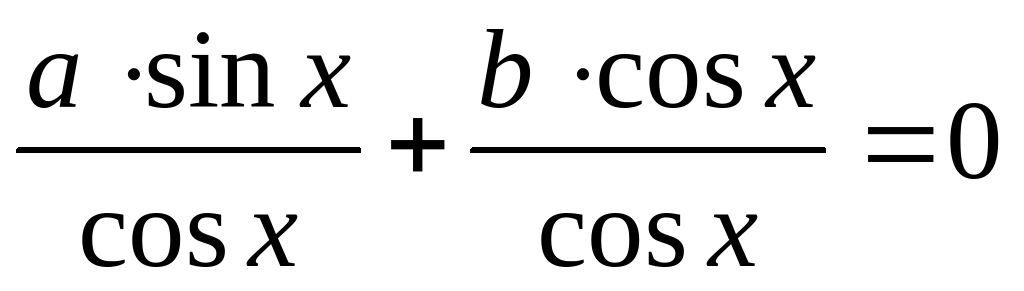
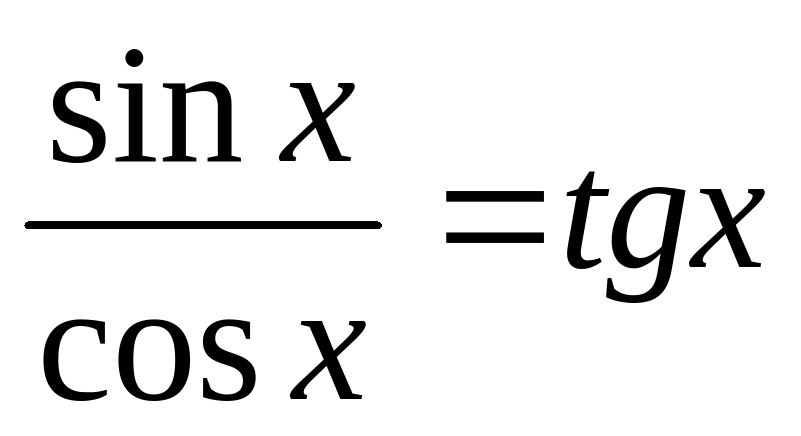
Тригонометрическое уравнение вида , где , называется однородным тригонометрическим уравнением первой степени. Для его решения достаточно обе части уравнения разделить на cosx:

, учитывая, что , получаем:

Замечание «О потере корней»

При проведении почленного деления на функцию возможна потеря корней. Рассмотрим примеры.

Решим уравнение (х-1)х=0 двумя способами:

Решение: 1 способ:

2 способ: разделим уравнение на (х-1). Получим: х=0.

Как видим во втором случае мы потеряли корень х=1. Его можно восстановить, если приравнять к нулю функцию, на которую проводилось деление, и, прорешать полученное уравнение: х-1=0, значит х=1

Решим уравнение 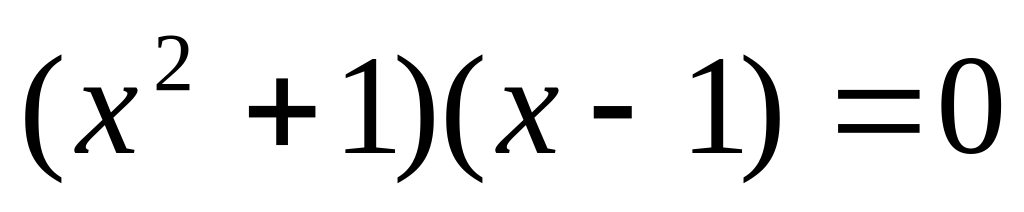двумя способами.

Решение: 1 способ:

2 способ: Разделим уравнение на 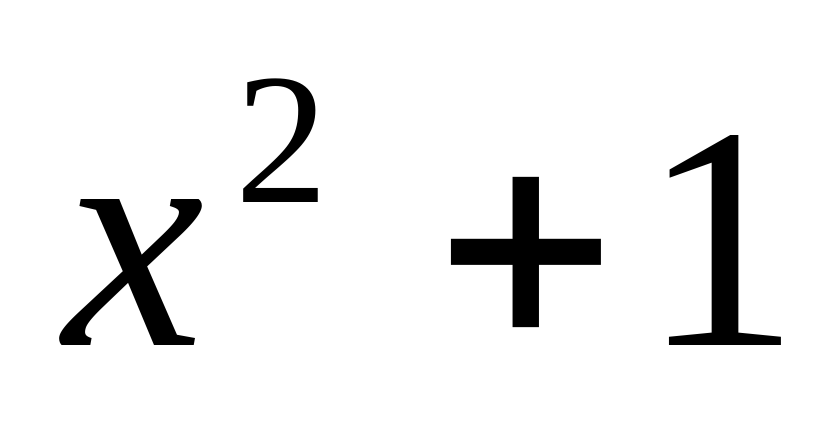, получим

Как видим во втором примере потери корней нет, так как уравнение 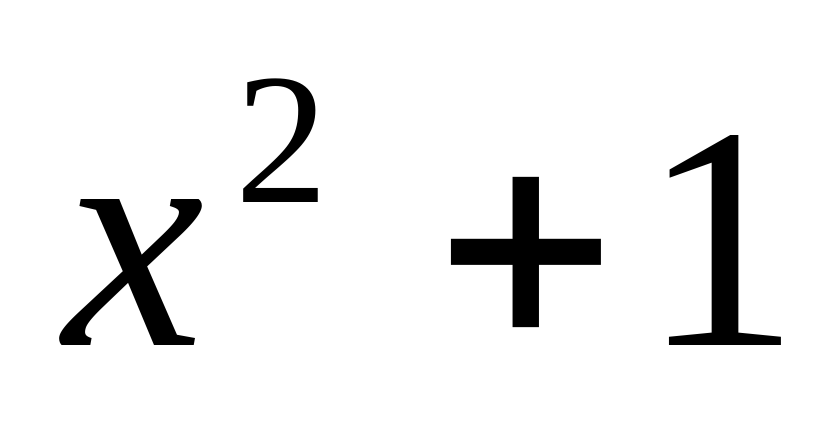=0 не имеет решений.

Вернемся теперь к решению нашего тригонометрического уравнения. Следует заметить, что при делении на cosx потери корней нет, не смотря на то, что уравнение cosx=0 имеет решения! Действительно, те значения х, при которых выполняется равенство cosx=0 не удовлетворяют данному тригонометрическому уравнению, в силу того, что в противном случае выполнялось бы также равенство sinх =0, а sinx и cosx одного и того же аргумента не могут быть равны нулю одновременно.

Решим уравнение 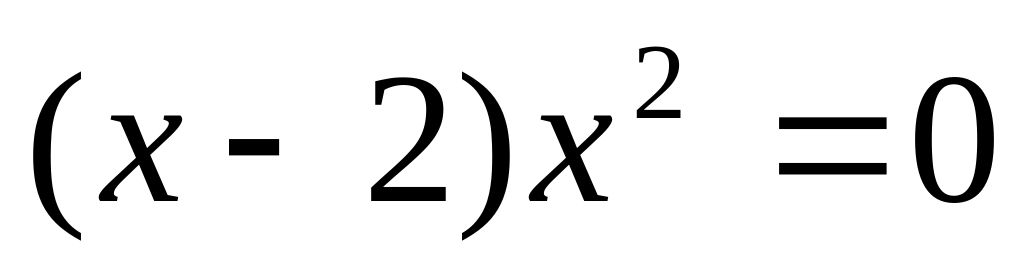двумя способами

Решение: 1 способ: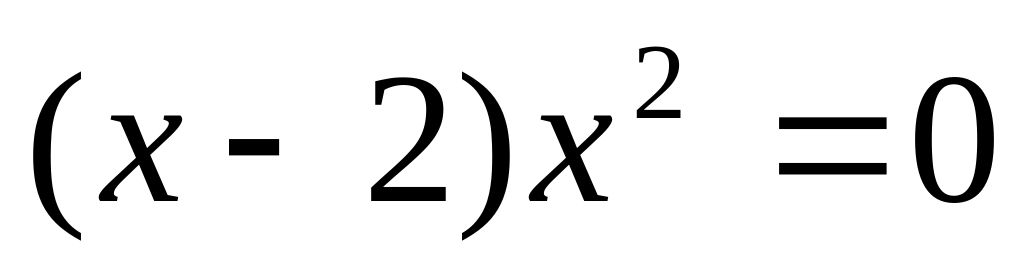

2 способ: Разделим уравнение на х, получим,(х-2)х=0. Это уравнение равносильно совокупности двух уравнений:

Как видим в этом примере потери корней нет., так как мы провели деление на х, а х=0 – является корнем уравнения, который найден в процессе решения исходного уравнения.

При решении уравнений методом почленного деления возможна потеря корней. Чтобы установить имела ли место потеря корней необходимо приравнять к нулю функцию, на которую производилось деление, найти корни полученного уравнения и подставить их в исходное уравнение. Если найденные корни являются корнями исходного уравнения, и не были установлены в процессе его решения, то эти корни были потеряны в процессе деления и их необходимо включить в ответ. Если же полученное уравнение не имеет корней или имеет корни, которые не являются корнями исходного уравнения, или являются корнями исходного уравнения, но были установлены в процессе его решения, то в этом случае потери корней нет…

Решить уравнение: 3sinx-2cosx=0

Решение: это однородное тригонометрическое уравнение первой степени. Разделим обе части на cosx, получим ,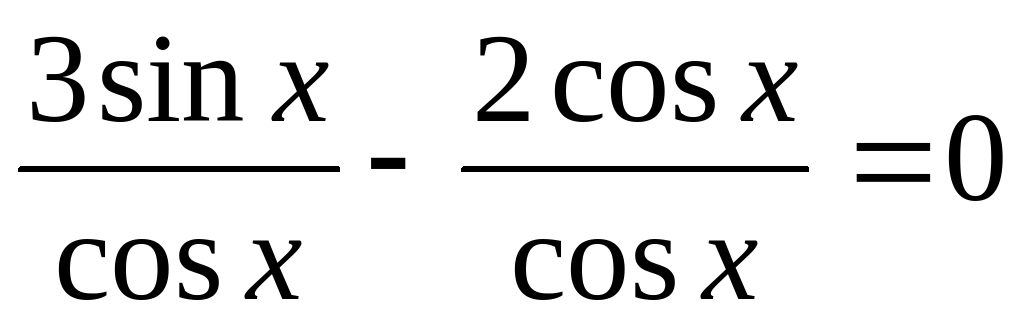

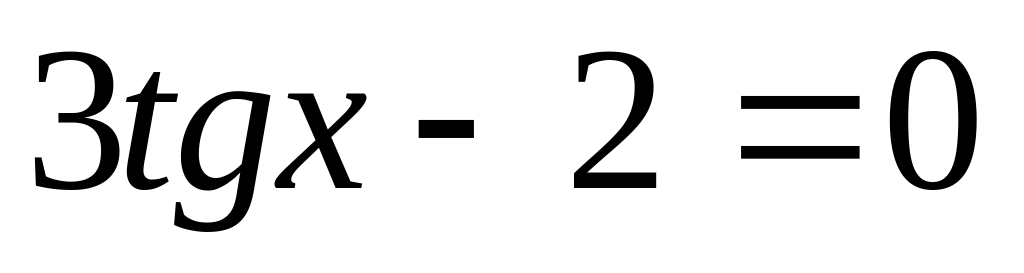
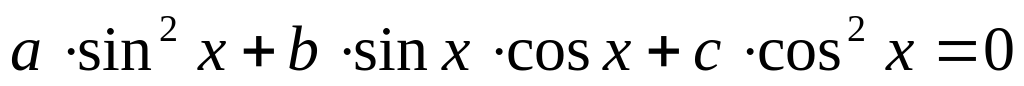
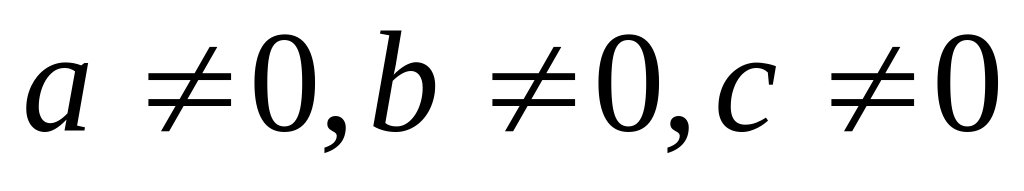
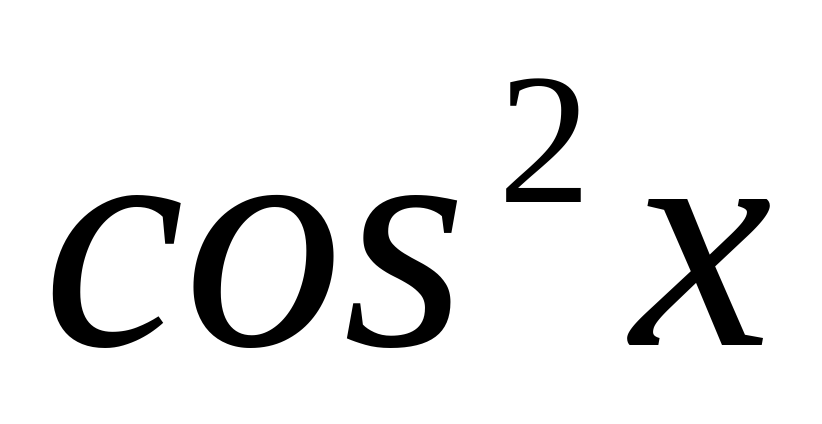
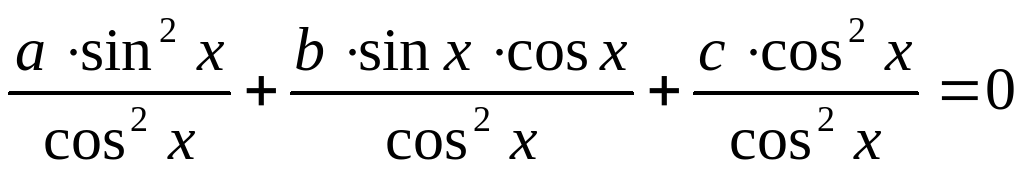
Определение. Тригонометрическое уравнение вида , где ,называется однородным тригонометрическим уравнением второй степени. Для его решения достаточно обе части уравнения разделить на :

,

Получили квадратное уравнение относительно tgx.

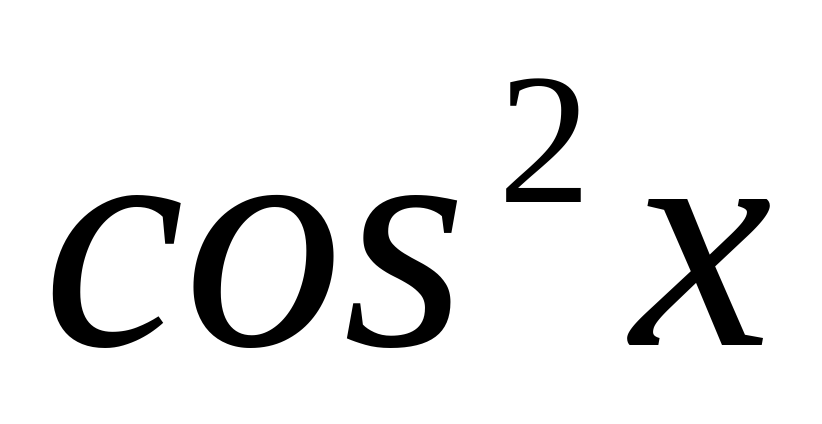
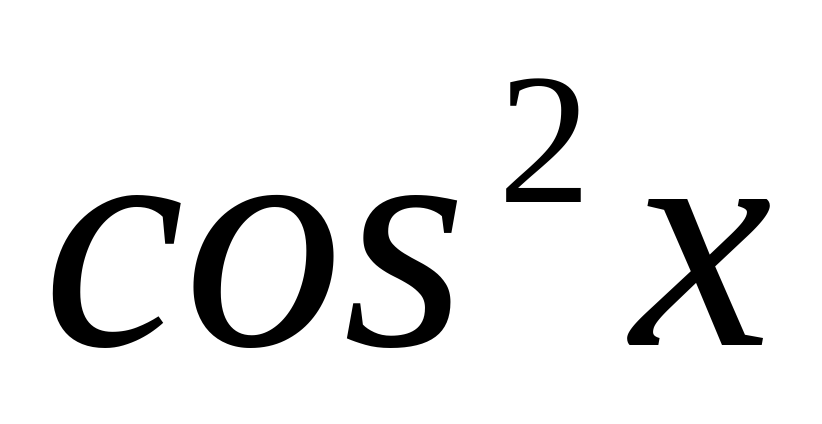
Следует заметить, что при делении на потери корней нет, так как те значения х, при которых выполняется равенство =0 не удовлетворяют исходному уравнению в силу того, что в противном случае выполнялось бы также равенство sinx=0, чего быть не может (sinx и cosx не равны нулю одновременно).

Данное уравнение равносильно уравнению . Получили однородное тригонометрическое уравнение второй степени. Разделим уравнение на 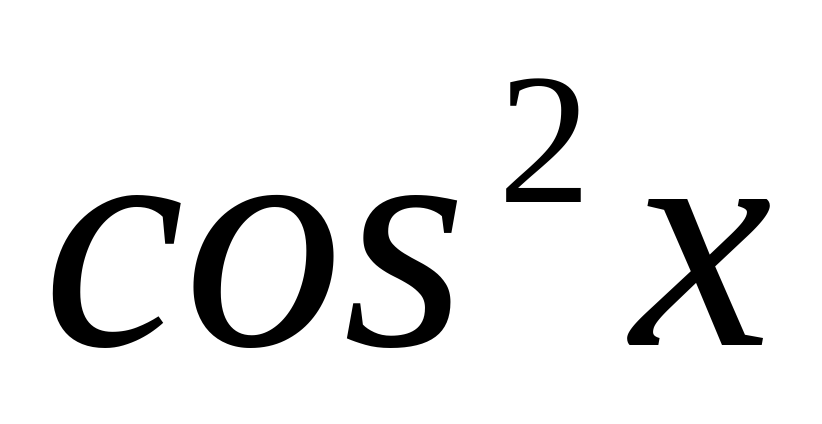, получим:

Сделаем замену переменной: tgx=t, получим квадратное уравнение:

Корнями этого уравнения являются:

Обратная замена: 1)

Решение: Применяя формулу синуса двойного аргумента, получим:

. Получили однородное тригонометрическое уравнение второй степени. Разделим уравнение на :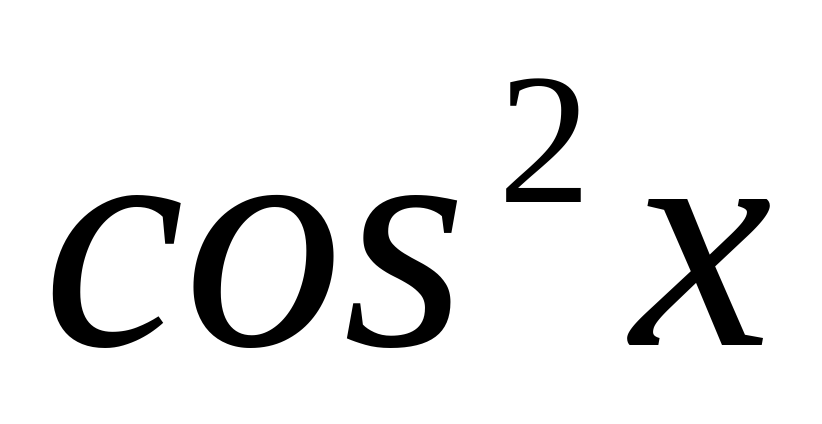

. Пусть , получаем квадратное уравнение: . Корни этого уравнения:

Решение: Применяя формулу синуса двойного угла и основное тригонометрическое тождество, , получаем:

Выполнив преобразования, получим:

. Получили однородное тригонометрическое уравнение второй степени. Делим это уравнение на :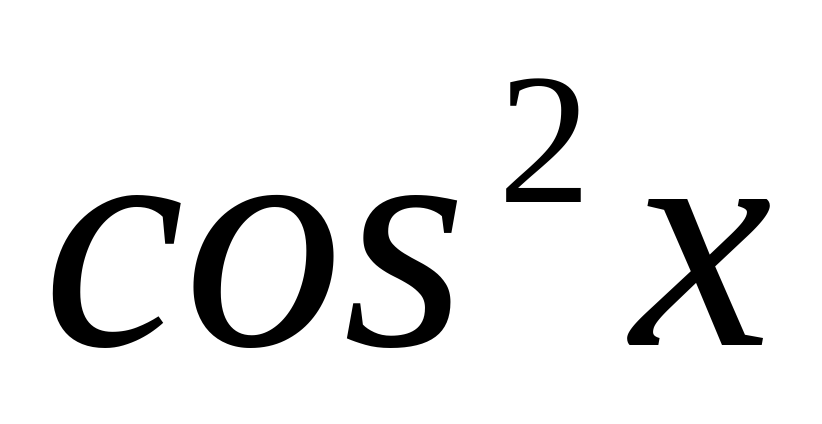

Видео:3A Однородные тригонометрические уравнения первой степениСкачать

Уравнение. Однородные тригонометрические уравнения относительно sin и cos.

Уравнение считаются однородным относительно sin и cos, когда все его члены одинаковой степени относительно sin и cos и одинакового угла.

Рассмотрим несколько примеров однородных тригонометрических уравнений:

sin 2 х — 5 sin х cos х + 6 cos 2 х = 0,

cos 2 х — sin х cos х = 0.

К примеру, у членов первого уравнения общая степень 1, а у членов других двух уравнений — общая степень 2

Для решения подобных уравнений требуется:

— переместить все его компоненты в левую часть;

— переместить общие множители за скобки;

— приравнять все множители и скобки к нулю;

— скобки, равные нулю, дают однородное уравнение меньшей степени, которое необходимо поделить на cos ( или sin ) в большей степени;

— найти корни образовавшегося уравнения относительно tg ( или ctg)..

Найдем корни уравнения sin х — cos х = 0.

В рассматриваемом варианте cos x не допустимо приравнять к нулю. Если допустить что cos х = 0, то тогда и sin х = 0. И в таком случаем не осуществилось бы соотношение sin 2 х +cos 2 х = 1. Значит, в этом выражении cos х ≠ 0.

Следовательно, обе части указанного выражения можем поделить на cos 2 х. Тогда получим tg x — 1 = 0, далее:

Сходным образом решаем и уравнение sin 2 х — 5 sin х cos х + 6 cos 2 х = 0.

Поделим обе части этого выражения на cos 2 х:

tg 2 х — 5 tg х + 6 = 0;

Видео:Однородные тригонометрические уравнения II степени. Видеосправочник по математике #4Скачать

x = arctg 2 + nπ х = arctg 3 + kπ .

Вычислим корни уравнения cos 2 х — sin х cos х = 0.

В этом случае тождество cos х = 0 допустимо, и следовательно, поделить обе части выражения на cos 2 х невозможно. Однако, возможно, что sin х ≠ 0. В противоположном случае из выражения получалось бы, что cosх = 0. Но тогда не осуществилось бы равенство sin 2 х +cos 2 х = 1. Итак, sin х ≠ 0. Значит обе части данного выражения возможно поделить на sin 2 х.

После проведения преобразований имеем:

Согласно этому формируются две группы корней:

Некоторые тригонометрические уравнения, не будучи однородными, просто преобразуются в однородные.

Так, когда в уравнении:

представим 0,5 как 0,5 (sin 2 х +cos 2 х), и получим однородное уравнение sin х cos x = 0,5 sin 2 х + 0,5 cos 2 х.

🎬 Видео

Тригонометрические однородные уравнения | МатематикаСкачать

10й класс; Математика; Однородные тригонометрические уравнения I, II степениСкачать

Алгебра 10 класс (Урок№46 - Однородные тригонометрические уравнения.)Скачать

Однородные тригонометрические уравнения. Общие понятия. √3 sinxcosx+3cos^2 x=0Скачать

Однородные тригонометрические уравненияСкачать

Однородные тригонометрические уравненияСкачать

10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Однородные тригонометрические уравненияСкачать

Однородное уравнение 1 СТЕПЕНИСкачать

Однородные тригонометрические уравненияСкачать

Однородные тригонометрические уравнения. Часть 13.11. Алгебра 10 классСкачать

Щелчок по математике I №5,6,12 Тригонометрия с нуля и до ЕГЭ за 4 часаСкачать

Однородные тригонометрические уравненияСкачать

Однородные тригонометрические уравнения I степени. Видеосправочник по математике #3Скачать

Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

Подготовка к ЕГЭ #87. Решение однородных тригонометрических уравненийСкачать