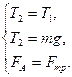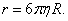Какие силы действуют на шарик в жидкости напишите уравнение движения шарика (8 видео)

Содержание

Рассмотрим падение шарика в вязкой жидкости
Теория метода и описание установки
Какие силы действуют на шарик в жидкости напишите уравнение движения шарика
Лабораторная работа №1 «Исследование движения тел в диссипативной среде»
💡 Видео

Видео:Урок 137. Движение тела в жидкости и газе.Скачать

Рассмотрим падение шарика в вязкой жидкости

При движении шарика слой жидкости, граничащий с его поверхностью, прилипает к шарику и движется со скоростью шарика. При вычислении сопротивления среды следует учитывать трение отдельных слоев жидкости друг о друга, а не трение шарика о жидкость.

На шарик, падающий в вязкой жидкости, действуют три силы (рис. 2.2):

· сила тяжести F₁= mg = p_ш×V×g;

· сила Архимеда F_А = p_ж×V×g (равная весу жидкости в объеме шарика);

· сила сопротивления, обусловленная вязкостью жидкости:

F = 6p×h×r×v,

где r_ш – плотность материала шарика;

r_ж – плотность жидкости;

V – объем шарика;

g – ускорение свободного падения.

Все три силы направлены по вертикали: F₁ – вниз, F₂ и F₃ – вверх.

В общем случае уравнение движения шарика имеет вид

Сила сопротивления с увеличением скорости движения шарика возрастает, а ускорение dv/dt уменьшается до тех пор, пока шарик не достигнет такой скорости, при которой ускорение равно 0.

Тогда уравнение (2.3) примет вид:

в этом случае шарик движется с постоянной скоростью v₀.

Решая (2.4) относительно h, получим

(2.5)

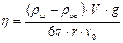
Если теперь учесть, что V = r 3 , r = d/2, v₀ = l/t,

где d – диаметр шарика;

l – длина участка равномерного движения, пройденного за время t,

то формула (2.5) примет окончательный вид

(2.6)

Таким образом, для нахождения h нужно измерить d, l и t.

Рассмотрим подъем шарика в вязкой жидкости.

Если два одинаковых шарика связаны невесомой нитью, перекинутой через блок, причем один из шариков будет погружен в сосуд с жидкостью (2.3.), то уравнения движения шарика имеют вид:

(2.7)

В уравнениях (2.7)

I – момент инерции диска;

R – радиус диска;

Т₁ и Т₂ – натяжение нитей,

F_тр – сила трения, обусловленная вязкостью жидкости,

F_А – сила Архимеда.

Сила сопротивления с увеличением скорости движения шарика возрастает, а ускорение уменьшается до тех пор, пока шарик не достигнет такой скорости v₀, при которой ускорение равно 0.

Тогда уравнения (2.7), при , принимают вид:

В этом случае шарик двигается с постоянной скоростью. Из (2.8) следует

(2.9)

или аналогично формуле (2.6) расчетная формула принимает вид:

(2.10)

В формуле (2.10) так же как и в формуле (2.6) нужно измерить d, l, t.

Описание установки.

Длинный стеклянный цилиндр, наполненный исследуемой жидкостью, имеет две горизонтальные метки А и В, расположенные на расстоянии l друг от друга. Метка А установлена так, что при прохождении через нее шарик уже имеет постоянную скорость v₀ (см. рис 2.2).

При измерении вязкости при подъеме шарика применяется схема (рис. 2.3): на краю стеклянного цилиндра установлен блок, через который перекинуты шарики, связанные нитью. Для определения вязкости при подъеме шарика, один шарик опускают на дно цилиндра с жидкостью.

Видео:Механика. Л 5.5. Силы в жидкости.Скачать

Теория метода и описание установки

Метод Стокса, используемый в данной работе, заключается в следующем.

На твердый шарик, падающий в вязкой жидкости, действуют три силы: сила тяжести, выталкивающая и сила сопротивления движению, обусловленная силами внутреннего трения жидкости (рисунок 2).

Рисунок 2. Силы, действующие на шарик, падающий в жидкости

При движении шарика слой жидкости, граничащий с его поверхностью, прилипает к шарику и движется со скоростью шарика. Ближайшие смежные слои жидкости также приводятся в движение, но получаемая ими скорость тем меньше, чем дальше они находятся от шарика.

Сила внутреннего трения по закону Стокса равна:

где — коэффициент внутреннего трения жидкости, — скорость шарика, — его радиус.

Сила тяжести равна:

где — плотность вещества шарика, — объем шарика.

Выталкивающая сила (по закону Архимеда) равна:

где — плотность жидкости.

Указанные три силы направлены по вертикали: сила тяжести — вниз, выталкивающая сила и сила трения — вверх.

На основании второго закона Ньютона уравнение движения в случае падения шарика в жидкости имеет вид:

закон вязкость сопротивление

Сила сопротивления с увеличением скорости движения шарика возрастает, а ускорение уменьшается и, наконец, шарик достигает такой скорости, при которой ускорение становится равным нулю, тогда уравнение (5) принимает вид:

В этом случае шарик движется с постоянной скоростью . Такое движение шарика называется установившимся. Решая уравнение (6) относительно коэффициента внутреннего трения, получим

Формула (7) справедлива для шарика, падающего в безгранично простирающейся жидкости. Практически невозможно осуществить падение шарика в безграничной среде, так как жидкость всегда находится в каком-то сосуде, имеющем стенки. Если шарик падает вдоль оси цилиндрического сосуда радиуса , то учет наличия стенок приводит к следующему выражению для коэффициента вязкости:

Наличие таких границ жидкости, как дно сосуда и верхняя поверхность жидкости, этой формулой не учитывается.

Выполнение работы и обработка результатов измерений

1. Измерить диаметр шариков с помощью микроскопа с окулярным микрометром. Для этого шарик положить на предметное стекло и поместить под микроскоп. Сфокусировав микроскоп, произвести отсчет делений окулярного микрометра.
2. Пинцетом опустить шарик в цилиндр с жидкостью как можно ближе к его оси; глаз наблюдателя должен быть при этом установлен против верхней метки на цилиндре с жидкостью. В момент прохождения шарика через эту метку пустить в ход секундомер. После этого глаз поместить против второй метки и в момент прохождения шарика через нее остановить секундомер. Опыт проделать с тремя шариками.
3. Определить скорости шариков по формуле:

где l — расстояние между двумя метками, t — время падения шарика.

4. Подставляя в формулу (8) значения , а также и , найти величину коэффициента внутреннего трения для каждого шарика.
5. Результаты измерений и вычислений занести в таблицу.

6. Определить среднее значение для коэффициента внутреннего трения.
7. Оценить доверительный интервал среднего результата по формуле (для доверительной вероятности 0,95):

8. Окончательный результат представить в виде:

1. Что такое вязкость? В каких единицах измеряется коэффициент вязкости?
2. Какие силы действуют на шарик, падающий в жидкости?
3. Сформулируйте закон Стокса.
4. Почему, начиная с некоторого момента времени шарик, начинает двигаться равномерно?
5. Как изменяется скорость движения шарика с увеличением его диаметра?

Видео:Шарик в мертвой петле.Скачать

Какие силы действуют на шарик в жидкости напишите уравнение движения шарика

Лабораторная работа № 204

ОПРЕДЕЛЕНИЕ ВЯЗКОСТИ ЖИДКОСТИ МЕТОДОМ СТОКСА

Цель работы: изучить метод Стокса, определить коэффициент динамической вязкости глицерина.

Приборы и принадлежности:

стеклянный цилиндрический сосуд с глицерином,

1. ВЯЗКОСТЬ ЖИДКОСТИ. ЗАКОН СТОКСА

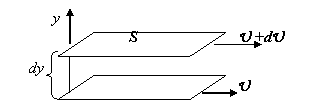
В жидкостях и газах при перемещении одних слоев относительно других возникают силы внутреннего трения, или вязкости, которые определяются законом Ньютона:

(1)

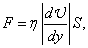
где h — коэффициент внутреннего трения, или коэффициент динамической вязкости, или просто вязкость; 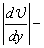модуль градиента скорости, равный изменению скорости слоев жидкости на единицу длины в направлении нормали (в нашем случае вдоль оси y ) к поверхности S соприкасающихся слоев (рис. 1).

Согласно уравнению (1) коэффициент вязкости h в СИ измеряется в Па × с или в кг/( м × с ).

Механизм внутреннего трения в жидкостях и газах неодинаков, т.к. в них различен характер теплового движения молекул. Подробное изложение вязкости жидкости рассмотрено в работе № 203, вязкости газов – в работе № 205.

Вязкость жидкости обусловлена молекулярным взаимодействием, ограничивающим движение молекул. Каждая молекула жидкости находится в потенциальной яме, создаваемой соседними молекулами. Поэтому молекулы жидкости совершают колебательные движения около положения равновесия, то есть внутри потенциальной ямы. Глубина потенциальной ямы незначительно превышает среднюю кинетическую энергию, поэтому, получив дополнительную энергию при столкновении с другими молекулами, она может перескочить в новое положение равновесия. Энергия, которую должна получить молекула, чтобы из одного положения перейти в другое, называется энергией активации W , а время нахождения молекулы в положении равновесия – временем «оседлой жизни» t . Перескок молекул между соседними положениями равновесия является случайным процессом. Вероятность того, что такой перескок произойдет за время одного периода t ₀ , в соответствии с законом Больцмана, составляет

(2)

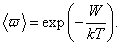
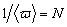
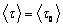
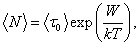
Величина, обратная вероятности перехода молекулы определяет среднее число колебаний, которое должна совершить молекула, чтобы покинуть положение равновесия. Среднее время «оседлой жизни» молекулы . Тогда

(3)

где k – постоянная Больцмана; 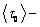средний период колебаний молекулы около положения равновесия.

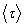
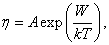
Коэффициент динамической вязкости зависит от : чем реже молекулы меняют положение равновесия, тем больше вязкость. Используя модель скачков молекул, советский физик Я.И.Френкель показал, что вязкость изменяется по экспоненциальному закону:

(4)

где А – константа, определяемая свойствами жидкости.

Формула (4) является приближенной, но она достаточно хорошо описывает вязкость жидкости, например, воды в интервале температур от 5 до 100 ° С, глицерина – от 0 до 200 ° С.

Из формулы (4) видно, что с уменьшением температуры вязкость жидкости возрастает. В ряде случаев она становится настолько большой, что жидкость затвердевает без образования кристаллической решетки. В этом заключается механизм образования аморфных тел.

При малых скоростях движения тела в жидкости слой жидкости, непосредственно прилегающий к телу, прилипает к нему и движется со скоростью тела. По мере удаления от поверхности тела скорость слоев жидкости будет уменьшаться, но они будут двигаться параллельно. Такое слоистое движение жидкости называется ламинарным. При больших скоростях движения жидкости ламинарное движение жидкости становится неустойчивым и сменяется турбулентным, при котором частицы жидкости движутся по сложным траекториям со скоростями, изменяющимися беспорядочным образом. В результате происходит перемешивание жидкости и образуются вихри.

Характер движения жидкости определяется безразмерной величиной Re , называемой числом Рейнольдса. Это число зависит от формы тела и свойств жидкости. При движении шарика радиусом R со скоростью U в жидкости плотностью r _ж

(5)

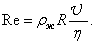
При малых Re ( — 2 мм движется со скоростью 5 — 10 см/ c в вязкой жидкости, например в глицерине, движение жидкости будет ламинарным. В этом случае на тело будет действовать сила сопротивления, пропорциональная скорости

(6)

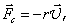
где r – коэффициент сопротивления. Для тела сферической формы

Сила сопротивления шарика радиусом R примет вид:

(7)

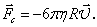
Формула (7) называется законом Стокса.

2. ОПИСАНИЕ РАБОЧЕЙ УСТАНОВКИ И МЕТОДА

Одним из существующих методов определения коэффициента динамической вязкости является метод Стокса. Суть метода заключается в следующем. Если в сосуд с жидкостью бросить шарик плотностью большей, чем плотность жидкости ( r > r _ж ), то он будет падать (рис. 2). На движущийся в жидкости шарик действует сила внутреннего трения (сила сопротивления) , тормозящая его движение и направленная вверх. Если считать, что стенки сосуда находятся на значительном расстоянии от движущегося шарика, то величину силы внутреннего трения можно определить по закону Стокса (6).

Видео:Определение коэффициента вязкости жидкости. Проверка закона СтоксаСкачать

Лабораторная работа №1 «Исследование движения тел в диссипативной среде»

Лабораторная работа №1 «Исследование движения тел в диссипативной среде»

1. Какие параметры характеризуют исследуемую систему как диссипативную? От каких величин зависит коэффициент сопротивления движению тела в диссипативной среде?

2. Дайте определения динамической, кинематической вязкости и текучести жидкости, а также ее ламинарного и турбулентного течения.

3. Как зависит сила сопротивления движению шарика в жидкости от скорости при малых и больших скоростях его движения.

4. Сделайте рисунок и укажите на нем все силы, действующие на шарик, падающий в жидкости.

5. Используя обозначения сил, указанных на рисунке, напишите уравнение движения шарика (второй закон Ньютона) в диссипативной среде для момента касания шариком поверхности жидкости. Напишите уравнение, описывающее движение шарика в жидкости в нестационарном и стационарном режиме.

6. Выведите (или докажите подстановкой в уравнение движения) зависимости скорости и ускорения шарика от времени в нестационарном режиме.

7. Используя выражения для сил п. 3, напишите уравнение движения шарика в стационарном режиме. Используя это уравнение, получите выражение для вязкости жидкости через радиус шарика.

8. Объясните различный характер температурной зависимости вязкости жидкостей и газов.

9. Чем обусловлена необходимость учета присоединенной массы?

10. Обоснуйте, почему в данной работе для обработки данных косвенных измерений нельзя применять метод переноса погрешностей, но возможно применение выборочного метода.

11. Запишите уравнение движения для тела, движущегося в однородном силовом поле в диссипативной среде, и объясните физический смысл величин, входящих в это уравнение.

12. Какие силы действуют на тело, падающее в вязкой среде?

13. Почему при ламинарном течении происходит изменение скорости слоев жидкости.? Приведите примеры движения тел в вязкой среде и укажите направление изменения скорости.

14. Какие параметры характеризуют исследуемую систему как диссипативную?

15. Дайте определение времени релаксации. Как определить время релаксации, пользуясь графиком переходного процесса в диссипативной системе?

16. От каких величин зависит коэффициент сопротивления движению в диссипативной среде?

17. Сформулируйте законы Ньютон. Как они реализуются в данной работе?

18. Что такое установившаяся скорость?

19. Почему при движении тела в вязкой среде под действием постоянной силы существует предельная скорость движения? Есть ли такая скорость при сухом трении?

20. Какой физический смысл коэффициента внутреннего трения (вязкости)?

21. В каких единицах измеряется коэффициент вязкости?

22. Что определяет формула Стокса?

23. Какие системы называются диссипативными?

24. Напишите уравнение динамики для шарика, опущенного в масло с достаточно большой скоростью. Получите зависимость скорости и ускорения шарика от времени.

25. Чем обусловлена сила сопротивления движению в вязкой среде? Как направлена эта сила?

26. Какие параметры влияют на силу сопротивления движению в вязкой среде?

27. Объясните суть явления вязкого трения.

28. Объясните превращение энергии при движении шарика в диссипативной среде.

29. Запишите аналитическое выражение и объясните уравнение баланса энергии на участке установившегося движения.

30. Напишите аналитическую формулу зависимости скорости движения тела от времени при движении в диссипативной среде в случае, когда начальная скорость нулевая.

31. Нарисуйте график зависимости скорости шарика от времени для двух случаев, когда в системе действуют сопротивления и когда — нет.

32. Напишите аналитическую формулу для ускорения шарика и определите a0 .

33. Нарисуйте теоретический график зависимости скорости шарика от времени при движении в диссипативной среде. Объясните вид этого графика.

34. Нарисуйте теоретический график зависимости ускорения шарика от времени при движении в диссипативной среде. Объясните вид этого графика.

35. Что такое присоединенная масса?

36. Как зависит коэффициент динамической вязкости от температуры?

37. От каких параметров зависит сила Архимеда?

38. Как по графику зависимости скорости шарика от времени определить мгновенное ускорение и путь, пройденный шариков за время t ?

39. Сравните потенциальные энергии аэростатов: парящего свободно и удерживаемого тросом у на одном уровне у поверхности Земли?

40. Два шарика, сделанные из одного материала, имеющие одинаковый радиус двигаются с одинаковой скоростью. Один из шариков полый. Сравните силы сопротивления, действующие на шарики?