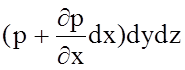Какие параметры жидкости связывает основное дифференциальное уравнение гидростатики (2 видео)

Какие параметры жидкости связывает основное дифференциальное уравнение гидростатики

Гидравлика делится на два раздела: гидростатика и гидродинамика. Гидродинамика является более обширным разделом и будет рассмотрена в последующих лекциях. В этой лекции будет рассмотрена гидростатика.

Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практическое применение.

В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением. Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна.

Рассмотрим резервуар с плоскими вертикальными стенками, наполненный жидкостью (рис.2.1, а). На дно резервуара действует сила P равная весу налитой жидкости G = γ V, т.е. P = G.

Если эту силу P разделить на площадь дна S_abcd, то мы получим среднее гидростатическое давление, действующее на дно резервуара.

Гидростатическое давление обладает свойствами.

Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости.

Для доказательства этого утверждения вернемся к рис.2.1, а. Выделим на боковой стенке резервуара площадку S_бок (заштриховано). Гидростатическое давление действует на эту площадку в виде распределенной силы, которую можно заменить одной равнодействующей, которую обозначим P. Предположим, что равнодействующая гидростатического давления P, действующая на эту площадку, приложена в точке А и направлена к ней под углом φ (на рис. 2.1 обозначена штриховым отрезком со стрелкой). Тогда сила реакции стенки R на жидкость будет иметь ту же самую величину, но противоположное направление (сплошной отрезок со стрелкой). Указанный вектор R можно разложить на два составляющих вектора: нормальный R_n (перпендикулярный к заштрихованной площадке) и касательныйR_τ к стенке.

Сила нормального давления R_n вызывает в жидкости напряжения сжатия. Этим напряжениям жидкость легко противостоит. Сила R_τ действующая на жидкость вдоль стенки, должна была бы вызвать в жидкости касательные напряжения вдоль стенки и частицы должны были бы перемещаться вниз. Но так как жидкость в резервуаре находится в состоянии покоя, то составляющая R_τ отсутствует. Отсюда можно сделать вывод первого свойства гидростатического давления.

Свойство 2. Гидростатическое давление неизменно во всех направлениях.

В жидкости, заполняющей какой-то резервуар, выделим элементарный кубик с очень малыми сторонами Δx, Δy, Δz (рис.2.1, б). На каждую из боковых поверхностей будет давить сила гидростатического давления, равная произведению соответствующего давления P_x, P_y , P_z на элементарные площади. Обозначим вектора давлений, действующие в положительном направлении (согласно указанным координатам) как P’_x, P’_y, P’_z, а вектора давлений, действующие в обратном направлении соответственно P»_x, P»_y, P»_z. Поскольку кубик находится в равновесии, то можно записать равенства

где γ — удельный вес жидкости;
Δx, Δy, Δz — объем кубика.

Сократив полученные равенства, найдем, что

Членом третьего уравнения γΔz, как бесконечно малым по сравнению с P’_z и P»_z, можно пренебречь и тогда окончательно

Вследствие того, что кубик не деформируется (не вытягивается вдоль одной из осей), надо полагать, что давления по различным осям одинаковы, т.е.

Это доказывает второй свойство гидростатического давления.

Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве.

Это положение не требует специального доказательства, так как ясно, что по мере увеличения погружения точки давление в ней будет возрастать, а по мере уменьшения погружения уменьшаться. Третье свойство гидростатического давления может быть записано в виде

Рассмотрим распространенный случай равновесия жидкости, когда на нее действует только одна массовая сила — сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке рассматриваемого объема жидкости. Это уравнение называется основным уравнением гидростатики.

Пусть жидкость содержится в сосуде (рис.2.2) и на ее свободную поверхность действует давление P₀ . Найдем гидростатическое давление P в произвольно взятой точке М, расположенной на глубине h. Выделим около точки М элементарную горизонтальную площадку dS и построим на ней вертикальный цилиндрический объем жидкости высотой h. Рассмотрим условие равновесия указанного объема жидкости, выделенного из общей массы жидкости. Давление жидкости на нижнее основание цилиндра теперь будет внешним и направлено по нормали внутрь объема, т.е. вверх.

Запишем сумму сил, действующих на рассматриваемый объем в проекции на вертикальную ось:

Последний член уравнения представляет собой вес жидкости, заключенный в рассматриваемом вертикальном цилиндре объемом hdS. Силы давления по боковой поверхности цилиндра в уравнение не входят, т.к. они перпендикулярны к этой поверхности и их проекции на вертикальную ось равны нулю. Сократив выражение на dS и перегруппировав члены, найдем

Полученное уравнение называют основным уравнением гидростатики. По нему можно посчитать давление в любой точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления P₀ на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости.

Из основного уравнения гидростатики видно, что какую бы точку в объеме всего сосуда мы не взяли, на нее всегда будет действовать давление, приложенное к внешней поверхности P₀. Другими словами давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости по всем направлениям одинаково. Это положение известно под названием закона Паскаля.

Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня (подробно рассмотрим в п.2.6). В обычных условиях поверхности уровня представляют собой горизонтальные плоскости.

Пусть мы имеем резервуар с наклонной правой стенкой, заполненный жидкостью с удельным весом γ. Ширина стенки в направлении, перпендикулярном плоскости чертежа (от читателя), равна b (рис.2.3). Стенка условно показана развернутой относительно оси АВ и заштрихована на рисунке. Построим график изменения избыточного гидростатического давления на стенку АВ.

Так как избыточное гидростатическое давление изменяется по линейному закон P=γgh, то для построения графика, называемого эпюрой давления, достаточно найти давление в двух точках, например А и B.

Избыточное гидростатическое давление в точке А будет равно

Соответственно давление в точке В:

где H — глубина жидкости в резервуаре.

Согласно первому свойству гидростатического давления, оно всегда направлено по нормали к ограждающей поверхности. Следовательно, гидростатическое давление в точке В, величина которого равна γH, надо направлять перпендикулярно к стенке АВ. Соединив точку А с концом отрезка γH, получим треугольную эпюру распределения давления АВС с прямым углом в точке В. Среднее значение давления будет равно

Если площадь наклонной стенки S=bL, то равнодействующая гидростатического давления равна

где hc = Н/2 — глубина погружения центра тяжести плоской поверхности под уровень жидкости.

Однако точка приложения равнодействующей гидростатического давления ц.д. не всегда будет совпадать с центром тяжести плоской поверхности. Эта точка находится на расстоянии l от центра тяжести и равна отношению момента инерции площадки относительно центральной оси к статическому моменту этой же площадки.

где J_Аx — момент инерции площади S относительно центральной оси, параллельной Аx.

В частном случае, когда стенка имеет форму прямоугольника размерами bL и одна из его сторон лежит на свободной поверхности с атмосферным давлением, центр давления ц.д. находится на расстоянии b/3 от нижней стороны.

Пусть жидкость заполняет резервуар, правая стенка которого представляет собой цилиндрическую криволинейную поверхность АВС (рис.2.4), простирающуюся в направлении читателя на ширину b. Восстановим из точки А перпендикуляр АО к свободной поверхности жидкости. Объем жидкости в отсекеАОСВ находится в равновесии. Это значит, что силы, действующие на поверхности выделенного объема V, и силы веса взаимно уравновешиваются.

Представим, что выделенный объем V представляет собой твердое тело того же удельного веса, что и жидкость (этот объем на рис.2.4 заштрихован). Левая поверхность этого объема (на чертеже вертикальная стенка АО) имеет площадь Sx = bH, являющуюся проекцией криволинейной поверхности АВС на плоскостьyOz.

С правой стороны на отсек будет действовать реакция R цилиндрической поверхности. Пусть точка приложения и направление этой реакции будут таковы, как показано на рис.2.4. Реакцию R разложим на две составляющие R_x и R_z.

Из действующих поверхностных сил осталось учесть только давление на свободной поверхности Р₀. Если резервуар открыт, то естественно, что давление Р₀ одинаково со всех сторон и поэтому взаимно уравновешивается.

На отсек АВСО будет действовать сила собственного веса G = γV, направленная вниз.

Спроецируем все силы на ось Ох:

Теперь спроецируем все силы на ось Оz:

Составляющая силы гидростатического давления по оси O_y обращается в нуль, значит R_y = F_y = 0.

Таким образом, реакция цилиндрической поверхности в общем случае равна

а поскольку реакция цилиндрической поверхности равна равнодействующей гидростатического давленияR=F, то делаем вывод, что

Тело, погруженное (полностью или частично) в жидкость, испытывает со стороны жидкости суммарное давление, направленное снизу вверх и равное весу жидкости в объеме погруженной части тела.

Для однородного тела плавающего на поверхности справедливо соотношение

где: V — объем плавающего тела;
ρ_m — плотность тела.

Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь гидравлической сущности этой теории.

Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние называется устойчивостью. Вес жидкости, взятой в объеме погруженной части судна называютводоизмещением, а точку приложения равнодействующей давления (т.е. центр давления) — центром водоизмещения. При нормальном положении судна центр тяжести С и центр водоизмещения d лежат на одной вертикальной прямой O’-O», представляющей ось симметрии судна и называемой осью плавания (рис.2.5).

Пусть под влиянием внешних сил судно наклонилось на некоторый угол α, часть судна KLM вышла из жидкости, а часть K’L’M’, наоборот, погрузилось в нее. При этом получили новое положении центра водоизмещения d’. Приложим к точке d’ подъемную силу R и линию ее действия продолжим до пересечения с осью симметрии O’-O». Полученная точка m называется метацентром, а отрезок mC = h называетсяметацентрической высотой. Будем считать h положительным, если точка m лежит выше точки C, и отрицательным — в противном случае.

Теперь рассмотрим условия равновесия судна:

1) если h > 0, то судно возвращается в первоначальное положение;
2) если h = 0, то это случай безразличного равновесия;
3) если h

Следовательно, чем ниже расположен центр тяжести и, чем больше метацентрическая высота, тем больше будет остойчивость судна.

Как уже отмечалось выше, поверхность, во всех точках которой давление одинаково, называетсяповерхностью уровня или поверхностью равного давления. При неравномерном или непрямолинейном движении на частицы жидкости кроме силы тяжести действуют еще и силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.

Рассмотрим два примера такого относительного покоя.

В первом примере определим поверхности уровня в жидкости, находящейся в цистерне, в то время как цистерна движется по горизонтальному пути с постоянным ускорением a (рис.2.6).

К каждой частице жидкости массы m должны быть в этом случае приложены ее вес G = mg и сила инерцииP_u, равная по величине ma. Равнодействующая этих сил направлена к вертикали под углом α, тангенс которого равен

Так как свободная поверхность, как поверхность равного давления, должна быть нормальна к указанной равнодействующей, то она в данном случае представит собой уже не горизонтальную плоскость, а наклонную, составляющую угол α с горизонтом. Учитывая, что величина этого угла зависит только от ускорений, приходим к выводу, что положение свободной поверхности не будет зависеть от рода находящейся в цистерне жидкости. Любая другая поверхность уровня в жидкости также будет плоскостью, наклоненной к горизонту под углом α. Если бы движение цистерны было не равноускоренным, а равнозамедленным, направление ускорения изменилось бы на обратное, и наклон свободной поверхности обратился бы в другую сторону (см. рис.2.6, пунктир).

В качестве второго примера рассмотрим часто встречающийся в практике случай относительного покоя жидкости во вращающихся сосудах (например, в сепараторах и центрифугах, применяемых для разделения жидкостей). В этом случае (рис.2.7) на любую частицу жидкости при ее относительном равновесии действуют массовые силы: сила тяжести G = mg и центробежная сила P_u = mω 2 r, где r — расстояние частицы от оси вращения, а ω — угловая скорость вращения сосуда.

Поверхность жидкости также должна быть нормальна в каждой точке к равнодействующей этих сил R и представит собой параболоид вращения. Из чертежа находим

С другой стороны:

где z — координата рассматриваемой точки. Таким образом, получаем:

или после интегрирования

В точке пересечения кривой АОВ с осью вращения r = 0, z = h = C, поэтому окончательно будем иметь

т.е. кривая АОВ является параболой, а свободная поверхность жидкости параболоидом. Такую же форму имеют и другие поверхности уровня.

Для определения закона изменения давления во вращающейся жидкости в функции радиуса и высоты выделим вертикальный цилиндрический объем жидкости с основанием в виде элементарной горизонтальной площадки dS (точка М) на произвольном радиусе r и высоте z и запишем условие его равновесия в вертикальном направлении. С учетом уравнения (2.11) будем иметь

После сокращений получим

Это значит, что давление возрастает пропорционально радиусу r и уменьшается пропорционально высоте z.

Содержание

Основное дифференциальное уравнение гидростатики
Страницы работы
Содержание работы
Основное дифференциальное уравнение гидростатики
Основы гидравлики
Основные физические свойства жидкости.
Гидростатика
Основное уравнение гидростатики
Вакуум. Закон Паскаля.
🔍 Видео

Видео:Уравнение Бернулли гидравликаСкачать

Основное дифференциальное уравнение гидростатики

Страницы работы

Содержание работы

Видео:Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать

Основное дифференциальное уравнение гидростатики

Рассмотрим внутри покоящейся жидкости параллелепипед с ребрами (рис. 2.3), расположенными параллельно координатным осям О_x, O_y, O_z и равными соответственно dx, dy, dz. Принимая во внимание, что уравнения моментов не имеют смысла, рассмотрим уравнение равновесия сил в проекциях на координатные оси.

å Х = 0; å Y = 0; å Z = 0. (2.12)

Для оси О_х имеем

dP — dP₁ + dFcosa = 0, (2.13)

где dP = pdydz и dP₁ = p ¢ dydz;

P₁ и P ¢ — средние гидростатические давления соответственно на площадки АВСДА и А ¢ В ¢ С ¢ Д ¢ А ¢ .

Принимая во внимание, что гидростатическое давление является функцией координат, среднее гидростатическое давление на площадке А ¢ В ¢ С ¢ Д ¢ А ¢ будет равно

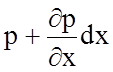
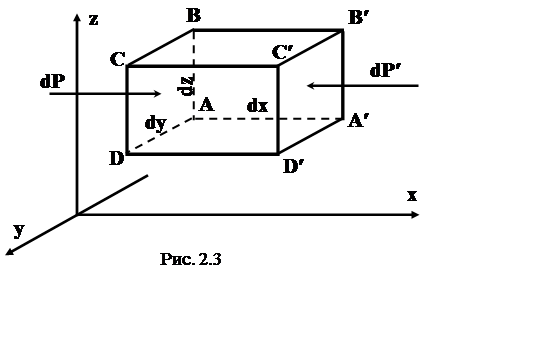p ¢ = . (2.14)

Какие параметры жидкости связывает основное дифференциальное уравнение гидростатики

Тогда, силу dP₁ можно определить, как

. (2.15)

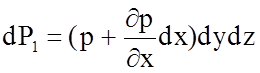
Объемная сила для массы dm, заключенной в объеме параллелепипеда, определится как

dF = dmjcosa = dmX = rdxdydzX. (2.16)

Подставляя значения слагаемых, получаем:

pdydz- + rXdxdydz = 0. (2.17)

Проводя преобразования (раскрывая скобки и сокращая на dxdydz ) получаем

. (2.18)

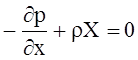
Аналогично получаются и уравнения проекций сил на оси Oy и Ox.

Тогда, систему уравнений описывающих условия равновесия жидкости (уравнение Эйлера) можно записать в виде

. (2.19)

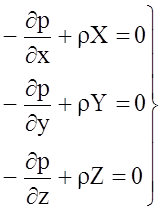
Запишем уравнение Эйлера в виде

. (2.20)

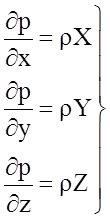
Умножая каждое из записанных уравнений на dx,dy и dz соответственно, и проводя сложение правых и левых частей уравнений, получим

. (2.21)

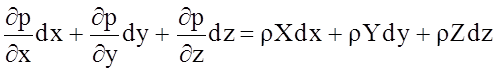
Принимая во внимание, что левая часть записанного уравнения представляет собой полный дифференциал dp функции p = p(x, y, z), имеем

dp = r (Xdx + Ydy + Zdz). (2.22)

Данное уравнение называется основным дифференциальным уравнением гидростатики.

Логично предположить, что правая часть уравнения представляет также полный дифференциал некоторой функции

Xdx + Ydy +Zdz = dU. (2.23)

Следовательно, X = ¶U/¶x; Y = ¶U/¶y; Z = ¶U/¶z.

Величины x, y, z представляют собой проекции ускорения объемной силы, которые можно рассматривать как проекций самой объемной силы, отнесенной к единице массы данной жидкости.

; (2.24)

; (2.25)

. (2.26)

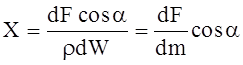
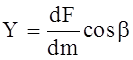
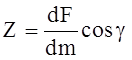
Функция U (x, y, z) является потенциалом сил или так называемой “силовой функцией”.

Таким образом, равновесие жидкости возможно, если объемные силы имеют потенциал.

Для поверхностей уровня наблюдается равенство давлений во всех точках — p = const и dp = 0.

Тогда, основное уравнение гидродинамики запишется в виде

Xdx + Ydy + Zdz = 0. (2.27)

Основные свойства поверхностей уровня:

1. Две поверхности уровня не пересекаются между собой.

2. Внешние объемные силы направлены нормально к поверхности уровня.

Видео:Закон БернуллиСкачать

Основы гидравлики

Учебные вопросы:

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Основные физические свойства жидкости.

В отличие от твердого тела жидкость характеризуется малым сцеплением между частицами, вследствие чего она обладает текучестью и принимает форму сосуда, в который ее помещают.

Жидкости подразделяют на два вида:

Капельные жидкости обладают большим сопротивлением сжатию (практически несжимаемы) и малым сопротивлением касательным и растягивающим усилиям (из-за незначительного сцепления частиц и малых сил трения между частицами).

К капельным жидкостям относятся вода, бензин, керосин, нефть, ртуть и другие

Газообразные жидкости характеризуются почти полным отсутствием сопротивления сжатию.К газообразным жидкостям относятся все газы.

К основным физическим свойствам жидкости относятся:

Плотность — это отношение массы к объему, занимаемому этой массой. Плотность измеряют в системе СИ в килограммах на кубический метр (кг/м3). Плотность воды составляет 1000 кг/м3.

Используются также укрупненные показатели: – килопаскаль — 1 кПа= 103 Па; – мегапаскаль — 1 МПа = 106 Па.

Сжимаемость жидкости — это ее свойство изменять объем при изменении давления. Это свойство характеризуется коэффициентом объемного сжатия или сжимаемости, выражающим относительное уменьшение объема жидкости при увеличении давления на единицу площади. Для расчетов в области строительной гидравлики воду считают несжимаемой. В связи с этим при решении практических задач сжимаемостью жидкости обычно пренебрегают.

Величина, обратная коэффициенту объемного сжатия, называется модулем упругости. Модуль упругости измеряется в паскалях

Температурное расширение жидкости при ее нагревании характеризуется коэффициентом температурного расширения, который показывает относительное увеличение объема жидкости при изменении температуры на 1 С.

В отличие от других тел объем воды при ее нагревании от 0 до 4 °С уменьшается. При 4 °С вода имеет наибольшую плотность и наибольший удельный вес; при дальнейшем нагревании ее объем увеличивается. Однако в расчетах многих сооружений при незначительных изменениях температуры воды и давления изменением этого коэффициента можно пренебречь.

Вязкость жидкости — ее свойство оказывать сопротивление относительному движению (сдвигу) частиц жидкости. Силы, возникающие в результате скольжения слоев жидкости, называют силами внутреннего трения, или силами вязкости.

Силы вязкости проявляются при движении реальной жидкости. Если жидкость находится в покое, то вязкость ее может быть принята равной нулю. С увеличением температуры вязкость жидкости быстро уменьшается; остается почти постоянной при изменении давления.

Гидростатика

В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением.

Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна.

Гидростатическое давление обладает свойствами

Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости.
Свойство 2. Гидростатическое давление неизменно во всех направлениях.
Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве.

Основное уравнение гидростатики

Рассмотрим распространенный случай равновесия жидкости, когда на нее действует только одна массовая сила – сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке рассматриваемого объема жидкости. Это уравнение называется основным уравнением гидростатики.

Пусть жидкость содержится в сосуде (рис.8 ) и на ее свободную поверхность действует давление P0 . Найдем гидростатическое давление P в произвольно взятой точке М, расположенной на глубине h. Выделим около точки М элементарную горизонтальную площадку dS и построим на ней вертикальный цилиндрический объем жидкости высотой h. Рассмотрим условие равновесия указанного объема жидкости, выделенного из общей массы жидкости. Давление жидкости на нижнее основание цилиндра теперь будет внешним и направлено по нормали внутрь объема, т.е. вверх.

Запишем сумму сил, действующих на рассматриваемый объем в проекции на вертикальную ось:

Полученное уравнение называют основным уравнением гидростатики. По нему можно посчитать давление в любой точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления P0 на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости.

Пьезометрический и гидростатический напоры

Рассмотрим закрытый сосуд с жидкостью, к которому в точках А и В на произвольной глубине присоединены пьезометры I и II (рис. 9).

Давление на свободной поверхности в сосуде больше атмосферного. Трубка I сверху открыта и давление на свободной поверхности в ней равно атмосферному. Трубка II сверху запаяна, из нее удален воздух, т.е. давление в ней равно нулю.

Для определения вертикальных координат точек А и В проведем на произвольной высоте горизонтальную плоскость 0-0. Эта плоскость называется плоскостью сравнения. Вертикальное расстояние от плоскости сравнения до рассматриваемой точки называется геометрической высотой точки по отношению к плоскости сравнения и обозначается буквой. За плоскость сравнения может быть принят уровень земли, пола.

Так как давление в сосуде на свободной поверхности жидкости больше атмосферного, то в пьезометрических трубках I и II жидкость поднимется на большую высоту, чем уровень жидкости в сосуде. Обозначим высоту поднятия жидкости в открытом пьезометре через – пьезометрическая высота, а высоту поднятия жидкости в закрытом пьезометре через – приведенная высота.

Пьезометрическая высота – мера манометрического давления в точке А. Приведенная высота – мера абсолютного давления в точке В. Разность высот , равна высоте столба жидкости, соответствующей атмосферному давлению т.е. 10 м.в.ст.

Сумма геометрической высоты и пьезометрической для любой точки жидкости будет величиной постоянной и называется пьезометрическим напором:

Подставив это выражение в формулу (1) получим:

это сумма приведенной высоты и геометрической высоты положения, называемая гидростатическим напором Hs.

В уравнении (5) Hs=const для любой точки жидкости, а не зависит от положения точки. Значит:

Поэтому, сколько бы мы пьезометров не подключили, во всех пьезометрах жидкость установится на одном уровне: плоскость, соответствующая уровню П–П, называется пьезометрической плоскостью, а уровню Н–Н – напорной плоскостью.

Пьезометрический напор является мерой удельной потенциальной энергии жидкости. Предположим, что вес частицы жидкости в точке А. равен G. о отношении к плоскости сравнения О – О запас потенциальной энергии положения равен G*z, где -Z высота от плоскости О – О до точки А.

Под действием избыточного гидростатического давления Pm частица, находящаяся на глубине h , может подняться на высоту hp, то есть она обладает потенциальной энергией давления равной G*hp. Полная потенциальная энергия частицы жидкости весом G равна G*z+G*hp.

Удельная потенциальная энергия, т.е. энергия приходящаяся на единицу веса частицы будет соответственно равна:

Аналогично, гидростатический напор Hs является также мерой удельной потенциальной энергии жидкости, но большей по сравнению Hp на величину удельной потенциальной энергии атмосферного давления.

Вакуум. Закон Паскаля.

Вакуум — пространство, свободное от вещества. В технике и прикладной физике под вакуумом понимают среду, содержащую газ при давлении значительно ниже атмосферного. Вакуум характеризуется соотношением между длиной свободного падения молекул газа λ и характерным размером среды d. Под d может приниматься расстояние между стенками вакуумной камеры, диаметр вакуумного трубопровода и т. д. В зависимости от величины соотношения λ/d различают низкий, средний и высокий вакуум.

Насос для демонстрации вакуума

Законом Паскаля в гидростатике называется следующее утверждение,сформулированное французским учёным Блезом Паскалем: давление, производимое на жидкость или газ, передается в любую точку без изменений во всех направлениях.

На основе закона Паскаля работают различные гидравлические устройства: тормозные системы, гидравлические процессы и др.

В законе Паскаля речь идет не о давлениях в разных точках гидравлической системы, а о возмущениях давления в разных точках, поэтому закон справедлив и для жидкости в поле силы тяжести.

В случае движущейся несжимаемой жидкости можно условно говорить о справедливости закона Паскаля, ибо добавление произвольной постоянной величины к давлению не меняет вида уравнения движения жидкости, однако в этом случае термин закон Паскаля обычно не применяется. Для сжимаемых жидкостей (газов) закон Паскаля, вообще говоря, несправедлив.

Виды движения жидкости

Виды движения жидкости бывают:

Неустановившимся – называют движение жидкости, все или некоторые характеристики которого изменяются во времени, т. е. давление и скорость зависят как от координат , так и от времени

Примерами неустановившегося движения являются опорожнение резервуаров, водохранилищ, движение воды в реках при переменном уровне (при паводках, сбросах воды через плотину) и т. д.

сброс воды через плотину

Установившимся – наз. движение жидкости неизменное во времени, при котором давление и скорость являются функциями только координат, но не зависит от времени. u = f1(x, y, z); p = f2(x, y, z).

Установившееся движение подразделяется на:

Равномерное движение характеризуется постоянством параметров по длине потока. Примерами такого движения являются движения в трубах постоянного сечения и в каналах правильной формы. Поле линий тока равномерного движения – семейство параллельных прямых.

При неравномерном движении скорость, глубина, площади сечений потока изменяются по его длине. Из неравномерных движений можно выделить так называемое плавно изменяющееся движение, которое характеризуется малой кривизной линий тока и малым углом расхождения линий тока .

В зависимости от причин, вызывающих движение, и условий, в которых оно происходит, различают:

напорное движение
безнапорное движение

Напорное движение происходит в потоке, со всех сторон ограниченном твердыми стенками. Давление во всех точках потока отлично от атмосферного и может быть как больше, так и меньше последнего. Движение происходит под действием разности давлений по длине потока, которая может быть создана водонапорной башней, питающим баком, насосной установкой.

Безнапорное движение происходит под действием силы тяжести при наличии свободной поверхности жидкости. Примерами безнапорного движения является движение в реках, каналах и трубах, когда сечение последних не полностью заполнено жидкостью.

Гидродинамика

Предметом изучения гидродинамики является движущаяся жидкость. Как было указано ранее, все без исключения физические и химические процессы, которые составляют основу промышленных технологических процессов, происходят в динамических условиях, в условиях движения текучих сред.

При движении жидкостей под воздействием внешних сил в потоках прежде всего формируются поля скоростей микро- и макрочастиц, которые определяют формирование температурных и полей концентраций веществ, что в конечном итоге обусловливает скорость протекания процессов.

На движущуюся жидкость, кроме сил, которые действовали на покоящуюся жидкость (поверхностные силы гидростатического давления и массовые силы: силы тяжести и внешние силы инерции), действуют дополнительные силы инерции и силы трения. В отличие от гидростатического давления, величина которого не зависит от ориентации поверхности, на которое оно действует, возникающее при движении гидродинамическое давление благодаря развитию напряжениям сдвига (касательным силам), различно в направлении осей X, Y и Z.

Наличие сил внутреннего трения между движущимися частицами жидкости (в соответствии с законом внутреннего трения Ньютона) является первопричиной различия скоростей движения в различных точках по поперечному сечению канала. Характер этого различия, который обусловливается характером связи между давлением и скоростью движения частиц в любой точке потока. Это и является основной задачей теории гидродинамики.

Уравнение неразрывности потока.

Уравнение неразрывности потока отражает закон сохранения массы: количество втекающей жидкости равно количеству вытекающей. Например, на рис. 15 расходы во входном и выходном сечениях напорной трубы равны: q1 = q2.

Схема к уравнению неразрывности потока.

С учётом, что q = Vw, получим уравнение неразрывности потока:

Если отсюда выразим скорость для выходного сечения:

то легко заметить, что она увеличивается обратно пропорционально площади живого сечения потока. Такая обратная зависимость между скоростью и площадью является важным следствием уравнения неразрывности и применяется в технике, например, при тушении пожара для получения сильной и дальнобойной струи воды.

Ламинарный и турбулентный режим движения жидкости.

Наблюдения показывают, что в природе существует два разных движения жидкости:

слоистое упорядоченное течение – ламинарное движение, при котором слои жидкости скользят друг друга, не смешиваясь между собой;
турбулентное неурегулированное течение, при котором частицы жидкости движутся по сложным траекториям, и при этом происходит перемешивание жидкости.

От чего зависит характер движения жидкости, установил Рейнольдс в 1883 году путем. Эксперименты показали, что переход от ламинарного к турбулентному движению происходит при определенной скорости (критическая скорость), которая для труб различных диаметров неодинакова: при увеличении диаметра она увеличивается, критическая скорость так же увеличивается при увеличении вязкости жидкости. Рейнольдс вывел общие условия существования ламинарного и турбулентных режимов движения жидкости. По Рейнольдсу режима движения жидкости зависят от безразмерного числа, которое учитывает основные, определяющие это движение: среднюю скорость, диаметр трубы, плотность жидкости и ее абсолютную вязкость.

Это число называется числом Рейнольдса:

Число Рейнольдса, при котором происходит переход от одного режима движения жидкости в другой режим, называется критическим .

При числе Рейнольдса наблюдается ламинарный режим движения, при числе Рейнольдса – турбулентный режим движения жидкости. Чаще критическое значение числа принимают равным это значение соответствует переходу движения жидкости от турбулентного режима к ламинарного.

При переходе от ламинарного режима движения жидкости к турбулентному критическое значение имеет большее значение. Критическое значение числа Рейнольдса увеличивается в трубах, сужаются, и уменьшается в тех, что расширяются. Это объясняется тем, что при сужении поперечного сечения скорость движения частиц увеличивается, поэтому тенденция к поперечного перемещения уменьшается.

Уравнение Бернулли.

Закон (уравнение) Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

p — плотность жидкости,

v— скорость потока,

h— высота, на которой находится рассматриваемый элемент жидкости,

p— давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,

g— ускорение свободного падения.

Константа в правой части часто называется полным давлением и зависит, в общем случае, от линии тока.

Размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости. Первое и второе слагаемое в интеграле Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. Следует обратить внимание на то, что третье слагаемое по своему происхождению является работой сил давления и не представляет собой запаса какого-либо специального вида энергии .

Соотношение, близкое к приведенному выше, было получено в 1739 г. Даниилом Бернулли, с именем которого обычно связывают интеграл Бернулли. В современном виде интеграл был получен Иоганном Бернулли около 1740 года.

Bernoulli Johann 1667-1748

СВОЙСТВА ГАЗОВ И ЖИДКОСТЕЙ

Список литературы:

1. В.П. Гусев «Основы гидравлики», Томск, 2009 г.

2. Бретшнайдер С. «Свойства газов и жидкостей», Москва