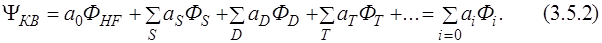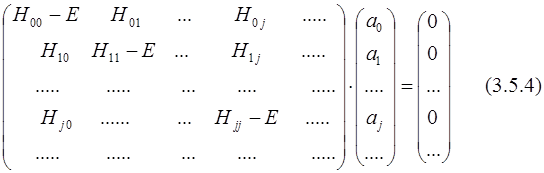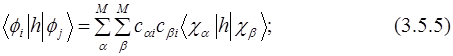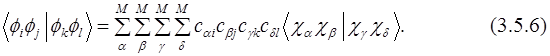Какие параметры молекулы необходимо задать при решении электронного уравнения шредингера

Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Молекулярное уравнение Шредингера

Квантово-механическое рассмотрение атомных и молекулярных систем зависит от того, являются ли такие системы свободными или имеется внешнее поле, действующее на частицы составляющие атом или молекулу. Более просты, вообще говоря, построения в тех случаях, когда эти системы свободны, а потому с них мы и начнем изложение квантовой механики молекул. При этом до тех пор, пока не будет особой необходимости, различать атомы и молекулы не будем. Кроме того, будем использовать систему атомных единиц.

а. Стационарное уравнение Шредингера.

Для свободных систем можно перейти от исходного временного к стационарному уравнению Шредингера, которое записывается в обычном виде:

где отдельные слагаемые имеют смысл

— кинетической энергии ядер:

— кинетической энергии электронов:

— потенциала взаимодействия электронов между собой, представляемого, например, кулоновским взаимодействием:

где Гу — расстояние между электронами с индексами / иу ;

— потенциала взаимодействия электронов с ядрами:

где Z_a — заряд ядра a, R_ia — расстояние от электрона i до ядра а;

— потенциала взаимодействия ядер между собой:

где Л_ар- расстояние между ядрами с индексами а и р. Конечно, в более общем подходе, когда рассматриваются и другие взаимодействия в системе, например взаимодействие каждого электрона с магнитным полем остальных электронов, приведенных выражений для потенциалов уже будет недостаточно. Характерно, однако, что при этом будут выполняться следующие соотношения:

где g(i,j) = g(j, /) — некоторая функция, зависящая от переменных /- иу’-го электронов, симметричная относительно перестановки этих переменных и по своему аналитическому виду одна и та же для любой пары электронов;

где V_v(a_v,/) — одна и та же функция для-каждой пары, состоящей из ядра вида v с индексом a_v (например, любого из протонов в молекуле углеводорода) и электрона с индексом /; число s указывает, сколько различных видов ядер встречается в молекуле;

Формулами (4) мы пока пользоваться не будем, коль скоро сущности последующих рассуждений это не меняет.

Видео:Урок 455. Уравнение ШрёдингераСкачать

Лекция №1. Квантов0механическ0е обоснование теории строения молекул и химической связи. Строение атома (стр. 4 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9

Из различных методов определения СЭ наиболее прямой и точный — измерение минимальной энергии фотоотрыва электрона от отрицательного иона.

Для большинства атомов присоединение электрона — экзотермический процесс. Наиболее высоким по абсолютной величине сродством к электрону обладают атомы галогенов в последовательности Cl > F > Вг > I. Энергии ионизации и сродство к электрону молекул определяют также, как это сделано для атома.

ТЕОРЕТИЧЕСКИЕ МЕТОДЫ, ПРИМЕНЯЕМЫЕ ПРИ ИЗУЧЕНИИ СТРОЕНИЯ МОЛЕКУЛ И ХИМИЧЕСКОЙ СВЯЗИ

Видео:Лекции 5-6. Уравнение Шредингера и его приближенные решения. Межатомные.Скачать

1. Молекула. Потенциальная поверхность. Равновесная конфигурация

2. Теория химической связи и её задачи.

3. Вариационный метод решения уравнения Шрёдингера.

§1. Молекула. Потенциальная поверхность. Равновесная конфгурация.

В химии молекулой называют наименьшую частицу данного вещества, обладающую его химическими свойствами, способную к самостоятельному существованию. Если отвлечься от поступательного движения молекулы как целого, то в ее энергию вносят вклад три вида движения: 1) движение электронов в поле ядер, 2) колебание ядер около положения равновесия и вращение молекулы вокруг оси, проходящей через центр масс, причем Еэл >> Екол >>Евр.

Хотя эти движения взаимосвязаны, можно приближенно рассматривать их как независимые и считать энергию молекулы равной сумме электронной, колебательной и вращательной энергий:

Е = Еэл + Екол +Евр. (6.1)

Волновая функция молекулы в этом приближении равна произведению функций, описывающих указанные три вида движения:

(6.2)

Остановимся на наиболее важной составляющей энергии молекулы — электронной энергии. Так как скорость тяжелых ядер во много раз меньше скорости легких электронов, приближенно можно рассматривать движение электронов в молекуле в каждый данный момент, считая ядра неподвижными (приближение Борна — Оппенгеймера). Выбранному фиксированному положению ядер R отвечает определенная энергия электронов , включающая их кинетическую энергию, энергию взаимодействия электронов друг с другом и энергию взаимодействия электронов с ядрами.

Условимся включать сюда также энергию отталкивания ядер . Тогда название «электронная» для указывает, что учитывается движение только электронов, но не ядер, а фиксированное расстояние между ядрами R рассматривается как параметр. Индекс «эл» при этом можно опустить (Eкол и Евр здесь не рассматриваются). Если расстояние между ядрами R изменится, изменится поле ядер, в котором движутся электроны, изменится и электронная энергия системы . В этом смысле электронная энергия есть функция межъядерного расстояния и по отношению к движению ядер играет роль потенциальной энергии. Вид функции для двухатомной молекулы АВ изображает кривая о рис. 5.1., называемая потенциальной кривой. Когда атомы А и В удалены на бесконечное расстояние, электронная энергия равна сумме электронных энергий невзаимодействующих атомов А и В в основном состоянии: .

При сближении ядер электронная энергия понижается (сила притяжения электронов к ядрам преобладает над силами отталкивания между ядрами и между электронами). Затем потенциальная кривая проходит через минимум при R = rе и при дальнейшем сближении ядер возрастает, стремясь к бесконечности при R →0 (преобладает сила отталкивания). Межъядерное расстояние R=re, отвечающее минимуму потенциальной кривой, называется равновесным. При R=re равнодействующая всех сил притяжения и отталкивания равна нулю, молекула находится в устойчивом состоянии. Этому состоянию отвечает строго определенное значение электронной энергии молекулы. За нуль отсчета энергии можно принять, как и для атома, энергию невзаимодействующих электронов и ядер. Разность между суммой энергий невзаимодействующих атомов и Eэл. мол называют энергией химической связи или энергией диссоциации молекулы, отсчитанной от минимума потенциальной кривой, и обозначают De (глубина «потенциальной ямы»):

Данная потенциальная кривая соответствует классическим представлениям. Однако в нее надо внести поправки, так как равновесное состояние неосуществимо с точки зрения квантовой механики: в этом состоянии ядра неподвижны, значит, одновременно точно определены координата (R = rе) и импульс (р = 0), что противоречит соотношению неопределенностей Гейзенберга. Параметры rе и De (рис. 6.1) относятся таким образом к гипотетическому равновесному состоянию. В действительности даже и при 0К ядра не зафиксированы при R — rе, а совершают колебания около положения равновесия. Реальная энергия молекулы при этом выше, чем предполагалась, на величину энергии «нулевых колебаний» (рис.6.1). При нулевых колебаниях расстояние R между ядрами изменяется, в результате чего нулевой колебательный уровень характеризуется некоторым усредненным значением r0, которое из-за асимметрии потенциальной кривой незначительно, отличается от гипотетического равновесного расстояния rе=0,751·10-10 м и 0,741·10-10 м соответственно для Н2).

Определяемая на опыте энергия диссоциации молекулы D0 отсчитывается не от минимума потенциальной кривой как De, а от уровня нулевых колебаний (рис.и связана с De соотношением

(6.4)

Энергия диссоциации D0, служит мерой прочности химической связи и определяется как изменение энергии в процессе — АВ = А + В при 0 К в идеально-газовом состоянии. Если специальных указаний нет, то понимается, что как молекула АВ, так и атомы А и В находятся в основном электронном состоянии. Это определение сохраняет силу и для многоатомных молекул. Например, для молекулы AmBn энергией диссоциации будет изменение энергии в процессе AmBn = mA + nB.

Потенциальная поверхность. Равновесная конфигурация. При описании потенциальной кривой вместо Eэл. мол обычно используют символ E(R) или Е. Для многоатомной молекулы Е является функцией уже не одной, а нескольких пространственных координат Rij. Например, потенциальная энергия молекулы ABC является функцией трех независимых координат — R1(A — В), R2(B — С) и угла о(АВС) или расстояний R1(A — В), R2(B — С) и R3(А — С).

Для линейной молекулы с фиксированным углом α- 180° эта функция изобразится поверхностью в трехмерном пространстве (потенциальная поверхность) Устойчивому состоянию молекулы отвечает минимальное значение ее энергии E(АВС) и определенное относительное расположение ядер в пространстве, называемое равновесной конфигурацией молекулы с параметрами rе(А — В) и rе(В — С). Глубина потенциальной ямы определяет энергию химической связи De и по формуле (5.4) энергию диссоциации молекулы D0.

Для более сложной молекулы, чем линейная ABC, равновесная конфигурация и энергия равновесного состояния определяются положением минимума на потенциальной поверхности в многомерном пространстве. Если потенциальная поверхность имеет два (или более) минимума, для молекулы возможны два изомера или более, отличающиеся параметрами равновесной конфигурации и энергией. Если минимума на потенциальной поверхности нет, данная система нестабильна, при любом расположении ядер она распадается на невзаимодействующие атомы.

Так же как и атом, молекулу можно перевести в возбужденные электронные состояния (энергия возбуждения Те), каждому из которых отвечает своя потенциальная поверхность или кривая (кривая б на рис. 6.1).

Рассмотрев потенциальную кривую (поверхность), можно дать еще одно определение молекулы молекула — физически устойчивая система, состоящая из двух (или более) ядер и определенного числа электронов, состояние которой описывается потенциальной кривой (поверхностью) с минимумом.

Говоря о физической устойчивости, понимают, что соединение атомов в молекулу сопровождается понижением энергии системы. Данным здесь определением охватываются кроме обычных молекул (Н2, СН4 и др.) также радикалы (СН, ОН, СН3 и др.) и молекулярные ионы (Н+, O2— и др.). Этому отвечает одинаковый подход теории строения к изучению перечисленных типов частиц. В тех случаях, когда молекулы одноатомны (благородные газы, пары металлов), сохраняет силу аналогичное определение для атома.

Равновесная конфигурация предполагает жесткую фиксацию всех межъядерных расстояний в молекуле. Однако реальная молекула не является жесткой системой. Вместе с тем у огромного большинства молекул амплитуды колебаний ядер весьма малы по сравнению с межъядерными расстояниями и можно, пренебрегая колебаниями, рассматривать молекулы как жесткие системы («квазижесткие» или «квазитвердые» молекулы).

Равновесные конфигурации молекул принято относить к тем или иным точечным группам симметрии.

Двухатомные молекулы подразделяются на молекулы с одинаковыми ядрами, или гомонуклеарные (например, Н2), и с неодинаковыми ядрами, или гетеронуклеарные (например, HCI). Свойства симметрии их различны.

Симметрия равновесной конфигурации определяет и симметрию электронного облака молекулы. В связи с этим гомонуклеарные и гетеронуклеарные молекулы различаются по электрическим и оптическим свойствам, таким, как дипольный момент, поляризуемость и магнитная восприимчивость, правила отбора в спектрах. То же относится и к многоатомным молекулам, различающимся по симметрии, как, например, СН4 и СН3С1.

Рассмотренные молекулярные параметры: энергия диссоциации, межъядерные расстояния, равновесная конфигурация важны для химии не только как индивидуальные характеристики молекул. По ним можно рассчитать термодинамические свойства веществ и константы равновесия химических реакций.

§2. Теория химической связи и ее задачи. Уравнение Шредингера для молекул

Взаимодействие атомов, приводящее к образованию молекул простых и сложных веществ, а также кристаллов, называют химической связью. Взаимодействие атомов многообразно, поэтому многообразны и химические связи, которые часто сводят к нескольким основным типам: ковалентной, ионной, донорно-акцепторной, водородной связи и др. Однако все эти взаимодействия можно описать с позиций единой теории химической связи.

1) Эта теория призвана объяснить, какие силы действуют между атомами, как атомы объединяются в молекулы, что обеспечивает устойчивость образовавшейся сложной частицы (то же относится к кристаллам, жидкостям и другим телам).

2) Теория должна объяснить опытные факты, лежащие в основе классического понятия валентности, и наряду с этим существование и устойчивость многочисленных соединений, не укладывающихся в привычные рамки классических структурно-химических представлений.

3) Теория должна разработать единые методы расчета молекулярных параметров, интерпретировать молекулярные спектры.

4) Наконец, теория должна сделать возможным априорный расчет скорости химического процесса, зависимости ее от строения молекул реагирующих веществ.

Современная теория химической связи, теория строения молекул и кристаллов базируется на квантовой механике: молекулы, как и атомы, построены из ядер и электронов, и теория химической связи должна учитывать корпускулярно-волновой дуализм микрочастиц. До применения методов квантовой механики к химии не удавалось создать непротиворечивую теорию химической связи.

Её фундамент был заложен в 1927 г. Гейтлером и Лондоном. Выполнив на основе квантовой механики расчет свойств молекулы водорода, они показали, что природа химической связи электрическая, никаких особых сил химического взаимодействия не существует. Действующие в молекуле между ядрами и электронами гравитационные и магнитные силы пренебрежимо малы по сравнению с электрическими силами.

Квантовомеханический подход к исследованию строения атома и молекулы один и тот же: нужно составить и решить уравнение Шредингера для системы из электронов и ядер и дать физическую интерпретацию полученным решениям. Составляя уравнение Шрёдингера для электронной энергии молекулы в приближении Борна — Оппенгеймера, считают ядра неподвижными.

Следовательно, электронная энергия для молекулы не зависит от координат ядер, а только от фиксированного расстояния R между ними (рис. 6.2). Во внимание принимаются лишь изменения координат электронов. Простейшая из молекул молекулярный ион содержит один электрон и два ядра. Для одного электрона в поле двух ядер (ион ) уравнение Шредингера имеет вид

. (6.5)

Для молекулярного иона потенциальная энергия

(6.6)

включает притяжение электрона 1 к ядрам А и В (первые два члена) и отталкивание ядер (ядра А и В у совершенно одинаковы — это протоны). Для иона с учетом (6.6) уравнение Шредингера принимает вид

, (6.7)

где Ψ — одноэлектронная волновая функция (собственная функция Шредингера для системы с одним электроном). Индексы «эл. мол.» при E и Ψ — опущены для упрощения записи.

Состояние молекулы Н2 описывается уже двухэлектронной функцией Ψ, зависящей от координат двух электронов (см. рис. 6.2).

Многоэлектронными будут и волновые функции более сложных молекул. Уравнение Шредингера для молекулы Н2 имеет вид

(6.8)

Индексы 1 и 2 при операторах Лапласа указывают, что волновая функция молекулы дифференцируется по координатам первого () и второго () электронов. Усложнится и выражение для потенциальной энергии:

(6.9)

В (6.9) первые четыре члена обозначают потенциальную энергию притяжения электронов 1 и 2 к ядрам А и В соответственно, пятый член — потенциальную энергию взаимного отталкивания электронов 1 и 2, последний член — энергию отталкивания ядер. Аналогично записывается уравнение Шредингера и для многоатомных молекул. В уравнениях (6.7) и (6.8) используется координатная молекулярная функция Ψ. Полная волновая функция молекулы Фмол, учитывающая и спин, должна удовлетворять принципу Паули антисимметрии волновых функций и строится в виде определителя.

Для молекулы, так же как и для атома, точное решение уравнения Шредингера возможно лишь для системы, содержащей один электрон — для молекулярного иона типа . Уже для молекулы Н2 в выражении (6.9) появляется член (энергия электронного отталкивания), зависящий от координат двух электронов, и точное решение невозможно. Однако принципиальный ответ о природе химической связи можно получить и при помощи приближенных методов решения волнового уравнения.

§3. Вариационный метод решения уравнения Шрёдингера

Одним из широко применяемых при рассмотрении теории химической связи приближенных методов решения уравнения Шредингера является вариационный метод. Здесь коротко излагается его сущность.

Уравнение Шредингера (1.1) может быть представлено в так называемой операторной форме. Для этого разделим все члены уравнения на и перегруппируем члены. Получим

.

Сумма двух действий, производимых над функцией Ψ в левой части, дифференцирование и умножение, может быть записана с помощью оператора ,

который называют оператором энергии, оператором Гамильтона или гамильтонианом. Уравнение приобретает лаконичную форму:

По такому же принципу строится оператор Гамильтона для многоатомных систем, например, для молекулы Н2

(6.11)

Умножим обе части уравнения Шредингера (6.10) на функцию Ψ*, комплексно сопряженную с волновой функцией

. (6.12)

Если Ψ — действительная функция, то Ψ*=-Ψ. (Левую сторону уравнения (6.12) нельзя записать аналогично правой в виде , так как в отличие от E — оператор, а не число). Возьмем интеграл от обеих частей (5.12) по всему пространству, причем Е как постоянную величину вынесем за знак интеграла:

.

. (6.13)

Если функция Ψ нормирована, знаменатель обращается в единицу и

. (6.14)

Если известно точное выражение для Ψ, то энергия системы может быть рассчитана по формулам (6.13) или (6.14). Однако, обычно не известны ни Ψ ни Е либо неизвестна Ψ. Тогда для отыскания Ψ и Е можно воспользоваться вариационным принципом: подставив в (6.13) или (6.14) вместо истинной функции приближенную к ней так называемую пробную функцию Ψпробн, получим отвечающее ей значение Е. Оно обязательно будет не ниже энергии основного состояния системы E0

. (6.15)

Видео:Елютин П. В. - Квантовая теория I - Свойства решений стационарного уравнения ШредингераСкачать

Решение уравнения Шрёдингера для молекулы водорода, для гомоядерных и гетероядерных двухатомных молекул. Молекулярные термы

Электронные состояния атомов нумеруют с помощью квантового числа L , задающего квадрат суммарного углового момента электронов. В отсутствии внешних полей все направления равноправны, и состояния с разными проекциями момента на ось z (напомним, что таких состояний ровно 2L+1) имеют одинаковую энергию. В результате энергетические уровни 2L+1-кратно вырождены. Обычно значения L задают буквами, как в атоме водорода, где состояния обозначаются как s, p, d… при значениях квантового числа l , описывающих угловой момент электрона, 0, 1, 2, . соответственно. Как принято в квантовой механике, для состояний многоэлектронных систем используются заглавные буквы: состояниям с L = 0, 1, 2. соответствуют символы S, P, D,…латинского алфавита.

Атом обладает очень высокой сферической симметрией и классификация состояний по угловому моменту – это классификация по типам симметрии относительно всевозможных поворотов. Кроме поворотов группа симметрии атома включает инверсию. При инверсии волновая функция может либо сохранять, либо менять знак, т.е. состояния обладают определенной четностью. Четность указывают не всегда, причем раньше её указывали нижними индексами g или u (от немецких слов gerade и ungerade), а потом стали использовать верхние индексы «o» (от английского слова odd) для указания только нечетных состояний. В верхнем левом углу символа состояния указывают спиновую мультиплетность – число 2S+1. Принято называть состояния с заданной мультиплетностью 2S+1 синглетными (S = 0, 2S+1 = 1), триплетными (S = 1, 2S+1 = 3), квинтетными (S = 1, 2S+1 = 3) и т.д. (при четном числе электронов в атоме и, следовательно, целом значении S ) и дублетными (S = 1/2, 2S+1 = 2), квартетными (S = 3/2, 2S+1 = 4), секстетными (S = 5/2, 2S+1 = 6). (при нечетном числе электронов). Состояние атома с данными L и S вырождено (2S+1)×(2L+1) раз.

Например, низшие по энергии состояния атома азота – это 4 S o , 2 D o , 2 P o , 4 P, 2 P, . Cимвол состояния 2 D o , например, произносится так: «нечетное дублетное D-состояние». Это состояние имеет кратность вырождения 2×(2×2+1) = 10 , а четное квартетное Р-состояние (4P) – 4×3 = 12.

При заметном спин-орбитальном взаимодействии имеет смысл лишь суммарный электронный момент J = L+S . Число J, нумерующее собственные значения квадрата суммарного момента указывают обычно справа внизу символа состояния. Такое состояние вырождено 2J+1 раз.Для тяжелых атомов иногда указывают только J (цифрой) и чётность состояния. Индексы i и r, используемые иногда в символах состояний, указывают на заполнение валентной оболочки больше, или меньше чем на половину. Одну и ту же конфигурацию, например, 1s 2 2s 2 2p 2 имеют принципиально разные электронные состояния 3 P₀, 3 P₁, 3 P₂, 1 D₂ , 1 S₀ (приведены в порядке возрастания энергии, определяемом иногда правилами Гунда) атома С. Электронные термы этих состояний составляют соответственно 0, 16.40, 43.40, 10192.63, 21648,01 см-1 (терм низшего по энергии, основного состояния по традиции принимается равным нулю). Напомним также, что задание волновой функции электронной конфигурацией имеет смысл лишь в контексте приближенных методов типа Хартри–Фока или функционала плотности.

Двухатомная молекула обладает довольно высокой симметрией. Два ядра лежат на оси z и задают аксиально-симметричный потенциал, в котором движутся электроны. Группа симметрии ядерной конфигурации включает операции поворотов вокруг осисимметрии С ∞ и отражения в любых плоскостях симметрии σv, содержащих эту ось. Такая группа симметрии – С ∞v – соответствует гетероядерным молекулам. В случае гомоядерных молекул имеется ещё центр инверсии i, а также другие элементы симметрии, вызванные наличием i: любые оси симметрии второго порядка, проходящие через центр и перпендикулярные оси z, а также плоскость симметрии σh , перпендикулярная оси z. Эти молекулыотносятся к группе симметрии D∞h. Осевая симметрия позволяет классифицировать электронные состояния с помощью оператора проекции суммарного электронного углового момента Lz . Собственные значения этого оператора задаются числами hLz (Lz =0, ±1, . ) и, с классической точки зрения, описывают вращение электронов вокруг оси z. Поскольку вращению по- и против часовой стрелки должна отвечать одинаковая энергия, энергии состояний с одинаковыми значениями Λ=|Lz| , но разными знаками Lz, должны совпадать, т.е. эти состояния двукратно вырождены (если не принимается во внимание спин-орбитальное взаимодействие). Электронные состояния двухатомных молекул классифицируются по значениям квантовых чисел Λ и чисел, описывающих квадрат спина (S) и проекцию спина на ось z (Σ). При этом используют буквенные обозначения, похожие на обозначения состояний с разным угловым моментом для атомов. Если описывают симметрию волновых функций одноэлектронных состояний (т.е. орбиталей) с Λ = 0, 1, 2, 3,…, используют буквы греческого алфавита : σ, π, δ, ϕ… Для многоэлектронных систем используются заглавные буквы: Σ, Π, Δ, Φ.

Примечание: Соответствие s – σ, p – π, d – δ, f – Φ очевидно, но далее символы следуют в соответствии с греческим алфавитом: при Λ = 4, например, орбитали имеют тип ψ, а многоэлектронные функции – Ψ. В случае Σ-состояний возможно различие в волновых функции относительно отражения в плоскости σv : волновые функции состояний типа Σ+ не изменяются, а в случае состояний Σ– меняют знак на противоположный (для орбиталей в трехмерном пространстве эту четность не указывают, так как нельзя построить ненулевую орбиталь σ–типа). При Λ > 0 операции отражения σv соответствует уже рассмотренное изменение направления вращения. Для гомоядерных систем надо еще указать, меняет или не меняет знак функция при инверсии. Нечетные и четные функции обозначают нижними правыми индексами u или g соответственно. В верхнем левом углу символа состояния указывают спиновую мультиплетность – число 2S+1. Основное, самое нижнее по энергии электронное состояние обозначается буквой Х, следующие по энергии – заглавными буквами латинского алфавита А, В, С…, если состояния имеют ту же мультиплетность 2S+1, что и основное, или малыми буквами a, b, c,…, если они отличаются по спину; иногда используют штрихи при буквенных символах. Отметим, что в этой номенклатуре есть и исторически сложившиеся исключения. Дело в том, что нумерация электронных состояний «по имени» складывалась в том порядке, в котором эти состояния открывались (чаще всего в этих случаях используются символы состояния со штрихами).

Вырождение состояний с разными проекциями спина происходит, лишь, если в молекуле отсутствует или очень мало спин-орбитальное взаимодействие. Если оно велико, (что типично для молекул с тяжелыми ядрами), то электронное состояние молекулы характеризуется не только числом Λ, но и числом Ω, равным модулю проекции суммарного электронного момента импульса на ось: Ω=|Lz+Σ|. Например, для состояния типа 2Π возможные значения Ω могут быть равны 3/2 (при Lz =1, Σ = +1/2, или при Lz = –1, Σ = –1/2) и 1/2 (при Lz =1, Σ = –1/2 или при Lz = –1, Σ = +1/2 ). Такие состояния обозначают дополнительным символом Ω в правом нижнем углу (или в скобках).

Среднее значение электронного гамильтониана в электронном состоянии Ψn – это электронная энергия En. Она то и играет роль потенциальной энергии при изучении движений ядер с помощью ядерного уравнения Шредингера. Для двухатомной молекулы это уравнение можно записать так: ( формула)

http://www.chem.msu.su/rus/teaching/kovba-pupyshev/kovba-pupyshev-spectra.pdf(стр.12 ) Здесь ψn,k – ядерная волновая функция, ε

n,k – энергетические уровни молекулы, а символы n и k использованы для указания состояний электронов (n) и состояний ядер (k).

Ядерное уравнение Шредингера описывает поведение двух ядер под действием потенциала En , зависящего лишь от взаимного расположения ядер в пространстве. Из курса физики известно, что подобные «задачи двух тел» можно решить, используя радиус-вектор центра масс и вектор относительного положения ядер: ( формула)

В этом случае ядерный гамильтониан оказывается суммой двух гамильтонианов, один из которых – кинетическая энергия центра масс, зависящая лишь от координат центра масс. Этот оператор описывает свободное движение центра масс молекулы (соответствующая волновая функция – это , где k – волновой вектор, показывающий направление импульса центра масс, а энергия поступательного движения центра масс равна (формула) . Второй гамильтониан зависит только от переменных

относительного движения R; информация о строении молекулы в основном содержится именно в этом гамильтониане. Поскольку переменные разделяются, функция стационарного состояний будет произведением волновых функций свободного движения центра масс и функции относительного движения частиц, зависящей лишь от R, так что, изучая переходы в молекуле, мы будем рассматривать только изменения этой функции. В классической модели это построение отвечает разбиению энергии молекулы на поступательную и внутреннюю.

После отделения переменных центра масс ядерное уравнение Шредингера (7.1) будет иметь вид: ( формула) (7.2),

где R = Ra– Rb, μ – приведенная масса : (формула). В сферических координатах (R,θ,ϕ) оператор Гамильтона в ядерном уравнении запишется как: (формула)(7.3).

Первое слагаемое здесь отвечает кинетической энергии для радиальных (колебательных) движений, а второе имеет вид кинетической энергии вращения. μR 2 – это момент инерции ядер относительно центра масс, а L_R 2 – зависящий лишь от полярных углов оператор квадрата углового момента ядер. Если использовать метод разделения переменных и представить волновую функцию ψ(R) в виде произведения функции χ(R), зависящей только от R, и функции Y(θ,ϕ), зависящей лишь от полярных углов (эти функции известны из квантовой механики как сферические гармоники), то нетрудно выписать уравнение для функции χ(R).

К сожалению, в таком понятном рассуждении есть существенный недостаток. В отсутствие внешних полей должен сохраняться полныймомент J всей молекулы как целого, а не только угловой момент ядер. Даже если не учитывать дающий очень малый вклад в энергию ядерный спин, то надо было бы полагать, что сохраняется не LR , а J = L + S + LR. Тем не менее, мы заменим оператор квадрата момента в ядерномуравнении на оператор J 2 (например, ссылаясь на то, что массы ядер намного больше, чем у электронов, а электроны улетают от ядер не слишком далеко. Кроме того, если проделать весьма громоздкие выкладки, приводимое ниже уравнение для радиальной функции тоже получится, но со слегка модифицированным потенциалом). Поскольку момент сохраняется, все состояния молекулы можно классифицировать по собственным значениям оператора квадрата полного момента J 2 , а они равны. Тогда ядерное уравнение (7.1), будет зависеть только от радиальной координаты (такое ядерное уравнение часто называют радиальным уравнением) и запишется, как: (формула) (7.4).

Энергия молекулы ε_n,J,v определяется номером электронного состояния n, вращательным квантовым числом J и номером колебательного состояния v . Напомним, что одним и тем же квадратом момента обладают 2J+1 состояний, различающихся проекцией J_z момента на ось z системы координат. Все эти состояния имеют одну и ту же энергию, то есть вырождены. Разумеется, разным значениям J_z соответствуют разные функции Y_J,Jz , зависящие от угловых переменных и описывающие вращение молекулы. Радиальная функция отвечает условию нормировки (формула) (множитель R 2 возникздесь из-за перехода к сферическим координатам). Поскольку в

таком виде уравнение (7.4) для радиального движения выглядит несколько громоздко, его можно упростить, положив (фомула). Очевидно, условие нормировки для функции u(R) – это обычное условие (формула) =1, а уравнение для неё выглядит как уравнение Шредингера для одной частицы массы μ: (формула) (7.5)

Это уравнение мы будем использовать для описания колебательно-вращательных движений молекулы. Волновую функцию молекулы можно приближенно представить произведением нескольких функций:

а) электронной волновой функции Ф_n(r,R ), получаемой из электронного уравнения Шредингера (4.1),зависящей от радиус-векторов электронов r_j

и их спиновых переменных, а также, как от параметров, от радиус-векторов всех ядер R,

б) волновой функции свободного движения центра масс молекулы — e ± i ( k , Rcm ) ,

в) вращательной части волновой функции Y_J,Jz , зависящей лишь от угловых переменных, описывающих поворот молекулы как целого,

г) колебательной волновой функции u_n,J,v(R) , удовлетворяюшей уравнению (7.5).

При сделанных приближениях энергия молекулы – это сумма энергии свободного движения центра масс (поступательной энергии) и электронно-колебательно-вращательной энергии ε_n,J,v .

Электронно-колебательно-вращательную энергию молекулы можно получить, решая уравнение (7.5). На рисунках 2, 3 приведены результаты численного решения такойзадачи. (Следует отметить, что, решая ур.(7.5) мы определим не только электронно-колебательно-вращательную энергию, но и колебательную волновую функцию u_n,J,v(R), соответствующую этому энергетическому состоянию молекулы.) Для решения уравнения (7.5) необходимо знать функцию En(R) (электронную энергию или потенциал ядерного уравнения), являющуюся решением электронного уравнения Шредингера (4.1). Она может быть задана просто поточечно, однако очень часто потенциал E_n(R) аппроксимируют подходящей аналитической функцией. Вблизи точки минимума (R = Re) электронную энергию можно разложить в ряд, первые члены которого в квадратичном приближении будут иметь вид E_n(R) ≈ E_n(R_e) + k_n(R–R_e) 2 /2 , где k_ne – вторая производная потенциала в точке Re : (формула).При J = 0 уравнение (7.5) с таким потенциалом нетрудно решить, так как это просто задача о

гармоническом осцилляторе: (формула) (8.1)

Значения энергии в такой задаче определяется как: (формула); где

(Формула)– классическая частота колебаний тела массы μ на пружине с силовой постоянной k_e, v – номер колебательного уровня, E_n — электронная энергия данного электронного состояни при равновесном межъядерном расстоянии (Re). Волновые функции u_n,v(R–Re) выражаются как произведение полинома Эрмита и функции вида

exp(–β(R–Re) 2 ) с некоторым коэффициентом β, т.е. быстро спадают при удалении от точки R = Re. Если вернуться к первоначальной задаче с потенциалом En(R) , то с помощью сделанной оценки в гармоническом приближении можно методами теории возмущений вычислить значение энергии колебательного уровня с номером v более точно. При этом оказывается, что поправка к энергии оценивается рядом по степеням величины (v+1/2). В итоге получается ряд, обозначения и выбор знаков коэффициентов (колебательных постоянных) которого – спектроскопическая традиция: (формула) (8.2)

Величина ћω_ex_e(v+1/2) 2 называется поправкой на ангармоничность, а коэффициент ω_e x_e – коэффициентом ангармоничности. Отметим, чтосогласно уравнению. (8.2) с ростом колебательного квантового числа vрасстояние между соседними уровнями энергии становится все меньше и меньше, тогда как в простом гармоническом приближении расстояние между колебательными уровнями остается величиной постоянной. Для аппроксимации функции E_n(R) часто используют потенциала Морзе:(формула). Точное решение ур.(7.5) с таким потенциалом соответствует выражению (8.2), если оборвать ряд на квадратичном по (v+1/2) слагаемом: (формула) (8.3)

Тогда можно найти и явные выражения для гармонической частоты ω_e и коэффициента ангармоничности ω_ex_e через параметры потенциала α и D: (формулы). В этом случае расстояние между колебательными уровнями энергии линейно зависит от v: ε_nv+1 – ε_nv = ћω_e – 2ћω_ex_e(v+1/2) . По выполнению такого линейного соотношения часто судят о применимости модели Морзе. Отметим, что число колебательных состояний для потенциала Морзе конечно ( в отличие от гармонического потенциала) – максимально возможное значение v можно найти из условия ε_nv+1 – ε_nv ≥ 0 , т.е. v≤ω_e/(2ω_ex_e)–1/2 .

Поведение радиальных функций un,0,v(R) колебательных движений ядер (при J = 0) можно понять из рисунка 2. Как видно из рисунка, при малых значениях колебательного квантового числа v волновые функции очень похожи на волновые функции гармонического осциллятора. Для R, отвечающих области, в которой двигалась бы классическая частица, т.е. между точками, в которых энергия частицы равна потенциалу (их называют «точками поворота»), функции осциллируют. В классически запрещенных областях ( где потенциал больше энергии) функции быстро спадают. Важно отметить, что даже при относительно небольших v колебательные волновые функции заметно отличны от нуля возле точек поворота. Это можно объяснить тем, что (по классическим представлениям) наиболее велика вероятность найти частицу в тех областях, где скорость её мала, то есть именно в окрестностях точек поворота. Описанное явление лучше видно на рисунке 3, изображающем распределение ядерной плотности в той же системе.

( 2 жопных не копирующихся рисунка)
Заметив, что волновые функции гармонического осциллятора локализованы возле равновесного расстояния, мы можем применить теорию возмущений и для учета энергии вращения. Применение теории возмущений даст поправки к энергии в виде ряда по степеням J(J+1). Например, в первом порядке теории возмущений надо просто рассмотреть среднее значение оператора (формула) на функциях u_nv(R–Re) гармонического осциллятора. Разложив оцениваемый потенциал в ряд по степеням (R–R_e), находим, что при некоторых коэффициентах с ₂ , с₃,. поправка к энергии имеет вид:

( формула) где B_v , D_v , H_v … являются рядами по степеням (v+1/2).

Выписанное выражение для энергии позволяет, как и в классической модели

молекулы, представить внутреннюю энергию как сумму электронной (E е _n ), колебательной и вращательной энергии: E = E_e + E_vib +E_rot . Состояние молекулы задается указанием электронного состояния (n; обычно указывается символ электронного состояния, например, 2 П), колебательным (v) и вращательным (J) квантовыми числами. В самом грубом приближении (жесткий ротатор) можно пренебречь зависимостью B_v от v и вообще не рассматривать остальные вклады во вращательную энергию.

Понятие «электронная конфигурация». Метод многоконфигурационного самосогласованного поля (МК ССП). Метод конфигурационного взаимодействия (КВ). Одноконфигурационное приближение: метод Хартри-Фока. Понятие «электронная корреляция». Ферми-корреляция и кулоновская корреляция.

Электронная конфигурация — формула расположения электронов по различным электронным оболочкам атома химического элемента или молекулы.

Метод многоконфигурационного взаимодействия (Multi-Configurational Self-Consistent Field – MCSCF) можно рассматривать как метод КВ, в котором оптимизируются не только коэффициенты перед детерминантами, но и коэффициенты разложения МО по АО.

Метод конфигурационного взаимодействия основан на вариационном принципе, аналогично методу Хартри – Фока. Пробная функция записывается в виде линейной комбинации детерминантов, и коэффициенты определяются из условия минимума энергии. Детерминанты классифицируют на однократно (s), дважды (d), трижды (t) и т.д. возбужденные, и функция конфигурационного взаимодействия приобретает следующий вид:

Применяя вариационный принцип, получаем набор секулярных уравнений:

(H — EI)a = 0; (3.5.3)

Здесь H– матрица конфигурационного взаимодействия (КВ),
I – единичная матрица.

Матричный элемент матрицы КВ вычисляется из детерминантов: 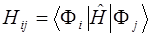. Если два детерминанта отличаются друг от друга более чем двумя пространственными молекулярными орбиталями (МО), то всегда будет существовать интеграл перекрывания между двумя разными МО, который равен нулю. Элементы матрицы КВ могут быть, следовательно, отличны от нуля, если два детерминанта одинаковы или отличаются одной или двумя МО, и они могут быть выражены через интегралы одно- и двухэлектронных операторов и МО. Эти соотношения известны как правила Слэйтера – Кондона. Согласно теореме Бриллюена, матричные элементы между детерминантом Хартри – Фока и однократно возбуждёнными состояниями (детерминантами) равны нулю.

Для вычисления элементов матрицы КВ необходимы одно- (3.5.5) и двухэлектронные (3.5.6) интегралы между МО. Они могут быть выражены через соответствующие интегралы атомных орбиталей (АО) и коэффициенты МО:

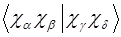
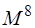
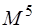
Эти интегралы необходимы для всех методов, учитывающих электронную корреляцию. Двухэлектронные интегралы атомных орбиталей наиболее многочисленны, и соответственно время вычислений пропорционально 8-й степени размера базиса ( ). Однако если выполнять трансформацию одного индекса за раз, то время счёта можно сократить до .

При численной реализации метода КВ сокращают число возбуждённых детерминантов. Включать только однократно возбуждённые детерминанты бессмысленно, так как все матричные элементы между ними и детерминантом Хартри-Фока равны нулю. Только дважды возбуждённые детерминанты дают отличные от нуля матричные элементы. Поэтому самым грубым приближением является включение в расчёт только двукратно возбуждённых детерминантов – модель CID (Configurational Interaction with Doubles). Включение однократно возбуждённых детерминантов даёт модель CISD (CI with Singles and Doubles). Хотя однократно возбуждённые детерминанты и дают нулевые матричные элементы с детерминантом Хартри-Фока, но они дают отличные от нуля матричные элементы с двукратно возбуждёнными детерминантами. Для больших базисов время счёта методом CISD пропорционально 6-й степени размера базиса ( ).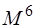

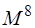
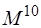
Следующая ступень улучшения – включение трижды возбуждённых детерминантов – метод CISDT (время счёта пропорционально ). Для метода CISDTQ время счёта пропорционально . Метод CISDTQ даёт результат, близкий к методу полного учёта КВ, но он применим только к небольшим молекулам. Единственный метод, широко применяемый для больших систем в настоящее время, – это CISDT. Он учитывает порядка 80-90% корреляционной энергии, хотя с увеличением размера молекулы процент учёта корреляционной энергии уменьшается

Метод Хартри – Фока даёт правильное решение на 99%, и логично его использовать за основу для дальнейшего улучшения. В общем мультидетерминантную функцию можно записать в следующем виде:

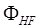
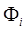
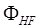
Здесь коэффициент а₀ обычно близок к единице; – детерминант Слэйтера, используемый в методе Хартри – Фока; – возбуждённый детерминант Слэйтера, получаемый из заменой одной или нескольких связывающих молекулярных орбиталей на виртуальные, что соответствует возбуждённой конфигурации.

Недостатком метода Хартри – Фока является представление о движении электрона в усредненном поле всех остальных электронов. Но движение электронов является взаимозависимым – электроны стремятся расположиться как можно всегда дает завышенное значение общей энергии. Разность между энергией, вычисленной методом Хартри – Фока, и минимальной энергией, которую можно рассчитать в данном базисе, называется энергией электронной корреляции. дальше друг от друга вкаждый момент времени. В результате электроны в среднем располагаются несколько дальше друг от друга в сравнении с моделью усредненного поля Хартри, что снижает энергию их взаимодействия. Поэтому метод Хартри – Фока. Электронная корреляция – эффект, обусловленный мгновенным кулоновским отталкиванием между электронами (стремлением электронов «избежать друг друга»). Его учет приводит к более низкому значению полной энергии системы. Не учитывается в методе Хартри-Фока. Изменение энергии, вызванное этими мгновенными кулоновскими взаимодействиями, называется энергией корреляции: Eкорреляц. = Eточн. — EХФ (0) , например функции водородоподобного атома. С исходным набором функций рассчитывают óстовный и кулоновский интегралы, а затем решаются уравнения для каждого значения i. Другими словами, решается задача на собственные значения и собственные вектора оператора Хартри, который приближённо считается равным оператору Гамильтона.

Найденные функции 1-го приближения Ψ_j (1) используются вновь для расчёта óстовного и кулоновского интегралов, и процедура повторяется – вычисляют функции Ψ_j (2) , Ψ_j (3) , … и соответствующие им энергии E (2) , E (3) , … . Повторение вычислений проводят до тех пор, пока для функций Ψ_j ( n ) и Ψ_j ( n +1) величины эффективных потенциалов (и соответствующие им энергии E ( n ) и E ( n +1) ) не будут совпадать с заданной точностью. Это требование обусловливает название метода самосогласованного поля (ССП, SCF – Self-Consistent Field).

Недостатком метода Хартри является неправильный вид общей волновой функции, представленной в виде произведения одноэлектронных функций (3.2.6). Электроны являются фермионами – частицами с полуцелым спином, и, в соответствии с принципом Паули, система из нескольких электронов должна описываться антисимметричной волновой функцией. Это значит, что при перестановке двух электронов функция должна менять знак на противоположный: .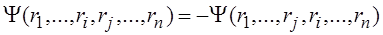

Поэтому Владимир Александрович Фок* усовершенствовал метод Хартри, предложив антисимметричную общую волновую функцию в виде определителя Слэйтера, составленного из ортонормированных ( 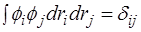) одноэлектронных функций:

📺 Видео

Урок 32. Уравнение ШрёдингераСкачать

Уравнение ШрёдингераСкачать

Лекция №4 "Волновая функция. Уравнение Шредингера" (Гавриков А.В.)Скачать

Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Классические уравнения | уравнение Шрёдингера (координатное представление) | простейший выводСкачать

10. Уравнение ШрёдингераСкачать

Квантовая механика 41 - Уравнение Шредингера. Гамильтониан.Скачать

Консультация по квантовой механике. Часть 5. "Волновая функция. Уравнение Шредингера"Скачать

Уравнение Шредингера Стационарные состоянияСкачать

Теория Бора. Гипотеза де Бройля. Принцип неопределенности. Уравнение Шрёдингера.Скачать

Пример. Численное решение радиального уравнения Шредингера (одноточечная разностная схема)Скачать

Сущёв И. - Квантовая теория. Ч.2 - 1. Численные методы решения уравнения ШрёдингераСкачать

Воронина Е. Н. - Атомная физика. Семинары - Решение уравнения Шредингера для потенциальной ямыСкачать

Новаковская Ю. В. - Строение молекул - Молекулярная задачаСкачать

Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

7.1 Разделение переменных в уравнении ШрёдингераСкачать