Какие модели наблюдения соответствуют модельному и выборочному уравнению регрессии (6 видео)

МОДЕЛИ И МЕТОДЫ РЕГРЕССИОННОГО АНАЛИЗА

В результате изучения данной главы читатель должен:

• задачи, области и возможности применения методов и моделей регрессионного анализа;
• принципы, предпосылки, этапы и методы построения регрессионных моделей;

• использовать регрессионные модели в решении задач оптимизации функционирования социально-экономических систем разного уровня;
• оценивать адекватность и статистическую значимость регрессионных моделей;
• анализировать и интерпретировать основные результаты регрессионного анализа и предлагать на этой основе практические рекомендации по повышению эффективности функционирования социально-экономических структур;

• навыками построения парных и многофакторных линейных и нелинейных регрессионных моделей;
• навыками проведения прогнозных расчетов на основе регрессионного анализа;
• навыками использования статистических программ R, SPSS, PSPP для построения регрессионных моделей разных видов.

Содержание

Модели парной и множественной регрессии
Оценка параметров регрессионной модели
Регрессия в эконометрике
Регрессия и ее виды
Предпосылки регрессионного анализа
Готовые работы на аналогичную тему
Парная регрессионная модель
🎦 Видео

Видео:Множественная регрессияСкачать

Модели парной и множественной регрессии

Корреляционный анализ может дать представление о степени связи, но не о ее виде. Для анализа воздействия на результативный признак одного или нескольких факторных признаков используется регрессионный анализ, который считается основным методом математической статистики для выявления неявных и завуалированных связей между результатами измерений [6].

Если выявленные на основе корреляционного анализа связи между изучаемыми признаками окажутся существенными (т.е. достаточно сильными и статистически значимыми), то целесообразно найти их математическое выражение в виде регрессионной модели и оценить ее адекватность. Адекватная регрессионная модель может использоваться для прогнозирования изучаемого явления или показателя.

Таким образом, задачами регрессионного анализа являются определение формы связи (выбор и построение модели), установление степени влияния факторов на результативный признак и прогнозирование значений зависимой переменной.

Регрессионный анализ заключается в подборе соответствующей аппроксимирующей функции для имеющегося набора наблюдений. Аппроксимация (от лат. approximo — приближаюсь) — это приближенное выражение эмпирических данных в виде функции. Полученная функциональная зависимость называется уравнением регрессии, или просто регрессией. Более строго, регрессия — это зависимость среднего значения какого-либо признака от среднего значения других (одного или нескольких) признаков.

Регрессия называется парной, если она описывает зависимость между функцией и одной переменной, т.е. имеет вид у =/(#). Регрессия называется множественной, если она включает в себя несколько переменных и имеет вид у = f(x_v х₂. х_п).

Если уравнение регрессии линейное, т.е. имеет вид у = а_хх + а₀ (для одной переменной) или у = а_<х_< + ajc₂ + ••• + а ,Р с _п + а о (Д ля п переменных), регрессия называется линейной, иначе — нелинейной.

Важнейшим этапом построения регрессионной модели (уравнения регрессии) является установление в исходных эмпирических данных некой закономерности и ее выражение в виде математической функции. Сложность заключается в том, что из множества функций необходимо найти такую, которая лучше других выражает реально существующие связи между анализируемыми признаками (т.е. необходимо найти такую функцию, которая наилучшим образом аппроксимирует имеющиеся данные). Выбор типов функции может опираться на теоретические знания об изучаемом явлении, опыт предыдущих аналогичных исследований или осуществляться эмпирически — перебором и оценкой функций разных типов.

Для подбора аппроксимирующей функции решается следующая задача (для простоты рассмотрим случай парной регрессии, когда имеется лишь один факторный признак). Известен набор из п измерений результативного признака у при разных значениях факторного признака х. (x_jf y_t), i = 1. п. Пусть имеется ряд функций (линейные, квадратичные, экспоненциальные и т.д.). Требуется выбрать такую функцию г/ =f(x) из имеющихся, чтобы ее значения у_> для набора x_i наилучшим образом приближали значения у.. Значения г/, называются теоретическими (ожидаемыми) значениями, а значения у- — эмпирическими (наблюдаемыми).

Что значит «наилучшим образом»? В качестве критерия, насколько одна функция лучше другой, используется набор разностей#, — y_t. Очевидно, что выбором функции# = f(x) их нужно сделать как можно меньшими. Но для сравнения качества аппроксимации просто складывать разности нельзя, ведь они могут иметь разные знаки, и тогда ошибки могут взаимно компенсироваться. Поэтому выбирают сумму квадратов разностей, которая должна быть минимизирована:

По этой причине такой метод называется методом наименьших квадратов (МНК), он был предложен немецким математиком К. Гауссом в 1794 г. Фактически этот метод реализован как метод решения систем уравнений.

Проиллюстрируем использование МНК на простейшем примере парной линейной регрессии. Уравнение однофакторного линейного регрессионного уравнения имеет вид где у — теоретические значения результативного признака, полученные по уравнению регрессии; я₀, я, — коэффициенты (параметры) уравнения регрессии. Значение я₀ соответствует теоретическому значению у при х = 0. Коэффициент я, показывает среднюю величину изменения результативного признака у при изменении факторного признаках на единицу, т.е. вариацию у, приходящуюся на единицу вариации х. Знак я, указывает направление этого изменения.

Параметры регрессионного уравнения я₀, я, находят из условия минимальности сумм квадратов отклонений эмпирических данных y_i от теоретических у:

Графическая иллюстрация этого подхода представлена на рис. 9.1.

Рис. 9.1. Иллюстрация метода МНК

Таким образом, должна минимизироваться функция двух переменных

/(я₀, я,) = ? <у,— я₀ — я,х,) 2 . Для этого первые частные производные функ- 1-1

ции/(я₀, я,) по аргументам я₀ и я, приравниваются к нулю, и в результате получается система двух линейных уравнений

Решение этой системы дает значение коэффициентов регрессии в общем виде:

Технически более удобно вычислять параметры уравнения парной линейной регрессии по следующим формулам, дающим тот же результат:

Метод легко обобщается на случай множественной линейной и нелинейной регрессии. Если, например, в качестве аппроксимирующей функции выбирается квадратичная зависимость вида

то минимизироваться должна функция трех переменных

Чтобы найти значения коэффициентов регрессии, нужно вычислить первые частные производные функции f(a₀, a_v а₂) по аргументам а₀, a_v и я₂, приравнять их к нулю и решить систему трех уравнений с тремя неизвестными.

Но при использовании МНК для определения параметров регрессии многих переменных возрастают техническая сложность и объем расчетов из-за увеличения числа переменных и уравнений, поэтому регрессионный анализ целесообразно осуществлять с помощью общепользовательских или специальных программных средств. Например, можно использовать соответствующие стандартные функции MS Excel или процедуры PSPP, более удобные и содержательные с точки зрения отчетов о результатах (см. далее).

Если зависимая и независимые переменные представлены в стандартной 2-шкале (см. параграф 7.3), то коэффициенты уравнения регрессии у = PjXj + р₂ х 2 + ••• + Ра + а о называются стандартными коэффициентами регрессии, или р-коэффициентами. Знак p-коэффициента соответствует знаку корреляции между зависимой переменной и данной независимой переменной. Если p-коэффициент положителен, то связь этой переменной с зависимой переменной прямая, если отрицателен — то обратная. По абсолютной величине p-коэффициента можно судить о влиянии данной независимой переменной на зависимую: чем больше коэффициент но абсолютному значению, тем сильнее это влияние, т.е. тем выше информативность этой переменной для прогнозирования значений результативного признака. Если p-коэффициент близок к нулю, связь между переменными отсутствует. В случае парной регрессии p-коэффициент в точности равен коэффициенту корреляции между результативным и факторным признаками.

При изучении связи социальных и экономических показателей помимо линейных моделей используют различного вида нелинейные уравнения. Во многих случаях нелинейные связи линеаризуют, т.е. приводят к линейному виду (путем логарифмирования, замены переменных и т.д.). Такая процедура называется линеаризацией. Например, при полиномиальной связи можно добавить дополнительную переменную.

Пример 9.1. При помощи соответствующих трансформаций в линейную регрессионную модель можно перевести различные нелинейные связи. К примеру, очень часто встречающуюся экспоненциальную связь у = ае Ьх можно преобразовать в линейную при помощи логарифмирования: ln(z/) = In (а) + bx.

Если в качестве аппроксимирующей функции выбирается зависимость

то замена переменных z = /у дает линейную зависимость z = а₀ + а_<х. Если у = = (а₀ + а_хх) 2 , то замена z= Jy опять приводит к линейной зависимости z = а₀ + а_<х.

В микроэкономике используется производственная функция Кобба — Дугласа, связывающая объем выпуска продукции /с затратами капитала К и труда L:

При этом предполагается, что параметры аир одни и тс же для предприятий одной отрасли. Поэтому знание этих параметров позволит прогнозировать объем производства для разных значений К и L. Для оценки этих параметров можно собрать информацию по п предприятиям отрасли об объемах производства, затратах капитала и труда на этих предприятиях и по этим данным построить регрессионную модель. При этом функцию Кобба — Дугласа можно линеаризовать путем ее логарифмирования:

После замены переменных и соответствующего преобразования исходных данных x_i = InK_jt y_t = In L_jt z_i = In/ для всех i = 1. n получаем линейное регрессионное уравнение z = or + py> из которого получаются оценки а и р.

Связи, которые при помощи соответствующих трансформаций могут быть переведены в линейную модель, называются линейными по существу <intrinsically linear model).Параметры регрессионных моделей, линейных по существу, вычисляются методом МНК, т.е. непосредственно решением соответствующей системы уравнений. Для нелинейных моделей, которые нельзя линеаризовать, в пакете SPSS существует итерационная процедура оценки коэффициентов нелинейной регрессионной модели.

Применение регрессионного анализа предполагает выполнение ряда предпосылок. Хотя многие из этих предпосылок нельзя проверить точно, исследователь должен провести хотя бы приблизительную оценку их выполнения и сделать обоснованный вывод о величине отклонений от этих предпосылок и возможности проведения регрессионного анализа. Чем сильнее отклонение от предпосылок-допущений, тем менее надежными могут оказаться результаты анализа и тем с большей осторожностью к ним следует относиться.

Первое требование — отсутствие сильных линейных взаимосвязей между независимыми переменными регрессионной модели (неслучайно они называются независимыми). Наличие таких связей называется мультиколли- пеариостыо. Эффект мультиколлииеарности означает, что по крайней мере одна из независимых переменных, включенных в модель, является лишней (модель избыточна). Кроме того, мультиколлинеарность может привести к ложным корреляциям (см. гл. 8). При мультиколлииеарности снижаются точность оценки параметров регрессионной модели и точность прогноза на ее основе, возрастают ошибки оценок некоторых параметров модели, эти оценки становятся неустойчивыми: добавление или исключение нескольких наблюдений приводит к значительным изменениям в оценках. Интерпретация коэффициентов регрессионного уравнения при эффекте мультиколлинеарности также может быть затруднена. Проиллюстрируем эффект мультиколлииеарности на очень простом, но весьма характерном примере.

Пример 9.2. Предположим, определяется наличие связи между ростом человека и длиной ступни. В качестве результативного признака выберем рост, а в качестве факторного признака — длину ступни. Очевидно, что такая связь должна наблюдаться, но что получится, если в качестве переменных регрессионной модели использовать длину левой ступни и правой ступни? Если строится линейная регрессионная модель и коэффициенты перед переменными положительны, то их следует интерпретировать так: при увеличении длины левой ступни на 1 см рост увеличивается в среднем на с/, сантиметров, а при увеличении длины правой ступни на 1 см рост увеличивается в среднем на я₂ сантиметров. Если я, и я₂ отличаются друг от друга (что весьма вероятно), то подобная интерпретация выглядит абсурдной. Еще более абсурдной будет интерпретация, если коэффициенты будут иметь разные знаки (что также не исключено). В таком случае из модели будет следовать, что с увеличением длины одной ступни рост увеличивается, а с увеличением длины другой — уменьшается! Такие абсурдные выводы получаются из-за тесной связанности переменных, включенных в модель, т.е. когда две или более переменных содержат одинаковую (как в данном примере) или приблизительно одинаковую информацию для объяснения результативного признака.

Самый простой способ выявить эффект мультиколлинеарности — определить коэффициенты корреляции между переменными, которые предполагается включить в регрессионную модель в качестве факторных признаков. Следует избегать включения в модель переменных, между которыми обнаруживается сильная корреляционная связь (г> 0,7). Как правило, эффект мультиколлинеарности приводит к тому, что по ряду статистических показателей регрессионная модель не может считаться статистически значимой (надежной).

Второе требование — переменные модели должны иметь распределение, близкое к нормальному (статистически незначительно отличающееся от нормального). Хотя отклонение от этого предположения не критично для проведения регрессионного анализа, тем не менее, прежде чем сделать окончательные выводы, следует рассмотреть распределения представляющих интерес переменных с помощью соответствующих статистических критериев (см. параграф 7.4).

Третье требование — результативный и факторные признаки должны быть измерены в метрической шкале. Однако на практике выполнение этого требования не всегда можно обеспечить. Поэтому считается допустимым, чтобы результативный признак измерялся в метрической шкале, а факторные — по крайней мере в порядковой шкале.

Довольно часто в регрессионную модель включаются переменные и в номинативной шкале (например, переменная «пол», принимающая значения 0 и 1). Такие переменные называются фиктивными переменными (dummy variables), или индикаторами. Коэффициенты перед соответствующей фиктивной переменной показывают, насколько в среднем изменяется значение результативного признака при включении того или иного факторного признака, измеренного в номинативной шкале, по сравнению с отсутствием этого признака (присутствием другого признака).

Видео:Математика #1 | Корреляция и регрессияСкачать

Оценка параметров регрессионной модели

ГЛАВА 3. МОДЕЛЬ МНОЖЕСТВЕННОЙ

ЛИНЕЙНОЙ РЕГРЕССИИ

Основные понятия и уравнения множественной регрессии

На любой экономический показатель чаще всего оказывает влияние не один, а несколько совокупно действующих факторов. Например, объем реализации (Y) для предприятий оптовой торговли может определяться уровнем цен (Х₁), числом видов товаров (Х₂), размером торговой площади (Х₃) и товарных запасов (Х₄). В целом объем спроса на какой-либо товар определяется не только его ценой (Х₁), но и ценой на конкурирующие товары (Х₂), располагаемым доходом потребителей (Х₃), а также некоторыми другими факторами. Показатель инновационной активности современных предприятий зависит от затрат на исследования и разработки (Х₁), на приобретение новых технологий (Х₂), на приобретение программных продуктов и средств (Х₃) и обучение и переподготовку кадров [7,28]. В этих случаях возникает необходимость рассмотрения моделей множественной (многофакторной, многомерной) регрессии [28].

Модель множественной линейной регрессии является естественным обобщением парной (однофакторной) линейной регрессионной модели. В общем случае ее теоретическое уравнение имеет вид:

(3.1)

где Х₁, Х₂,…, Х_m – набор независимых переменных (факторов-аргументов); b₀, b₁, …, b_m – набор (m + 1) параметров модели, подлежащих определению; ε – случайное отклонение (ошибка); Y – зависимая (объясняемая) переменная.

Для индивидуального i-го наблюдения (i = 1, 2, …, n) имеем:

(3.2)

. (3.3)

Здесь b_j называется j—м теоретическим коэффициентом регрессии (частичным коэффициентом регрессии).

Аналогично случаю парной регрессии, истинные значения параметров (коэффициентов) b_j по выборочным данным получить невозможно. Поэтому для определения статистической взаимосвязи переменных Y и Х₁, Х₂, …, Х_m оценивается эмпирическое уравнение множественной регрессионной модели

(3.4)

в котором , – оценки соответствующих теоретических коэффициентов регрессии; е – оценка случайного отклонения ε.

Оцененное уравнение (3.4) в первую очередь должно описывать общий тренд (направление, тенденцию) изменения зависимой переменной Y. При этом необходимо иметь возможность рассчитать отклонения от этого тренда.

Для решения задачи определения оценок параметров множественной линейной регрессии по выборке объема n необходимо выполнение неравенства n ³ m + 1 (m – число регрессоров). В данном случае число v = n — m — 1 будет называться числом степеней свободы. Отсюда для парной регрессии имеем v = n — 2. Нетрудно заметить, что если число степеней свободы невелико, то и статистическая надежность оцениваемой формулы невысока. На практике принято считать, что достаточная надежность обеспечивается в том случае, когда число наблюдений по крайней мере в три раза превосходит число оцениваемых параметров k = m + 1. Обычно, статистическая значимость парной модели наблюдается при n ≥ 7.

Самым распространенным методом оценки параметров уравнения множественной линейной регрессионной модели является метод наименьших квадратов (МНК). Напомним (см. раздел 2.4.1), что надежность оценок и статистических выводов, полученных с использованием МНК, обеспечивается при выполнении предпосылок Гаусса-Маркова. В случае множественной линейной регрессии к предпосылкам 1–4 необходимо добавить еще одну (пятую) – отсутствие мультиколлинеарности, что означает отсутствие линейной зависимости между объясняющими переменными в функциональной или статистической форме. Более подробно мультиколлинеарность объясняющих переменных будет рассмотрена в разделе (3.4). Модель, удовлетворяющая предпосылкам МНК, называется классической нормальной моделью множественной регрессии.

На практике часто бывает необходимо оценить силу влияния на зависимую переменную различных объясняющих (факторных) переменных. В этом случае используют стандартизованные коэффициенты регрессии и средние коэффициенты эластичности .

Стандартизированный коэффициент регрессии определяется по формуле:

(3.5)

где S(x_j) и S(y) – выборочные средние квадратичные отклонения (стандарты) соответствующей объясняющей и зависимой переменных.

Средний коэффициент эластичности

(3.6)

показывает, на сколько процентов (от средней) изменится в среднем зависимая переменная Y при увеличении только j-й объясняющей переменной на 1 %.

Для модели с двумя объясняющими (факторными) переменными , после нахождения оценок , уравнение определяет плоскость в трехмерном пространстве. В общем случае m независимых переменных геометрической интерпретацией модели является гиперплоскость в гиперпространстве.

Оценка параметров регрессионной модели

Для нахождения оценок параметров b_j множественной линейной регрессионной модели (коэффициентов эмпирического уравнения регрессии) используется метод наименьших квадратов (МНК). Суть МНК заключается в минимизации суммы квадратов отклонений наблюдаемых выборочных значений y_i зависимой переменной Y от их модельных оценок . Отклонение е_i, соответствующее уравнению регрессии в i-м наблюдении (i = 1, 2, …, n), рассчитывается по формуле:

. (3.7)

Тогда для нахождения коэффициентов 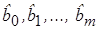по МНК минимизируется следующая функция m + 1 переменных:

. (3.8)

Необходимым условием минимума функции G является равенство нулю всех ее частных производных по Частные производные квадратичной функции (3.8) являются линейными функциями относительно параметров:

. (3.9)

Приравнивая (3.9) к нулю, получаем систему m + 1 линейных нормальных уравнений с m + 1 неизвестными для определения параметров модели:

(3.10)

где j = 1, 2, …, m – определяет набор регрессоров.

Следует заметить, что включение в модель новых объясняющих переменных усложняет расчет коэффициентов множественной линейной регрессии путем решения системы (3.10) по сравнению с парной моделью. Система из трех уравнений, соответствующая модели с двумя объясняющими переменными , может быть легко решена методом определителей. Однако в общем виде решение системы (3.10) и анализ множественной регрессионной модели наиболее целесообразно проводить в векторно-матричной форме [15,17].

Тогда, вводя матричные обозначения, запишем:

, , .

Здесь Y – n-мерный вектор-столбец наблюдений зависимой переменной; Х – матрица размерности n · (m + 1) значений объясняющих переменных x_ij, в которой единица соответствует переменной при свободном члене ; – вектор-столбец размерности m + 1 оценок параметров модели (коэффициентов уравнения регрессии); е – вектор-столбец размерности n отклонений выборочных (реальных) значений y_i зависимой переменной, от значений оценок , получаемых по уравнению регрессии.

В матричной форме модель (3.1) примет вид:

Оценкой этой модели по выборочным данным является уравнение (эмпирическая модель)

. (3.12)

Предпосылки МНК (см. раздел 2.4.1.) в матричной форме можно записать следующим образом:

1. M(e) = 0; 2. D(e) = σ 2 I; 3. Матрица ковариаций V(e) = M(e · e T ) = σ 2 E,

где e = – вектор-столбец случайных отклонений (ошибок);

I = – (n · 1) вектор;

E = E_n_×_n = – единичная матрица;

– матрица ковариаций или ковариационная матрица вектора случайных отклонений, которая является многомерным аналогом дисперсии одной переменной и в которой, если предпосылка о некоррелированности отклонений e_i и e_j выполняется, все элементы, не лежащие на главной диагонали, равны нулю, а элементы главной диагонали равны одной и той же дисперсии D(e_i) = σ 2 ; 4. e – нормально распределенный случайный вектор, т. е. e

N(0, σ 2 Е); 5. r(X) = m + 1 > n – детерминированная матрица объясняющих переменных (регрессоров) имеет ранг r, равный числу определяемых параметров модели m + 1, кроме того, число имеющихся наблюдений каждой из объясняющих переменных и зависимой переменной превосходит ранг матрицы Х.

Выполнение пятой предпосылки означает линейную независимость объясняющих переменных (линейную независимость столбцов матрицы Х), т. е. отсутствие функциональной мультиколлинеарности.

Наша задача заключается в нахождении вектора оценок по МНК, который, при выполнении предпосылок 1–5, обладает наименьшим рассеянием относительно параметра B.

Воспользовавшись известными соотношениями матричной алгебры и правилами дифференцирования по векторному аргументу, получим необходимое условие минимума функции G (равенство нулю вектор-столбца частных производных )

(3.13)

откуда вытекает система нормальных уравнений в матричной форме для определения вектора

(3.14)

где Х Т – транспонированная матрица.

Решением уравнения (3.14) является вектор оценок:

(3.15)

где (Х Т Х) — 1 – матрица, обратная Х Т Х; Х Т Y – вектор-столбец свободных членов системы.

Найдем матрицы, входящие в матричное уравнение (3.14):

. (3.16)

Матрица Х Т Х образует симметричную матрицу сумм первых степеней, квадратов и попарных произведений n наблюдений объясняющих переменных.

. (3.17)

Матрица Х Т Х представляет вектор-столбец произведений n наблюдений объясняющих и зависимой переменных.

Зная вектор коэффициентов множественной линейной регрессии (3.15), находим оценку (групповую среднюю) зависимой переменной Y при заданном векторе значений объясняющей (факторной) переменной [11,28].

Пример 3.1. Для иллюстрации получим формулы для расчета коэффициентов парной регрессии (m = 1), используя матричные обозначения.

В соответствии с (3.17) определим матрицу А — 1 = (Х Т Х) — 1 по формуле:

где detA – определитель матрицы Х Т Х; A * – присоединенная матрица (транспонированная матрица алгебраических дополнений).

Для данного примера:

, .

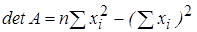
Тогда вектор оценок для частного случая m = 1 определяется как:

откуда следуют формулы (2.11) для определения параметров парной регрессионной модели.

Видео:Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать

Регрессия в эконометрике

Вы будете перенаправлены на Автор24

Видео:Парная регрессия: линейная зависимостьСкачать

Регрессия и ее виды

Регрессионный анализ – это основной математико-статистический инструмент в эконометрике. Регрессия представляет собой зависимость среднего значения величины $y$ от другой величины $x$ или же нескольких величин $x_i$.

Количество факторов, которые включены в равнение регрессии, определяет вид регрессии, которая может быть простой (парной) и множественной.

Простая регрессия – это модель, в которой среднее значение зависимой переменной y является функцией одной независимой переменной x.

Парная регрессия в неявном виде – это уравнение вида:

В явном виде: $y ̂= a + bx$, где $a$ и $b$ – это оценки коэффициента регрессии.

Множественной регрессией является модель, в которой среднее значение объясняемой переменной $y$ – это функция нескольких объясняющих переменных $x_1, x_2, …, x_n$. Множественная регрессия в неявном виде – это модель типа:

$y ̂= f(x_1, x_2,…, x_n)$

В явном виде: $y ̂= a + b_1x_1 + b_2x_2 + … + b_nx_n$

Примером модели множественной регрессии может выступать зависимость зарплаты работников от их возраста, уровня образования, степени квалификации, стажа работы, отрасли и т.д.

Относительно формы регрессия может быть линейной и нелинейной, предполагающей наличие нелинейных соотношений среди факторов. В большинстве случаев нелинейные модели можно привести к линейному виду.

Видео:Простые показатели качества модели регрессии (R2, критерии Акаике и Шварца)Скачать

Предпосылки регрессионного анализа

Чтобы проведение регрессионного анализа было наиболее результативным, необходимо выполнять определенные условия:

В любом наблюдении математические ожидания случайной ошибки должны быть равны нулю;
Дисперсия случайной ошибки для всех наблюдений должна быть постоянной;
Случайные ошибки не должны иметь между собой статической зависимости;
Объясняющая переменная x должна быть величиной неслучайной.

Если выполняются все вышеперечисленные условия, то модель является линейной классической регрессионной. Рассмотрим подробнее предположения и условия, составляющие основу регрессионного анализа.

Готовые работы на аналогичную тему

Согласно первому условию, случайная ошибка не должна систематически смещаться. Если в уравнении регрессии имеется постоянный член, то данное условие автоматически выполняется.

Второе условие – это наличие в каждом наблюдении только одного значения дисперсии случайной ошибки. Дисперсия – это возможное изменение случайной ошибки до проведения выборки. Величина дисперсии является неизвестной, а задача регрессионного анализа – это ее оценка. Независимость дисперсии случайных ошибок от номера наблюдения – это гомоскедастичность, т.е. одинаковый разброс. Гетероскедастичность – это зависимость дисперсии случайных ошибок от номера наблюдения.

Если не выполняется условие гомоскедастичности, то оценка коэффициентов регрессии будет неэффективной.

Третье условие состоит в некоррелированности случайных отклонений для различных наблюдений. Данное условие часто не выполняется при ситуации, когда данные – это временные ряды. Если оно не выполняется, то это означает автокорреляцию остатков. Чтобы диагностировать и устранить автокорреляцию, существуют специальные методы.

Четвертое условие представляет особую важность, поскольку если не выполняется условие неслучайности объясняющих переменных, то оценка коэффициентов регрессии будет смещенной и несостоятельной. Данное условие нарушается при ошибках в измерении объясняющих переменных или же при использовании лаговых переменных.

Видео:Эконометрика. Линейная парная регрессияСкачать

Парная регрессионная модель

Как правило в естественных науках рассматриваются функциональные зависимости, в которых каждое значение одной переменной соответствует единственному значению другой. Однако в экономических переменных нет таких зависимостей, но есть статистические и корреляционные зависимости.

Наибольшую опасность в парной регрессии представляют ошибки в измерениях. Если ошибки спецификации возможно уменьшить с помощью изменения формы модели, ошибки выборки – при помощи увеличения объема исходных данных, то ошибки изменения невозможно исправить.

Случайный фактор в регрессионных моделях может отсутствовать по следующим причинам:

В модель не включены все объясняющие переменные. Любая модель эконометрики – это упрощение реальной ситуации, которая является сложнейшим переплетением факторов, большинство из которых не учитываются в модели, из-за чего реальные значения зависимой переменной отклоняются от модельных значений. Невозможно перечислить все виды объясняющих переменных, поскольку неизвестно заранее, какие факторы относятся к определяющим, а какие можно не учитывать.
Неправильное определение функционального типа модели. Слабая изученность исследуемого процесса, его переменчивость влияет на правильность подбора его моделирующей функции. Это отражается и на отклонении модели от реальной жизни.
Агрегирование переменных. Многие модели содержат зависимость между факторами, являющимися комбинацией других переменных. Например, чтобы рассмотреть в качестве зависимой переменной совокупный спрос, необходимо провести анализ зависимости, содержащей объясняемую переменную, являющуюся композицией индивидуальных спросов, которые оказывают влияние на нее. Это может послужить причиной отклонения значений реальных от модельных.
Ошибки в измерениях. Даже при качественной модели ошибки в измерениях сказываются на несоответствии получаемых значений эмпирическим.
Ограниченность статистической информации. Часто строятся модели, которые являются непрерывными функциями. Для этого применяется информация, имеющая дискретную структуру. Данное несоответствие выражается в случайном отклонении.
Непредсказуемость человеческих факторов. Данная причина может исказить любую качественную эконометрическую модель, поскольку даже правильный выбор формы модели, скрупулезный подбор объясняющих переменных не позволяют спрогнозировать поведение индивидов.