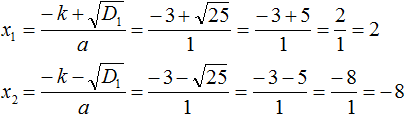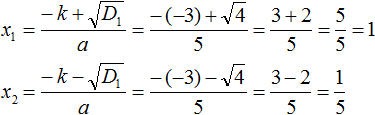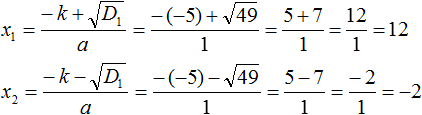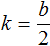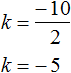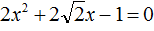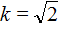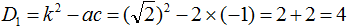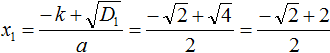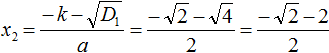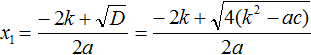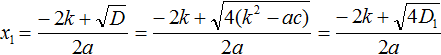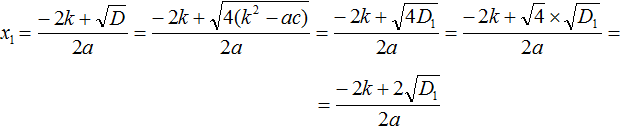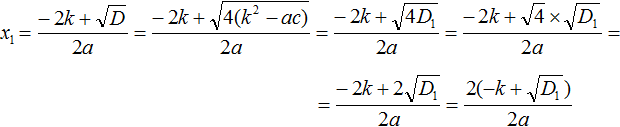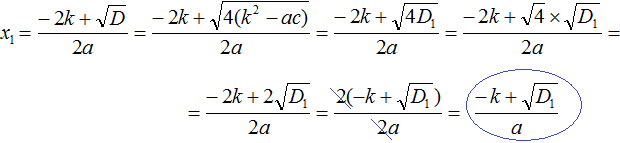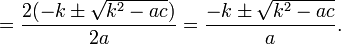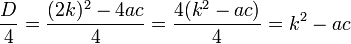Если в квадратном уравнении ax 2 + bx + c = 0 второй коэффициент b является чётным, то решение этого уравнения можно немного упростить. Дискриминант для такого уравнения можно вычислить по формуле D1 = k 2 − ac , а корни по формулам 
и 
.
Видео:Квадратное уравнение с четным вторым коэффициентом. Вывод формулыСкачать
Примеры
Решим квадратное уравнение x 2 + 6x − 16 = 0 . В нём второй коэффициент является чётным. Чтобы воспользоваться формулами для чётного коэффициента, нужно сначала узнать чему равна переменная k .
Любое четное число n можно представить в виде произведения числа 2 и числа k , то есть 2k .
Например, число 10 можно представить как 2 × 5 .
В этом произведении k = 5 .
Число 12 можно представить как 2 × 6 .
В этом произведении k = 6 .
Число −14 можно представить как 2 × (−7)
В этом произведении k = −7 .
Как видим, сомножитель 2 не меняется. Меняется только сомножитель k .
В уравнении x 2 + 6x − 16 = 0 вторым коэффициентом является число 6 . Это число можно представить как 2 × 3 . В этом произведении k = 3 . Теперь можно воспользоваться формулами для чётного коэффициента.
Найдем дискриминант по формуле D1 = k 2 − ac
Теперь вычислим корни по формулам: и .
Значит корнями уравнения x 2 + 6x − 16 = 0 являются числа 2 и −8 .
В отличие от стандартной формулы для вычисления дискриминанта ( D=b 2 − 4ac ), в формуле D1 = k 2 − ac не нужно выполнять умножение числа 4 на ac .
И в отличие от формул 
и 
формулы и не содержат в знаменателе множитель 2 что опять же освобождает нас от дополнительных вычислений.
Пример 2. Решить квадратное уравнение 5x 2 − 6x + 1=0
Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−3) . То есть k = −3 . Найдём дискриминант по формуле D1 = k 2 − ac
Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и
Пример 3. Решить квадратное уравнение x 2 − 10x − 24 = 0
Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−5) . То есть k = −5 . Найдём дискриминант по формуле D1 = k 2 − ac
Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и
Обычно для определения числа k поступают так: делят второй коэффициент на 2.
Действительно, если второй коэффициент b является чётным числом, то его можно представить как b = 2 k . Чтобы из этого равенства выразить сомножитель k , нужно произведение b разделить на сомножитель 2
Например, в предыдущем примере для определения числа k можно было просто разделить второй коэффициент −10 на 2
Пример 5. Решить квадратное уравнение 
Коэффициент b равен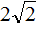 
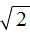
. Это выражение состоит из множителя 2 и выражения 
. То есть оно уже представлено в виде 2k . Получается, что 
Найдём дискриминант по формуле D1 = k 2 − ac
Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и
При вычислении корня уравнения получилась дробь, в которой содержится квадратный корень из числа 2. Квадратный корень из числа 2 извлекается только приближённо. Если выполнить это приближённое извлечение, а затем сложить результат с 2, и затем разделить числитель на знаменатель, то получится не очень красивый ответ.
В таких случаях ответ записывают, не выполняя приближённых вычислений. В нашем случае первый корень уравнения будет равен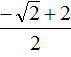 
.
Вычислим второй корень уравнения:
Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать
Вывод формул
Давайте наглядно увидим, как появились формулы для вычисления корней квадратного уравнения с чётным вторым коэффициентом.
Рассмотрим квадратное уравнение ax 2 + bx + c = 0 . Допустим, что коэффициент b является чётным числом. Тогда его можно обозначить как 2k
Заменим в уравнении ax 2 + bx + c = 0 коэффициент b на выражение 2k
Теперь вычислим дискриминант по ранее известной формуле:
Вынесем в получившемся выражении за скобки общий множитель 4
Что можно сказать о получившемся дискриминанте? При чётном втором коэффициенте он состоит из множителя 4 и выражения k 2 − ac .
В выражении 4(k 2 − ac) множитель 4 постоянен. Значит знак дискриминанта зависит от выражения k 2 − ac . Если это выражение меньше нуля, то и D будет меньше нуля. Если это выражение больше нуля, то и D будет больше нуля. Если это выражение равно нулю, то и D будет равно нулю.
То есть выражение k 2 − ac это различитель — дискриминант. Такой дискриминант принято обозначать буквой D1
Теперь посмотрим как выводятся формулы и .
В нашем уравнении ax 2 + bx + c = 0 коэффициент b заменён на выражение 2k . Воспользуемся стандартными формулами для вычисления корней. То есть формулами и . Только вместо b будем подставлять 2k . Также на забываем, что D у нас равно выражению 4(k 2 − ac)
Но ранее было сказано, что выражение k 2 − ac обозначается через D1 . Тогда в наших преобразованиях следует сделать и эту замену:
Теперь вычислим квадратный корень, расположенный в числителе. Это квадратный корень из произведения — он равен произведению корней. Остальное перепишем без изменений:
Теперь в получившемся выражении вынесем за скобки общий множитель 2
Сократим получившуюся дробь на 2
Аналогично вывóдится формула для вычисления второго корня:
Видео:Формула корней квадратного уравнения с четным вторым коэффициентомСкачать
Какие формулы используют для нахождения корней квадратного уравнения при четном 2 коэффициенте
Для уравнений вида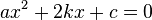 
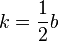
, то есть при чётном 
, где 
вместо формулы (1) для нахождения корней можно использовать эквивалентное выражение
Действительно, подставим в вышеприведённую универсальную формулу (1) корней уравнения указанное соотношение:
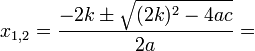
Для приведённого квадратного уравнения эта формула принимает вид:
.
Также при чётном удобнее вычислять значение не целого дискриминанта, а его четверти:
или, если уравнение приведённое:
.
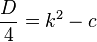
Все необходимые свойства при этом сохраняются:
0 Rightarrow D>0″ src=»http://upload.wikimedia.org/math/6/8/e/68eda98d8feacc2fbb9ee7adae1dc95b.png» />
(вместо знака «больше» в выражение может быть подставлены и другие знаки: «меньше» или «равно»). Подобным преобразованиям можно подвергнуть формулу для нахождения единственного корня при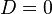 
:
.
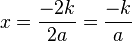
Обратите внимание, что для приведённого уравнения можно упростить расчёт следующим образом:
.
Отсюда следует важное и полезное правило: корнем приведённого уравнения с чётным вторым коэффициентом и равным нулю дискриминантом является половина второго коэффициента.
Эти выражения является более удобным для практических вычислений при чётном .
Видео:Квадратные уравнения (второй коэфф. чётный). Урок для ЕгораСкачать
Вывод формулы корней полного квадратного уравнения. Решение приведенных квадратных уравнений и уравнений с четным вторым коэффициентом
Разделы: Математика
Устный счет:
1. При каком значении Х , выражение принимает минимальное значение
а) 
; б) 
2. Зависимость y(x) выражается формулой y = 13x + 1 выразить x(y)
3. Не решая уравнения, определить, равносильны ли они:
4. Выделить полный квадрат: 
5. Вычислить пары чисел , удовлетворяющих условиям
| а) m + n = 4 mn = 4 | б) m + n = –3 mn = –18 |
- Какое уравнение называется полным?
- Что такое корни квадратного уравнения?
- Сколько корней может иметь квадратное уравнение?
Теорема. Квадратное уравнение не может иметь более двух различных корней.
Доказательство:
Предположим, что уравнение три различных корня: 
Если уравнение имеет корень, то после подстановки его в уравнение получится верное числовое равенство:
(1)
(2)
(3)
из (2) отнимаем (1)
–
_____________________
В каком случае произведение равно 0?
Так как 
= > 
0 = > a
+ b = 0. (4)
–
_________________
= > a
+ b = 0 (5)
– 
________________ 
а0 = > 
= > 
,
а по условию пришли к противоречию.
Давайте решим уравнение:
Самостоятельно:
a) 
Вместе:
б) 
Нравится ли этот способ? Нет! Тогда будем рассуждать иначе:
(формулу для нахождения корней квадратного уравнения учить проговаривать словами).
– дискриминант квадратного уравнения.
По теореме, доказанной нами , уравнение не может иметь более двух корней.
Количество корней зависит от D.
1). D > 0 
2). D = 0 
💡 Видео
Решаем квадратные уравнения, как?.. Чётный второй коэффициент нам в помощь.Скачать
Решение квадратных уравнений. Дискриминант. 8 класс.Скачать
Метод чётного коэффициента. #егэ2022 #егэ #математика #уравнение #beeschoolСкачать
Квадратные уравнения с четным вторым коэффициентомСкачать
Теорема Виета. 8 класс.Скачать
Квадратное уравнение: пример использования формулы для случая четного второго коэффициентаСкачать
Упрощенная формула корней квадратного уравнения. ЕГЭ и ОГЭ 2022 по математикеСкачать
5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать
Квадратное уравнение с четным вторым коэффициентом (D1)Скачать
Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать
решение квадратного уравнения ,когда второй коэффициент является четным числомСкачать
Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать
ФОРМУЛА КОРНЕЙ КВАДРАТНОГО УРАВНЕНИЯ. §20 алгебра 8 классСкачать
Квадратное уравнение с чётным вторым коэффициентомСкачать
Решение квадратного уравнения с выводом формулы корнейСкачать
Как решать квадратные уравнения без дискриминантаСкачать
