Какая зависимость выражается уравнением нернста поясните смысл входящих в него величин (4 видео)

Уравнение Нернста

Величина электродного потенциала зависит от природы металла, активности электролита и температуры. Эта зависимость описывается уравнением Нернста:

где Е° — стандартный электродный потенциал, В; R — универсальная газовая постоянная, равная 8,31 Дж/град • моль; Т — абсолютная температура, К; п — число электронов, участвующих в электрохимической реакции; F — постоянная Фарадея, равная 96500 Кл/моль; а — активная концентрация ионов металла в растворе, моль/л.

Если в уравнении (9.3) подставить числовые значения R, F, стандартное значение Т (298 К) и перевести натуральный логарифм в десятичный, получим

При низкой концентрации ионов электролита в растворе вместо активности можно использовать аналитическое значение концентрации ионов:

Зависимость потенциала водородного электрода от концентрации ионов Н + в растворе описывается уравнением

При повышении pH раствора потенциал водородного электрода смещается от нуля к отрицательным значениям. Поскольку потенциал водородного электрода является линейной функцией pH, его можно использовать для измерения pH.

Содержание

Напишите уравнение Нернста и укажите каково его значение
Применение уравнения Нернста в решении задач.
Пример 1:
Решение:
Пример 2:
Решение:
📸 Видео

Видео:Уравнение Нернста. Задачи на расчет потенциалов. Продукты в ОВР. Ч.5-2.Скачать

Напишите уравнение Нернста и укажите каково его значение

где Е — потенциал;

R — универсальная газовая постоянная, т.е кинетическая энергия 1 моля ионов при абсолютной температуре, равной 1о по Кельвину;

Т — абсолютная температура; n — валентность иона;

F — число Фарадея (заряд 1 моля одновалентных ионов);

Cнар. — концентрация ионов снаружи мембраны;

Свн. — концентрация ионов внутри клетки.

Уравнение Нернста — уравнение, связывающее окислительно-восстановительный потенциал системы с активностями веществ, входящих в электрохимическое уравнение, и стандартными электродными потенциалами окислительно-восстановительных пар.

Нернст изучал поведение электролитов при пропускании электрического тока и открыл закон. Закон устанавливает зависимость между электродвижущей силой ( разностью потенциалов ) и ионной концентрацией. Уравнение Нернста позволяет предсказать максимальный рабочий потенциал, который может быть получен в результате электрохимического взаимодействия, когда известны давление и температура. Таким образом, этот закон связывает термодинамику с электрохимической теорией в области решения проблем, касающихся сильно разбавленных растворов. E=E0+RTnFlnaOxaRed,

· E — электродный потенциал, E0 — стандартный электродный потенциал, измеряется в вольтах;

· R — универсальная газовая постоянная, равная 8.31 Дж/(моль·K);

· T — абсолютная температура;

· F — постоянная Фарадея, равная 96485,35 Кл·моль −1 ;

· n — число молей электронов, участвующих в процессе;

· aOx и aRed — активности соответственно окисленной и восстановленной форм вещества, участвующего в полуреакции.

Если в формулу Нернста подставить числовые значения констант R и F и перейти от натуральных логарифмов к десятичным, то при T=298K получим

Опишите механизм возникновения потенциала действия.

Следовая гиперполяризация
Потенциал-зависимые натриевые каналы

Фазы потенциала действия

1. Предспайк — процесс медленной деполяризации мембраны до критического уровня деполяризации (местное возбуждение, локальный ответ).

2. Пиковый потенциал, или спайк, состоящий из восходящей части (деполяризация мембраны) и нисходящей части (реполяризация мембраны).

3. Отрицательный следовой потенциал — от критического уровня деполяризации до исходного уровня поляризации мембраны (следовая деполяризация).

4. Положительный следовой потенциал — увеличение мембранного потенциала и постепенное возвращение его к исходной величине (следовая гиперполяризация).

Фазы

ЛО- локальный ответ

МПП-мембранный потенциал

13. что такое деполяризация и каковы ее механизмы?

Уменьшение МП относительно его нормального уровня (ПП) называют деполяризацией

Фаза деполяризации. Развитие ПД возможно только при действии раздражителей, которые вызывают деполяризацию клеточной мембраны. При деполяризации клеточной мембраны до критического уровня деполяризации (КУД) происходит лавинообразное открытие потенциалчувствительных Na+-каналов. Положительно заряженные ионы Na+ входят в клетку по градиенту концентрации (натриевый ток), в результате чего мембранный потенциал очень быстро уменьшается до 0, а затем приобретает положительное значение. Явление изменения знака мембранного потенциала называют реверсией заряда мембраны.

Рис. 2.4. Изменение мембран-ного потенциала, интенсивности калиевого и натриевого трансмембранного тока и возбудимости клетки в разные фазы потенциала действия.

Д – фаза деполяризации, Рб – фаза быстрой реполяризации, Рм – фаза медленной реполяризации, Г – фаза гиперполяризации;

Н – период нормальной возбудимости, Ра – период абсолютной рефрактерности, Ро – период относительной рефрактерности, Н+ – период супернормальной возбудимости, Н- – период субнормальной возбудимости

14. что такое порог деполяризации?

Порог деполяризации-это разность межу МП (Ео) и крити-ческим уровнем деполяризации (Ек):

Порог деполяризации является мерой возбудимости. Чем меньше порог деполяризации, тем меньшей силы необходимо при-ложить раздражитель чтобы вызвать развитие потенциала дейс-твия

15. в чем заключаются механизмы реполяризации?

фаза, во время которой восстанавливается исходный по тенциал покоя мембраны нервной клетки после прохождения через нее нервного импульса. Во время прохождения нервного импульса происходит временное изменение молекулярной структуры мембраны, в результате которого ионы могут свободно проходить через нее. Во время реполяризации ионы диффундируют в обратном направлении для восстановления прежнего электрического заряда мембраны, после чего нерв бывает готов к дальнейшей передаче через него импульсов.

Почему величина потенциала действия равна +40?

Это связано с тем, что та короткое время, в течение которого были от-крыты натриевые каналы и проницаемость мембраны была увеличенной со-здается, равновесный диффузионный натриевый потенциал.

Почему восстанавливается исходный мембранный потенциал после окончания потенциала действия?

Этот процессе состоит из 3 составляющих:

-инактивации натриевых каналов;

-увеличения проницаемости потенциал-зависимых калиевых кана-лов;

-работы натрий/калиевого насоса по восстановлению ионных гради-ентов.

Видео:Уравнение НернстаСкачать

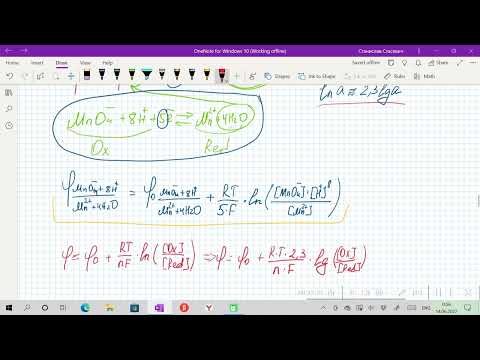
Применение уравнения Нернста в решении задач.

При рассмотрении вопроса об окислительно-восстановительных реакциях часто возникает необходимость расчета электродвижущей силы (ЭДС) и потенциалов отдельных полуреакций. В справочниках обычно приведены таблицы т.н. стандартных потенциалов тех или иных процессов, рассчитанных при р=1 атм, Т=298К и активностях участников равных 1. Однако в реальных задачах условия могут значительно отличаться от указанных выше. Как быть в таком случае? Ответ дает уравнение Нернста. В оригинальном виде оно выглядит так:

Как можно заметить, в уравнении фигурируют несколько постоянных величин. Также температура в подавляющем большинстве случаев равна 298К. Кроме того, можно заменить натуральный логарифм на десятичный. Это можно сделать путем умножения на коэффициент перевода. Если собрать все постоянные в единый множитель, то приходим к несколько иному, но более знакомому по учебным пособиям виду уравнения Нернста:

Такой вариант уравнения сильно облегчает жизнь в ряде случаев, например рассмотрении рН-зависимых процессов. Используя данное уравнение можно провести вычисления в любых условиях, приведенных в задаче. Рассмотрим характерные примеры задания по данной теме.

Пример 1:

Рассчитать ЭДС гальванического элемента, составленного из медной и цинковой пластин, погруженных в растворы 0.1М CuSO₄ и 0.01М ZnSO₄ соответственно. Коэффициенты активности ионов Cu 2+ и Zn 2+ принять равными единице.

Решение:

Для начала запишем уравнения протекающих процессов:

Далее находим по таблице стандартные потенциалы процессов:

Если в условиях задачи ничего не сказано про коэффициенты активности ионов, то можно считать их равными единице, как и в нашем случае. Тогда активности участников процессов можно принять равными их аналитическим концентрациям.

Найдем реальные потенциалы с учетом нестандартных активностей ионов:

Далее необходимо сравнить полученные величины между собой, чтобы определить, кто из участников процесса – окислитель. Потенциал меди больше, чем у цинка, поэтому она будет окислителем. Тогда найдем ЭДС системы:

Ответ: 1.13 В

Пример 2:

Одним из лабораторных способов получения хлора является действие KMnO₄ на концентрированную соляную кислоту. Можно ли провести процесс при рН=4?

Решение:

Для начала запишем уравнения протекающих процессов.

Далее находим по таблице стандартные потенциалы процессов:

Несложно заметить, что от рН в данном случае зависит только потенциал перманганата. Тогда воспользуемся уравнением Нернста и рассчитаем его реальный потенциал в условиях задачи: